基于Flexsim与遗传算法的混流组装线仿真与优化

杨 尚，施乃勇，侯 智

（重庆理工大学 机械工程学院，重庆 400054）

1913年亨利·福特建造了世界上第一条汽车流水组装线，福特汽车被大批量组装出来，产量大幅度提升。1995年，Nkasu等［1］提出了一种求解单模型装配线平衡问题的随机方法SALB，该方法能够在规划、设计和调度工作任务时，提供有价值的引导，但它仅仅是一种单模型求解方法。在实际生活中，装配线平衡涉及到生产的很多方面，是一种复杂的多目标规划问题，而遗传算法对于求解多目标、多模型等复杂寻优问题有很强的鲁棒性。2015年，Lorenzo［2］利用遗传算法对产线平衡进行寻优，取得了不错的成果。随着仿真技术的发展，2017年，Wang等［3］提出了一种基于遗传算法和系统仿真的组合优化方法，为研究装配线平衡问题提供了新的思路。

随着混流组装生产方式的快速发展，国内也进入了大规模的组装时代。为了提高组装效率，企业开始应用优化算法及仿真技术来解决产线平衡问题。2007年，黄克艰［4］针对混流生产，建立了一种基于遗传算法和Matlab的最小化工位闲置和超载时间的混流装配线调度模型，取得了显著成效。同年，赵建辉等［5］通过建模仿真得到生产线不同排产顺序的仿真结果，使得生产过程更加形象可控。遗传算法能很好解决产线平衡寻优问题，但也存在算法计算复杂、求解效率低等的缺点。2016年，张子凯等［6］针对遗传算法编码复杂的问题，提出一种基于多级随机分配编码的改进遗传算法，在降低计算复杂度的同时也能准确获得较优解。张洪亮等［7］提出一种基于最小化超载与闲置成本、最小化生产率变化成本的目标规划模型，优化了产线投产顺序，为解决产线平衡优化问题提供了新的思路。黄培星［8-9］基于这种模型对工时确定和不确定的U型混流装配线平衡问题展开研究，为混流生产找到了更细化的优化方案。郑谐等［10］、苗志鸿等［11］、马雪进等［12］通过分析混流装配线平衡改善及产品投放次序问题，对混流装配线平衡的改善作出了探析。

本文将以最小化闲置时间和过载时间为优化目标，提出一种结合矩阵编码及逆转变异方式的改进遗传算法，降低编码计算复杂度，提高最优解鲁棒性。并结合Flexsim仿真软件和改进遗产算法，分析Z企业发动机混流装配线平衡的实际案例，发现该优化方法有利于解决在制品堆积、工位超载、工位空闲等问题，也可以帮助企业解决订单无法按时交付的问题。

1 建立优化模型

1.1 问题描述

科学的混流生产就是在装配线上，多种产品按照一定的节奏、比例来进行生产。要达到装配线平衡，首先要制定合理的排产序列，品种、产量、工时、设备负荷等都是确定排产序列的重要指标。企业普遍存在混流产线不平衡的现象，主要包括3个原因：

1）在制品积压严重。这是由于部分后续工位加工时间过长，导致半成品在暂存区大量堆积。

2）设备阻塞。半成品堆积势必会造成后续工序的设备阻塞，影响产线的正常运转。

3）设备空闲。设备阻塞及设备空闲都会影响产线正常生产，降低产线效率，进而影响产品产量。

要解决上述问题，需要合理调整产品投产顺序，本文将以降低设备空闲率、平衡产线及提高产量为目标建立混流组装线优化模型。

1.2 模型建立

假设混流组装线上产品的型号数为M，在1个投产周期里，不同型号产品的需求分别为r1，r2，r3，…，rM，总需求量为设H（j，i）为R个产品的某一投产序列各工位（j＝1，2…N）组装不同产品（i＝1，2，…，N）所需的时间（j为组装线上的某个工位，Sj1＝0为第1个产品在该工位上装），H是一个各个工位操作时间矩阵。

由矩阵可知，产品在该工位上结束时间为Eji＝Sji+Tji。操作工人在第i个产品结束组装之后，将立刻返回到i+1个产品的组装的起点。整个组装序列中第i+1个产品加工起始点将会存在2种情况：

1）当一个工位的操作工人完成组装，这时该工位等待上一个工位的下一个产品的完成，即Eji小于等于Tj，i+1，这时造成该工位闲置等待，因此下一个型号的产品在该工位操作的起始时间为S（j，i+1）＝0。

2）工人未能按时在节拍内完成组装，即Eji大于或者等于K时，操作工人此时无法做其他活动，需继续完成该件产品的组装，由此可以看出下一个产品的组装起点为Eji-K（K为节拍时间）。

综上所述，S（j，i+1）＝max｛0，Eji-K｝在第1种情况下，混流组装线投产序列中第i个产品在第j个工位闲置时间为：Idleji＝max｛0，K-Eji｝。在第2种情况下，投产序列中第i个产品在第j个工位超载时间为：Overtji＝max｛0，Sji+Tji-K｝。

本文以最小化工位空闲时间与超载时间为目标，优化产品投产顺序，因此投产序的最优目标函数为：

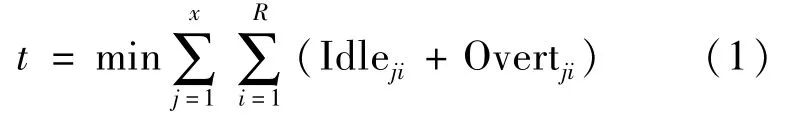
2 装配线案例

2.1 装配线现状

Z公司发动机组装线主要组装A、B、C、D 4种型号的发动机，每种型号包括8个组装步骤，分别是安装燃油供给机构、装点火系统、装排气系统、装进气系统、装调速机构、装飞轮风扇、装机油传感器、装曲轮连杆机构。发动机组装线上采用机器加工+人工辅助的组装模式，各工位设有暂存区，后道工序严格受前一道工序加工时间的约束，现有组装线整体布局为U型，如图1所示。

图1 组装线整体布局示意图

2.2 建立模型

该企业实行订单式组装，将产品月需求量平均分配到每天的加工任务之中。经过订单数据采集可以得到每月平均需求量、产品需求比重以及日需要量，A、B、C、D 4种发动机的日需要产量分别为55、100、155、100，日需要总产量为410台，投产比例为1∶2∶3∶2。如图2所示，组装线以ABBCCCDD的投产方式进行投产，Sji是第j个工位组装第i个产品的起始时间，Eji为第j个工位第i个产品组装结束时间。

图2 组装线组装情况示意图

工厂实行8 h上班制，即每天的工作时间为28 800 s，混流组装线的平均节拍K＝日工作时间／日需要总产量＝28 800 s／420台＝69 s，即在仿真模型中，2台发动机投产的时间间隔为69 s。使用秒表对工厂组装线上各工位测时，并利用Minitab进行数据拟合［13］，得到如表1所示的各工位标准时间，结合表1建立如图3所示的混流装配线的仿真模型。

表1 工位标准时间 s

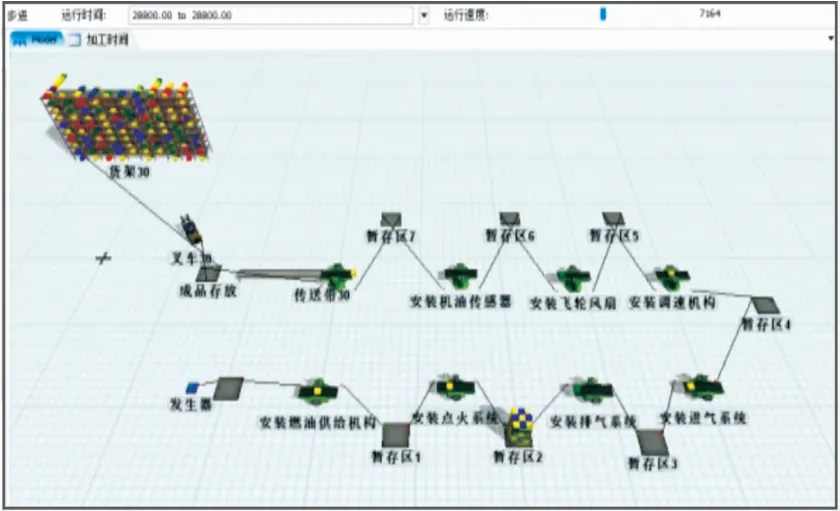
图3 Flexsim仿真示意图

2.3 问题描述

利用Flexsim软件建立仿真模型，得到了装配线生产的仿真结果，如表2、表3所示。分析仿真结果可以发现以下问题：① 暂存区2制品积压严重［14］，这是由于安装燃油供给机构耗时过长，导致半成品在暂存区大量堆积。②由表2可知，日产量仿真结果是368台，而日需求产量是410台，无法满足订单要求。从各工位的空闲率可以看出，安装进气系统工位空闲率高达38.90%，且其他工位空闲率也偏高，组装线总空闲时间为46 944.11 s，总体平衡率较差。③ 由表3可知，安装燃油供给机构、点火系统时，有较长的阻塞时间，分别为146、181 s，占阻塞总时长的90.15%。针对以上问题，下文将利用遗传算法对该混流线的投产顺序进行寻优。

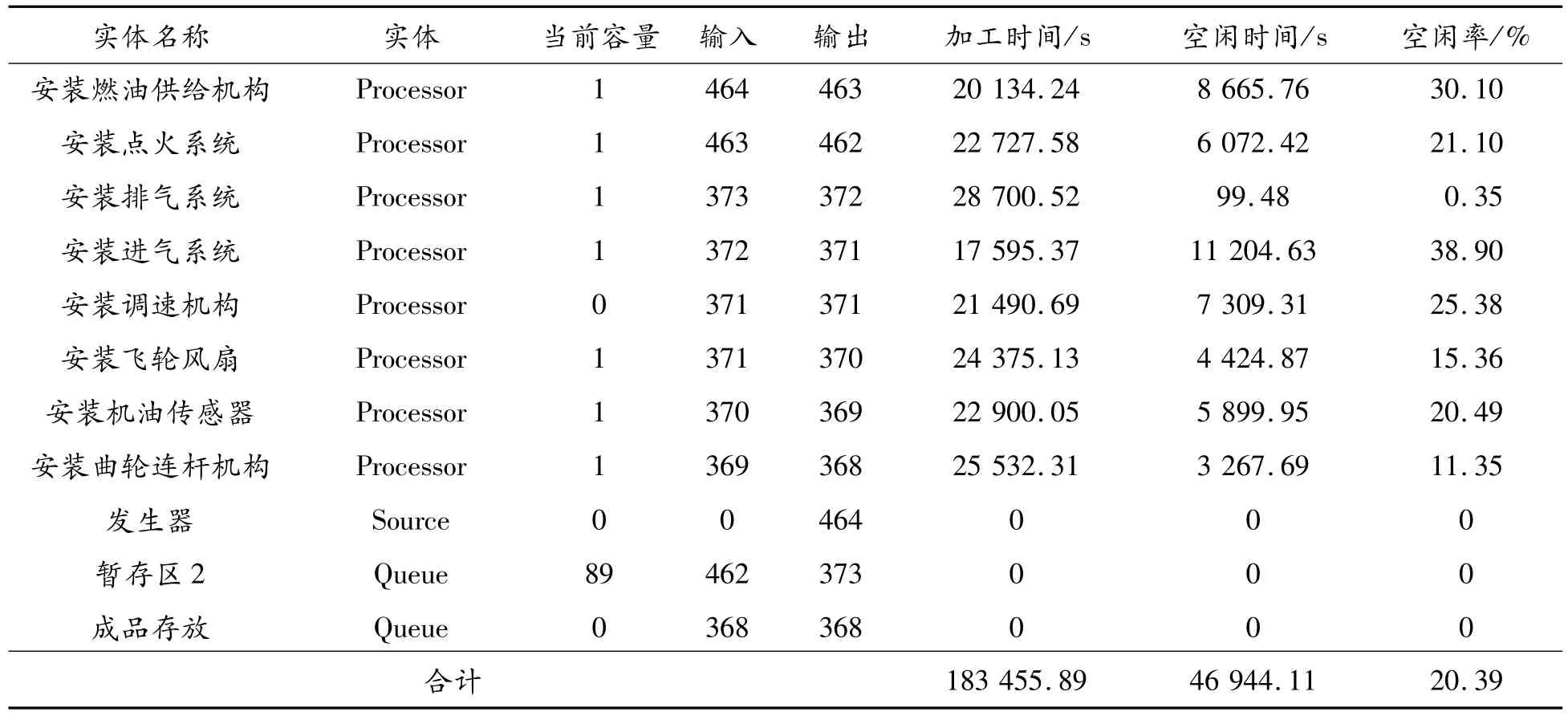
表2 仿真数据

表3 最小循环周期仿真结果

3 遗传算法优化

结合矩阵H，采用N×R的矩阵A来进行矩阵实数编码，区别于一般遗传算法常用的二进制编码方法，矩阵编码可有效解决算法运算过程中编码过长或编码、解码复杂的问题。在矩阵A中，每一行代表一个加工工位，每一列代表一个加工产品，矩阵中的生产单元代表在该投产序列中，第i（i＝1，2，…，R）个产品在第j（j＝1，2，…，R）个组装工位生产。

初始种群按行产生，R个产品（包含M个型号的产品）按照比例进行投产，每一个产品从最后一个工位随机产生加工时间，接着进行倒数第二道工序，不进行该道工序则不进入该工位，加工时间分配计入0，依次完成时间分配。初始种群产生的目标值记为最优目标值，按照上述步骤产生新的个体，比较不同种群的目标值可找到可行解。

交叉操作使用顺序交叉，变异操作选择逆转变异。

在该数学模型中，各工位空闲时间和阻塞时间之和为t，则适应度函数为：

基于适应度值，采用轮盘赌的方式为交叉、变异操作选择候选的染色体，适应度值越大，相应的被选择的概率就越大。假设种群大小为N，f（xi）为个体适应度值，则个体的选择概率公式为：

模型中采用Z企业发动机混合流水线的生产数据，算法的运行环境为Win 10操作系统下的Matlab 2015平台，相关参数设置如表4所示。

表4 参数设置

经过Matlab运行迭代50次后，适应度函数值随迭代次数的变化如图4所示，进化至35代时，算法渐渐收敛于最优解。输出的最优解个体为32 413 324，则解码得到的组装线最佳投产序列为CBDACCBD，该种投产方式下最小循环周期内各工位超载时间、空闲时间之和为2 650.6 s。

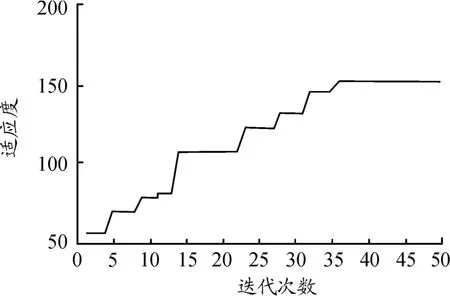
图4 适应度函数值变化曲线

4 效果评价

4.1 测试结果与分析

为了验证该改进遗传算法的性能，在硬件环境为Matlab 2015，IntelRRCore（TM）i5-5200U CPU＠2.20Hz，Windows 10下使用benchmark函数将改进遗传算法与文献［15］和文献［16］算法进行对比。

设定2种算法种群规模都为8，迭代次数为200次，采用Sphere、Rosenbrock和Griewank函数对该遗传算法进行性能测试，函数表达式如下：

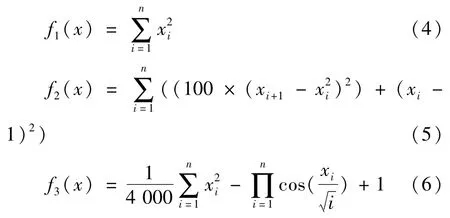
对每个函数，分别在不同维数条件下进行实验，实验结果见表5。对于Sphere和Rosenbrock函数，从实验结果可以看出改进遗传算法的最优解平均值更接近最优解，精度更高，其算法平均性能也比文献［15］、文献［16］算法更加稳定。对于Griwank函数，无论维数高低，改进遗传算法的平均性能也都优于其他算法。该算法通过矩阵编码和提高逆转变异概率可提高算法的局部搜索能力和求解精度，在求解后期，可加速最优解收敛且保持解的多样性和稳定性。

表5 算法测试数据

4.2 仿真结果与分析

优化投产序列后，对比改善前后图2与图5的Flexsim仿真图，可以看到暂存区在制品堆积明显减少。对比表2与表6的暂存区在制品堆积数，改善前为89，改善后为42，减少了47件，在制品堆积率减少了53%。在表2与表6中，对比成品存放数，改善前的日产量为368件，改善后为421件，该企业单日订单需求为410件，日产量提高了53件。各工位空闲率也明显降低，安装燃油供给机构的工位空闲率由30.10%下降到19.69%，降低了10.41%。安装飞轮风扇的工位空闲率由15.36%下降到2.81%，降低了12.55%。安装机油传感器的工位空闲率由20.49%下降到9.88%，降低了10.61%。对比表3与表7，优化投产顺序后，各工位空闲时间、工位阻塞时间之和由原来的2 801 s减少到2 650.31 s，减少了150.69 s。

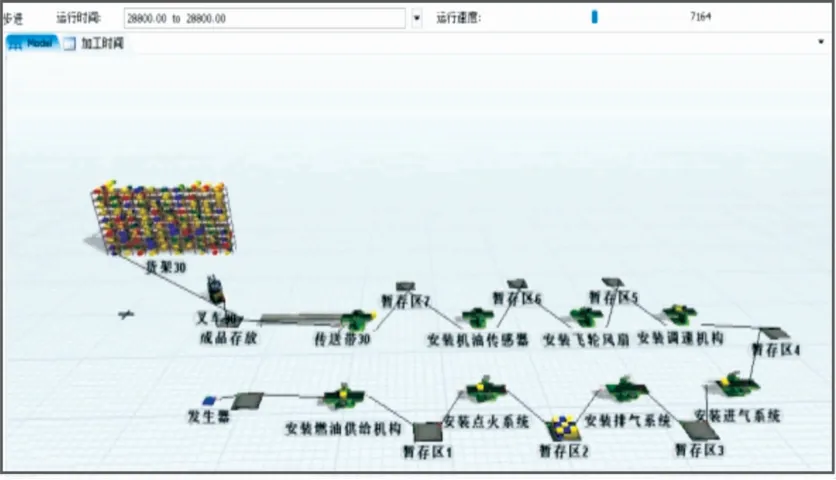
图5 Flexsim优化仿真示意图

混流装配线整体设备空闲率降低5.4%，产线空闲率由20.39%下降到11.88%，降低了8.51%，订单交付率提高了12.6%。解决了装配线的产线不平衡问题，使得产品投产转换更加合理，工序衔接更加流畅。

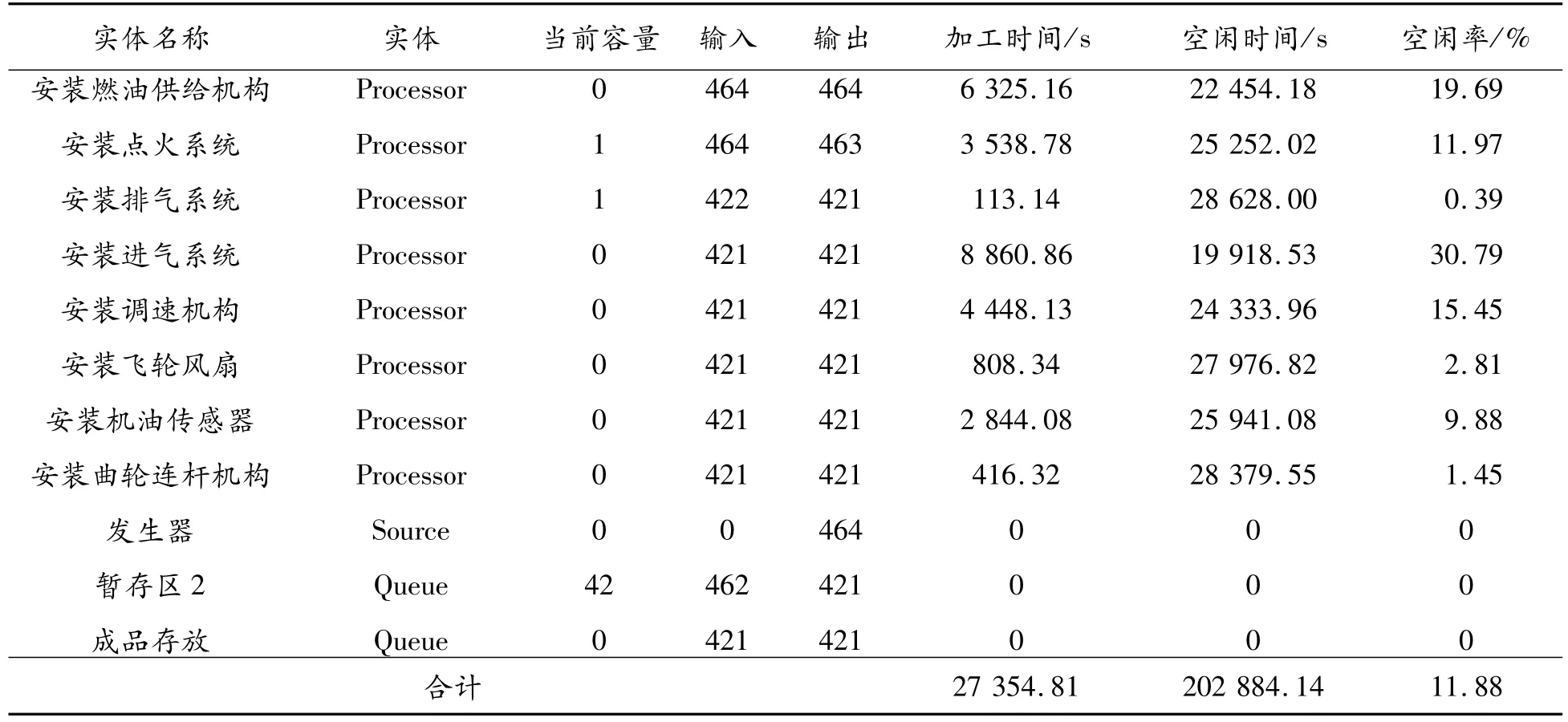
表6 改善后仿真结果输出数据

表7 改善后最小循环周期工位输出数据

5 结论

运用Flexsim软件建立三维可视化仿真模型，以Z企业发动机组装线为例进行仿真优化，使用矩阵实数编码改进遗传算法，解决了编码过长及编码、解码复杂的问题，采用逆转变异算子使解码结果简洁明了，更接近最优解，提高了寻优效率，有效地解决了企业的产线不平衡问题，达到了平衡工位负荷、提高组装线柔性及组装效率、降低组装成本的目的。