基于卷积神经网络的铁路曲线特征点检测算法

余宁 魏世斌 李颖 侯智雄

（1.中国铁道科学研究院研究生部，北京 100081；2.中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081）

铁路线路的曲线段结构特殊，容易发生轨道病害，而且危害较大，是轨道的薄弱环节。曲线段的线路状态不仅关系到列车实际运行的最高速度［1］，还直接影响乘车舒适性和车辆运行安全性［2］。只有对曲线参数进行准确的检测，及时发现病害，才能进行有效的养护维修，保持曲线区段线路的良好状态。曲线参数包括曲线长度、曲线正矢、轨距加宽、超高设置以及曲线上的轨道不平顺等，准确定位曲线特征点是精确检测曲线参数的基础。

我国自主研发的轨道检测系统中，曲线特征点检测算法是基于曲率和曲率变化率实现的［3］。由于实际线路中曲线半径范围过大，在普速铁路上识别较好的参数在高速铁路上容易发生漏检的情况，在高速铁路上检测效果较好的参数在普速铁路上容易发生误检的情况。即使识别出了曲线特征点，往往也会由于某些阈值设置不当而出现检测位置和实际位置偏差较大的问题。

本文结合当下流行的机器学习算法，提出一种全新的基于卷积神经网络的曲线特征点检测方法。该方法识别准确率高，同时适用于高速铁路和普速铁路的曲线特征点检测。

1 曲线特征点

从平面位置来看，轨道由直线段和曲线段组成。曲线段由两段曲率逐渐变化的缓和曲线和一段曲率恒定的圆曲线组成，如图1 所示。曲线段上钢轨外轨顶面应高于内轨顶面，形成一定的高度差（超高），以使得车体重力的分力抵消其离心力。缓和曲线段的作用是使得直线段到圆曲线段的曲率和超高连续变化，提高乘车舒适性［4-5］。

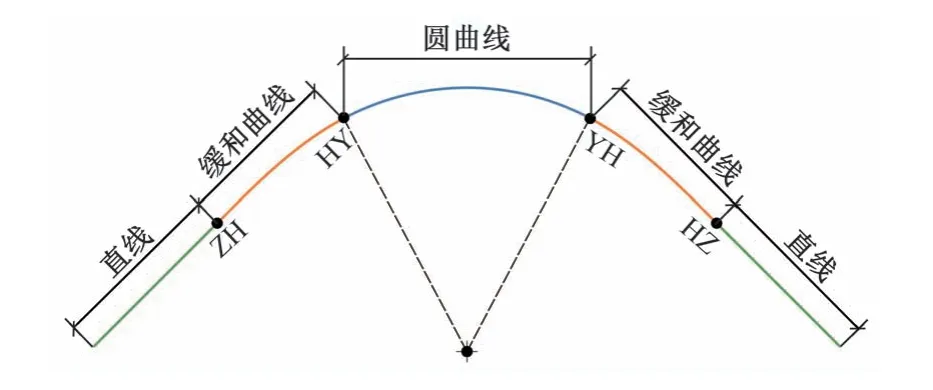
图1 曲线段的组成及曲线特征点

曲线特征点有4个，分别是：直线与缓和曲线的交点（ZH）、缓和曲线与圆曲线的交点（HY）、圆曲线与缓和曲线的交点（YH）、缓和曲线与直线的交点（HZ）。

2 卷积神经网络

卷积神经网络（Convolutional Neural Networks，CNN）在计算机视觉任务中运用广泛，与传统BP（Back Propagation）神经网络相比，具有局部连接、权值共享和下采样三大特性［6］。局部连接即卷积层的节点仅和上一层的部分节点相连，只用来提取局部特征。权值共享是指一个卷积核会对输入数据的不同区域做卷积计算来检测相同的特征，不同的卷积核参数不同，CNN 通过训练多个卷积核来提取不同的特征，从而可以大大减少网络参数的数量。下采样是指可以在保留有用信息的同时大幅度降低数据维度，从而降低网络复杂度，使网络具有更高的鲁棒性，同时又能有效防止过拟合。由于这三大特性，CNN 很适合处理缩放、平移和其他扭曲形式的输入数据，在计算机视觉任务中，可以直接以原始图片作为输入，无须进行复杂的预处理工作。

3 基于卷积神经网络的曲线特征点检测

曲线特征点检测包含两个任务，即需要得到一段曲线中的特征点类别及其位置信息，分别对应机器学习中的分类任务和回归任务。超高和曲率均能反映出曲线处的4 个特征点，故可以用超高或者曲率的数据作为CNN 的输入。对于计算机视觉任务而言，CNN的输入数据通常是一张彩色图片，包含三个维度，即图片的宽、高及RGB 颜色通道（RGB 即光学三原色，Red，Green，Blue），而卷积核通常是二维的。将CNN应用到曲线特征点检测任务中，其输入数据是一维的超高或者曲率数据，卷积核也是一维的。CNN 输入数据的维度通常是固定不变的，实际线路中曲线长度差异较大，故难以一次找到曲线的4 个特征点。最好的办法是选择一段合适长度的数据，使其中只包含4 个特征点中的1 个，然后通过CNN 计算得到特征点的类别及其相对位置。由于CNN 适合处理平移之后的数据，可以不用对全线的数据逐点计算，一次计算后可以跳过一定长度的数据进行下一次计算，这样可以很大程度上减少计算量。

4 训练集数据及分类类别

4.1 选取数据源

国内现役轨道检测系统中，超高是通过倾角计、滚动陀螺以及2 个垂向位移计得到的［7］，曲率是通过安装在车体的摇头陀螺得到的［3］。曲线段的超高和曲率检测结果如图2所示。

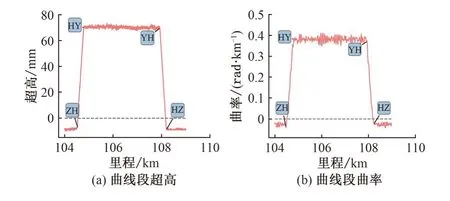
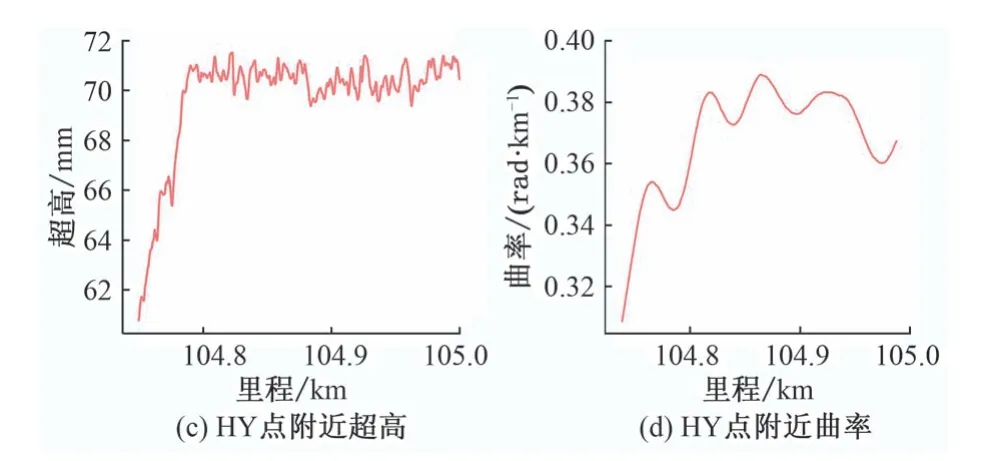
图2 曲线段的超高和曲率检测结果示例

由图2 可以看出，超高和曲率均能反映曲线的4 个特征点，但是超高在特征点处的转折更加明显，更有利于CNN 分类。因此，选择超高数据来检测曲线特征点。

4.2 选取数据段长度

国内现役轨道检测系统采取等空间间隔采样的方法采集传感器数据并进行合成计算，其空间采样间隔为0.25 m。选择连续Z个点的超高数据作为CNN的输入，Z的选择至关重要。Z过大会造成计算量大幅增加，且有可能在选择的数据段中包含多个特征点，对分类不利；Z过小，特征点处超高的局部变化规律容易和直线段受高频分量干扰的变化规律混淆，影响分类的准确性。

根据GB 50090—2006《铁路线路设计规范》［8］的表3.1.5 和TB 10621—2014《高速铁路设计规范》［9］的表5.2.5，缓和曲线段的最短长度不得小于20 m；根据GB 50090—2006 的表3.1.6 和TB 10621—2014 的式5.2.6-2，普速铁路中两缓和曲线段间的圆曲线和两相邻曲线段间的夹直线段长度不得小于30 m，高速铁路中不得小于48 m。因此，在50 m 范围内出现2 个及以上特征点的概率几乎为0。考虑一定的富余，最终选择40 m 长度的超高数据作为CNN 的输入，即Z=160。

4.3 数据归一化处理

神经网络对输入数据的尺度是比较敏感的，而实际线路的超高会因设计速度和曲线半径的不同而不同，因此须对输入数据做归一化处理，但又不能影响其在特征点处的变化规律。常用归一化处理方法有最大值归一化、最大值最小值归一化、反正切函数归一化、对数归一化等［10］。考虑到不能影响其在特征点处的变化规律，选择最大值最小值归一化的方法，计算公式为

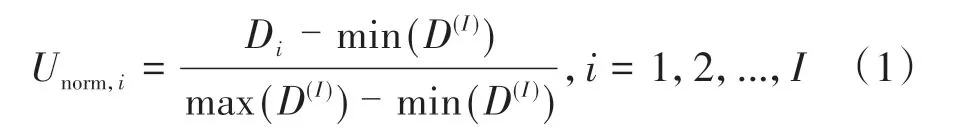
式中：Unorm，i为第i个原始数据归一化之后的结果；Di为第i个原始数据；D(I)为I个原始数据的集合；I为数据个数；max(D(I))，min(D(I))分别为集合D(I)的最大值和最小值。

4.4 超高数据分类

实际路线中由于曲线的方向变化，超高会出现正负交替的现象。圆曲线段的超高为正值称为左曲线，为负值称为右曲线。经最大值最小值归一化后，左右曲线在同一个特征点处的变化规律不同。若分类类别定义为4 种特征点类别，则要对超高数据取绝对值才能保证左右曲线在同一特征点处的变化规律相同。但是，对超高取绝对值会由于超高的零线偏移导致其在零线附近出现转折，破坏特征点处的变化规律，如图3所示。

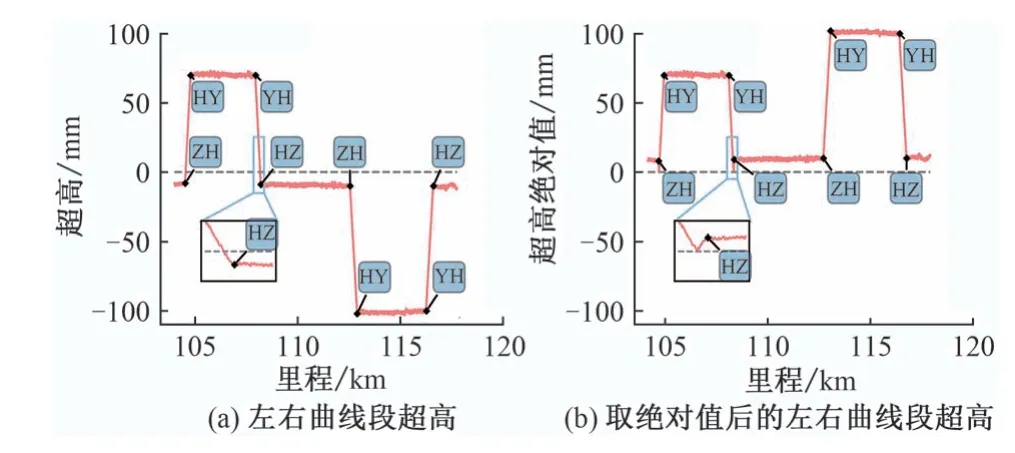
图3 取绝对值对超高变化规律的影响

由图3 可以看出，曲线特征点前后的一段数据包括倾斜向上（U），倾斜向下（D）和水平（H）3个类别，将其两两组合后有倾斜向上然后水平（UH）、倾斜向下然后水平（DH）、水平然后倾斜向上（HU）、水平然后倾斜向下（HD）4 个类别，共计7 个类别。同一类别对应于左右曲线不同特征点。以HU 类型为例，其分别对应于左曲线的ZH 点和右曲线的YH 点，ZH 点附近超高值绝对值较小，而YH 点附近超高值绝对值较大，故设置一个合适的阈值即可区分是左曲线的ZH 点还是右曲线的YH点。

4.5 训练集数据

一条训练数据中包括Z个点归一化处理后的超高数据、超高数据的类别及特征点相对位置。特征点相对位置即特征点相对于其所在的数据段中的位置除以Z。对于U，D，H 类别的超高数据，特征点相对位置为0。对于HU，HD，UH，UD 类别的超高数据，希望特征点的位置在中心位置附近，这样特征点处的变化规律更加明显，有利于提高分类准确率。实际制作训练集数据时，可以设置一个范围阈值（本文设为40）。确定特征点偏离中心位置超出此阈值的超高数据的类别时，根据其数据分布情况设为与U，D，H最接近的一种。7 种类别的超高数据经最大值最小值归一化后如图4所示。

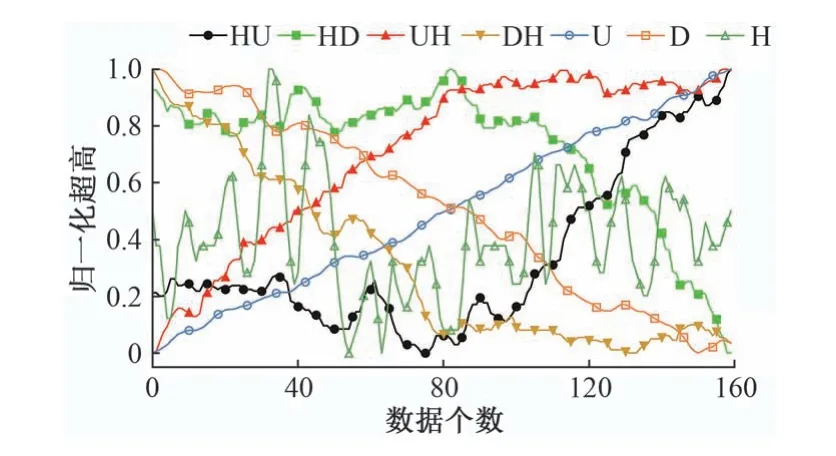
图4 归一化处理后的7种类别超高数据

5 网络结构

本文所使用的CNN 模型可视化网络结构如图5所示。采用了2 层卷积层（C1，C2）和2 层下采样层（S1，S2），而后紧跟1 层64 个神经元的全连接层（L1），最后2个全连接层中L2_1（7个神经元）用于分类，L2_2（1 个神经元）用于回归输出特征点的相对位置。使用RELU（Rectified Linear Units）激活函数，超高数据经过卷积核提取特征、下采样和非线性激活后，得到宽度为10、高度为1、深度为32 的特征数据，而后与全连接层连接。

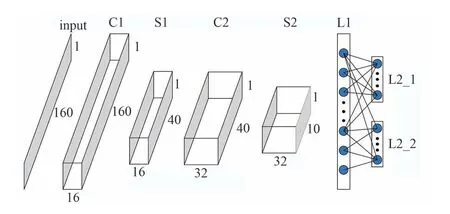
图5 CNN模型可视化网络结构

6 模型训练及预测

6.1 模型训练

6.1.1 训练集和测试集数据

根据京广（北京—广州）铁路（普速）、成贵（成都—贵阳）高速铁路和石太（石家庄—太原）高速铁路的超高原始检测数据，生成了约11万条数据，各类别的样本数据分布见表1。可以看出，各类别分布较均衡。从各类别的数据中随机抽取80%，作为训练集数据来训练模型，另外20%作为测试集数据来验证模型准确性。

表1 训练集样本分布

6.1.2 损失函数

损失函数（也称代价函数）即待优化的目标函数。对于多分类任务，CNN 输出对各类别的观测值，其值大小不确定。通常使用softmax 分类器［6］进行处理，将各类别的观测值转化为0～1的概率值，计算公式为

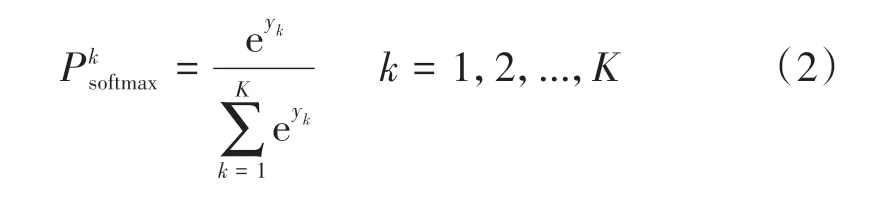
观测值经softmax 分类器处理后，使用交叉熵［6］计算预测概率分布和真实概率分布的差异作为损失函数。交叉熵起源于信息论，主要用于度量两个概率分布的差异，计算公式为

式中：J为交叉熵损失函数；n为样本编号；N为一次迭代的训练样本数量；yn为第n个样本的真实类别，取1到K之间的整数。

对于回归任务，最常用的损失函数为均方误差损失函数。均方误差［6］（Mean Squre Error，MSE）度量的是预测值和真实值差异的平方的均值，只考虑误差的平均大小而不考虑其正负。由于计算经过平方，会使得导致预测结果偏差较大的网络参数得到更多的调整。均方误差损失函数M的计算公式为

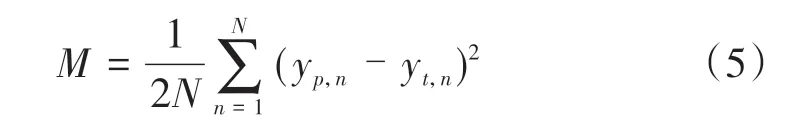
式中：yp，n，yt，n分别为第n个样本的预测值和真实值。

最终的目标是通过同一个网络实现对曲线特征点的分类及其相对位置的预测，分别对应交叉熵损失函数J和均方误差损失函数M。训练模型时有两种处理方法，可以对J和M赋予相应的权重后组合成一个损失函数，也可交替使用J和M。试验表明，在迭代相同次数后两种方法最终在测试集上的表现几乎没有差异，但第一种方法训练速度更快。本文采用第一种方法，组合成的损失函数L的计算公式为

6.1.3 训练结果

使用tensroflow 深度学习框架搭建并训练CNN 模型，每次迭代时随机从训练集中选取2048 条数据，迭代20万次后模型在测试集上的分类准确率达到99%，相对位置预测的平均偏差小于2%。训练过程中训练集的损失函数以及测试集的分类准确率和特征点相对位置均方误差见图6。

图6 训练结果

6.2 模型预测

模型训练完成后，使用京包高速铁路的超高数据进行预测。为了减少计算量，若某一数据段的预测分类结果为U，D，H 之一，则直接跳过40 个点进行下一次预测。为了提高预测结果的准确性，对于预测分类结果为HU，HD，UH，DH 之一的数据段，将CNN 预测的特征点相对位置加上数据段的起始位置得到初始中心点位置P，将P前后移动5个、10个点，得到4个中心位置P-10，P-5，P5，P10。以这5 个位置为中心从原始超高数据中取5 段数据，经归一化处理后用CNN 进行预测，得到5 份预测结果，用这5 次预测的类别对最终类别进行投票。若某一类别得票大于4，则认为找到了某个特征点F，特征点位置为5 次预测中预测类别与F一致的预测位置的平均值。京包高速铁路曲线特征点的预测结果如图7 所示。可以看出，模型能够相当准确地识别出曲线特征点并找到其位置。

图7 京包线曲线特征点检测结果

利用CNN 计算图7中5条曲线的特征点检测结果对应的曲线长度，并与现役轨道检测系统对此5 条曲线长度的检测结果进行对比，见表2。可以看出，CNN对曲线长度的检测结果与实际情况更加接近。因此，CNN对曲线特征点的定位更准确。

表2 现役轨道检测系统和CNN检测结果 m

7 结语

本文提出的基于卷积神经网络的曲线特征点检测算法具有准确率高，检测效果不受线路等级影响等优势。不足之处在于卷积神经网络计算量较大。本文在确保检测精度要求的基础上已经尽可能缩小了网络模型，但仍难以满足实时检测的要求。现有轨道检测系统运行在QNX（Quick UNIX）实时操作系统上，对算法实时性要求较高。若将卷积神经应用到检测系统当中，一种解决方案是对曲线特征点检测采取异步检测的方案，即不要求算法实时输出，由于检测时无需对每一段超高数据进行计算，因此仍能在检测车运行时间内得到最终结果；另一种解决方案是将曲线特征点识别算法迁移至轨道检测系统的后端服务器上，利用GPU（Graphic Processing Unit）加速其计算过程。本文只研究了该算法的理论可行性，关于如何将其应用到轨道检测系统上仍有很多工作要做。