基于AHP 的区域干旱等级综合评价及其应用

蒋 欣，常留红，杨思宇，王瀚锐，周 磊

（1.湖南省鑫誉项目管理有限责任公司，湖南 长沙 410000； 2.长沙理工大学水利工程学院，湖南 长沙410114； 3. 湖南省水利水电科学研究院，湖南 长沙 410007）

前 言

干旱作为最严重的气象灾害之一，影响范围广，持续时间长，后续和潜在损害大，已经对我国社会经济和人民生活造成严重影响。受全球气候变化和经济社会高速发展的影响，干旱呈现频次增加、范围扩大之势。目前，我国60%以上的县区为易旱地区，旱情重、影响程度深，治理点多面广，抗旱减灾任务艰巨繁重，所需资金较大，因此，必须按照轻重缓急、突出重点、效率优先的原则，进行分级治理。

国内外许多学者从气象干旱、农业干旱、水文干旱、社会经济干旱四个方面对干旱及干旱指标评定做了大量研究[1～2]。Palmer[3]提出了帕尔默干旱指标（PDSI），有效地反映了地区干旱程度及干旱时间尺度；Bhalme[4]提出区域旱涝指数（DAI/FAI），该指数有效说明了区域和年季尺度的水分状况。Palmer[5]在PSDI 指标的基础上，提出了应用于较大空间尺度上的作物水分指标（CMI），能够充分反应短期农作物的水分状况；孙荣强[6]通过水平衡干旱模拟模型，确定了综合考虑气候-土壤-植物体系和各时段旱象对整个作物旱情的影响程度的旱情评价体系；邱林[7]建立能准确反映干旱对农业造成损失的农业干旱评估指标的静态模型和动态模型。熊立华、任立良[8～10]引进了具有物理分布机制的分布式模型和水文干旱模型。Ohlsson[11]提出了概化干旱对社会影响的SWSI 指标。冯平[12]采用人工神经网络技术的方法，提出干旱程度的评估模型。冯利华[13]根据风级和震级的计算原理，提出了干旱等级和灾度的概念。

随着人类活动的不断加剧，区域干旱也表现出差异性、随机性、突发性、重现性以及无序性等复杂性的特点，加之干旱对社会影响的广泛性及自身的时空局限性，因此，单一的干旱评价指标难以有效反应干旱的内在机理及其影响程度，本文基于层次分析法，建立干旱影响指标体系，建立区域干旱等级综合评价模型，结合现行的分项旱灾评价标准，提出干旱等级综合评价标准。根据衡邵干旱走廊33 个县（市、区）1990-2010年的统计数据，将评价模型应用于33 个县（市、区），通过干旱等级分级，并对该区域内33 县（市、区）实施分级治理，为区域干旱分级综合治理提供科学依据。

1 AHP 评价原理

1）建立指标体系

干旱评价指标涉及领域较多，相互关系复杂，在选取综合评价指标时应遵从科学性、系统性、可比性、动态性和简明性原则，选取指标体系应具有明确的内涵，尽可能全面地反映干旱的特征，并考虑指标的可测性、规范性、一致性和实用性，尽可能具有较长期的数据资料，可进行不同时期比较研究。

2）判断矩阵

对从属于上一层某要素Ai的同层各个要素Bi进行两两比较，以要素Ai作为判断准则进行量化标度比较，构成判断矩阵B[B=（bij）n×n]。

判断矩阵中各个元素的数值一般采用1～9 位标度法确定，在相邻的2 个等级之间可依次用2、4、6、8 或其倒数将其量化，如表1 所示。

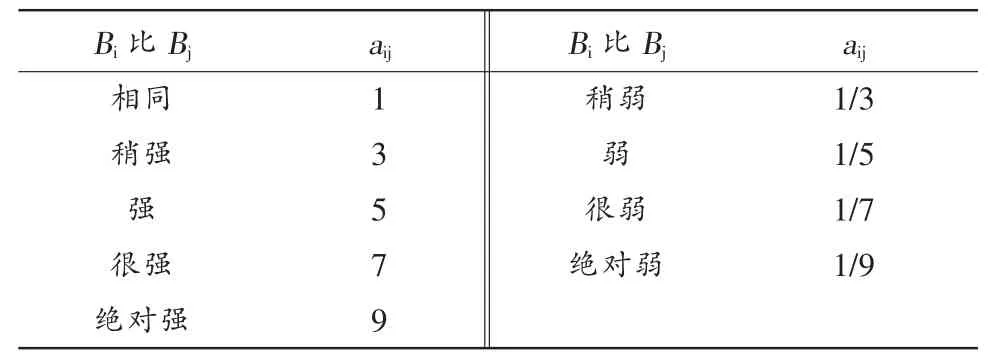
表1 判断矩阵取值

3）计算权向量

根据判断矩阵B 求出其最大特征特征值λmax和对应的特征向量W，特征向量W 经归一化后即为所求权向量，计算判断矩阵中与上一层某一因素有关的同一层次因素之间相对重要性的次序权值。

4）一致性检验

在实际应用中为避免其他因素对判断矩阵的干扰和保证判断矩阵满足大体一致性，需要进行一致性检验，符合一致性要求。判断矩阵一致性检验计算：

其中，CR 是一致性判断指标，当CR＜0.1 时，判断矩阵符合一致性要求，否则需要对判断矩阵进行调整；CI 是判断矩阵的一致性指标：

其中，λmax是判断矩阵的最大特征值，n 是成对因子比较的个数。

RI 为随机一致性指标，通过查表确定，如表2所示。

表2 随机一致性指标RI 值

2 区域干旱等级综合评价模型

2.1 评价指标体系

干旱评价指标涉及领域较多，相互关系复杂，本文结合各地区水资源条件、水利基础设施供水能力和经济社会发展实际需求的基础上，紧扣水资源与“三生”用水的主要矛盾及存在的突出问题，根据相关干旱等级评价标准，统筹各地区干旱特征，选取受灾人口百分比（受旱人口占总人口的百分比）、农作物受灾面积百分比（农业受旱面积占总耕地的百分比），缺水率（缺水量占总需水量）、经济损失百分比（受旱影响经济值占区域GDP 的百分比）、石漠化程度（石漠化面积占国土面积的比例）等5 项综合指标，建立区域旱情评价指标体系。区域干旱等级综合评价递阶层次模型，如图1 所示。

图1 区域干旱等级综合评价递阶层次模型

2.2 计算各项评价指标权重值

基于Dephi 专家调查法和1～9 位标度法，对同属于上一层某因素（A1）的同层各个因素（Bi）进行两两比较，并对其相对重要性赋予一定分值，从而构造出上下层次之间隶属关系的判断矩阵B[B=（bij）5×5]，如表1 所示，计算权向量W 采用和积法；判断矩阵见表3。

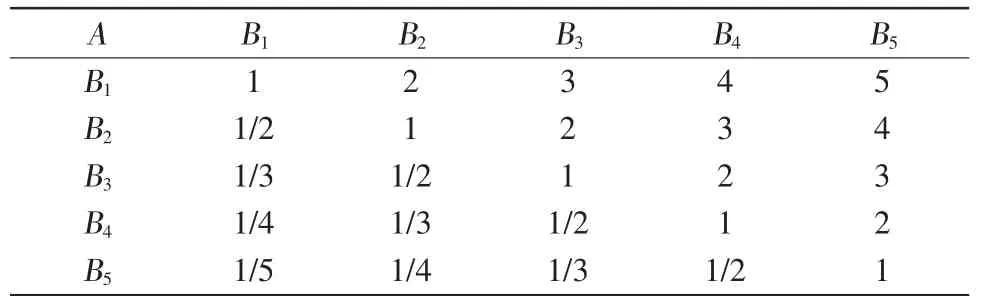
表3 判断矩阵A-B 数值表

对矩阵B 的每一列进行正规化，

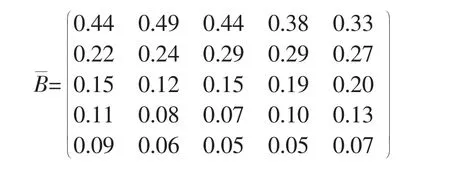
计算出正规化后的矩阵B 为：

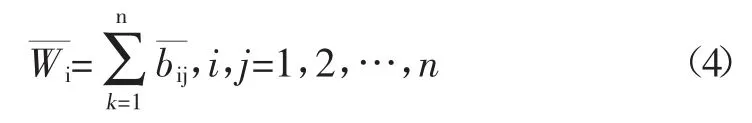
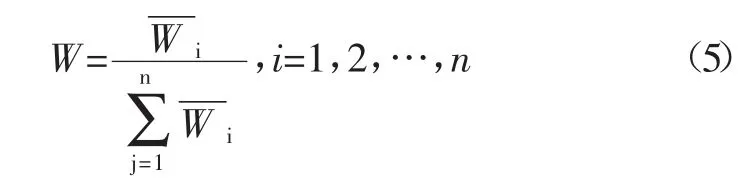
和积法中计算判断矩阵B 最大特征值λmax公式如下，

其中

由表2 可知随机一致性指标RI=1.12，根据式（1）、式（2）进行判断矩阵的一致性检验，得：CI=0.017 5，CR=0.015 6<0.1，判断矩阵符合一致性要求。见表4。

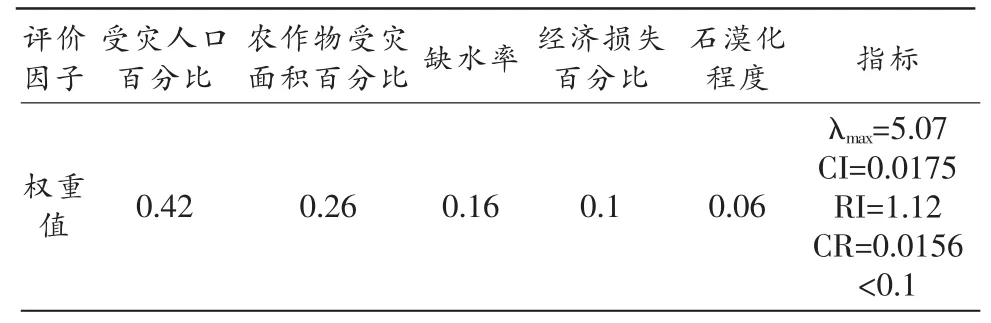
表4 区域干旱等级综合评价模型

3 衡邵干旱走廊干旱等级计算

基于衡邵干旱走廊1990—2010 年20 年的统计数据，将区域干旱等级综合评价模型应用于衡邵干旱走廊33 个县，对各县区的干旱情势进行综合评价。

干旱指数=人口百分比×0.42+农作物受旱面积百分比×0.26+缺水率×0.16+经济受旱百分比×0.10+石漠化程度百分比×0.06；干旱综合评价指数=某县区干旱指数/所有县区干旱指数之和；以衡阳县干旱综合评价指数计算为例，衡阳县干旱指数=11.61%×0.42+18.75%×0.26+6.57%×0.16+3.6%×0.10+2.74%×0.06=0.113。

衡阳县干旱综合评价指数=0.113/4.0921=0.0276。

同理，计算其他县（市、区）干旱综合评价指数计算结果，见表5。

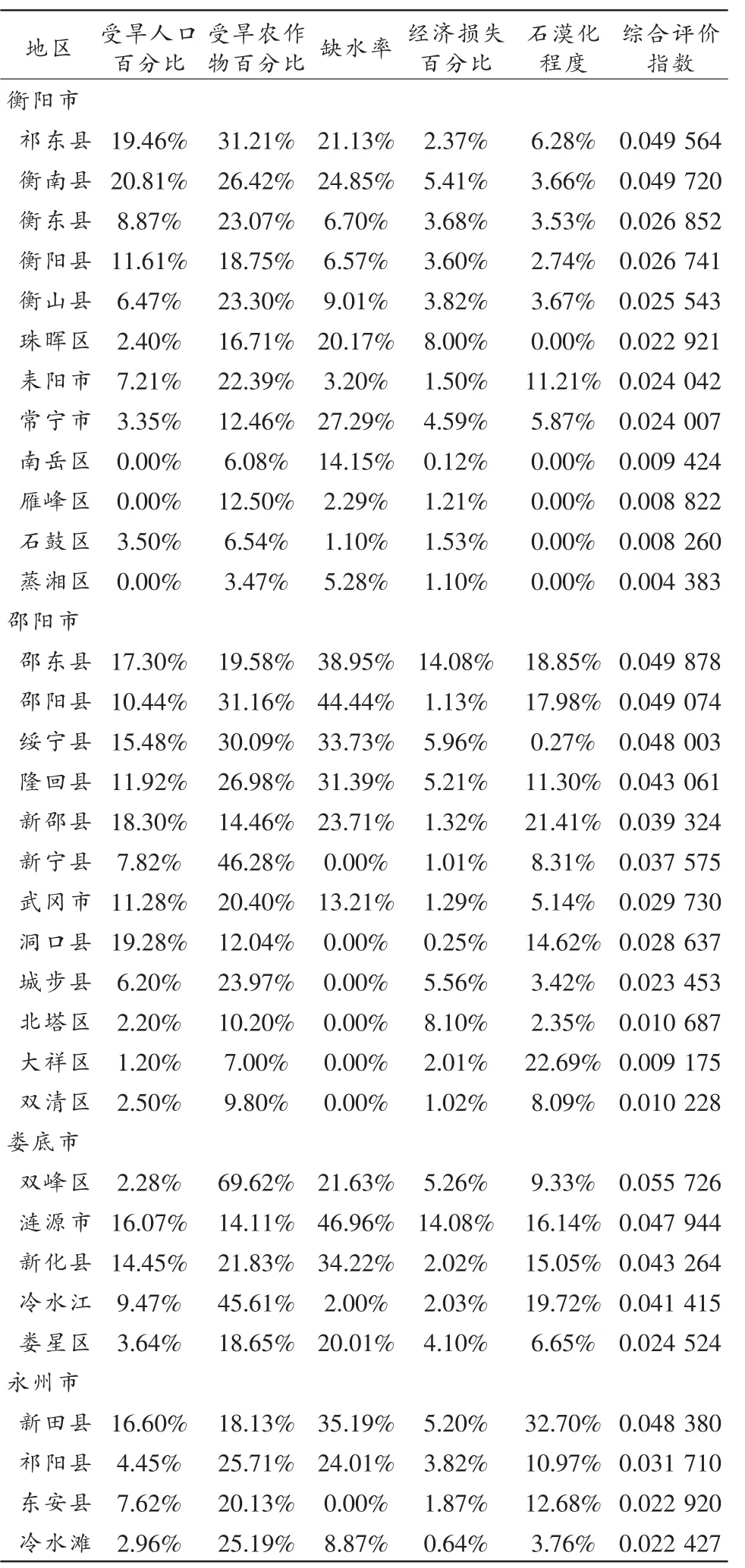
表5 衡邵干旱走廊干旱综合评价指数

根据《气象干旱等级》、《农业干旱等级》和《干旱灾害等级》国家标准，确定规划区干旱综合等级划分标准，将规划区分为严重干旱区、重度干旱区、中度干旱区和一般干旱区四个等级，见表6 和表7。

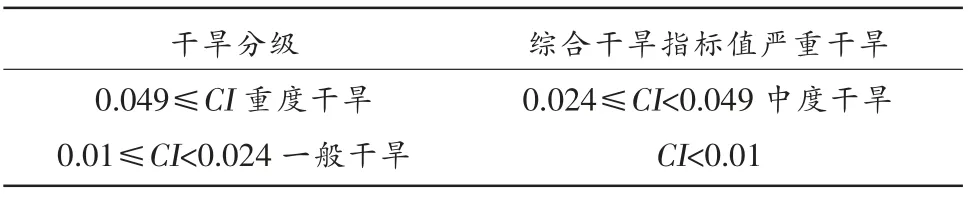
表6 衡邵干旱走廊综合治理等级标准

表7 衡邵干旱走廊综合治理等级区划表

4 结 语

1）基于层次分析法，在充分考虑干旱对社会影响的广泛性及自身的时空局限性的基础之上，建立了区域干旱等级综合评价模型，有效反应干旱的内在机理及其影响程度，并结合《气象干旱等级》、《农业干旱等级》和《干旱灾害等级》，提出干旱等级综合评价标准，对区域干旱进行干旱等级区划，实施分级治理，为区域干旱综合治理提供科学依据。

2）应用区域干旱等级综合评价模型及标准，对衡邵干旱走廊进行干旱综合等级评定，将衡邵干旱走廊的各县（市区）根据等级标准分级，为实施分级治理，有效降低特大干旱对区域的社会经济影响提供借鉴作用。本模型适用于在干旱治理点多面广、抗旱减灾任务艰巨繁重、所需资金较大的干旱区域推广应用。