复杂载荷下裂纹SIF计算的子模型技术
江 威,黄小平
(上海交通大学 海洋工程国家重点实验室,上海 200240)
0 引 言
疲劳强度校核一直是船舶结构强度中的重要组成部分,疲劳强度评估中,基于断裂力学方法的寿命预报能够考虑初始缺陷、载荷次序等因素的影响,是未来发展的趋势。但将基于断裂力学的寿命预报方法应用于工程实际结构时,对于重要参数SIF的求解仍存在问题[1]。目前较权威的SIF计算公式[2– 5]仅限于简单载荷和简单应力场,尚不能对工程实际结构进行推广,DNV规范推荐将子模型技术应用于复杂载荷下构件中裂纹SIF求解[6]。子模型技术是在整体分析模型基础上获取局部区域精确解的一种高级有限元分析技术,其中子模型是为分析结构细节(孔、角隅、裂纹、接触面等)而从原模型分割出的一部分区域[7]。通过求解原模型,子模型边界条件一般可由位移法(DBS)或应力法(SBS)得到[8],其中位移法因其离散误差收敛更快被广泛推荐使用[9–11],故子模型技术又称为“切割边界位移法”或“特定边界位移法”[12]。子模型技术基于圣维南原理,即实际分布载荷如果被等效载荷代替,应力和应变只会在施加载荷的位置发生变化[13–14],这表明应力集中效应只会发生在载荷施加部位。
基于Ansys内部的子模型分析技术具有以下优点[15]:
1)减少甚至取消了有限元模型中的复杂传递区域;
2)方便对局部区域进行细节分析并得到精确解;
3)可用于验证原模型的网格划分是否满足要求。
子模型分析过程一般包括建立和分析原整体模型、建立子模型、生成切割边界位移及分析子模型4个步骤,并有以下注意事项[7,16]:
1)子模型和原整体模型相应位置处的单元属性及位置需一致;
2)切割边界只能选在壳单元、体单元内或壳体单元连接处;
3)切割边界应远离应力集中区域;
4)原整体模型相应位置处网格有必要进行足够程度的细化。
基于船舶结构的特性及Patran对壳、梁单元的强大支持,行业内一般在Patran中建立全船有限元模型,此时若对相关疲劳热点进行断裂力学评估,需考虑结合Patran和Ansys两套软件的子模型技术,即通过在Ansys中建立与Patran原整体模型待评估位置对应的子模型进行分析,与单纯在Ansys内部实现边界切割和位移插值的子模型技术相比,除需满足基本操作要求,还有以下问题:
1)疲劳寿命评估中,对不同尺寸表面裂纹SIF求解需要使用三维单元[17–18],也就意味着Ansys子模型及原Patran壳模型的对应位置都要使用体单元建模,即删除原Patran整体模型对应位置处的壳单元,用体单元重建,并用MPC连接重建的体单元和其周围壳单元,方可保证壳体间变形正确传递;
2)对于结合Patran和Ansys的子模型技术的疲劳评估,若疲劳热点较多且位置各异,仅在Ansys APDL中往复调整子模型位置与原模型一致是不明智的,此时建立子模型应优先考虑方便裂纹建立的做法,然后在Ansys外部实现坐标转换。由此可见,这种子模型技术的前处理的实现难度较高,各环节的实现低效易出错。目前较少学者采用子模型技术进行裂纹扩展分析[7],也很少有人对有限元前处理过程进行有效优化[19],这在很大程度上限制了子模型技术在船舶疲劳强度校核中的推广。
本文提出“逐周分层法”、“转换矩阵法”及“映射划分法”,着眼于解决从Patran整体模型到Ansys子模型实现过程中壳体单元间MPC创建低效、不同坐标系间节点位置信息转换困难及裂纹自由划分局限性的问题,并基于VBA和APDL语言编写插件M PC_arranger_V 1.0,FEM_coo r_transfer_V 1.0及C rack_m apper_V 1.0进行实现。同时选取某B型LNG燃料舱关键疲劳节点,参考DNV及ABS相关规范[20],对子模型边界位移进行验证,并进行疲劳热点处裂纹的SIF计算。
1 子模型技术简介
基于断裂力学进行疲劳评估需要求解SIF,目前Ansys自带SIF求解命令KCALC,如图1所示。
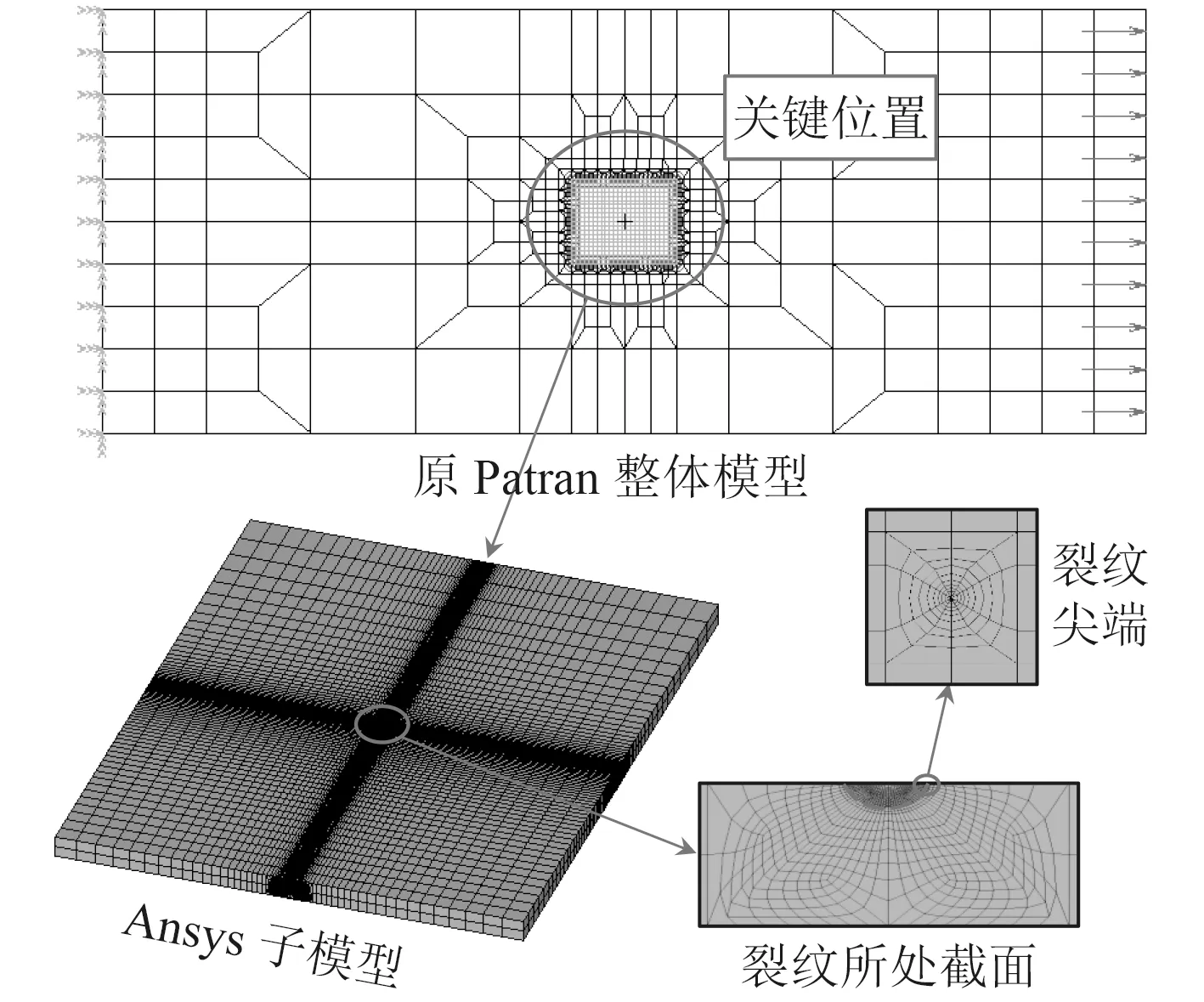
图 1 应力强度因子计算流程Fig. 1 The procedure of SIF calculation
针对一种结合Patran和Ansys的子模型技术[1],以承受简单拉伸载荷的平板为例介绍其实现流程:
1)在Patran中采用shell单元建立厚度为t的平板模型,对板左端施加六自由度约束,对板右端施加垂直于板厚方向的拉应力。对板中心区域网格进行t×t细化,细化区域不少于10t范围,为实现对三维表面裂纹SIF的求解,需将细化区域的板单元拉伸为实体单元,并在壳体边界使用RSSCON Surf-Vol型MPC关联对应节点自由度,然后提交计算。
2)在Ansys中建立与Patran体单元部分对应的子模型,并对裂纹进行网格划分。然后输出Patran中实体单元边界节点的位置信息,经坐标转换及插值施加为Ansys子模型的边界条件,即可实现SIF的求解。
2 壳体边界MPC的创建
如图2所示,Patran模型中体单元和壳单元的边界节点需要使用RSSCON Surf-Vol型MPC进行关联。此MPC需将上下层边界节点(即体单元边界节点)设为独立点,中间层边界点(即壳体联合边界节点)设为非独立点。
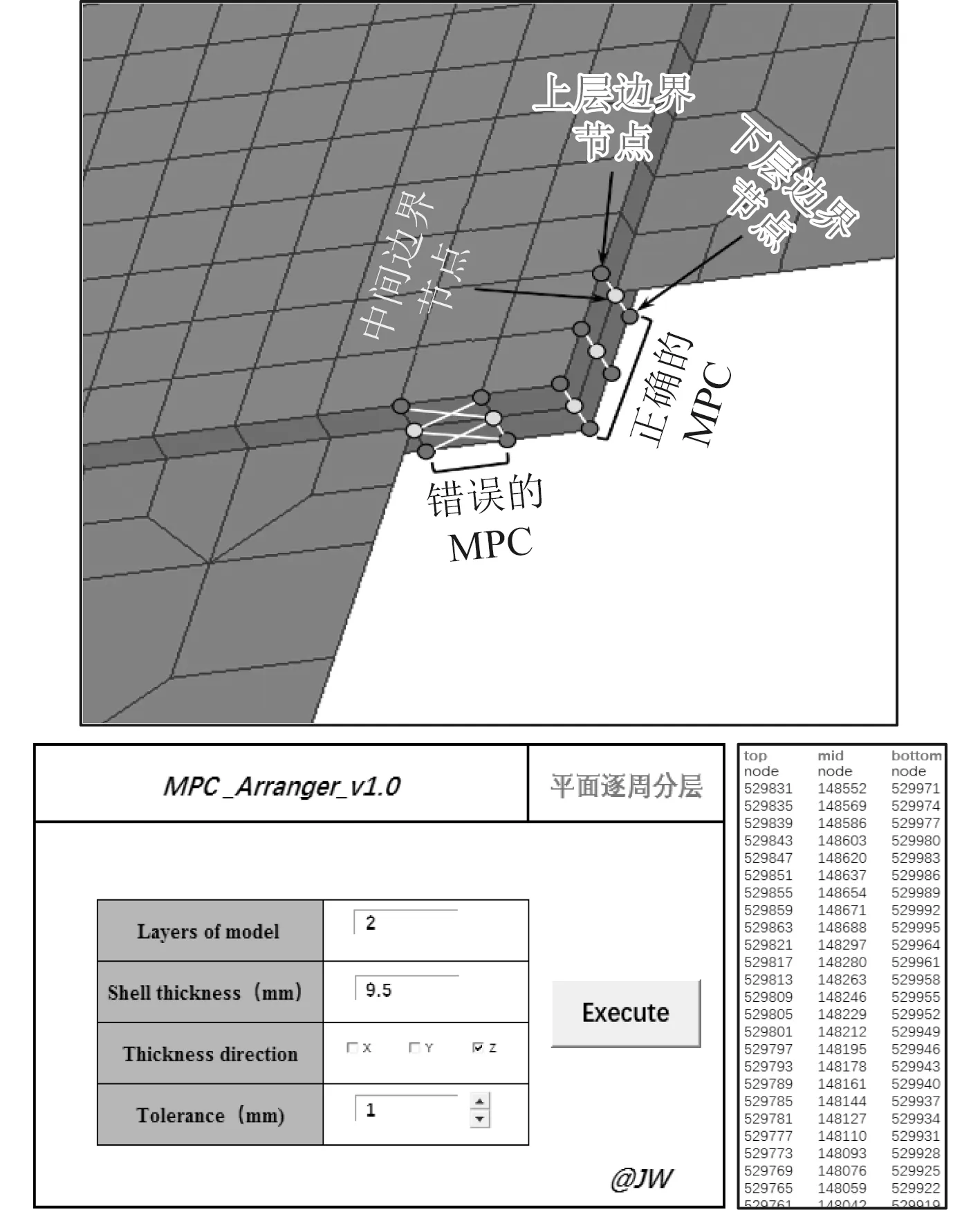
图2 边界MPC的创建Fig.2 Creation of boundary MPC
为解决MPC创建工作量大,效率低同时易出错的问题,本文提出“逐周分层”思想,分别以平板模型和部分典型曲面模型为例解释,并基于VBA语言编写插件MPC_arranger_V1.0进行高效实现,另外,本文所提体单元皆为8节点6面体solid单元。
2.1 平面逐周分层法
在船体结构的有限元模型中,以平板单元最为常见。如图3所示,以某简单平板为例,先对其中央区域进行网格细化,然后拖拽板单元建立实际厚度为t的壳体混合模型。以局部区域中心为原点O建立柱坐标系,以下皆以壳单元边界上任一待建立MPC的节点P为例,对逐周分层法做出解释。其中,O点和P点在原Patran总体坐标系中的位置分别为(xO,yO,zO)和(xP,yP,zP),可视作已知。
柱坐标系中P点相对O点的位置 (ρ,θ,z),可通过下列方程求得:
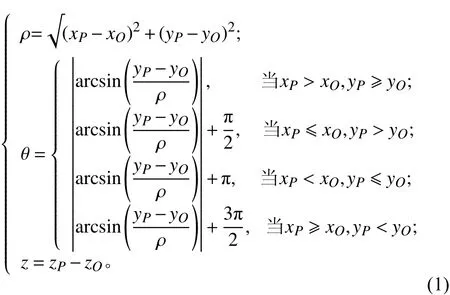

图3 平面逐周分层法Fig.3 Circum ferentially-layering in plane
通过Patran输出切割边界节点的位置信息,并使用插件进行逐周分层处理,即可快速实现各层边界点的重新排序,并汇总输出准确对应的各层节点号。相对GUI方式,视边界点节数量通常可将MPC创建效率至少提高百倍。
2.2 曲面逐周分层法
除常见的平板结构,船舶也存在诸多典型曲面结构物,本节针对部分应用广泛的典型曲面结构使用逐周分层法。
大多数潜艇艇体[21]及海洋平台结构[1,22]一般采用圆柱壳模型,图4为实际厚度为t的圆柱壳体混合模型。在圆柱坐标系中,外层节点所在圆柱面,中层节点所在圆柱面及内层节点所在圆柱面分别对应底部3个同心圆面,其中中层圆柱面的底圆面半径为r,将底圆面圆心O取为圆柱坐标系原点,以上参数视作已知。P点的圆柱系坐标 (ρ,θ,z)同式(1)。
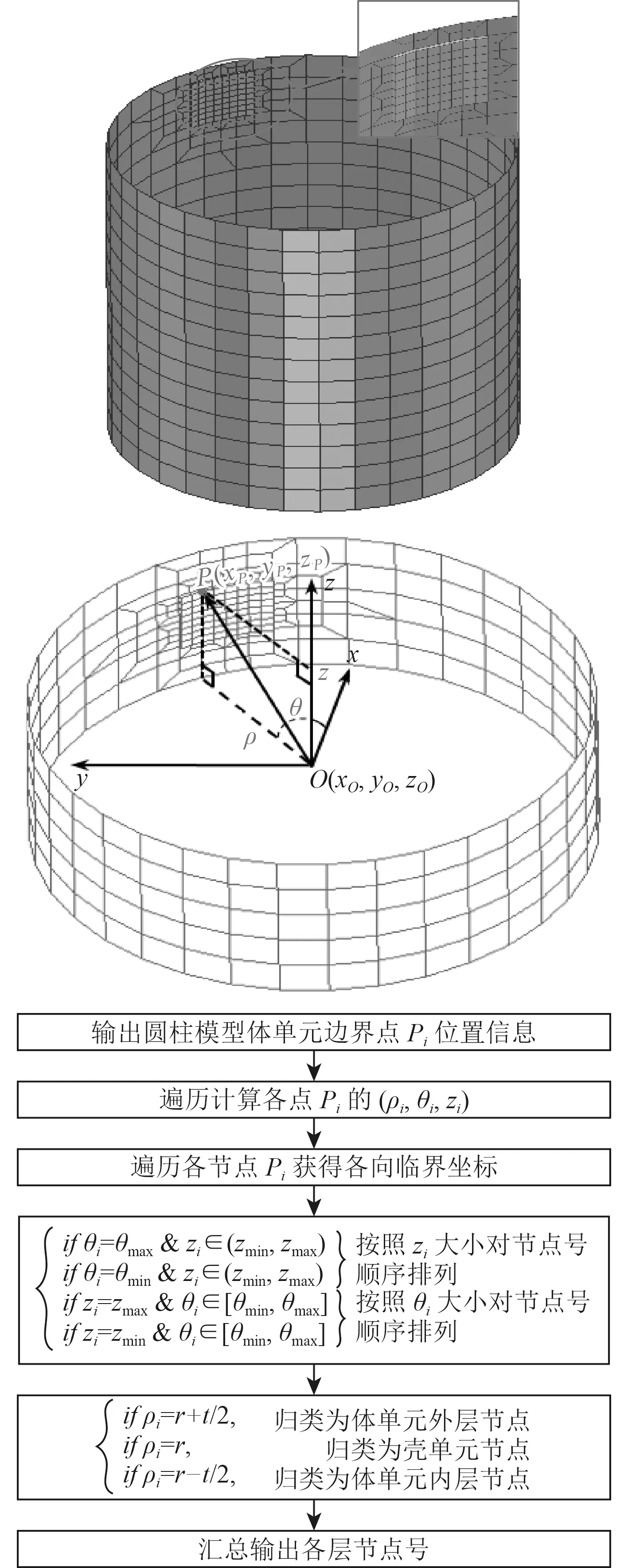
图4 圆柱面逐周分层法Fig.4 Circum ferentially-layering on cylinder
除圆柱壳模型应用广泛,椭圆柱壳由于其在装备布置和后屈曲性能方面的优势,也逐渐被应用于潜艇设计[23],如941型战略核潜艇。图5为实际厚度为t的椭柱形壳体混合结构。在椭柱坐标系中,外层椭柱面,中层椭柱面及内层椭柱面分别对应3个底椭圆面,其焦点分别为A1,B1,A2,B2和A3,B3,其中中层椭柱面的底椭圆长轴为a,将底椭圆面中心O取为椭柱坐标系原点,以上参数视作已知。
其中,P点的椭柱系坐标 (ρA2+ρB2,θ,z) 的分量θ和z见式(1), ρA2为P点与焦点A2点间的距离, ρB2为P点与焦点B2点间的距离,可通过下列方程求得:
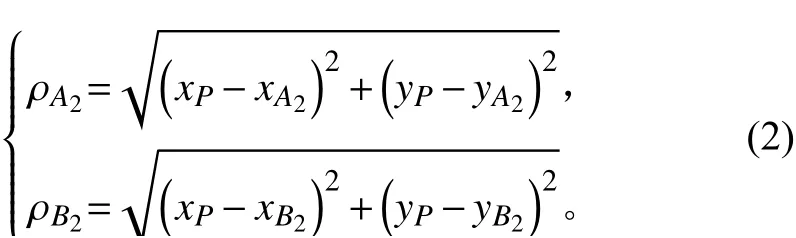
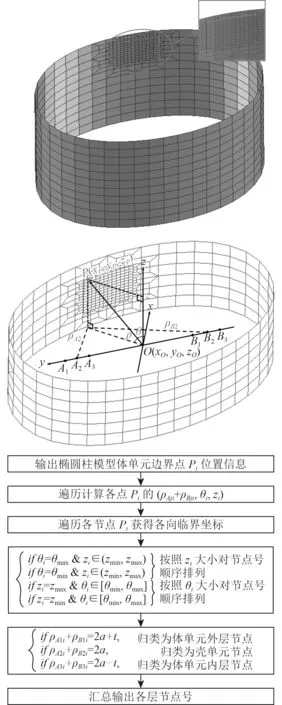
图 5椭柱面逐周分层法Fig.5 Circum ferentially-layering on elliptic cylinder
目前众多深水潜器[24]、潜艇艇首[25]、MOSS型LNG舱[26]都采用圆球壳模型,图6为实际厚度为t的圆球壳体混合模型。在圆球坐标系中,中层圆球面半径为r,原点O取在圆球中心,以上参数视作已知。
其中,P点的圆球系坐标 (R,θ,ϕ) 中分量θ表达式见式(1),R和 ϕ可通过下列方程求得:
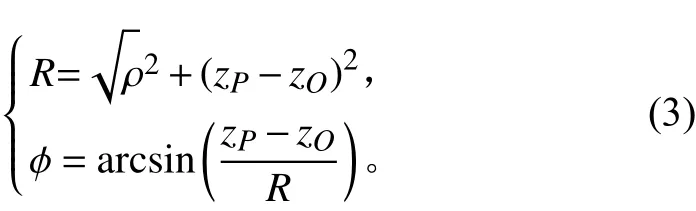
苏联部分Y级潜艇艇首采用椭球壳结构,图7为实际厚度为t的椭球壳体混合模型。在椭球坐标系中,外层椭圆截面,中层椭圆截面及内层椭圆截面的焦点分别为A1,B1,A2,B2及A3,B3,中层椭圆截面长轴为a,原点O取为椭球中心,以上参数视为已知。
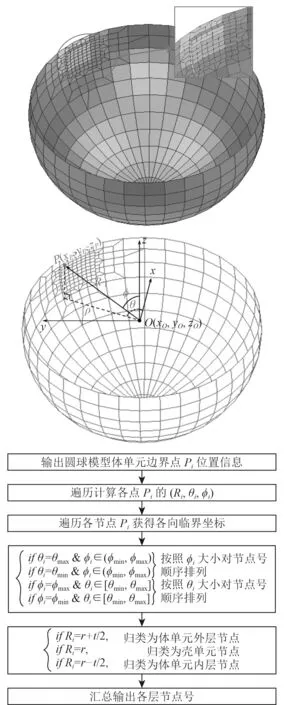
图6 圆球面逐周分层法Fig.6 Circum ferentially-layering on sphere
其中,P点的椭球系坐标 (RA2+RB2,θ,ϕ) 中分量θ和ϕ参见式(1)和式(3),RA2及RB2可由以下方程求得:
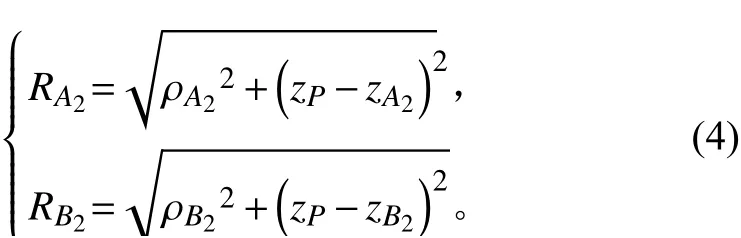
2.3 注意事项
针对本文所提逐周分层法,尚有几点说明:
1)逐周分层是一种方便MPC创建的思想。简言之,即先按边界点周向位置进行排序,再按层向位置归类,反之亦可,本文暂时采用先逐周后分层的手段。此外,在进行周向排序和层向归类时,判据并不唯一,本文仅取其中易于实现的一类判据进行实现。
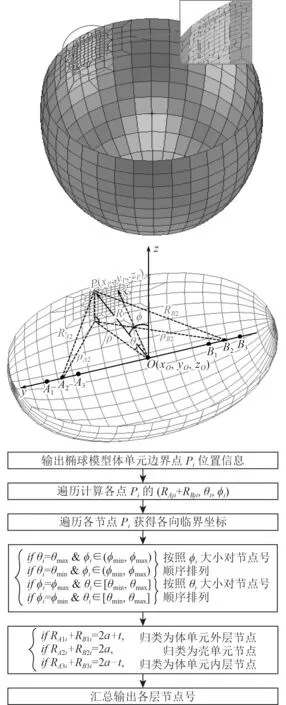
图 7椭球面逐周分层法Fig.7 Circum ferentially-layering on ellipsoid
2)使用逐周分层法具有一定的前提条件。各船级社疲劳评估规范均要求将局部区域的网格细化的较为规整,一是方便热点应力的插值,二是网格过渡和单元拖拽都比较简单,三是方便Ansys中子模型的建立。所以本文所提逐周分层法暂时考虑较为规整的边界。简言之,若整体模型对应位置处网格细化较为合理,这对于大多数复杂结构并不难实现,则推荐使用本文方法,若前期网格细化过于随意,会使切割边界及子模型的建立变得复杂,也会影响本方法的使用。
3)在实际操作中,各种误差均需考虑,如曲面网格光顺程度的影响,可直接在插件中进行设置。本文仅在理论层面进行说明,暂不涉及误差分析。
3 基于矩阵法的坐标变换
在Ansys中求解SIF,需要对体单元节点在原Patran坐标系中的位置进行坐标转换,并经插值才可施加为Ansys子模型的边界条件。闫小顺[1]自编patran2ansys宏插件完成此部分工作,但插件中需要输入不同坐标系间的相对平动及转角位移,才能实现坐标转换。实际上,这仅可推广于部分较为简单的平动坐标变换,对于转动坐标变换,存在以下问题:
1)两坐标系各平面间的相对转角其实并不直观,即便先通过计算方向向量来求得各向转角,也费诸多周折。
2)体单元中或存在成千上万的节点,若每次求解SIF均通过Ansys APDL处理坐标变换,在批量求解各尺寸裂纹的SIF时,也会增加前处理的负担。
为解决以上问题,本文保留patran2ansys插值部分功能,并使用VBA语言编写插件FEM_coor_transfer_V 1.0,基于转换矩阵法对其坐标变换部分进行改进,原理如下:

为保证转换矩阵可逆,式中(p1,q1,r1),(p2,q2,r2),(p3,q3,r3)需取为Patran体模型中任意不共线的3个节点坐标,这里推荐选取易于识别的体单元边界点。(a1,b1,c1),(a2,b2,c2),(a3,b3,c3)为Ansys子模型中与上述3点对应的节点坐标,这种对应是指几何形状的对应。 (xp,yp,zp)为 Patran中某待转换节点坐标;(xa,ya,za)为Ansys中待求节点坐标; (xO,yO,zO)为Patran坐标系原点坐标。简言之,本文所提矩阵变换法更关注模型的宏观几何形状,并不考虑坐标系间的相对位置关系。根据公式(5)及Patran中可输出的原节点坐标,经FEM_coor_transfer_V1.0处理后可直接输出指定格式的节点坐标信息,方便实现子模型边界信息交互。
4 基于映射网格的裂纹建模
求解复杂载荷下构件中的裂纹扩展问题需要计算不同尺寸裂纹的SIF,若通过部分裂纹的SIF推得所有可能的SIF,一般采用拟合公式或插值的方法。拟合公式工作量较大,只有对常见的结构,如纵骨端部[27],才有必要进行拟合,对于不常见或没有经验公式可用的结构,插值也是一种推荐的手段。但插值中存在外插准确性不高的问题,故应尽可能地采用内插值方式,前提是必须最大限度地获取所有可能出现的裂纹的SIF。
5 子模型技术的验证
如图8所示,本节以某B型LNG燃料舱舱顶横向支座处弧形肘板趾端处的疲劳热点为例,按照规范对热点进行不少于10t范围的t×t细化,并对热点所在底板在板厚方向设置4层体单元,采用改进的子模型技术及所编插件,完成热点处各壳体单元间MPC的创建、节点坐标转换及裂纹SIF的求解。目标舱段的疲劳载荷根据ABS规范中的疲劳工况施加,包括迎浪、横浪及斜浪工况。

图8 疲劳热点及子模型Fig.8 Fatigue hotspot and sub-model
对复杂载荷或复杂结构使用子模型技术,参考DNV规范,需对边界条件进行验证。如图9所示,本文选取对横向肘板趾端影响较大的横浪工况进行验证,经对比,可见Patran中体单元和Ansys子模型的边界及整体位移吻合度较高,可证明本文所提子模型技术的合理性。
上述疲劳热点处构件尺寸及裂纹位置如图10所示,其中T1=30mm,L=25mm,B=9.5mm,T2=12mm。
裂纹SIF大小受复杂载荷成分及焊趾的影响。此处焊缝2L较长且板厚B较小,参考ABS规范,并考虑裂纹实际扩展情况,a取0.5~9 mm,a/c取0.15和0.2,I型SIF计算结果如图11所示。
6 结语
本文针对使用子模型技术求解复杂载荷下裂纹SIF时各环节存在的问题,结合Patran和Ansys两款有限元软件,基于VBA及APDL语言,进行如下改进:
1)针对壳体单元间MPC的创建低效问题,提出更加高效的逐周分层法并编写插件M PC_arranger_V1.0进行实现。给出对平板及各典型曲面结构进行逐周分层的相关公式及逻辑流程,且成功应用于舱体疲劳热点处MPC的快速建立。相对GUI操作,一般视边界点数量可将MPC创建效率提高数百倍,具有一定推广意义。

图9 横浪工况Fig.9 Beam sea load case

图10 裂纹位置及构件尺寸Fig.10 Crack location and component size
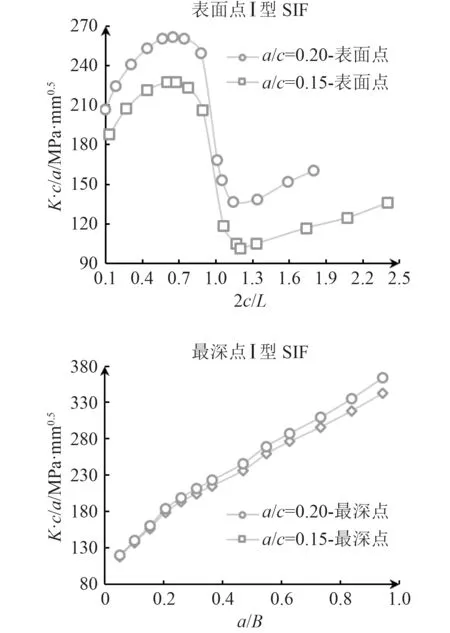
图11 I型裂纹SIFFig.11 Mode-ISIFof crack
2)针对不同坐标系间节点位置转换困难问题,提出更加直观的矩阵法并编写插件FEM_coor_transfer_V1.0进行实现,且成功应用于舱体疲劳热点位置处的节点坐标转换。
3)针对非常见构件求解裂纹SIF时自由划分方式的局限性,提出更具优势的映射划分方式并编写插件Crack_mapper_V1.0进行实现,且成功应用于舱体疲劳热点处各尺寸表面裂纹的SIF求解。

