一种基于2D-CNN的激光超声表面缺陷检测方法

（大连理工大学 机械工程学院，辽宁 大连 116024）

引言

激光超声无损检测凭借其高分辨率、宽频带、多模态的特点以及检测过程中无需耦合剂、可实现远距离无接触多次扫描的优势，在无损检测领域受到了广泛关注[1-3]。围绕激光超声缺陷检测以及定量表征这一课题，国内外学者开展了大量的研究工作。Lei Yang[4]等提出了一种基于连续小波变换（CWT）的激光生成lamb 波透射系数计算算法，成功预测了薄结构中的缺口深度；F.Hernandez-Valle 等[5]利用激光激发Rayleigh 波实现对表面缺陷几何形状的测量，通过对超声信号的分析得到的信息表征缺陷的几何形状；黄燕杰、尚建华等[6]运用有限元数值模拟的方法研究了表面波在复合材料中波形与裂纹深度和宽度的时间关系，实现对缺陷的定量检测；陶程等[7]采用有限元法研究了表面波与缺陷之间的相互作用，通过超声波传播与缺陷之间的时间关系实现对缺陷深度的定量检测。超声检测的关键在于对信号的处理与解释，进而对缺陷进行定性定量分析，上述研究成果主要通过超声波与缺陷相互作用的时间关系或通过信号处理提取特征的方式实现对缺陷的定量分析，很大程度上依赖操作者对信号的判读，容易出现误判、漏判的情况，难以保证检测结果的稳定[8]。

为了保证检测结果的稳定性，基于深度学习[9-10]在图像识别、目标检测等领域的成功应用，有学者尝试使用深度学习算法实现超声缺陷的自动检测，以减少人工操作对检测结果的影响，取得了良好的效果。李萍[11]等较为详细介绍了深度学习在超声缺陷检测中的应用与发展。Qiuji Yi 等[12]提出了基于小波包融合算法结合支持向量机（SVM）的激光超声定量检测。Min Meng 等[13]提出使用小波变换提取小波系数训练卷积神经网络（CNN）对碳纤维聚合物的缺陷分类。目前提出的基于深度学习的激光超声检测方法都需要手动提取缺陷特征来训练网络模型，而手工提取特征过程复杂，提取的质量对网络模型的训练效果有很大影响，需要相关人员具有较高的技术水平。

针对上述问题，借鉴深度学习在图像识别领域的成果，利用卷积神经网络（CNN）强大的表征学习能力，不同于以往的人工提取缺陷特征训练分类检测模型的方式，本文提出了一种基于二维卷积神经网络（2D-CNN）激光超声缺陷检测方法，直接将缺陷的小波时频图作为输入训练CNN模型，免去了复杂的特征提取步骤，实现对表面缺陷的自动分类。

1 基本原理

1.1 连续小波变换

小波变换（wavelet transform）采用随频率改变的“时间-频率”窗口，以克服短时傅里叶变换（STFT）中窗口大小不随频率或时间变化、无法准确反应频率与时间变化关系等缺点，更适合处理夹带瞬态突变的超声信号。本文选择使用连续小波变换[14]（CWT）对信号数据进行预处理，其数学定义为

其中：f（t）为任意的L2（R）空间中的函数；a为尺度因子，表示与频率相关的伸缩；τ为平移因子；ψ（a，τ）（t）为小波基函数。当a取值较大时，适合提取信号中的低频特征，反之则适合提取高频特征。

小波变换的关键在于小波基函数的选择，其决定了小波变换的效果和效率。常用的小波基函数有Haar 小波、Coiflets 小波、Morlet 小波和cmor 小波等。由于Morlet 小波的几何形状与超声回波波形相似[15]，而cmor 小波是Morlet 小波的复数形式，具有更好的自适应能力，因此本文选择cmor 小波作为连续小波变换的小波基函数。借助Matlab的wavelet toolbox 工具箱，对采集到的时序信号进行处理，得到含有超声信号时频域信息的二维时频图像。

1.2 卷积神经网络

卷积神经网络[16]（CNN）是一种包含卷积计算且具有深度结构的前馈神经网络，凭借其强大的表征学习能力在图像识别、目标检测和机器视觉等领域广泛应用。其结构通常由输入层、卷积层（convolutional layer）、池化层（pooling layer）、全连接层和输出层构成，图1为根据缺陷分类需要所建立的CNN模型。

图1 卷积神经网络结构图Fig.1 Structure diagram of convolutional neural network

1）卷积层：卷积层是神经网络模型中最重要的组成部分，其作用是提取局部区域的特征，不同层的卷积核相当于不同的特征提取器。同全连接神经网络相比，具有局部链接和权重共享2个突出的性质，可以显著减少神经网络的参数数量。卷积运算的数学形式为[16]

式中：z（l）为第l层的输出；滤波器w（l）为可学习的权重向量；a（l−1）为l−1层的输出；b(l)∈R为可学 习的偏置。

2）池化层：池化层的主要作用是减小输出特征的维度，防止过拟合，常用的池化运算包括最大池化（max pooling）和平均池化（average pooling）。本文选择最大池化，数学表达式为[16]

其中xi是区域内每个神经元的激活值。

3）全连接层：作为卷积网络与分类器之间的过渡结构，将Flatten函数展平得到的一维数组与分类函数Softmax 连接起来。

1.3 2D-CNN 方法

利用小波变换在信号时频域分析的优点和CNN 图像识别方面优异的性能，使用CWT 对激光超声信号进行时频处理，得到小波时频图用于训练卷积神经网络模型，实现对表面缺陷的识别和分类。具体步骤如下：

1）将采集到的超声信号进行整理，剔除其中的无效信号，构造样本数据集；

2）使用CWT 对整理好的样本集进行预处理，生成超声信号的小波时频图，得到图像样本，将图像样本随机打乱，按照一定比例划分为训练集、验证集和测试集；

3）构建CNN模型，使用划分好的训练集训练神经网络并根据训练结果调整参数，优化网络性能；

4）使用测试集对训练好的CNN模型进行测试，测试CNN模型的检测精度及泛化能力。

2 方法验证

2.1 数据获取和处理

本文使用有限元仿真软件Comsol Multiphysics模拟激光激发超声波检测带涂层工件的表面缺陷来获得缺陷检测信号，仿真步骤如图2所示，缺陷检测模型如图3所示。模型长度L=25 mm，总厚度H=10 mm，涂层厚度为h=50 μm，缺陷位置位于距离激光束光斑中心L1=15 mm 处，缺陷宽度0.5 mm，深度分别设置为0.5 mm、1.0 mm、1.5 mm 和2.0 mm，信号采集区域选择距激光束光斑中心L2=4 mm 和L3=11 mm的B、C点之间，采样频率为10 MHz，通过信号采集装置对此区域进行扫掠，可以获得连续的超声波传播信号。

图2 有限元仿真流程图Fig.2 Flow chart of finite element simulation

图3 模型图Fig.3 Model diagram

在有限元仿真过程中为了更接近真实情况，将脉冲激光辐照被测工件的过程等效为加载热力源的形式[17]，基于热弹效应[18]模拟了激光超声检测5种类型的带涂层铝板，分别为defect_0（无缺陷）、defect_05（缺陷深度0.5 mm）、defect_10（缺陷深度1.0 mm）、defect_15（缺陷深度1.5 mm）和defect_20（缺陷深度2.0 mm），每种缺陷类型分别采集800组超声波反射信号，共得到4000组检测信号。

图4所示为模型同一位置、不同表面缺陷深度条件下的超声反射信号时域波形图，分别为无缺陷表面和4种不同深度表面缺陷的波形。从图4（a）中可以看出在不同缺陷深度下，直达表面波R 基本重合，反射波RR之间存在着一定的差异，但反映在时域波形图上差异并不明显，即便对于专业检测人员来说，对缺陷深度做出定量解释也需要进行复杂的计算，而在实际检测当中还会夹杂有噪音干扰以及涂层对声波传播的影响，增加了评价的难度，难以保证检测结果的准确和稳定。

图4 不同缺陷深度的时域波形图Fig.4 Time-domain oscillograms of different defect depths

如1.1节所述，在Matlab的wavelet toolbox 工具箱中，选择CWT 对样本数据集进行批量处理，得到小波时频图，共得到5类缺陷共4000 张样本图片。将图片输入神经网络前需要对图片大小进行统一，在满足神经网络输入要求和尽可能保存多的图像信息的条件下，保存为300×300像素分辨率大小，并随机打乱，按照7∶2∶1的比例将图片划分为训练集、验证集和测试集，各数据集之间相互独立，数据集划分见表1。图5为不同缺陷深度的小波时频图。

2.2 卷积神经网络的构建

基于LeNet[19]神经网络模型，搭建了如图1所示的CNN网络：输入图像的像素大小为300×300；中间层由3个卷积层和3个池化层组成，卷积核的大小均为5×5，深度依次为32、64 和128，池化层选择最大池化（max pool），其作用是减少神经网络中参数的个数。为避免出现过拟合现象，在Flatten层后面引入了Dropout层，Dropout层作用时在每次训练中以概率P 随机冻结神经元，P取0.25。同时在每个卷积层和池化层之间添加了批量归一化层（batch normalization），激活函数选择ReLU 激活函数，使用Softmax 分类器进行分类，神经网络模型中的具体参数见表2。

表1 不同类型缺陷数据集划分Table1 Division of different types of defects data sets

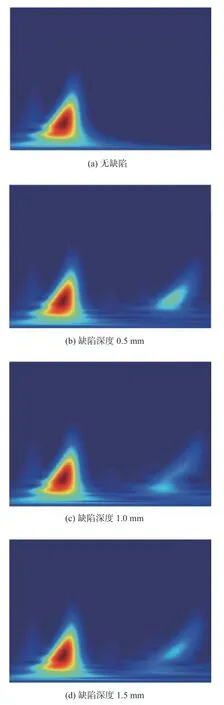
图5 不同缺陷深度的小波时频图Fig.5 Wavelet time-frequency diagram of different defect depths

表2 卷积神经网络模型参数Table2 Model parameters of convolutional neural network

在训练过程中，为了提高CNN模型对缺陷分类的准确率及模型的泛化能力，需要根据训练结果对网络参数进行优化调整，本文选取不同的学习率和不同的优化器以获得最佳的神经网络模型。在训练过程中，卷积神经网络的学习率分别设置为0.00005 和0.0001，依次选择Adam、RMSprop 和SGD 优化算法，损失函数选择交叉熵函数（cross entropy），batch_size 设置为64，训练轮数设置为20个Epoch，为消除随机因素的影响，对每个学习率和优化算法进行多次训练，结果取平均值。训练过程在一台Win10 操作系统的计算机上完成，硬件配置为：CPU为AMD R5 2600；GPU为英伟达GTX1060 5G；16G 运行内存。使用Python在Tensorflow+keras 环境下搭建CNN模型。图6表示在不同学习率下，3种梯度下降算法在CNN模型训练过程中损失值以及准确率的变化曲线。

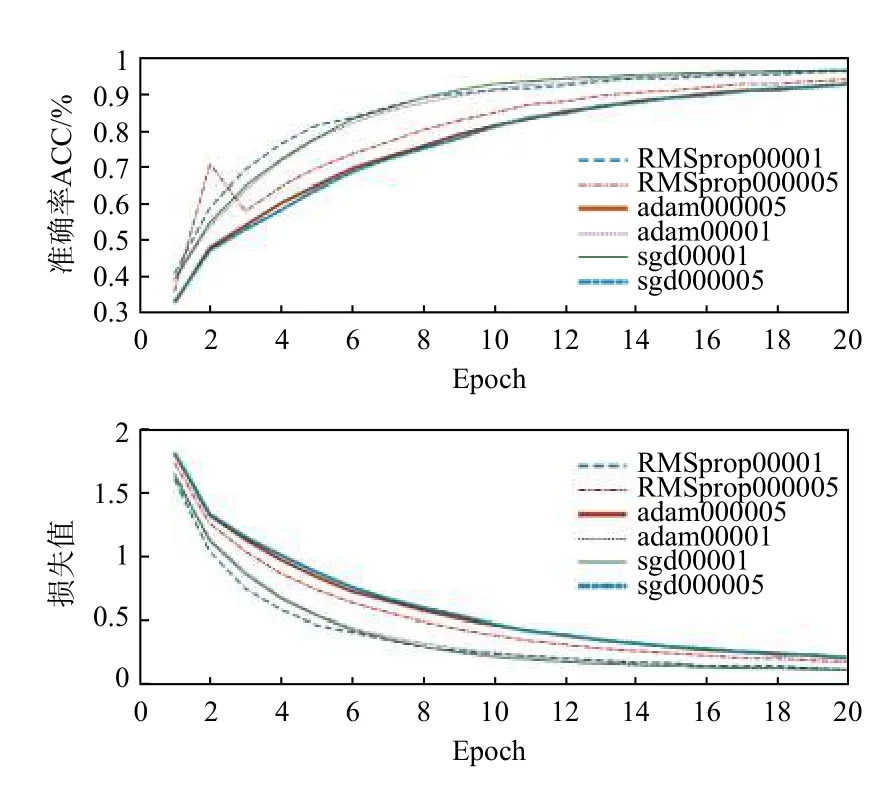
图6 神经网络训练过程曲线Fig.6 Neural network training process curve

表3 3种优化器在不同学习率下的损失值Table3 Loss values of three optimizers at different learning rates

表4 3种优化器在不同学习率下的准确率Table4 Accuracy rate of three optimizers at different learning rates

表5 5次测试结果Table5 Five test results

3 结果与分析

为了使分类模型获得最优效果，将2.2节中提到的学习率和优化算法分别训练5次，得到CNN分类模型的平均损失值和准确率如表3、表4所示。可以看出，将学习率设置为0.0001时损失值和准确率的表现优于将学习率设置为0.00005时的表现；SGD 优化器在训练集上的损失值和准确率效果最好，而Adam 优化器在验证集和测试集上的损失值和准确率要优于SGD 优化器。对以上结果综合考量，将CNN 分类模型的学习率设置为0.0001、选择Adam 优化器时的效果最好，该CNN模型运行5次的测试准确率如表5所示，其对测试集的识别准确率均达到了96%以上，平均准确率为97.3%，可见CNN模型对表面缺陷的识别分类达到了较高的准确率且检测稳定性良好。

为了验证模型的泛化能力，使用新的缺陷时频图对训练好的模型进行测试，表6所示为CNN模型将输入的测试样本准确识别为目标分类的概率，结果显示模型识将被测对象正确分类的概率达到98%以上，说明CNN模型具有良好的泛化能力。

表6 对单一缺陷深度进行测试的识别准确率Table6 Identification accuracy rate of single defects depth test

4 结论

针对激光超声表面缺陷检测过程中，缺陷定量表征对操作者依赖程度高所带来的检测结果不稳定问题，借鉴深度学习在图像识别领域的成果，提出一种基于2D-CNN的激光超声无损检测方法。该方法使用小波时频图作为输入训练卷积神经网络，CNN 自动提取和学习图像中的缺陷特征，实现对缺陷深度的自动分类，为激光超声缺陷检测提供了新的思路。

1）根据训练的结果对神经网络的参数进行优化，得到的CNN模型可以实现对不同深度的缺陷自动分类，测试的平均准确率达到了97.3%，检测结果可靠，在后续的研究中可以尝试使用不同的网络结构和算法以提高准确率。

2）使用CNN模型检测随机类型的超声信号，CNN模型的识别正确率可以达到98%以上，分类模型具有较强的泛化能力。

3）所提出的缺陷检测方法可行有效，缺陷的小波时频图能够准确反映超声信号携带的时频特征，卷积神经网络能够从时频图中提取和学习缺陷特征，实现对缺陷类型的自动分类，免去了人工提取缺陷特征的步骤，能够有效避免因人为主观因素导致的检测结果不稳定。