圆形阵列光电探测系统双目标识别方法

高丰佳，董 涛，谭林秋，开百胜

（1.西安工业大学 陕西省光电测试与仪器技术重点实验室，陕西 西安 710021；2.中国兵器工业集团有限公司 黑龙江北方工具有限公司，黑龙江 牡丹江 157000）

引言

在枪、炮、弹的研制和生产中，弹丸着靶密集度是评估武器杀伤效能优劣的重要指标，而武器系统射击密集度的测量一般是通过先对弹丸着靶坐标的测量，进而通过相应密集度公式计算而来的[1-2]。对于单发武器和低射频连发武器，其弹丸着靶坐标采用现有的各种自动化测量方法不难进行测量；而对于多管齐射武器和高射频转管武器，在测量其弹丸着靶坐标时，往往存在2发弹丸同时着靶的情况。针对弹丸着靶坐标的测量，传统的方法为木板靶或网靶法，靶板法不能识别重孔，对于连发射击不能识别弹序，且存在费时、费力、人为判读误差较大等问题。目前常用弹丸着靶坐标自动测量方法有声学原理的方法[3-5]、多光幕交汇测量法[6-9]、半导体器件阵列测量法[10]、双CCD 交汇测量法[11-14]。这些方法都有各自的优点，但都存在一个共同的问题：当有2发及其以上弹丸同时着靶时，现有各种自动化测量设备均存在测量系统复杂的问题。

有研究者提出采用4台高速线阵CCD 相机，组成3个测量靶面测量双目标同时着靶情况下的坐标[15]，当2发弹丸同时着靶时，通过2发弹丸在3个测量靶面间的成像关系以及弹丸飞行速度约束，得到2发弹丸的着靶坐标。该方法采用较多的CCD 相机，不但增加了系统成本，而且使得测量系统较为复杂。另有研究者提出了七光幕阵列测试原理，即在双V形六光幕阵列中增加一个光幕组成七光幕阵列[16]，并构建时间序列算法来识别双目标同时着靶，该方法同样具有系统结构复杂的缺点。

针对2发弹丸同时着靶情况下的坐标测量所存在的问题，本文提出一种基于圆形光电探测阵列的双弹丸同时着靶坐标测量方法，建立了系统测量数学模型，给出了弹丸着靶坐标测量公式，并通过软件对坐标测量误差进行了分析和仿真。

1 测量原理与模型

图1为基于圆形光电探测阵列的双弹丸同时着靶坐标测量系统总体组成示意图，系统主要由靶架、3个扇形一字线激光器、圆形光电探测阵列以及相应的信号处理电路组成。3个激光器A、B和C在圆形靶框上均匀分布，其中1个激光器位于靶框正上方，另外2个分别位于靶框左下方和右下方，3个扇形一字线激光器将圆形光电探测阵列分成3段，每一个激光器发出的光线投射到对应位置的光电探测阵列上，激光器的发光波段为780 nm，所以在圆形光电探测阵列的前面设置一个中心波长为780 nm的窄带滤光片，防止其他波段的杂散光线对系统的干扰。

图1 系统总体组成示意图Fig.1 Schematic diagram of photoelectricity measurement system

图2为系统弹丸投影示意图，当2发弹丸E1和E2同时穿越探测光幕面时，激光器A通过2个弹丸E1和E2在圆形光电探测阵列上留下投影A1和A2，同样，激光器B通过2个弹丸E1和E2在圆形光电探测阵列上留下投影B1和B2，激光器C通过2个弹丸E1和E2在圆形光电探测阵列上留下投影C1和C2，圆形光电探测阵列对应的信号处理电路识别出6个弹丸投影点A1、A2、B1、B2、C1和C2在圆形光电探测阵列上的中心位置。分别连接点A和A1、A和A2、B和B1、B和B2、C和C1、C和C2，形成6条直线AA1、AA2、BB1、BB2、CC1和CC2，6条直线形成的交点中，只有3条直线同时相交的点为真实弹着点，其余交点为虚假弹着点，这样便可以对2发弹丸的着靶坐标进行识别。

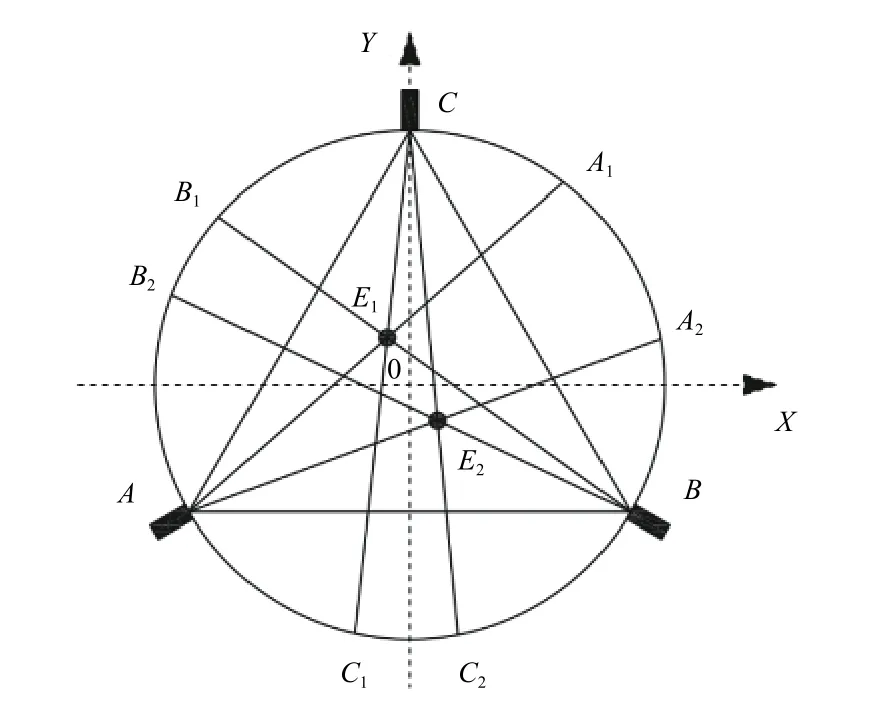
图2 弹丸着靶坐标计算示意图Fig.2 Calculation diagram of coordinate for projectiles passing through detection area

以圆形靶框的中心点O为原点，以X轴的正方向为极轴，建立极坐标系，圆形半导体光电探测阵列围成的圆半径为R，所以激光器发光点A、B、C的极坐标分别为A（R，210°）、B（R，330°）、C（R，90°），6个弹丸投影点A1、A2、B1、B2、C1和C2可通过圆形光电探测阵列对应的信号处理电路识别得到，设6个投影点的极坐标分别为：A1（R，θA1）、A2（R，θA2）、B1（R，θB1）、B2（R，θB2）、C1（R，θC1）和C2（R，θC2）。

同样以圆形靶框的中心点O为原点，建立直角坐标系XOY，则激光器发光点A、B、C对应的直角坐标分别为：A（Rcos210°，Rsin210°）、B（Rcos330°，Rsin330°）和C（Rcos90°，Rsin90°），6个投影点对应的直角坐标分别为：A1（RcosθA1，RsinθA1）、A2（RcosθA2，RsinθA2）、B1（RcosθB1，RsinθB1）、B2（RcosθB2，RsinθB2）、C1（RcosθC1，RsinθC1）和C2（RcosθC2，RsinθC2）。

设弹着点E1的极坐标坐标为（ρ1，θ1），弹着点E2的极坐标坐标为（ρ2，θ2），则弹着点E1的直角坐标为（ρ1cosθ1，ρ1sinθ1），弹着点E2的直角坐标为（ρ2cosθ2，ρ2sinθ2）。

直线AA1的两点式方程为

化简得到直线AA1的方程为

同理，可得直线AA2的方程为

直线BB1的两点式方程为

化简得到直线BB1的方程为

同理，可得直线BB2的方程为

联立直线AA1和直线BB1的方程得：

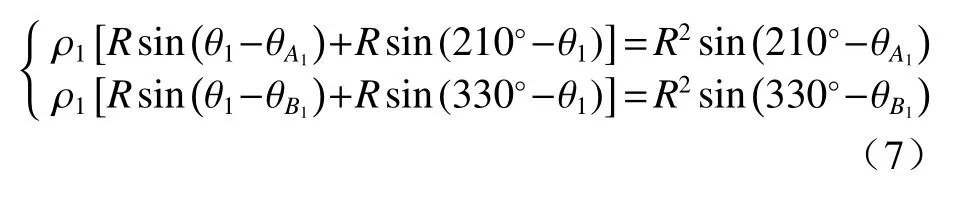
两式相除并化简得：

将其带入公式（2）直线AA1的方程可得：

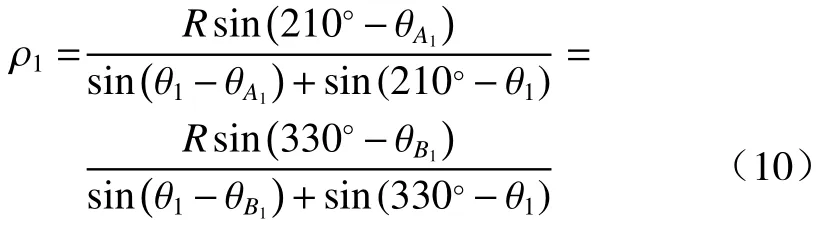
所以弹着点E1的直角坐标系坐标为

式中θ1如公式（9）所示。

同样联立直线AA2和BB2的方程得：

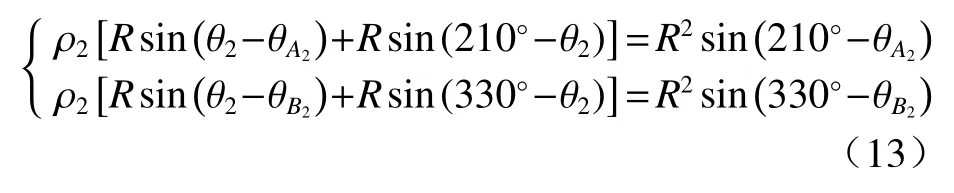
解方程组（13）可得弹着点E2的直角坐标系坐标为

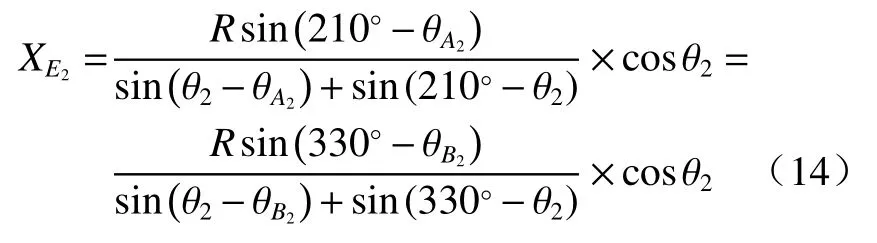
其中：

2 坐标测量误差分析和仿真

由点E1的直角坐标（XE1，YE1）中的XE1与YE1的公式可以看出，XE1与YE1分别是自变量R、θ1、θA1的函数，因此XE1与YE1的测量误差标准差σXE1与σYE1分别为

式中，ΔR=（R/1 000）mm是圆的半径R的误差，∂XE1/∂R，∂YE1/∂R分别为XE1，YE1对求R偏导所得到的误差传递系数；ΔθA1=（1/2πR）×2π是A1点极坐标的角度误差，∂XE1/∂θA1，∂YE1/∂θA1分别为XE1、YE1对θA1求偏导所得到的误差传递系数；ΔθB1=（1/2πR）×2π是B1点极坐标的角度误差，∂XE1/∂θB1、∂YE1/∂θB1分别为XE1、YE1对θB1求偏导所得到的误差传递系数。

当半径R的值为1.5 m时，以O点为原点取圆形正中心1 m×1 m的靶面进行仿真，取ΔR=1 mm，ΔθA1=0.001°以及ΔθB1=0.001°，则如图3所示，该图为弹丸穿过探测幕面时的弹丸着靶坐标测量误差分布图，图3（a）为X坐标测量误差的变化分布图；图3（b）为Y坐标测量误差的变化分布图。

图3 圆形阵列光电探测系统X和Y坐标测量误差分布Fig.3 Error distribution of coordinates X and Y based on circular array photoelectricity detection system

1）从图3（a）中可以看出，X坐标测量误差只随Y坐标的增加而减小，与X坐标值的变化无关；X坐标测量误差关于坐标X=0对称；在靶面为1 m×1 m时，X坐标测量误差标准差最大为2.722 mm。

2）从图3（b）中可以看出，Y坐标测量误差关于坐标X=0对称，距坐标X=0越远，Y坐标测量误差越大；Y坐标测量误差关于坐标Y=−170对称，距坐标X=0越远，Y坐标测量误差越大；在靶面为1 m×1 m时，Y坐标测量误差标准差最大为0.57 mm。

3 实验与结果分析

为验证系统在双弹丸同时着靶状态下的坐标测量功能及测量精度，用2 根带磁性的钢棒模拟2发弹丸，将2 根钢棒同时吸附于表面粘贴有坐标纸的钢板上的任意位置，如图4所示。本文所提双弹丸同时着靶坐标测量系统的3个激光器组成的探测光幕和纸靶的测量靶面平行且距离较近，约为10 mm，所以2个模拟弹丸均可进入由3个激光器和圆形的光电探测阵列组成的探测光幕，并且通过3个激光器在圆形的光电探测阵列上形成6个模拟弹丸的投影，采用圆形光电探测阵列对6个弹丸投影信号进行光电转换，并进一步通过信号处理电路对6个弹丸投影在圆形光电探测阵列上的中心位置进行识别，最后通过系统弹丸着靶坐标测量公式（11）、（12）、（14）和（15）计算得到每一组2个模拟弹丸的坐标，测量5 组共10 发，实验数据如表1所示。

图4 模拟2发弹丸同时着靶装置Fig.4 Experimental figure of two projectiles passing through detection area at same time

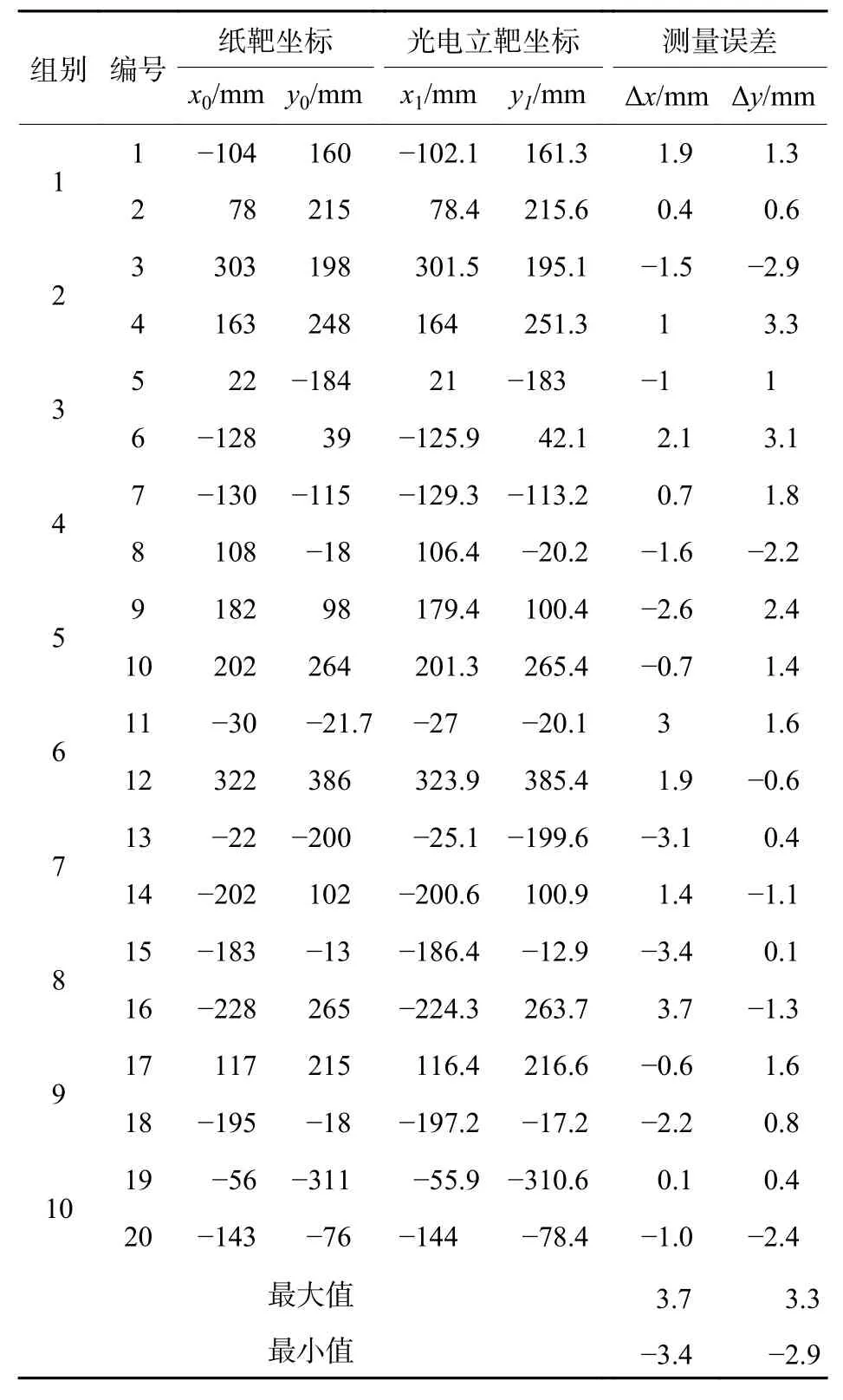
表1 模拟双弹丸同时着靶坐标测量实验数据Table1 Experimental data on measuring simulation of dual targets impacting coordinate

从表1中实际测量结果可以看出，本文提出的基于圆形光电探测阵列的双弹丸同时着靶立靶坐标测量系统功能正常，所述双弹丸信号处理方法有效。表1中得出的x坐标测量误差的绝对值最大为3.7 mm，y坐标测量误差的绝对值最大为3.3 mm；但是，纸板坐标测量过程中会存在弹孔识别误差与卷尺读数误差，其均属于随机误差，本实验中认为弹孔识别误差小于±0.5 mm，卷尺读数误差小于±0.5 mm。因此，最终可以得到x坐标测量误差的绝对值最大为4.7 mm，y坐标测量误差的绝对值最大为4.3 mm；x坐标测量误差标准差σX和y坐标测量误差标准差σY分别为2.22 mm 和1.98 mm。

4 结论

本文提出并研究了基于圆形阵列的双弹丸同时着靶坐标测量方法，采用3个发光角度均为60°的扇形一字线激光器和圆形光电探测阵列形成系统测量探测幕面，当有2发弹丸同时穿越该测量探测幕面时，会在圆形光电探测阵列上留下6个弹丸投影，通过信号处理电路进行识别，得到6个弹丸投影在圆形光电探测阵列上的中心位置，根据系统参数以及弹丸投影的中心位置，推导了双弹丸着靶坐标测量公式，并通过软件对坐标测量误差进行了分析和仿真，结果表明，当有双弹丸穿越1 m×1 m的探测幕面时，本系统的X坐标测量误差标准差最大为2.7 mm，Y坐标测量误差标准差最大为0.6 mm。通过带有磁性的2 根钢棒模拟双弹丸同时着靶，对所提系统进行了模拟实验验证。结果证明，本文所提的双弹丸测量方法可行，10组20 发的X坐标测量误差标准差σX和Y坐标测量误差标准差σY分别为2.22 mm 和1.98 mm。仿真与实验数据均证明本文所提出的系统可以有效测量弹径4.5 mm 及其以上的双弹丸着靶坐标。该系统同样适用于单发弹丸的着靶坐标测量。