影响潜水层基坑降水引起地面沉降的因素分析

刘 冠 杰

(烟台大学土木工程学院，山东 烟台 264005)

0 引言

随着进入21世纪以来，我国的工业化和城市化高速发展，建筑物逐渐向着两端延长，且更加高耸和地下空间更加宽阔。不断出现的高层建筑，随之会出现极多的深基坑工程，人口的密度上升和交通的压力，也使得地下交通盛行，这些工程势必会对现有的基坑规范提出更严格更准确的要求。尤其是在沿海等地下水埋深较浅的地区，解决降低地下水对周围环境造成的问题成为基坑能否顺利开挖的必要因素[1,2]。

目前基坑工程的降水方法主要有主动降水和被动止水两大类，但无论是主动降水还是被动降水，势必导致土层间地下水的水位变化，从而导致地面的不均匀沉降，不利于基坑的稳定和周围建筑物的安全甚至会引起建筑物的开裂和倒塌。基坑开挖前的降水可以有效提高开挖土体的稳定性，防止流沙和坍塌等现象的发生，使施工可以在相对干燥的环境下进行，同时加速软土地基的固结，提高软土的强度和承载力[3,4]。

1 降水引起沉降的基本理论

对于土体来说，其组成部分分别为固体颗粒、土骨架间隙中孔隙水和空气。在有外力作用时，外力分为两部分被土体承担，一部分由固体颗粒组成的土骨架承担，并且通过颗粒之间的接触进行传递，这一部分的力称为有效应力。另一部分由孔隙水来承担，在孔隙中的水承担了法向应力，这一部分的力称为孔隙水压力，孔隙水压力的传递是通过土骨架中联通的孔隙中的水进行传递[5,6]。

1.1 基于总应力不变的有效应力分析

有效应力原理是由太沙基在1923年提出。并且在有效应力原理的基础上在1925年太沙基提出了太沙基固结理论。同时该原理有一些基本假设：1)所需计算的土体均质、各向同性、完全饱和。2)土体颗粒和水均不可压缩。3)渗流符合达西定律，渗透系数和压缩系数均为常数。4)附加应力不变，土体的总应力不变。5)只发生竖向渗流和压缩。

在实际工程中考虑基坑降水引起沉降的原理普遍认为是：随着基坑不断抽水，土层中的孔隙水压力也随之消散、转移，根据有效应力原理，总应力等于有效应力加孔隙水压力，在总应力不变的情况下，有效应力增加(增加量等于孔隙水压力的减少量)，在新增的有效应力的作用下，土体开始压缩固结[7-9]。

如图1所示，降水前，A点总应力和孔隙水压力分别为：

σ0=haγ+(hb+hc)γsat

(1)

u0=h1γw

(2)

其中，γ为土体的天然重度；γsat为土的饱和重度；γw为水的重度，kN/m3。

故降水前A点的有效应力为：

σ′=σ0-u0=haγ+(hb+hc)γsat-h1γw

(3)

降水后的A点总应力和孔隙水压力分别为：

σt=(ha+hb)γ+hcγsat

(4)

ut=h2γw

(5)

故降水后A点的有效应力为：

(6)

降水后，A点处有效应力增量：

(7)

孔隙水压力增量：

Δu=ut-u=h2γw-h1γw=-(h1-h2)γw

(8)

对于黏性土来说，γ≈γsat，所以：

Δσ′=-Δu

(9)

经过降水后，从数值上来看，土中某点的有效应力增量等于孔隙水压力减量。

1.2 基于总应力改变的有效应力分析

虽然工程上常常采用太沙基固结理论来计算沉降，但实际的有效应力和孔隙水压力的变化值并非相等的。在基坑降水过程中，总应力并非是不变的。以潜水层降水为例进行分析。如图2所示，选取A,B,C三个点分别代表在初始水位以上的点、初始水位至降水后水位之间的点、始终在水位以下的点进行讨论[10]。

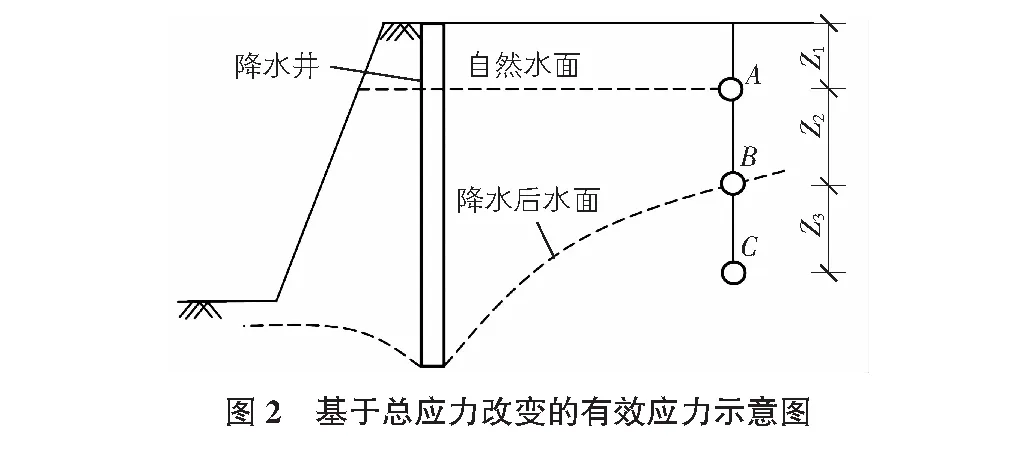
降水前A，B，C三个点的总应力、孔隙水压力、有效应力分别为：

A点：

(10)

B点：

(11)

C点：

(12)

降水到图2虚线后A,B,C三个点的总应力、孔隙水压力、有效应力分别为：

A点：

(13)

B点：

(14)

C点：

σc=σa+σb+γsatz3=γz1+γ0z2+γsatz3

uc=γwz3

(15)

其中，γ0为地下水疏干后的持水重度。

降水后三点的应力变化量见表1。

表1 降水后三点的应力变化量

对比三点降水前后的应力变化，可得出以下结论:

1)在天然水位以上的土体在基坑降水过程中的总应力、有效应力、孔隙水压力无变化。

2)在天然水位以下且在降水后降水曲线以上的土体，例如B点,总应力和孔隙水压力减少，有效应力增加。变化的值只需要确定要计算点的水位降深。当降水深度等于初始水位到降落曲线时该土体的应力变化值达到最大。

3)始终位于地下水位以下的土体，例如C点。总应力和孔隙水压力减少，有效应力增加。该区域土体各点的变化值是相等的，并且是疏干区的土体各项应力变化值的最大值。

从以上结论可以得出在总应力变化情况下潜水层降水引起的有效应力增量为：

Δσ′=(γ0-γsat+γw)z

(16)

其中，z为计算点垂直上方地下水的疏干厚度，m。

在基于总应力改变的有效应力分析降水引起的沉降时，采用的固结理论为比奥固结理论。该理论的基本假设与太沙基固结理论稍有区别：

1)孔隙水与土体颗粒均不可压缩；2)土体中渗流满足达西定律；3)变形是微小的；4)土骨架变形满足广义胡克定律，即是线弹性。

通过假定可以看出比奥固结理论没有对总应力进行假定，没有同太沙基理论假定总应力是不随着时间变化而变化。从上面的理论推导可看出，总应力在基坑降水过程中是不断变化的，因此用太沙基固结理论对实际工程进行沉降计算是不如比奥固结理论来的精准。

2 降水引起的地面沉降计算

基坑周围土体的沉降S用下式来表示：

S=Sd+Sc+Ss

(17)

其中，Sd为弹性变形或瞬时变形；Sc为固结沉降量；Ss为次固结沉降量。

基坑工程中若施工时间不长可以忽略次固结沉降量Ss。本文主要讲的是基坑降水引起的沉降，所以主要考虑固结沉降量Sc。基坑随着降水地下水位也随之下降，降水曲线上部土体有效应力的增加，使土体开始发生固结沉降，这种情况可以忽略弹性变形(瞬时变形)Sd的影响，但是如果地层中具有砂性土层时，则不能忽略弹性变形(瞬时变形)Sd。

2.1 工程中常用计算方法

目前国内对于基坑降水引起的基坑表面沉降主要依据规范[11，12]，它们都是基于分层总和法来计算降水引起的沉降。

(18)

其中，S为降水引起的地面总沉降量，m；Si为第i层计算土层的沉降量，m；Δpi为第i层计算土层由于降水引起的附加压力(有效应力的增量)，kPa；Ei为第i层计算土层的压缩模量；Hi为第i层计算土层的厚度，m。

当总应力不变的时候来计算附加压力Δpi:

Δpi=Δσ′=γw(H-y)

(19)

其中，H为降水前土层的水位高度，m；y为降水后水位的高度。

当考虑总应力改变的时候来计算附加压力Δpi:

Δpi=Δσ′=(γ0-γsat+γw)Δhw

(20)

其中，Δhw为水位降深，m；γ0为地下水疏干后的持水重度，kN/m3；γsat为土的饱和重度，kN/m3；γw为水的重度，kN/m3。

对于压缩模量Ei可以用下式计算：

(21)

其中，e0为土层的原始孔隙比；αv为土层的体积压缩系数，1/kPa。

根据裘布依假设，潜水层基坑降水后的降落曲线y由下式计算:

(22)

其中，l+h为降水井中水位高度,高度从不透水层起算(降水井为完整井时为l)，m；R为影响半径，m；r为降水井半径，m；H为潜水层厚度，m。

2.2 数值模拟计算方法

对于解析解来计算地面沉降而言，限制较多，不能充分的考虑复杂的边界条件和初始条件，假定了土体是线性、连续的，不能与实际土体的情况联系起来。采用数值模拟如有限差分法、有限元法，可以充分的考虑复杂土层在降水情况下的沉降。可以计算弹塑性问题、粘塑性问题，可以对渗流和应力进行耦合计算，可以模拟基坑降水各个工况的沉降。现在计算机的高速发展带动了数值模拟计算的发展，大型商用有限元模拟的软件如ABAQUS，FLAC3D，Midas GTS出现，对计算降水引起的沉降带来更多的便利13-15。

3 基于能量损失率最小原理求降落曲线

以上分析了基坑降水引起的地面沉降的机理，并介绍了计算地面沉降的方法。虽然在计算附加应力时，多方面分析了土体应力的变化，考虑了疏干区和降水饱和区的应力变化，使得计算结果更加准确。但降水引起的地下水位的变化没有详细的讨论。

降落曲线的计算方法除了文中所提到的，还有标准曲线对比法、图解法、试验法、切线法等。这里重点讲一下基于能量损失率最小原理求解降落曲线的有限单元法，该方法具有计算精度高、易收敛的特点。

基坑降水形成的降落曲线将土体分成两大部分，曲线以上为渗流虚域，以下为渗流实域。对土体进行有限的单元划分，根据单元所处的位置不同将单位分成实域单元、虚域单元、过渡单元。要求降落曲线，就要知道每一个真实的溢出点。当计算时设的溢出点低于实际的溢出点时，则部分的真实的溢出段就会被定义为不透水边界，这就会阻止这部分真实溢出段势能的流失，使得全域总水头高于实际，导致此时全域总势能高于实际值；当计算时设的溢出点高于实际的溢出点时，使得不透水边界变成了透水边界，增加了边界上的水头，进而使得此时全域总势能高于实际值。因此无论假设的溢出点高于或低于真实的溢出点，全域总势能都比真实值要高，并且随着假设的溢出点的升高，全域总势能呈现先减小后增大的变化过程[16,17]。定义每延米的单元总势能为:

(23)

其中，Ee为每延米的单元总势能，J/m;ρ为水的密度；g为重力加速度；Ni为单元形函数；n为单元节点数。

4 结语

本文主要阐述了潜水层基坑降水过程中引起的地面沉降的主要机理，并对引起地面沉降的附加应力和水头的变化值分别进行讨论。总结归纳了工程常用的降水引起的地面沉降计算方法、土的附加应力计算方法、降落曲线的算法。经过分析太沙基固结理论虽然对一维的沉降计算较为准确，但是忽视了降水过程中土体的总应力也是变化的，与实际情况不符，在指导实际工程中会存在一定误差。比奥固结理论是基于总应力变化对基坑降水作用下的有效应力进行了分析，与实际情况相符，但计算过程复杂。基于能量损失率最小原理求解降落曲线，通过对土体的有限单元划分，充分考虑了复杂的边界条件，具有计算精度高、收敛速度快的优点。