关于充分统计量相关理论的一点补充
贾俊霞,刘 淼
(伊犁师范大学 数学与统计学院,新疆 伊宁 835000)
0 引言
在解决一个具体问题时,往往需要对样本进行“加工”和“提炼”,针对不同的问题构造出样本的某种函数,为此,引进统计量的概念[1].由于样本中所包含的关于总体分布的信息可分为两部分:一部分是关于总体的结构信息;另一部分是关于总体的未知参数信息.在用统计量代替样本作统计推断时,样本中所含的信息可能有所损失,为了便于推断总体的未知参数信息且保证能将样本中的未知参数信息全部提炼出来,需要一个“不损失信息”的统计量,充分统计量由此诞生,它是英国著名统计学家费希尔(R.A.Fisher)在1922年提出,并在后续MIMO雷达检测性能[2]、假设检验、最小方差无偏估计、最大似然估计、区间估计[3]等方面研究中起到了重要的作用.此外,把愈“精”愈“好”的充分统计量称之为最小充分统计量[4].
基于此,本文将运用因子分解定理和条件分布的理论知识,通过推理得到证明充分统计量更加便捷的方法[5],并对最小充分统计量的相关结果加以补充.
1 预备知识
定义1设(X1,X2,X3,…,Xn)为总体X的一个样本,若f(X1,X2,X3,…,Xn)为一个函数,且在f中不含任何有关总体分布的未知参数,则称f(X1,X2,X3,…,Xn)为一个统计量[1].
定义2[1]设(X1,X2,X3,…,Xn)是来自总体X具有分布函数F(x,θ)的一个样本,T=T(X1,X2,X3,…,Xn)为一个(一维或多维)统计量,当给定T=t时,若样本(X1,X2,X3,…,Xn)的条件分布(离散总体为条件概率,连续总体为条件密度)与参数θ无关,则称T是θ的充分统计量.

引理1(因子分解定理)[1]设连续型随机变量X,总体的分布密度为f(x,θ),(X1,X2,X3,…,Xn)是样本,T(X1,X2,X3,…,Xn)是一个统计量,则T为θ的充分统计量的充要条件是:样本函数的联合分布密度函数可以分解为
h(x1,x2,…,xn)g(T(x1,x2,…,xn),θ),
其中:h是(x1,x2,x3,…,xn)的非负函数且与θ无关;g仅通过T依赖于(x1,x2,x3,…,xn).
离散型随机变量的因子分解法情况类似[7].
引理2(最小充分统计量的存在定理)假定分解定理中的条件成立,且样本空间为欧氏的,则最小充分统计量必存在[6].
2 主要结果
定理1对于离散型随机变量X,若X的分布律为
P{X=x(i)}=p(xi,θ)(i=1,2,…),
(X1,X2,X3,…,Xn)是一样本,T(X1,X2,X3,…,Xn)是一个统计量,对于任意的未知参数θ和任意的一组样本观测值,当
(x1,x2,…,xn)∈T′(t)=
{(x1,x2,…,xn)|T(x1,x2,…,xn)=t}
时,有
P{X1=x1,X2=x2,…,Xn=xn,T=t,θ}=
P{X1=x1,X2=x2,…,Xn=xn,θ}.
证明若
T′(t)=
{(x1,x2,…,xn)|T(x1,x2,…,xn)=t},
有一组观测值(x1,x2,…,xn)∈T′(t),则有
T′(t)=
{T=t}⊃{X1=x1,X2=x2,…,Xn=xn}.
于是
{X1=x1,X2=x2,…,Xn=xn,T=t}=
{X1=x1,X2=x2,…,Xn=xn}∩{T=t}=
{X1=x1,X2=x2,…,Xn=xn},
所以
P{X1=x1,X2=x2,…,Xn=xn,T=t,θ}=
P{X1=x1,X2=x2,…,Xn=xn,θ}.
定理2对于连续型随机变量X,设总体X分布密度为f(x,θ),(X1,X2,X3,…,Xn)是样本,T(X1,X2,X3,…,Xn)是一个统计量,对于任意的未知参数θ和任意的一组样本观测值,当
(x1,x2,…,xn)∈T′(t)=
{(x1,x2,…,xn)|T(x1,x2,…,xn)=t}
时,有
f(x1,x2,…,xn,θ|T=t)=
证明若
T′(t)=
{(x1,x2,…,xn)|T(x1,x2,…,xn)=t},
有一组观测值(x1,x2,…,xn)∈T′(t),则有
T′(t)={T=t}⊃{x1,x2,…,xn}.
于是
{x1,x2,…,xn,T=t}=
{x1,x2,…,xn}∩{T=t}={x1,x2,…,xn},
所以
f(x1,x2,…,xn,θ|T=t)=

证明由于X的概率密度函数为
则(X1,X2,X3,…,Xn)的联合分布密度为
L(x1,x2,x3,…,xn,θ)=
h(x1,x2,…,xn)g(T(x1,x2,…,xn),θ),

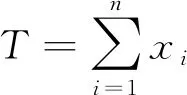
证明(X1,X2,X3,…,Xn)的条件概率为
P{X1=x1,X2=x2,…,Xn=xn,
T=t,p|T=t}=

例3设(X1,X2,X3,…,Xn)是来自正态总体N(θ,1)的一个样本,则
是未知参数θ的充分统计量.
证明(X1,X2,X3,…,Xn)的条件密度为
f(x1,x2,…,xn,θ|T=t)=
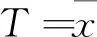
定理3设T=T(X1,X2,X3,…,Xn)是θ的一个充分统计量,s(t)是单值可逆函数,则s(T)也是θ的充分统计量.
证明下面以连续型随机变量为例进行证明,对于离散型随机变量的结果用类似方法可得.
h(x1,x2,…,xn)g(T(x1,x2,…,xn),θ)=
h(x1,x2,…,xn)g(s-1(s(T(x1,x2,…,xn))),θ)=
h(x1,x2,…,xn)q(s(x1,x2,…,xn),θ).
由因子分解定理可知,s(x1,x2,…,xn)是θ的充分统计量.由此可知一个总体的参数θ的充分统计量不唯一.
定理4设X为总体分布为f(x,θ)的随机变量,(X1,X2,X3,…,Xn)为一样本,T(X1,X2,X3,…,Xn)为一个统计量,若
(1)L(x1,x2,…,xn,θ)=
g(T(x1,x2,…,xn),θ);
(2)对一切θ∈Θ,T(x)=T(y),当且仅当fx(θ)=fy(θ),且T(x)往往直接表示为x的函数,则T(x)是最小充分统计量.
证明(X1,X2,X3,…,Xn)的联合分布密度为
L(x1,x2,…,xn,θ)=
g(T(x1,x2,…,xn),θ).
(Y1,Y2,Y3,…,Yn)的联合分布密度为
h(y1,y2,…,yn)g(T(y1,y2,…,yn),θ).
由于g仅通过T分别依赖于(x1,x2,…,xn)与(y1,y2,…,yn),对一切θ∈Θ,若T(x)=T(y),可得g(T(x1,x2,…,xn),θ)=g(T(y1,y2,…,yn),θ),h是非负函数且与θ无关,由此可知fx(θ)=fy(θ);若fx(θ)=fy(θ),则T(x)=T(y)显然成立,故T(x)是最小充分统计量.
例4设(X1,X2,X3,…,Xn)是来自正态总体N(μ,σ2)的一个样本,参数为θ=(μ,σ2),对βn上的L测度μ,T(x)是一个最小充分统计量.
证明由于X的概率密度函数为
则(X1,X2,X3,…,Xn)的联合分布密度为

易见,对一切θ∈Θ,若fx(θ)=fy(θ),当且仅当T(x)=T(y),故T(x)是一个最小充分统计量.

