高地应力软岩隧洞开挖扰动特征与规律研究

职承杰 李建贺 张传健

摘要：高地应力软岩隧洞由于地应力高，软岩强度及变形模量低，变形和破坏现象十分突出。以滇中引水工程香炉山隧洞为依托，研究了不同洞室形状和地应力场条件下，高地应力软岩隧洞围岩的变形和破坏特征。研究表明：隧洞开挖后，围岩应力、变形、破裂范围及支护结构受力均呈分区分布特征，大主应力传递轮廓和围岩变形轮廓基本呈垂直关系。对于高地应力软岩隧洞，“谐洞”并不是合理的洞形，“谐洞”虽然使切向应力在洞室边界上均匀分布，但切向应力向围岩内部的衰减速率沿短半轴方向（大曲率半径）较沿长半轴方向（小曲率半径）要小得多，导致软岩隧洞在高地应力条件下破裂范围更大;与此理念相反，通过在小主应力方向上设置小曲率半径，可更快形成高围压抑制围岩剪切破裂的进一步发展，减少围岩的破裂范围和变形程度。

关键词：软岩隧洞开挖;破裂范围;围岩变形;洞室形状;香炉山隧洞;滇中引水工程

中图法分类号：TV554文献标志码：ADOI：10.15974/j.cnki.slsdkb.2021.03.006

文章编号：1006 - 0081（2021）03 - 0034 - 08

隧洞开挖会打破岩体系统原有平衡，扰动周边围岩，使其应力场发生改变，并产生位移、破裂和失稳[1]。围岩开挖扰动的影响因素较多，一般可分为两类：一类是地质因素，包括原岩应力场、岩体结构、岩石组成及其物理化学性质等;另一类是工程因素，包括开挖方式、支护时机、隧洞形状和轴比、支护刚度等。前人在围岩扰动特征及损伤范围方面做了大量的研究工作，研究热点集中在：隧洞开挖扰动特征与损伤演化[2-3]、开挖扰动范围与原位测试[4-5]、开挖扰动区内围岩力学性质的改变[6-7]等。上述研究为认识隧洞开挖扰动特征与规律奠定了良好的基础。但由于高地应力软岩隧洞变形破坏规律复杂，且受多种影响因素制约，其开挖扰动特征与规律仍有待进一步研究。

洞室开挖形状对诱发应力及围岩扰动有直接影响。在这方面，于学馥[8]提出“轴变论”概念，认为椭圆洞室轴比对围岩变形和破裂起控制作用，当椭圆长轴与原位应力场最大主应力方向一致，并满足等应力轴比条件时，洞室周边均匀受压;如果椭圆长轴不能与最大主应力方向完全一致，可以退而求次，即确定无拉应力轴比，轴变论适合对某一既定应力场调整开挖体的形状。Richards等[9]也曾讨论过该问题，称洞周应力均匀分布的开挖体形状为“谐洞”。加拿大地下试验室（URL）在洞室形状与围岩扰动方面进行了大量的研究[7，10]，通过在ESS（Excavation Stability Study）试验洞群开挖10个不同几何断面和方位的洞室，并进行原位试验与数值分析，Read等[7]认为椭圆长轴平行于最大主应力方向较平行于水平方向时更加稳定（较小的压应力集中），且椭圆轴比越接近原位应力比时，围岩越稳定，这表明轴变论或“谐洞”的理念对于围岩条件较好（边界应力强度比相对较低）的洞室断面设计具有一定的指导作用。

但对于高地应力软岩隧洞，“谐洞”是否是最佳的洞室形状呢？虽然“谐洞”使切向应力在洞室边界上保持为常数，但是切向应力向围岩内部的衰减速率沿大曲率半径方向比沿小曲率半径方向要小得多，从应变能累积角度考虑，“谐洞”作为开挖体形状可能得不到最稳定的条件。鉴于此，本文以滇中引水工程香炉山深埋软岩隧洞为依托，对不同地应力场和不同洞室形状下围岩的变形和破坏特征进行进一步探讨。

1 工程背景及算例分析

滇中引水工程是国务院确定的172项节水供水重大水利工程中的标志性工程，其输水总干渠长度664 km，其中隧洞长度612 km。隧洞沿线地质条件十分复杂，面临着高地应力、高外水压力、突水突泥、软岩大变形、穿区域性活动断裂等重大工程地质问题，工程规模和工程技术难度均居世界前列。滇中引水工程香炉山隧洞地质剖面见图1。

滇中引水工程输水隧洞穿越以软岩为主的洞段累计长度达208.3 km，占隧洞总长的35%，经预测，可能产生软岩大变形的洞段累计长度约为88.85 km，尤以香炉山隧洞高地应力软岩大变形问题最为严峻。软岩大变形给深埋长大隧洞工程的建设及运行提出了极具挑战性的技术难题。

本文以滇中引水工程香炉山隧洞软岩洞段为例，分析隧洞的开挖扰动规律。计算洞段埋深600 m，隧洞的开挖半径为4.9 m，初始地应力场见表1，围岩力学参数见表2，支护结构参数见图2。

基于上述岩体力学参数、地应力场和支护结构参数，采用Phase2软件进行计算分析，计算结果如图3～6所示。

从图3～6可以看出，隧洞开挖后，洞周围岩最大变形为97.5 mm，发生在隧洞边墙中部;塑性区以剪切破裂为主，深度3.5～4.5 m。洞周围岩第一主应力较大值（即压应力较大值）出现在两侧边墙塑性区与弹性区交界部位，量值为-24.0 MPa，距临空面约5 m。临空面附近浅表层围岩的第一主应力量值相对 较小，压应力一般在-10 MPa以内。洞周围岩第三主应力分布规律则是距临空面越近，量值越小，开挖面附近浅表层围岩第三主應力量值在

-2.5 MPa左右，基本没有出现拉应力区。初期支护中，锚杆局部屈服，钢拱架平均应力为290 MPa，其结构内力基本在安全系数为1.4的包络线内;喷混凝土强度不足，发生破坏，洞周喷混凝土安全系数均小于1.0。

此外，从图3、4中还以发现，应力集中区沿着垂直初始大主应力的方向延展，而围岩变形区域则是沿着平行于初始大主应力的方向延展。大主应力传递轮廓和围岩变形轮廓基本呈垂直关系，表明隧洞弹性区围岩主要加载部位和主要变形部位不一致，主要加载部位（应力高度集中区）变形较小，这将在下节中进一步讨论。

2 应力场对围岩开挖扰动的影响

围岩开挖扰动的影响因素较多，如地质条件、围岩性质、地应力场、开挖方式等。限于篇幅，本文仅讨论初始应力场及洞室形状对围岩开挖扰动特征的影响。

上节算例中，初始应力场在隧洞横断面内的侧压力系数接近1（约1.1），围岩变形和破裂范围的分布特征并不明显。为更好研究这个问题，以上节算例为基础，计算以下几种工况（侧应力系数λ=0.5，1.0，2.0，2.5）。为便于总结规律，将初始应力场考虑为水平向和竖直向，不同应力场下围岩应力及塑性区如图7～10所示。

根据计算结果可以看出，随初始应力的不同，围岩扰动应力场表现为显著的分区特征，λ>1时，大主应力集中区域主要位于顶拱和底拱;λ<1时，应力集中区主要位于两侧边墙，其分布规律可以总结为：垂直于初始大主应力方向围岩应力集中，平行于初始大主应力方向围岩应力卸荷。随侧压力系数λ逐步增大，顶拱和底拱部位从卸荷状态逐步过渡为应力集中状态，且应力集中区域不断扩大。

围岩塑性区形态随侧压力系数λ不同而有明显变化。当λ=0.5时，塑性区主要位于隧洞边墙两侧，呈镰刀形;λ=1.0时，塑性区围绕隧洞成环形分布;λ=2.0时，塑性区范围迁移到隧洞顶拱和底拱;λ=2.5时，塑性区呈X形分布，沿45°方向斜伸到围岩深部。因此，围岩的剪切破坏，一般从平行于初始大主应力方向的洞壁开始，并延展到扰动应力集中区的边界;且沿着垂直初始大主应力方向破裂范围较大，平行于初始大主应力方向破裂范围较小。

不同初始应力场下围岩位移及支护结构受力如图11～14所示，图中位移单位为m，锚杆轴力单位为MN。

从图11～14可以得出，围岩变形轮廓主要沿着平行于初始大主应力的方向延展，与最大主应力传递轮廓基本呈垂直关系。隧洞弹性区围岩主要加载部位和主要变形部位不一致，主要加载部位（应力高度集中区）变形较小，而卸荷区域变形较大。对于锚杆受力，应力集中区域下部锚杆轴力较小（尽管该部位塑性区范围较大），而卸荷变形区锚杆轴力较大，锚杆轴力沿锚杆全长非均匀分布，最大轴力位于锚杆中性点处。钢拱架主要承担轴向压力，当λ=0.5时，钢拱架轴力为0.64～0.73 MN;当λ=1.0时，钢拱架轴力为0.99～1.02 MN;当λ=1.5时，钢拱架轴力为1.30～1.45 MN;侧压力系数越大，初始应力越高，钢拱架轴力则越大。

基于以上研究结论，可针对围岩不同区域进行分区调控。加载区围岩（垂直初始大主应力方向）发生剪切破裂，应力集中区向围岩深部转移，因此需注重提高该区域围岩强度（提高c，φ值）或提高支护抗力;卸荷区围岩（平行于初始大主应力方向）破裂范围较小，变形区轮廓向围岩深部延伸，应注重控制该区域围岩变形（提高围岩或支护的刚度）。图11～14中，锚杆的强度在卸荷变形区得到较大程度的发挥，而在垂直初始大主应力方向的加载部位及其下方塑性区，锚杆强度未得到有效应用，按分区调控观点，可在卸荷变形区加密布置短锚杆，加载区则可布置少量长锚杆（穿过塑性破裂区）。但需要说明的是，数值计算中对锚杆的考虑尚不全面，一般而言，配置锚杆后，不仅可以通过受拉限制围岩的径向位移（支撑作用，增加整体刚度），而且围岩强度也会有一定程度的提高（加固作用，提高c，φ值），有限元软件中的锚杆单元，通常只能反映锚杆的支撑作用，而不能反映锚杆的加固作用;本节的锚杆分区调控是从锚杆约束围岩径向位移的角度出发，而当考虑锚杆的加固作用后，则会减少加载区下方的塑性破裂范围。因此，本文提出的围岩支护分区调控只是初步设想，具体应结合工程岩体赋存条件和现场监测反馈情况开展进一步研究。

3 洞室形状对围岩开挖扰动的影响

上节讨论了不同初始应力场下，洞室围岩应力、变形和破裂的分布规律，但对于实际工程，初始应力场是客观存在的，取决于洞室埋置深度和区域构造应力的作用;而工程开挖因素则是人为的，比如隧洞轴线方位、形状、开挖规模等，工程师只能根据某一既定应力场调整洞室的形状和方位，鉴于此，本节探讨洞室形状对围岩诱发应力及变形破裂的影响。

一般而言，椭圆形是各种形状洞室应力分布及其变化规律的代表性形状，Jaeger[11]给出了椭圆洞室应力分布的解析解（弹性解），这在数值计算方法推广之前，对岩石力学的早期发展起过重要的作用。根据理论解答，当洞室断面的轴比与原位应力比相同时，那么椭圆形洞室可期望得到一个最佳的应力状态（即边界应力均匀分布），这也是轴变论[8]和“谐洞”[9]理念的基本依据。

对于中低应力场或围岩条件较好情况下（边界应力强度比相对较低），轴变论或“谐洞”的理念对洞室断面设计具有一定的指导作用。如Read等[7，10]结合加拿大地下试验室ESS试验洞群进行的相关分析，如图15所示。Read认为椭圆长轴平行于第一主应力方向较平行于水平方向更为稳定，即椭圆洞室高宽比越接近初始应力侧压比，边界上压应力集中程度越小（图15（a））。而右图洞室高宽比相对偏离初始侧压比，洞室边界最大压应力为125 MPa，超过了原位岩体强度（120 MPa），形成了V形破坏区。

但对于高地应力软岩隧洞，“谐洞”理念是否适用有待商榷。当洞室高宽比接近初始应力场的侧压比时，虽然边界切向应力集中程度有所减小，但边界高应力的范围反而加大。笔者曾在Read[7]基础上分析过不同几何断面下洞室边界的应力分布，如图16所示。

从图16中可以分析得出，随轴比逐步接近原位应力比（σ1/σ3=5.45），边界压应力集中的峰值逐渐降低，但是边界高应力的范围却逐渐加大。与此相反，轴比远离应力比，可以发现洞室邊界上的压应力集中峰值更大，但是压应力集中的范围却大幅减少。从这一点出发，有理由怀疑“谐洞”作为开挖体形状在高地应力下可能得不到最稳定的条件，尤其是对于高地应力软岩隧洞，边界上相对均匀的应力分布不能作为洞室设计的合理基础。

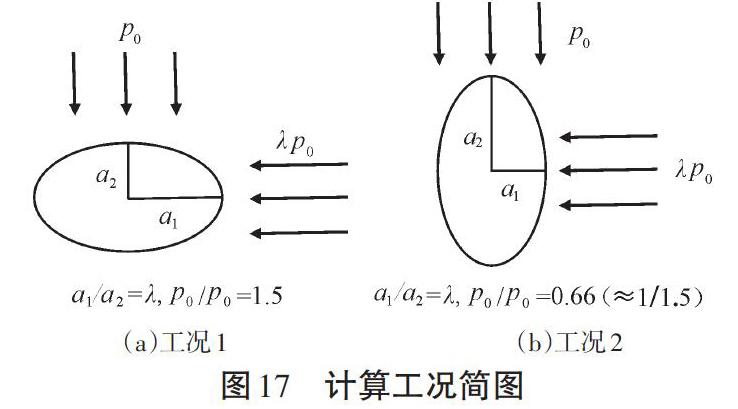
“谐洞”虽然切向应力在洞室边界上保持为常数（基于弹性解），但是切向应力向围岩内部的衰减速率沿水平轴方向（大曲率半径）较沿垂直轴方向（小曲率半径）要小得多，从应变能累积角度考虑，把洞室断面旋转90°（小曲率半径布置在小主应力方向上），有利于减少塑性破裂区范围，进而达到更好的稳定状态。为印证这一观点，以上一节高地应力软岩隧洞算例为基础，埋深600 m，侧压力系数λ取1.5。分析两种工况，工况1为“谐洞”，满足等应力轴比条件，工况2与工况1初始应力场相同，但在工况1基础上旋转90°，即把小曲率半径布置在小主应力方向上，两种工况示意图如17所示。

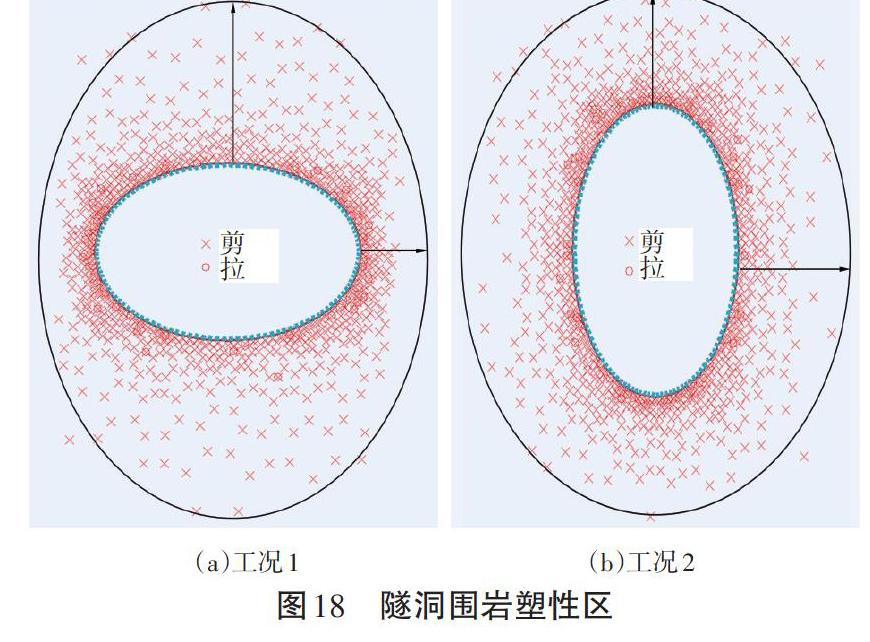
现结合Phase2有限元软件，分析两种工况下围岩应力、变形和破坏规律，围岩力学参数和支护参数同上一节，椭圆洞室长半轴取5.0 m，短半轴取3.3 m。两种工况下，围岩塑性区计算结果如图18所示。

从图18可以看出，高地应力软岩条件下，“谐洞”周边围岩塑性区分布不均，沿椭圆洞室短半轴方向塑性区厚度较大，最大塑性区半径约6.4 m;将其旋转90°后，洞周围岩塑性区相对均匀，最大塑性区半径约5.0 m。从洞周围岩破裂和稳定状态来看，后者（小曲率半径布置在小主应力方向）要比“谐洞”更为合适，“轴变论”或“谐洞”理念不适用于深埋高地应力软岩隧洞。工况1、工况2的洞周围岩应力云图如图19～22所示。

从前文分析可知，初始小主应力方向是围岩应力集中和剪切破裂产生的主要部位。从图19～22可以看出，工况1、工况2最大主应力σ1集中区域均位于初始小主应力方向上，且工况2（小曲率半径布置在小主应力方向）应力集中程度要比工况1（“谐洞”）更高;对于最小主应力σ3，均在洞室周边卸荷，只是沿初始小主应力向围岩深部延伸，工况2中σ3增长的梯度更快，其实质上反映了小曲率半径更容易使围岩形成高围压。综上可知，“谐洞”在初始小主应力方向上，围压σ3上升梯度小，进而导致剪切破裂充分发展;而在小主应力方向上设置小曲率半径（工况2），可更快形成高围压抑制剪切破裂进一步扩展，并将高压应力限制在围岩深部。

工况1、工况2的围岩位移云图如图23～24所示。

从图23～24可以得出，工況1（“谐洞”）的围岩变形要比工况2的围岩变形程度大，工况1围岩变形最大值为17.8 cm，工况2围岩变形最大值为14.5 cm。由图可见，工况1（“谐洞”）破裂范围和变形程度均比工况2（小曲率半径布置在小主应力方向）大。因此，在高地应力软岩隧洞条件下，“谐洞”并不是最合理的洞形，而通过在小主应力方向上设置小曲率半径，可更快形成高围压抑制围岩剪切破裂的进一步发展，减少围岩的破裂范围和变形程度。

4 结 论

隧洞围岩扰动应力场、变形和破裂范围研究是进行围岩稳定性评价和加固支护设计的理论基础。本文针对高地应力软岩隧洞开挖扰动特征与规律进行探讨，形成如下认识。

（1）隧洞开挖后，围岩扰动应力场和形变场呈分区分布特征。应力集中区沿着垂直初始大主应力的方向延展，而围岩变形区域则是沿着平行于初始大主应力的方向延展;大主应力传递轮廓和围岩变形轮廓基本呈垂直关系，表明隧洞弹性区围岩主要加载部位和主要变形部位不一致，主要加载部位（应力高度集中区）变形较小，而卸荷区域变形较大。

（2）围岩的剪切破坏，一般从平行于初始大主应力方向的洞壁开始，并延展到扰动应力集中区的边界;且沿着垂直于初始大主应力方向的破裂范围较大，平行于初始大主应力方向的破裂范围较小。对于锚杆受力，应力集中区下部锚杆轴力较小（尽管该部位塑性区范围较大），而卸荷变形区锚杆轴力较大，因此，可根据围岩和支护结构受力对隧洞围岩进行分区域调控。

（3）对于高地应力软岩，“谐洞”并不是合理的洞形。“谐洞”理念源于椭圆洞室理论解，可使切向应力在洞室边界上均匀分布，但切向应力向围岩内部的衰减速率沿短半轴方向（大的曲率半径）较沿长半轴方向（小的曲率半径）要小得多，导致软岩隧洞在高地应力条件下破裂范围更大;与此理念相反，通过在小主应力方向上设置小曲率半径，可更快形成高围压抑制围岩剪切破裂的进一步发展，减少围岩的破裂范围和变形程度。

参考文献：

[1] 钮新强，张传健. 复杂地质条件下跨流域调水超长深埋隧洞建设需研究的关键技术问题[J]. 隧道建设（中英文），2019，39（4）：523-536.

[2] 李邵军， 冯夏庭， 张春生， 等.  深埋隧洞 TBM 开挖损伤区形成与演化过程的数字钻孔摄像观测与分析[J].  岩石力学与工程学报， 2010， 29（6）： 1106-1112.

[3] 邹洋，李夕兵，周子龙，等. 开挖扰动下高应力岩体的能量演化与应力重分布规律研究[J]. 岩土工程学报，2012，34（9）：1677-1684.

[4] 李占海.  深埋隧洞开挖损伤区的演化与形成机制研究[D]. 沈阳： 东北大学， 2013.

[5] B?KBLOM G， MARTIN C D. Recent experiments in hard rocks to study the excavation response： Implications for the performance of a nuclear waste geological repository[J].  Tunnelling and Underground Space Technology， 1999， 14（3）：377-394.

[6] JAKUBICK A T， FRANZ T. Vacuum testing of the permeability of the excavation damaged zone[J].  Rock Mechanics and Rock Engineering， 1993， 26（2）： 165-82.

[7] READ R S. 20 years of excavation response studies at AECLs underground research laboratory[J].  International Journal of Rock Mechanics & Mining Sciences， 2004， 8（41）： 1251-1275.

[8] 于学馥.  地下工程围岩稳定分析[M].  北京： 煤炭工业出版社， 1983.

[9] RICHARDS R， BJORKMAN G S.  Optimum shapes for unlined tunnels and cavities[J].  Engineering Geology， 1978， 12（2）： 171-179.

[10] READ R S， CHANDLER N A， DZIK E J. In situ strength criteria for tunnel design in highly-stressed rock masses[J].  International Journal of Rock Mechanics & Mining Sciences， 1998， 3（35）： 261-278.

[11] JAEGER J C， COOK N G W. Fundamentals of rock mechanics[M].  London： Chapman & Hall， 1976.

[12] 李建贺，盛谦，朱泽奇，等. 脆性岩体开挖损伤区范围与影响因素研究[J]. 岩土工程学报，2016，38（增2）：190-197.

（编辑：李 慧）