设施农业就地翻土犁结构设计与仿真*
于圣洁,刘元义,胥备,杨书搏,张悦,杨超
(山东理工大学农业工程与食品科学学院,山东淄博,255000)
0 引言
设施农业作为现代农业的重要组成部分,并随着我国农业技术的发展[1],设施农业体量已经达到世界第一,约占世界设施农业的80%[2],但是也存在诸多不足,如潮湿环境加之长期的重茬种植,导致细菌及虫卵孳生,引发严重的病虫害现象[3]。铧式犁深翻作业可有效防治病虫害[4],但铧式犁的翻垡特性导致耕作时土壤会有侧移[5],设施农业中空间较小且有立柱墙壁等障碍物的限制,难以使用普通铧式犁。所以设施农业中耕整作业大多采用旋耕法[6],其耕作深度一般不超过20 cm,难以达到深翻的目的[7]。因此,需设计一种耕作后土垡无侧移的就地翻土犁[8]。
对于“正面犁”“横排犁”等原沟翻转概念犁体,马廷玺翻译了美国专利“土垡原地翻转横排犁”[9];王梦熊翻译莫斯科哥略契金农业生产工程学院设计研制的“正面犁”[10];王世学一等设计了一种双铧对称式的犁体[11-13];佳木斯工学院尤玉锴推测土垡运动规律设计了一种螺旋式犁体曲面及一种横排犁[13]等。土壤在很大程度上影响农业机械,其物理性质的一些微小变化都将引起土壤耕作机械结构整体或部分的改变[14-15]。在设计土壤作业机械或是对现有机械进行改进时,必须重视农业机械对土壤的力学研究[16]。离散单元法模拟可以描述土壤的力学行为,李博[17]运用离散元法对深松铲进行了研究,黄玉祥等[18]基于离散元分析了深松铲的扰动行为,赵吉喆[19]采用离散元法对马铃薯挖掘铲进行了仿真试验。故运用EDEM验证犁体耕作是有必要的。
上述诸多设计方案均在一定程度解决了土垡侧翻问题,但也有各自不足,比如犁体设计制造难度高及当时没有相应的技术支持和恰当的适用场合等原因没有得到推广普及,没有形成完整的设计方法,因此有必要针对就地翻土犁进行研究。本文在上述研究的基础上,基于翻土曲元法对就地翻土犁进行正向设计,解决了原沟翻转犁的参数化设计难题,命名所设计犁体为就地翻土犁。利用EDEM离散元软件对所设计的就地翻土犁进行了仿真试验,并且对就地翻土犁的阻力进行分析。
1 就地翻犁结构设计
1.1 翻土曲元法
翻土曲元法是就地翻土犁研究的成型方法,是研究水平直元线法和翻土曲线族法所得。水平直元线法是一直元线沿导曲线按照与犁沟沟壁间的元线角的变化规律,自下而上地移动扫掠即可形成连续的犁体曲面。翻土曲线族法,是利用垂直于犁体前进方向的多个平面剖切犁体曲面,得到的交线称为翻土曲线族,通过控制每条翻土曲线参数设计不同的犁体曲面[20]。翻土曲元法结合以上两种犁体成型方法,先确定土垡经过犁体曲面实现原沟翻转路径的导曲线,再利用垂直于犁体前进路线的多组横截面得出土垡运动的曲元线族,把曲元线族通过导曲线联结起来形成面。翻土曲元法把犁体耕作时土垡实际运动轨迹与犁体曲面设计联系起来[21],属于土迹线成型犁体[22]。
1.2 就地翻土犁导曲线
导曲线即土垡横截面底边中点的运动的轨迹,如图1所示,这条曲线从犁铧末端开始依次经过犁颈、犁胸和犁翼。它的形状、长度、走势以及弯曲程度等因素和主犁体曲面的形状与耕作性能有着密切关系。
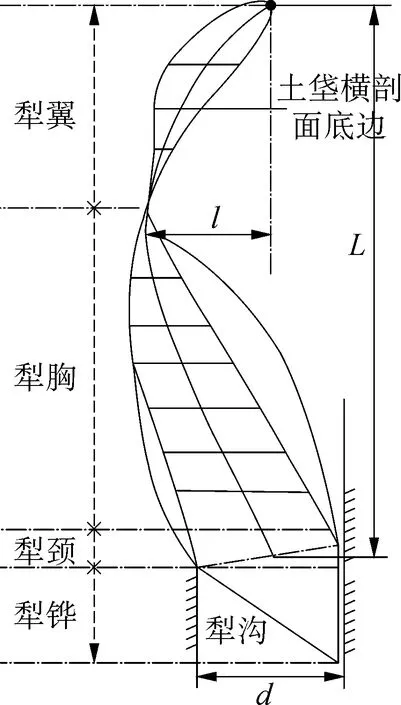
(a)xoy面俯视图
导曲线是一段空间的曲线,表示土垡由犁铧至犁翼翻转的路径。在俯视图上这段曲线由两段抛物线构成,其离犁沟中线的最远距离称为开度l,开度l影响犁胸对土垡的引导作用,l越大则引导作用越强。总长L即土垡经过犁颈、犁胸到犁翼所需要的犁体曲面的长度,设计时l与L应保证适当的比例,l/L一般取0.2~0.3,导曲线终点位于原犁沟宽中线上。正视图上该段导曲线为一抛物线,曲线最高点即为土垡翻转至90°的位置,土垡经过犁胸和犁翼时,横剖面底边均翻转了90°,但其经过犁胸从0°翻转至90°与经过犁翼从90°翻转至180°所需要的犁体长度不同。这是因为土垡在经过犁胸时,需克服重力延续土垡经过犁铧后的提升趋势,加之抬垡需要做功,所消耗的能量更大,因此犁体曲面长度更长。犁胸长度与犁翼长度的比例为1.6~2。导曲线最高点与土垡横剖面底边零度线所在点的连线与地面的夹角γ称为提升角。提升角过大则土垡需要克服的重力增大,导致耗能高,而提升角过小则在犁体工作速度快时影响犁胸对土垡的翻转效果,提升角的变化规律如式(1)所示。
(1)
式中:Δγ——提升角与地面夹角的差值;
d——犁体耕作幅宽;
L2——犁胸长度。
1.3 就地翻土犁翻土元线族
翻土元线为长度相等的多条线段,反映理想状态下的土垡在犁体各个部位的横剖底边线与地面的夹角,如图1中的土垡横剖底边线所示。犁铧切土形成土垡后,翻土元线开始沿就地翻土犁犁体曲面翻转,主要经历了三个过程,即在犁颈上翻转至水平、在犁胸上翻转侧被抬起至竖直、在犁翼上被翻转至原犁沟。θ依次经历了犁颈上(ε~0°)犁胸上(0°~90°)和犁翼上(90°~180°)三个过程,其变化规律如式(2)所示。
f(y)=-0.28y+25,y∈[0,90]
f(y)=0.3y-27,y∈(90,390]
f(y)=0.001 64y2-2.053y+640.6,
y∈(390,584]
(2)
式中:y——犁体在y方向的值。
由土垡横剖底边线与地面的夹角变化规律得到元线角θ沿y轴负方向的变化规律可如图2(a)所示。在AB段犁颈使得土垡底边线变为水平,元线角θ从ε减小至0°,这段曲线的斜率为固定值。在BC段犁胸抬起土垡割裂侧至竖直的过程,元线角θ从0°增至90°。这段曲线可以为直线,也可以为一抛物线。即曲线斜率k为固定值或为线性变化,其角度增长趋势可以为均匀增长、由慢到快或者由快到慢增长。犁胸部分的曲面长度较长,元线角度增长规律的不同对犁体翻垡效果以及所受阻力影响较大,应根据不同的设计选择合适的元线角变化规律。在CD段犁翼翻转土垡至犁沟过程,元线角θ从90°减至0°。这段曲线为一开口向上的抛物线,即曲线斜率的绝对值|k|由大变小线性减小,其元线角以由快到慢的趋势减小。这是因为土垡经过犁翼部位时,重心已经越过土垡翻转边界,土垡即将脱离主犁体曲面。越靠近犁翼尾部,犁翼对土垡的翻转作用就越小,因此应在土垡刚进入犁翼部分时就具有较大翻转力度使角度迅速减小,即较大的|k|。
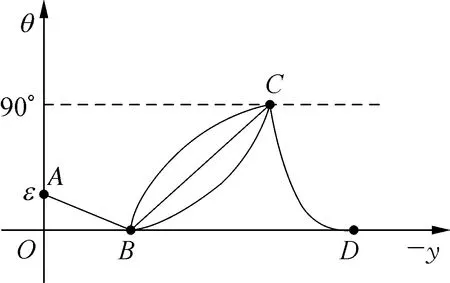
(a)元线角斜率
1.4 就地翻土犁翻土曲线族
犁铧作用土壤形成土垡后,土垡沿着犁体曲面翻转,翻土元线反映的是与地面的夹角,但真实的土垡横剖底边线并不是线段而是曲率不断变化的曲线,而反映横剖土垡底边线曲率的曲线称为翻土曲线。翻土曲线可近似的认为是抛物线,抛物线的曲率应根据土型、耕速等因素确定。如图2(b)所示,元线角的大小决定着这个翻土曲元线的斜度,其变化规律已由上述分析得知。θ1为翻土曲线在土垡铧切侧处切线与地面的夹角,θ-θ1大小则决定了翻土曲线铧切侧的斜率。θ-θ1的变化规律如式(3)所示。
f(y)=0.777 8y,y∈[0,90]
f(y)=-0.000 882y2+0.5y-30.86,
y∈(90,390]
f(y)=-0.154 6y+90.31,y∈(390,584]
(3)
θ2为翻土曲线在土垡翻转侧处切线与地面的夹角,其大小决定了翻土曲线翻转侧的斜率。θ2-θ的大小则直观的反映了翻土曲线的弯曲程度以及其具体形状,θ2-θ的变化规律如式(4)所示。
f(y)=0.111 1y,y∈[0,90]
f(y)=-0.000 577 5y2+0.307 9y-13.03,
y∈(90,390]
f(y)=-0.098 97y+57.8,y∈(390,584]
(4)
分析θ2-θ的变化规律即可得到翻土曲线变化规律,进而得到所需的犁体曲面。
2 离散元法仿真分析
2.1 土壤颗粒模型建立
颗粒模型参数的选取要接近于土壤的现实情况,这是保证仿真分析有效性的必要条件。故要依据现有的土壤物理性质研究成果,建立接近于实际情况的土壤颗粒模型。农艺标准中,2~3 mm直径的团粒被认为是理想的,不过大一点或者是小一点的团聚体(1~10 m)也是好的[23]。本文所用土壤的各个物理指标决定了土壤的类型,经查阅文献[24]得出鲁中地区的土壤的类型为壤土。以此翻阅相关文献[25-27],得到前处理所需的壤土的泊松比0.3、土壤密度2 650 km/m2、土壤剪切模量1 MPa、土壤颗粒间的碰撞恢复系数0.6,土壤颗粒间的静摩擦系数0.33、土壤颗粒的动摩擦系数0.14。
接触模型的分析计算直接决定了粒子所受的力和力矩的大小。对于不同的仿真对象,必须建立不同的基础模型。Hertz-mindlin粘结接触模型此接触模型是在Hertz-mindlin无滑动接触模型的基础上对颗粒间的切向力和法向力进行了定义,使颗粒与颗粒之间相互作用,然后外界施加一个力之后颗粒间的黏结键被破坏,然后颗粒与颗粒之间作为硬球相互作用。当犁体对土壤模型作用力达到土壤颗粒间所最大法向、切向应力时土壤粘结状态被打破[28]。对于Hertz-Mindlin黏结模型下的黏结刚度参数对仿真结果的影响非常小,令法向黏结刚度等于切向黏结刚度[29],定义黏结刚度为5×107N/m3[30]。临界应力将直接关系到犁体的耕作阻力及犁体的耕翻效果,定义仿真试验的法向临界应力为3×105Pa,切向临界应力为5×105Pa[31]。土壤粘结半径定义为10 mm,建立长为2 000 mm,宽为800 mm,高为400 mm 的土壤模型,土壤颗粒堆积150 mm,经压缩后形成黏结键。
2.2 犁体建模
结合设计经验以及农业技术要求确定各个部分初始参数,再结合初始参数拟合得到翻土元线变化规律,如表1所示。

表1 犁体设计参数
利用SoildWorks软件,对犁体进行建模。在俯视图和侧视图上绘制出犁沟以及犁铧的轮廓线,确定导曲线的开度l,以及起始点终止点位置,绘制一条3D曲线,把翻土元线相交于导曲线上,进行画面填充,绘制出如图3所示的犁体曲面。最后对没有厚度的面加厚,并进行圆滑处理,得到所需的犁体模型。
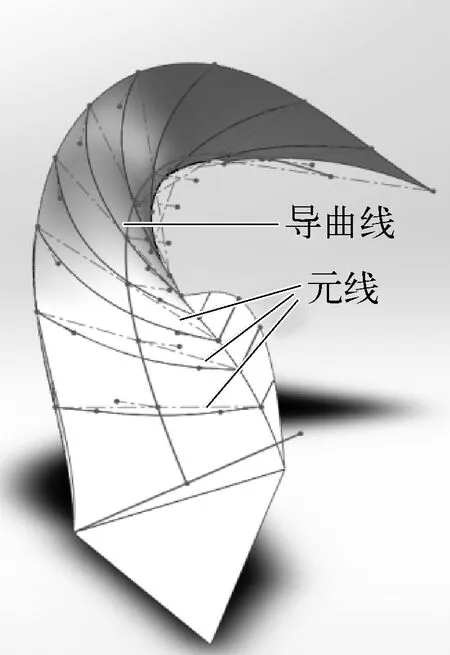
图3 犁体曲面
2.3 就地翻土犁仿真参数
要确保仿真试验的精确性,犁体模型采用1∶1的比例进行试验,采用Solisworks进行犁体建模,保存为*.STL格式。就地翻土犁的材料犁铧采用65Mn钢,其强度和刚度都能满足犁体工作要求。,松比为0.3、密度7 850 kg/m3、剪切模量7.9×1010[32],犁体与土壤的接触参数,碰撞恢复系数取0.3、犁体与土壤的静摩擦系数0.3、动摩擦系数0.2。犁切割、破碎和翻转土垡和杂草,并使土壤受压破碎,普通犁的耕作速度为4.5 ~6 km/h,当耕速超过7 km/h时,即属于高速作业[33],设置就地翻土犁运行速度为1.67 m/s。
2.4 仿真分析
犁体耕作幅宽为250 mm,耕深为150 mm,仿真在2 000 mm×800 mm×400 mm的虚拟土槽中进行,生成400 017个颗粒和198 964个bond键,时间为3 s,网格的尺寸设置为最小颗粒半径尺寸的两倍[34]。如图4所示,土壤经过耕作之后是相对平整的。
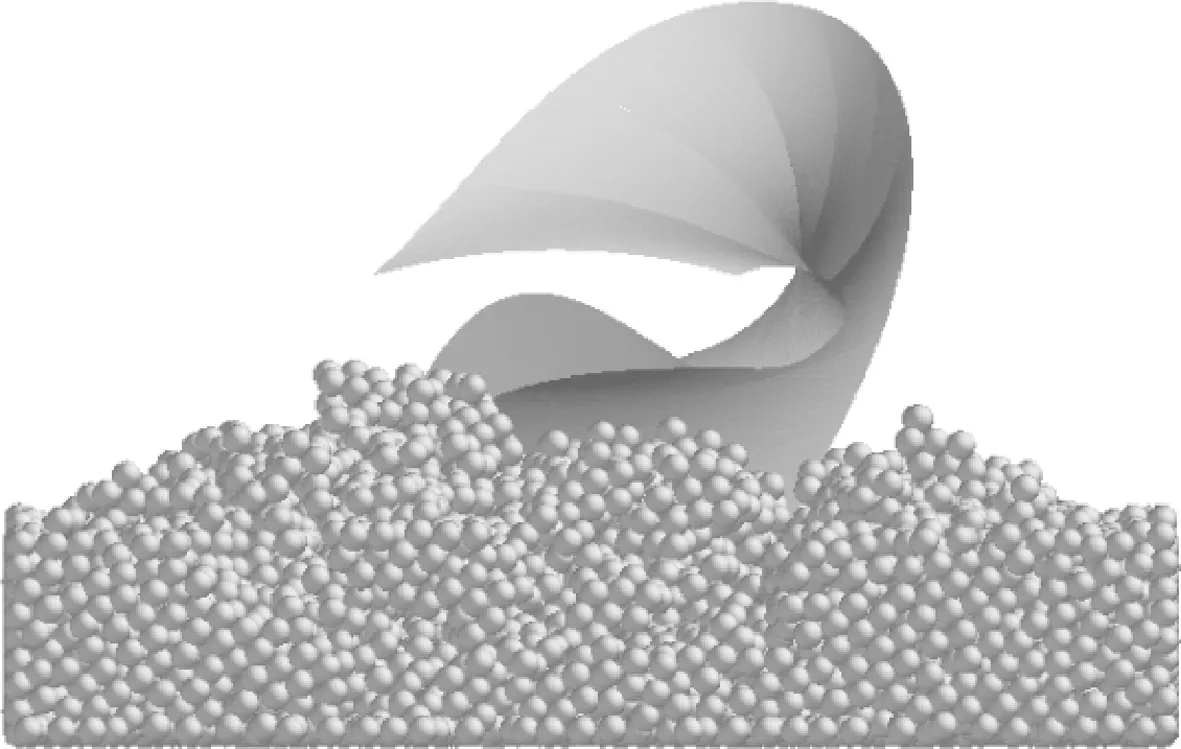
图4 犁体耕作后颗粒状态
犁体的牵引阻力是设计与研究犁体时重点的考虑因素之一,因就地翻土犁犁体曲面较为复杂,其牵引阻力变化规律也比较难以分析。经过EDEM后处理Analyst所测定的犁体曲面阻力,得到犁体阻力变化图(图5)。图中曲线所示的变化规律即为就地翻土犁在起土过程中牵引阻力的变化规律。
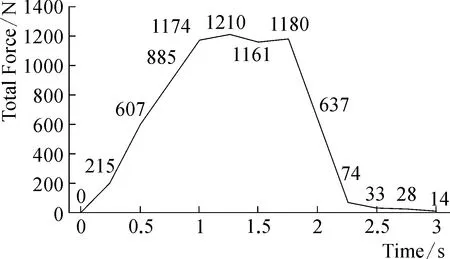
图5 犁体阻力折线图
根据此变化规律对应时刻的云图变化模拟仿真动态,可得到就地翻土犁起土过程牵引阻力变化规律:犁铧破土和土壤到达犁壁时阻力平稳增加,土壤到达犁翼时阻力达到峰值,形成土垡后牵引阻力逐渐平稳。由图5牵引阻力变化规律可以看出在土垡运动到犁颈部分时,即图中0.25 s时刻到1 s时刻,牵引阻力平稳增加。而从1 s时刻到1.75 s时刻牵引阻力达到顶峰且变化不大,由于仿真土槽只设置了2 000 mm,到达1.75 s时刻犁体已经到达土槽尽头,证明犁体的平均阻力就在1 200 N上下波动,且这一部分持续时间长,阻力持续距离也大,对整体起土阻力影响较大。
3 结论
1)基于犁体设计水平直元法和翻土曲线族法,创设了一种翻土曲元法,由翻土元线中点穿透于导曲线且翻土元线角度按照规律变化后得到一种翻垡后土垡无侧移且无犁沟的就地翻土犁体曲面,预期设计目的是可使土壤实现原沟翻转不留犁沟,可以满足设施农业中的耕作要求。
2)通过翻阅相关文献获取土壤的密度、泊松比、剪切模量、碰撞恢复系数、动摩擦系数、静摩擦系数以及犁体材料参数,采用离散元仿真软件EDEM进行就地翻土犁翻土模拟试验,研究了就地翻土犁翻土后土壤分布情况,结果表明就地翻土犁的耕作效果较好,达到预期目标,验证了设计的合理性。
3)通过对就地翻土犁的仿真试验,研究了就地翻土犁在耕作时犁体所受阻力的大小,即耕作阻力在犁铧破土和土垡到达犁壁时耕作阻力平稳上升,土壤到达犁壁端部耕作阻力达到顶峰1 200 N逐渐平稳。犁体曲面的参数决定了这一规律的变化趋势,该数据对犁体的整体设计具有较大意义。

