装甲车辆磁流变座椅振动控制方法研究

唐志勇，朱 炜，朱洪涛

(南京理工大学 发射动力学研究所， 南京 210094)

良好的作业环境是保障乘员战斗力的重要因素，而提高座椅悬架的减振性能是改善乘员的作业环境最简单有效的方法。当前座椅悬架的形式主要有三种：被动式座椅悬架、主动式座椅悬架和半主动式座椅悬架[1]。传统的被动式座椅悬架由刚度固定的弹簧和阻尼固定的阻尼器组成，它是根据特定的行驶状况进行设计的，隔振性能较差，无法适应多变的行驶路况[2]。磁流变阻尼器因其阻尼力连续可调、响应快、耗能少等优点被广泛应用于武器缓冲、军用防护、军用飞机和军用车辆等地方[3-4]。基于磁流变阻尼器的半主动座椅可以通过对磁流变阻尼器输入不同电流来调节阻尼力，从而达到更好的减振效果[5-6]。空气弹簧具有变刚度、吸振降噪性能好、重量轻、使用寿命长等特点，被应用于半主动悬架的刚度控制[7]。

<1)，且各件产品是否为不合格品相互独立．

目前大部分半主动座椅都是通过调节阻尼提高减振性能，对刚度和阻尼联合调节的研究很少。国内外学者对半主动座椅悬架阻尼调节的控制策略做了大量研究，孟小杰[8]通过遗传算法辨识得到磁流变阻尼器的模型参数，在此基础上研究了座椅悬架的开关天棚半主动控制策略；S Gad等[9]基于磁流变阻尼器设计了一种新型半主动座椅悬架分数阶PID控制器；Rajendiran S等[10]基于磁流变阻尼器设计了半主动座椅悬架PID控制器和模糊控制器，研究结果表明模糊控制器控制效果更好；Nguyen S D等[11]提出了一种新型神经模糊控制器，用于汽车驾驶员座椅磁流变减振系统；Devdutt Singh等[12]对磁流变阻尼器进行多项式建模，设计了具有耦合规则的模糊-PID混合控制器。

本文通过模糊控制策略实现了半主动座椅的刚度和阻尼联合调节，进行了随机路面下的动力学仿真，为变刚度变阻尼座椅悬架的工程应用提供了理论基础。

1 磁流变阻尼器模型建立

1.1 磁流变阻尼器的力学模型

磁流变液阻尼器在力学性能上具有强烈的非线性，而Bouc-Wen模型[13-14]是工程上广泛使用的一种阻尼器的迟滞非线性力学模型，它能够较好的体现磁流变阻尼器的迟滞现象，也能够准确的计算出阻尼器的力-位移和力-速度曲线。磁流变阻尼器的Bouc-Wen模型如图1所示。

图1 阻尼器Bouc-Wen模型示意图

阻尼力Fd为：

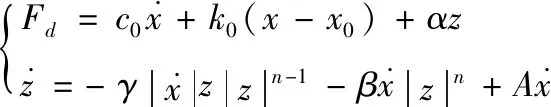
(1)

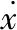
1.2 磁流变阻尼器的力学性能试验

本文针对美国Lord公司生产使用的RD-8040-1型磁流变液阻尼器进行研究，使用W+B(Walter+Bai)力学性能试验机对阻尼器进行力学性能实验，获得了正弦激励下，不同电流时阻尼器的力-位移曲线。

如图2所示利用夹具将磁流变阻尼器固定于W+B疲劳试验机上，直流电流源对阻尼器供电，施加电流分别为0 A、0.2 A、0.4 A、0.6 A、0.8 A、1 A，控制电脑使W+B试验机产生正弦激励，频率为2 Hz，振幅为10 mm，试验采样频率为1 000。

图2 磁流变阻尼器力学性能试验现场

通过改变W+B试验机的激励和磁流变阻尼器的控制电流，得到多组阻尼力和位移的数据，使用MATLAB进行数据处理，得到如图3所示的10 mm 2 Hz激励下磁流变阻尼器的力-位移曲线。

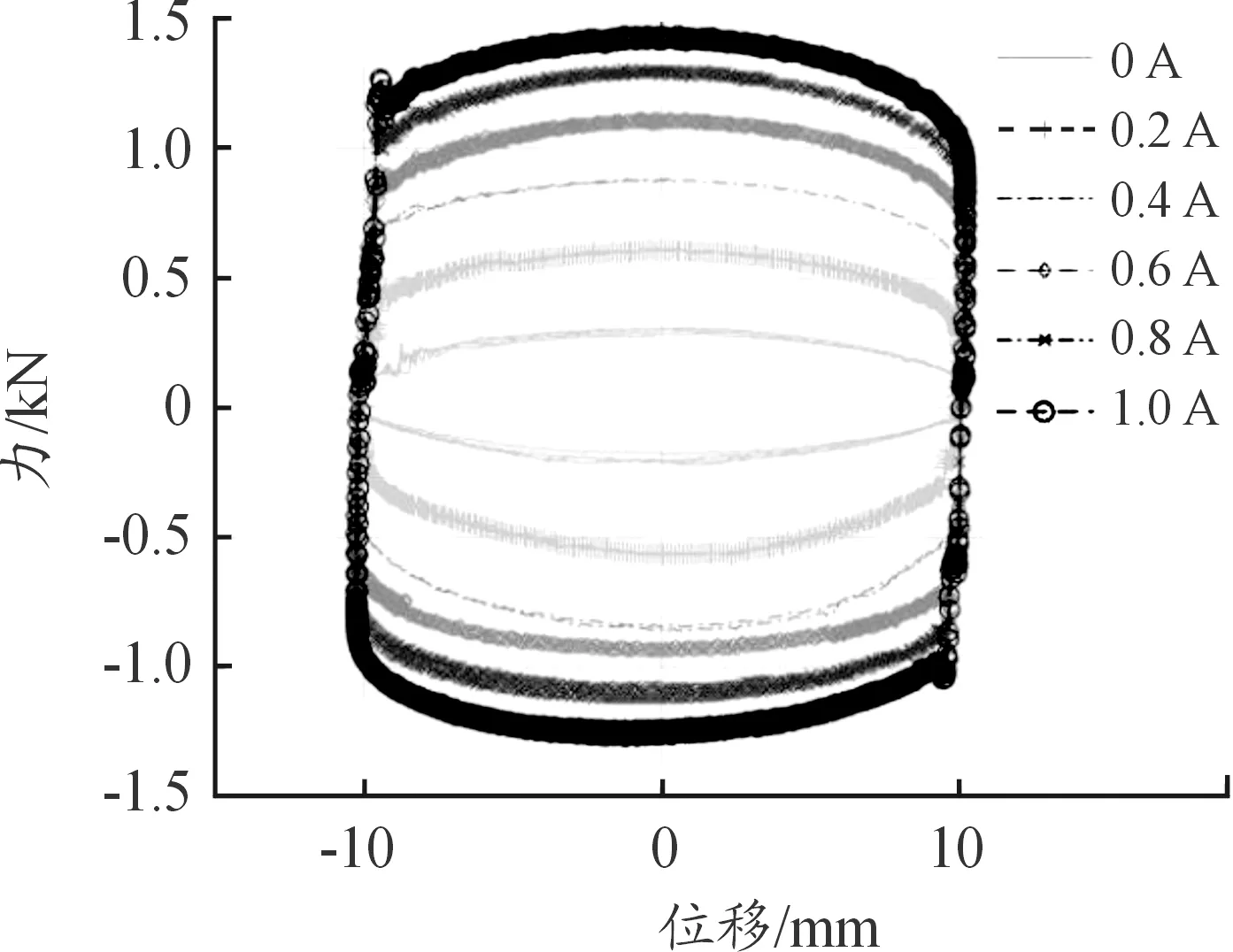
图3 阻尼器力-位移曲线

1.3 Bouc-Wen模型参数识别

为了使基于Bouc-Wen模型的计算结果吻合于实验的结果，本文选用遗传算法进行参数识别。利用Matlab中自带的遗传算法工具箱进行遗传算法的参数识别，参数拟合结果为式(2)。

(2)

式中，I为磁流变阻尼器的输入电流。

对10 mm 2 Hz激励下阻尼器数据进行拟合，电流分别为0 A、0.2 A、0.4 A、0.6 A、0.8 A、1 A，图4是磁流变阻尼器实验数据与拟合数据曲线。从图中可看出，遗传算法识别参数拟合出的红色虚线与实验得到黑色实线基本吻合，所以该Bouc-Wen模型可以真实的反映磁流变阻尼器实际出力情况。

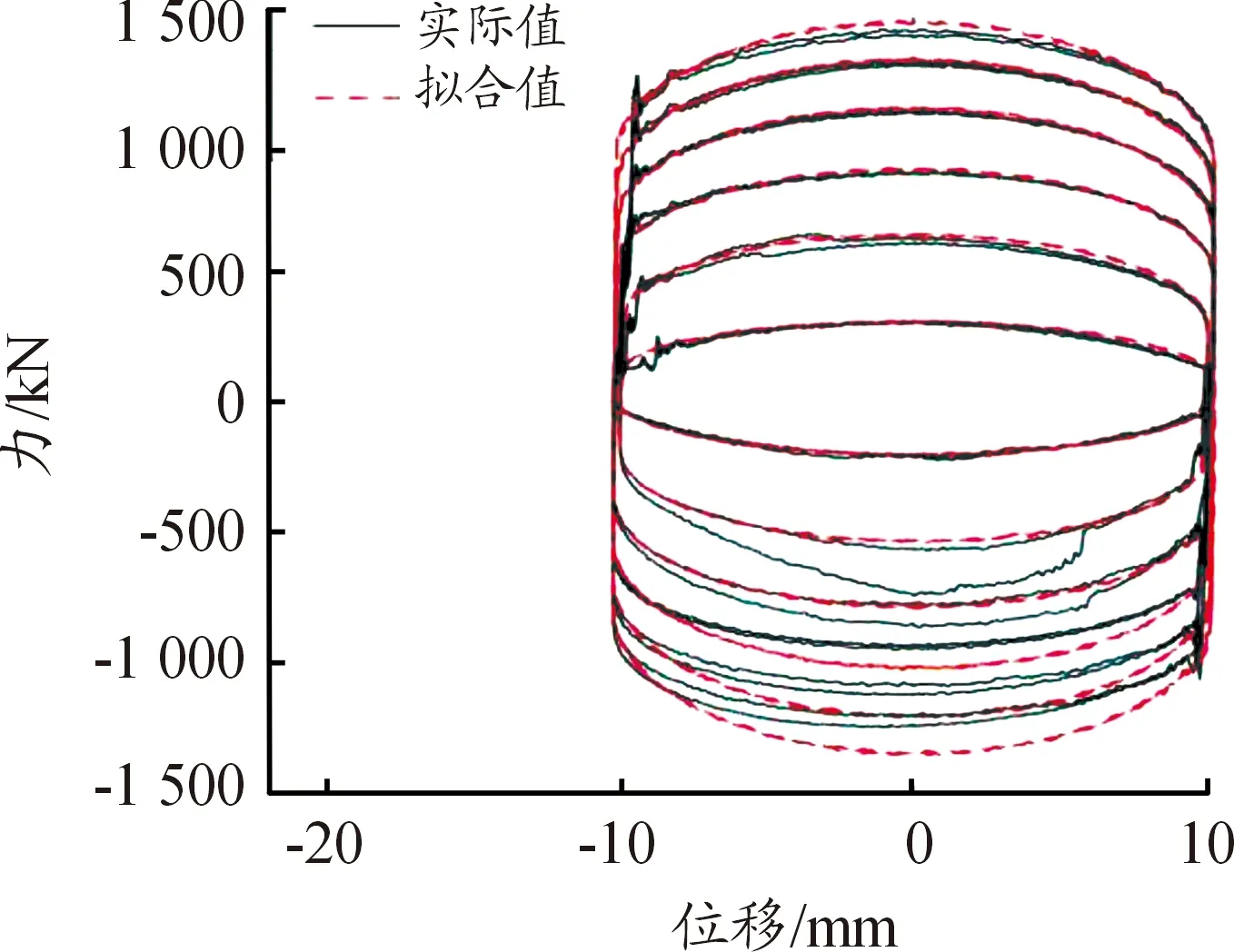
图4 磁流变阻尼器力-位移拟合数据曲线与实验数据曲线

2 座椅悬架系统分析

2.1 座椅悬架模型

装甲车辆行驶时，路面激励经过履带轮、车体最终传递给座椅和人体，假设车体是前一个振动环节，“座椅—人体”系统是后一个振动环节，这里“座椅—人体”系统的质量远小于装甲车辆车体的质量，汽车理论认为这两个环节之间没有反馈，车身底板的垂直振动就是“座椅—人体”系统的输入。利用发射动力学研究所开发的坦克动态系统仿真软件MSTMMSim(如图5所示)得到了C级路面激励下，车速10 m/s时某型装甲车车体的位移响应，如图6所示，以此作为座椅的激励。

图5 MSTMMSim软件坦克车辆动力学计算结果动画截图

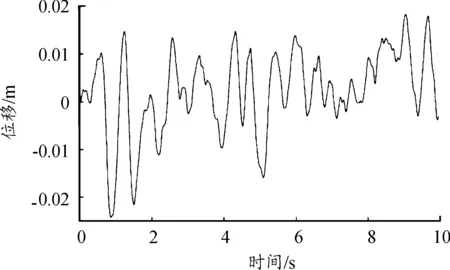
图6 C级路面下车身响应曲线

某型号座椅悬架总成如图7(a)所示，把人体简化为一个刚性质量m3，它与空气弹簧k和磁流变阻尼器Fd构成了如图7(b)所示的一自由度非线性系统。

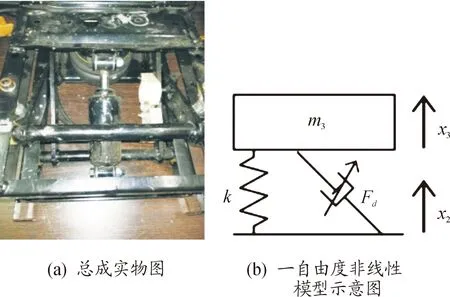
图7 座椅悬架

该模型运动方程如下：

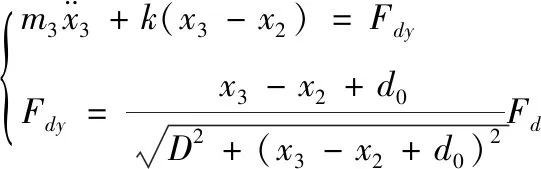
(3)

式中：m3为座椅悬架簧载质量，为80 kg；k为座椅悬架等效刚度，其值如式(4)所示；x3为座椅悬架上底板位移；x2为座椅悬架下底板位移；Fdy为磁流变阻尼器等效阻尼力；Fd为磁流变阻尼器阻尼力；D为阻尼器安装端点横向距离，为0.16 m；d0为座椅悬架上底板与下底板之间初始距离，为0.095 m。

当负载为80 kg时，对座椅悬架等效刚度和座椅上底板高度关系曲线进行拟合得到

k=1.534×108h3-2.967×107h2+

2.121×106h-4.237×104

(4)

2.2 座椅悬架振动特性

为了了解座椅悬架参数对座椅减振性能的影响，这里通过分析求解得到的“座椅—人体”加速度对激励x2的幅频特性曲线。

由式(3)可知座椅系统的幅频特性为

(5)

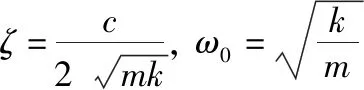
“座椅—人体”加速度对激励的幅频特性为

(6)

根据式(6)得到了图8所示的刚度和阻尼对幅频特性的影响曲线，当阻尼不变时，座椅的加速度幅频特性曲线如图8(a)所示，从图8(a)中可以看出同一激励频率下，随着刚度k的减小，加速度与位移激励的比值在减小，即加速度响应在减小，适当降低刚度可以提高座椅减振性能；当刚度不变时，座椅的加速度幅频特性曲线如图8(b)所示，从图中可以看出随着阻尼c的增大，加速度与位移激励比值的峰值急剧减小，增大阻尼可以有效减小共振，在低频时增大阻尼，高频时减小阻尼可以提高座椅减振性能。

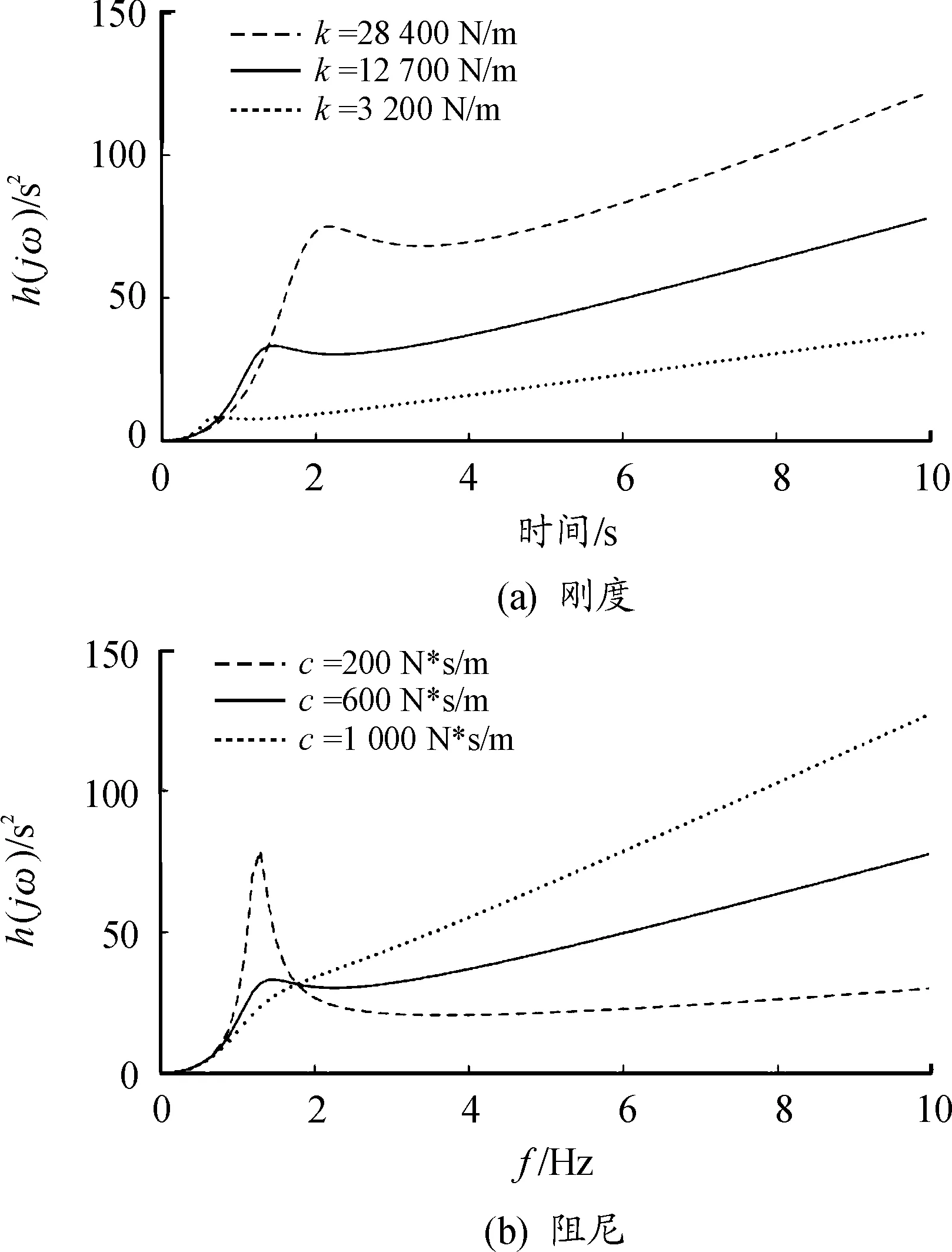
图8 刚度和阻尼对幅频特性的影响曲线

3 模糊控制及仿真

本文采用模糊控制算法来对座椅悬架进行控制，通过空气弹簧实现刚度调节，通过磁流变阻尼器实现阻尼调节，座椅悬架控制系统如图9所示。

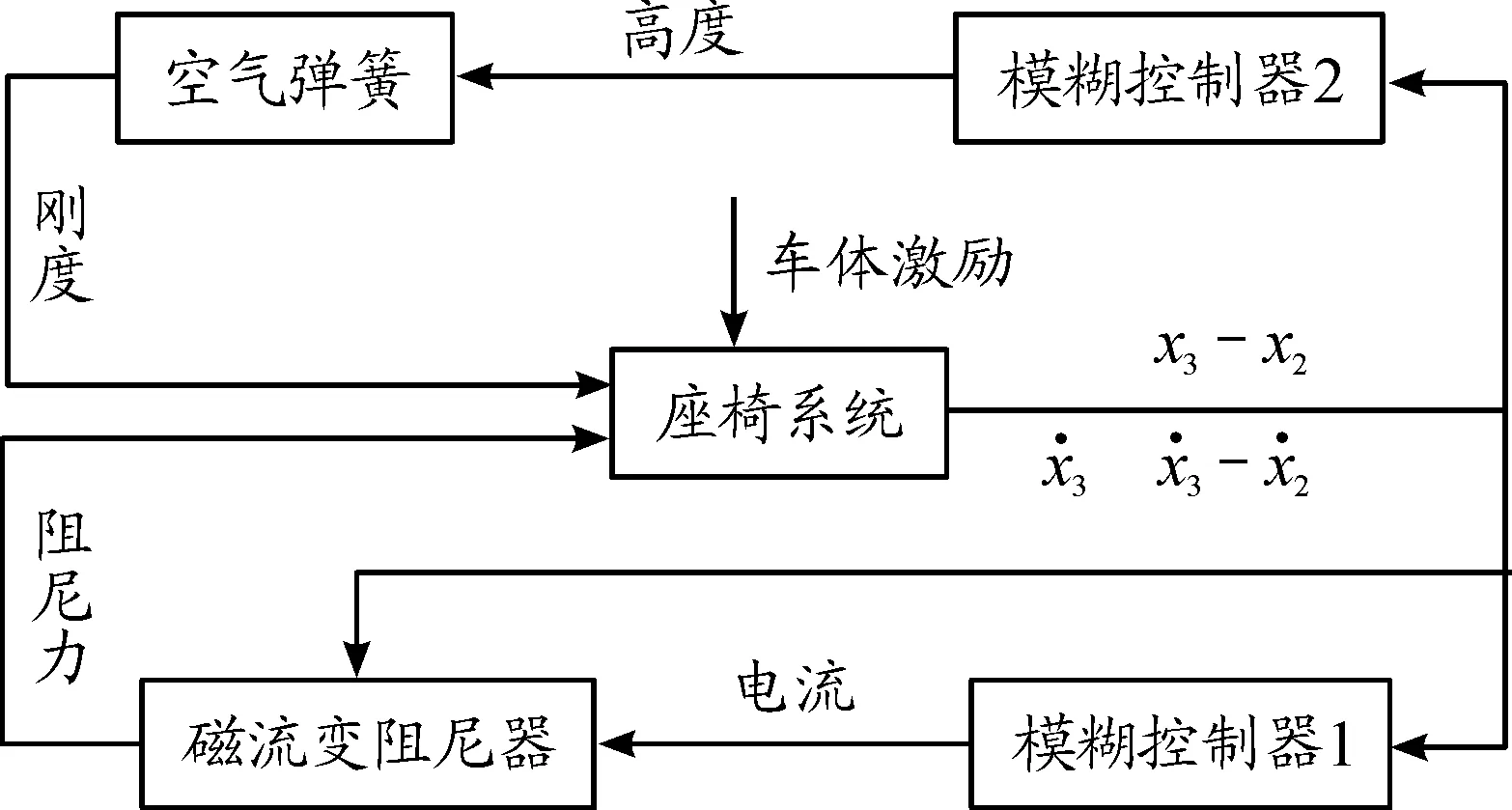
图9 半主动座椅控制系统框图

模糊控制器1的输入信号为座椅悬架上底板的速度和座椅悬架上下底板的相对速度。速度和相对速度的模糊论域为[-6，6]，量化因子kv=20，kvr=24，语言变量为“负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)”。选取磁流变阻尼器的控制电流为模糊控制器的输出，输出的范围为[0，1]，定义5个语言变量，为{S，MS，M，MB，B}，分别表示电流的小、中小、中、中大和大，输入输出变量均采用三角形隶属度函数。

模糊控制器1的控制经验如下：① 当座椅上底板速度v3和上下底板相对速度v3-v2同向时，磁流变阻尼器阻尼力应该与v3成正比，v3越大，控制电流越大；② 当座椅上底板速度v3和上下底板相对速度v3-v2反向时，磁流变阻尼器阻尼力应该为零，此时控制电流为零。根据上述经验建立的模糊控制规则如表1。

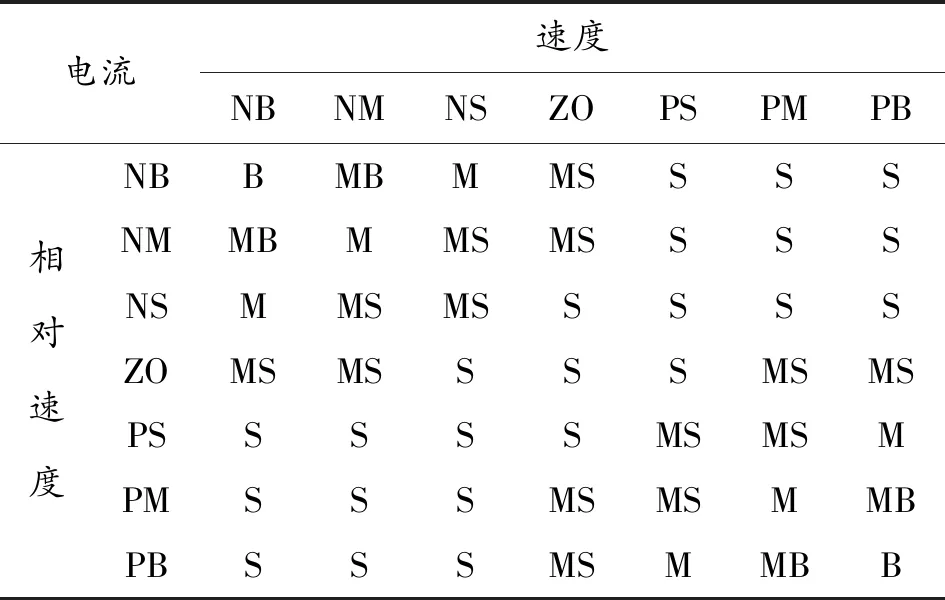
表1 模糊控制器1模糊规则

模糊控制器2的输入信号为座椅悬架上下底板的相对位移，模糊论域为[-6，6]，量化因子为200，语言变量为“负大(NB)，负中(NM)，负小(NS)，零(ZO)，正小(PS)，正中(PM)，正大(PB)”。输出信号为座椅悬架的高度，模糊论域为[0，1]，比例因子为0.1，语言变量为“大(B)，中(M)，小(S)，零(ZO)”，输入输出变量均采用三角形隶属度函数。

模糊控制器2的控制经验如下：当座椅悬架上下底板相对位移较小时，在限位行程内尽可能降低座椅高度，即对空气弹簧放气来减小座椅刚度；当座椅悬架上下底板相对位移较大时，尽可能提高座椅高度使其不撞击限位块，即对空气弹簧充气来增大座椅刚度，座椅悬架等效刚度与座椅高度的关系如式(4)所示，经过计算可得到座椅悬架刚度。根据上述经验建立的模糊控制规则如表2。

表2 模糊控制器2模糊规则

使用Simulink搭建模糊控制的半主动座椅单自由度仿真模型，仿真时间为10 s，仿真步长为0.001 s，“人—椅”质量为80 kg，仿真结果如图10和图11。

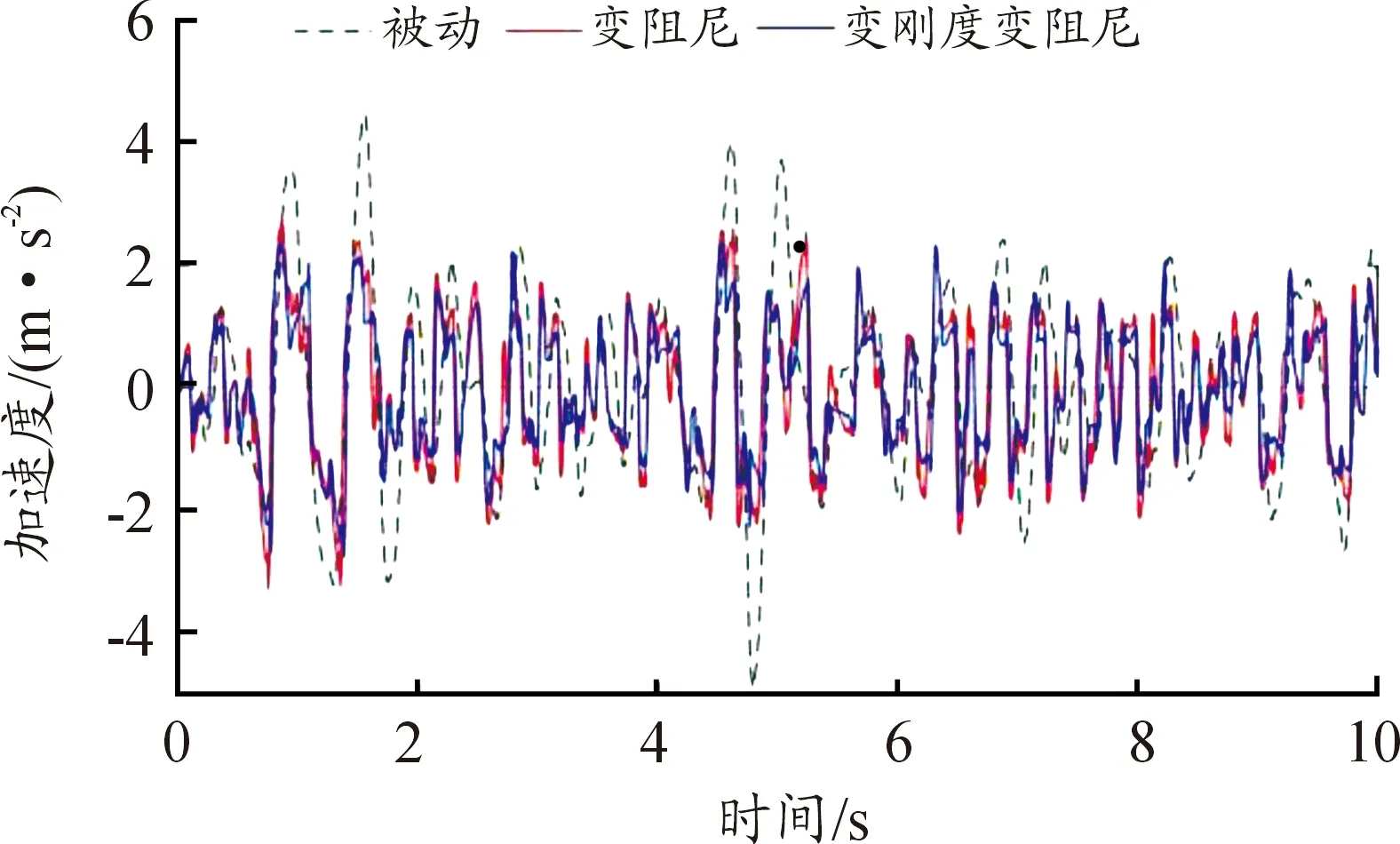
图10 座椅悬架加速度响应曲线

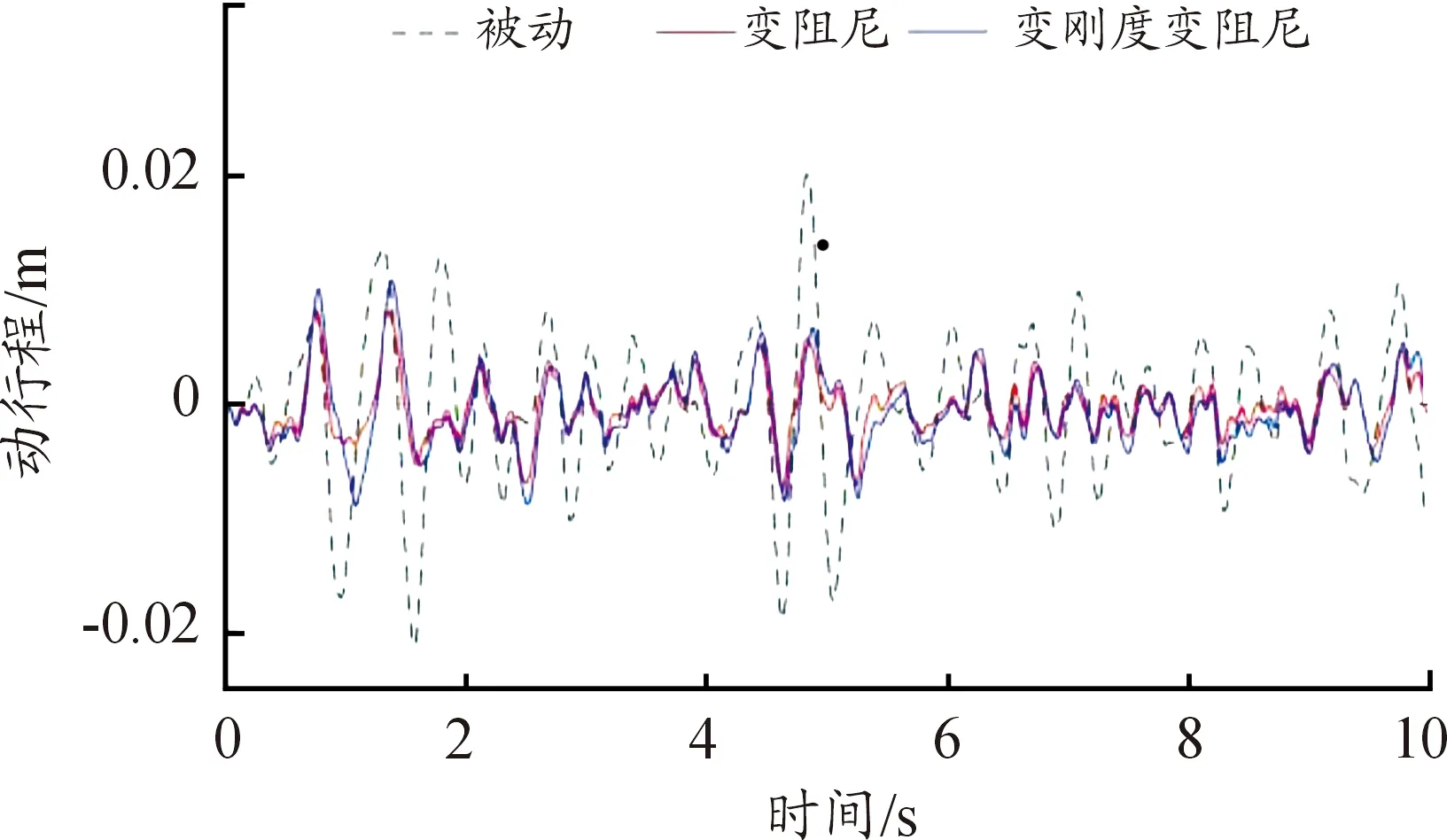
图11 座椅悬架动行程响应曲线

图10所示为座椅悬架模糊控制下加速度响应曲线，被动座椅悬架加速度均方根为1.739 0 m/s2，模糊控制策略下变阻尼座椅悬架加速度均方根为1.177 9 m/s2，加速度均方根减少了32.27%，模糊控制策略下变刚度变阻尼座椅悬架加速度均方根为1.025 8 m/s2，加速度均方根减少了41.01%，从图11可知模糊控制策略下变刚度变阻尼座椅悬架动行程相比被动座椅悬架明显减小，该变刚度变阻尼座椅悬架比被动座椅和单独变阻尼控制的座椅拥有更好的减振性能。

4 试验

4.1 试验平台整体方案

为了验证半主动座椅悬架的减振性能和模糊控制策略的控制效果，设计了如图12所示的半主动座椅控制系统，基于此系统搭建了如图13所示的磁流变座椅振动控制试验平台。

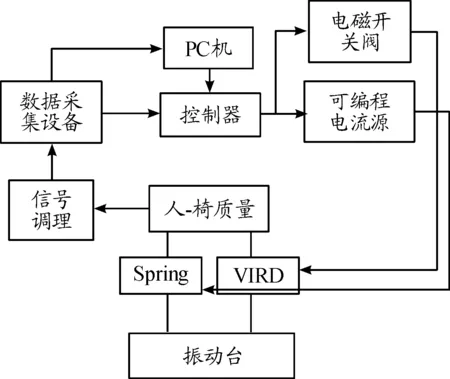
图12 磁流变座椅悬架控制系统框图

图13 磁流变座椅悬架控制系统试验台

在振动试验控制仪的ShakerController控制软件里设定好所需激励信号，该系统会控制一自由度振动台产生相应的振动激励。在座椅悬架上下底板处各安装有一个8711-01-005型量程5g的加速度传感器，上底板传感器灵敏度为927.32 mv/g，下底板传感器灵敏度为928.46 mv/g。在磁流变阻尼器处安装有一个位移传感器，通过数据采集设备采集座椅的振动响应信号，信号经过计算机进行处理，在speedgoat仿真平台下获得磁流变阻尼器的控制电流，并向电流源输送电流控制信号，同时获得空气弹簧的充放气信号，并控制开关电磁阀充放气。此时通过数据采集设备反馈回的座椅上底板加速度响应和磁流变阻尼器处位移传感器信号来时刻修正电流控制信号和电磁阀充放气信号。

4.2 试验结果与分析

因为该振动台无法产生随机激励信号，这里通过正弦激励来验证半主动座椅减振效果，座椅悬架固有频率在 2 Hz 左右。

当座椅悬架共振时，被动座椅悬架与模糊控制下的座椅悬架加速度响应如图14所示，被动座椅悬架加速度均方根为3.572 3 m/s2，仅对磁流变阻尼器进行控制时座椅上底板加速度均方根值为2.185 7 m/s2，加速度均方根值减少了38.81%，对空气弹簧和磁流变阻尼器进行联合控制时座椅上底板加速度均方根值为1.945 7 m/s2，加速度均方根值减少了45.53%，该变刚度变阻尼座椅悬架比被动座椅悬架和变阻尼座椅悬架拥有更好的隔振性能。

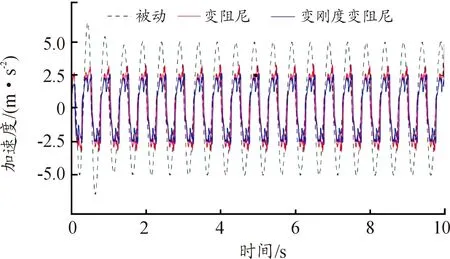
图14 2 Hz 16 mm正弦激励下加速度响应曲线

5 结论

本文制定了基于空气弹簧和磁流变阻尼器的半主动座椅模糊控制策略，并进行验证。通过仿真和试验结果表明，该控制方法实现了座椅悬架的刚度和阻尼调节，相比被动座椅和单独变阻尼控制的座椅，该半主动座椅拥有更好的减振性能。