集值优化问题近似解的最优条件
吴 蕾,孟旭东
(南昌航空大学 科技学院,江西 共青城 332020)
集值优化问题最优条件与对偶性的研究成果既可以丰富和发展集值优化问题的理论与算法,为向量优化在交通均衡、资源分配、工程管理、工程技术等领域的应用提供重要的理论依据,又能快速促进向量优化及其相关问题的理论与算法的发展,对学科发展有重要意义.
凸性在研究集值优化问题的最优条件和对偶性方面扮演着重要角色.近年来,学者们借助凸性在向量优化问题研究中取得丰富研究成果.Yang等提出广义锥-次类凸和近似锥-次类凸的概念,给出它们的关系.Sach提出一种新的内部锥-类凸性,建立择一性定理,得到有效解、弱有效解和Benson真有效解的Kuhn-Tucker型和Lagrange型最优条件.Xu等在近似锥-次类凸条件下分析超有效解的Lagrange型最优条件和强有效解的Kuhn-Tucker型最性条件.Hanson引入新的广义不变凸性的概念,研究一类非线性规化问题解的性态.文献[8-10]在一种新的不变凸性条件下,分析集值优化问题解集的最性条件和稳定性.
另一方面,学者们对对偶问题的研究也取得丰硕的阶段性成果.文献[11-13]讨论多种类型集值优化问题的对偶性.文献[14-15]提出集值映射的相依上图导数的概念,研究集值优化问题稳定性.文献[16]推广文献[14-15]中的相依上图导数概念,给出锥-逼近多值函数的概念,并在不变凸性假设下,刻画集值优化问题的弱有效解极小元.在广义不变凸性假设下,文献[17]得到集值优化问题弱近似解的对偶定理和最优条件.
论文在文献[3,10,16-17]的研究成果基础上,在实赋范线性空间中给出一类集值优化问题的最优条件和对偶定理.
1 准备工作
设X
,Y
,Z
为实赋范线性空间,X
,Y
,Z
分别为X
,Y
,Z
的拓扑对偶空间,C
⊆Y
,D
⊆Z
为点凸锥.记C
,D
分别为C
,D
的拓扑对偶锥,C
为C
的拟内部,cone(M
)为Y
中非空子集M
的锥包,分别定义为


M
):={λm
:m
∈M
,λ
≥0}.设B
为凸锥C
的非空凸子集,称B
为C
的一个基当且仅当0∈cl(B
)和C
=cone(B
).记C
(B
):={f
∈C
:对任何的b
∈B
,存在t
>0,使得f
(b
)≥t
},易知C
(B
)≠∅,C
(B
)⊆C
,以及对每个η
∈(0,δ
),δ
:=inf{||b
||:b
∈B
}>0.记C
的点凸锥为C
(B
):=cone(B
+ηU
),其中U
为X
中的单位球.设G
:X
→2为集值映射,G
的定义域、图和上图分别为dom(G
):={x
∈X
:G
(x
)≠∅},graph(G
):={(x
,y
)∈X
×Y
:y
∈G
(x
)},epi(G
):={(x
,y
)∈X
×Y
:y
∈G
(x
)+C
}.
定义1
设G
:X
→2为给定集值映射,点(x
,y
)∈graph(G
)给定,DG
(x
,y
):X
→Y
为一个映射,若满足epi(DG
(x
,y
))=T
(epi(G
),(x
,y
)),则称映射DG
(x
,y
)为G
在点(x
,y
)处的相依上图导数.定义2
设G
:X
→2为给定集值映射,点(x
,y
)∈graph(G
)给定,A
,(,):X
→2为一个集值映射,若满足:(1)epi(A
,(,))为闭锥;(2)epi(A
,(,))⊆T
(epi(G
),(x
,y
)).则称映射A
,(,)为G
在点(x
,y
)处的C
-逼近多值函数.注1
(1)由文献[16]知,集值映射相依上图导数是集值映射锥-逼近多值函数的特例.(2)由文献[16]中例7知,集值映射锥-逼近多值函数存在,但其相依上图导数不存在.
定义3
设G
:X
→2为给定集值映射,点(x
,y
)∈graph(G
)给定,ξ
(x
,y
):X
→X
是一个函数,且A
:X
→2为一个集值映射,若满足
G
在点(x
,y
)处关于ξ
(x
,y
)为A
-不变凸的.定义4
设ε
≥0,点e
∈C
给定,G
:X
→2为给定集值映射,点(x
,y
)∈graph(G
)给定,ξ
(x
,y
):X
→X
是一个函数,且A
:X
→2为一个集值映射,若满足
G
在点(x
,y
)处关于ε
·e
与ξ
(x
,y
)为A
-次不变凸的.注2
若G
在点(x
,y
)处关于ξ
(x
,y
)为A
-不变凸的,则G
在点(x
,y
)处关于ε
·e
与ξ
(x
,y
)为A
-次不变凸的.反之不然,见文献[17]中例1.2 最优充分条件
设F
:X
→2,G
:X
→2为集值映射,且dom(F
)=dom(G
)=X.
讨论集值优化问题(简记问题(SOP)).
x
,y
)∈graph(F
),z
∈G
(x
)∩(-D
),F
和G
分别在点(x
,y
)和(x
,z
)处存在C
-逼近多值函数A
,(,)和D
-逼近多值函数A
,(,),且dom(A
,(,))=dom(A
,(,))=X.
假若点x
∈X
,y
∈F
(x
)且G
(x
)∩(-D
)≠∅,则称点(x
,y
)∈X
×Y
为问题(SOP)的可行点,记问题(SOP)可行点的全体为Σ.
定义5
(1)设ε
≥0,点e
∈B
给定,若存在η
∈(0,δ
)及点y
∈F
(x
),使得(F
(Σ
)+ε
·e
-y
)∩(-intC
(B
))=∅,则称点x
∈Σ
为问题(SOP)的Henig近似解,此时,称点(x
,y
)∈graph(F
)为问题(SOP)的Henig近似解极小点.(2)设ε
≥0,点e
∈C
{0}给定,若存在点凸锥H
⊆Y
,满足C
{0}⊆intH
及点y
∈F
(x
),使得(F
(Σ
)+ε
·e
-y
)∩((-H
){0})=∅,则称点x
∈Σ
为问题(SOP)的Global近似解,此时,称点(x
,y
)∈graph(F
)为问题(SOP)的Global近似解极小点.定理1
设ε
≥0,点e
∈B
给定,点(x
,y
)∈graph(F
)为问题(SOP)的可行点,点z
∈G
(x
)∩(-D
),假设满足以下条件:(1)F
在点(x
,y
)处关于ε
·e
与ξ
(x
,y
,z
)是A
-次不变凸的;(2)G
在点(x
,z
)处关于ξ
(x
,y
,z
)是A
-不变凸的;(3)存在(f
,g
)∈C
(B
)×D
,使得
(1)
且
g
(z
)=0.(2)
则点(x
,y
)为问题(SOP)的Henig近似解极小点.证明
假设点(x
,y
)不是问题(SOP)的Henig近似解极小点,则(F
(Σ
)+ε
·e
-y
)∩(-intC
(B
))≠∅,所以存在点x
∈Σ
及点y
∈F
(x
),使得y
+ε
·e
-y
∈-intC
(B
).注意到f
∈C
(B
),有f
(y
+ε
·e
-y
)<0,再结合条件(1),得
F
(x
)+ε
·e
-y
⊆A
,(,)(ξ
(x
,y
,z
)(x
))+C
,故
y
+ε
·e
-y
∈A
,(,)(ξ
(x
,y
,z
)(x
))+C
,所以,有
f
(A
,(,)(ξ
(x
,y
,z
)(x
)))≤f
(y
+ε
·e
-y
)<0,f
(A
,(,)(ξ
(x
,y
,z
)(x
)))<0.(3)
另外,由条件(2),知
G
(x
)-z
⊆A
,(,)(ξ
(x
,y
,z
)(x
))+D.
由x
∈Σ
知,存在z
∈G
(x
)∩(-D
),使得z
-z
∈A
,(,)(ξ
(x
,y
,z
)(x
))+D
,再由g
∈D
,得g
(A
,(,)(ξ
(x
,y
,z
)(x
)))≤g
(z
-z
),结合g
(z
)≤0与g
(z
)=0,知g
(z
-z
)≤0,且g
(A
,(,)(ξ
(x
,y
,z
)(x
)))≤0.(4)
由式(3),(4),得
f
(A
,(,)(ξ
(x
,y
,z
)(x
)))+g
(A
,(,)(ξ
(x
,y
,z
)(x
)))<0,这与式(1)矛盾,故点(x
,y
)为问题(SOP)的Henig近似解极小点.类似可得问题(SOP)的Global近似解极小点的最优充分定理,即定理2.
定理2
设ε
≥0,点e
∈C
{0}给定,点(x
,y
)∈graph(F
)为问题(SOP)的可行点,点z
∈G
(x
)∩(-D
),且假设满足以下条件:(1)F
在点(x
,y
)处关于ε
·e
和ξ
(x
,y
,z
)是A
-次不变凸的;(2)G
在点(x
,z
)处关于ξ
(x
,y
,z
)是A
-不变凸的;(3)存在(f
,g
)∈C
×D
,使得式(1),(2)同时成立.则点(x
,y
)为问题(SOP)的Global近似解极小点.3 对偶性
3.1 Mond-Weir型对偶
讨论问题(SOP)的Mond-Weir型对偶问题(MWD-I)与(MWD-II).



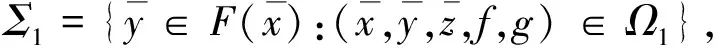

定义6
(1)设ε
≥0,点e
∈B
给定,若存在η
∈(0,δ
),使得

ε
≥0,点e
∈C
{0}给定,若存在点凸锥H
⊆Y
,满足C
{0}⊆intH
,使得


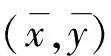
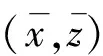
则

(5)


(6)
由点(x
,y
)为问题(SOP)的可行点,有G
(x
)∩(-D
)≠∅,故存在点z
∈G
(x
)∩(-D
),使得g
(z
)≤0.

(7)
由式(6),(7),得
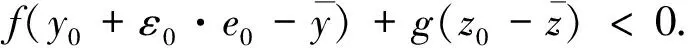
(8)
注意到条件(1),(2),知

且

因此,有

(9)
且

(10)
结合式(8)~(10),得

这与(MWD-I)的限制条件矛盾,故式(5)成立.
定理4
(强对偶) 设ε
≥0,点e
∈B
给定,点(x
,y
)为问题(SOP)的Henig近似解极小点,存在(f
,g
)∈C
(B
)×D
及点z
∈G
(x
)∩(-D
),使得式(1),(2)成立,则点(x
,y
,z
,f
,g
)为问题(MWD-I)的可行点.此外,若问题(MWD-I)的弱对偶定理3成立,则点(x
,y
,z
,f
,g
)为问题(MWD-I)的Henig近似解极大点.

x
,y
,z
,f
,g
)为问题(MWD-I)的Henig近似解极大点.
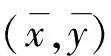

x
∈Σ
,y
∈F
(x
),使得
f
∈C
(B
),知
(11)

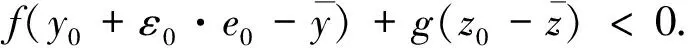
(12)
另一方面,由定理3中的条件(1),(2),知

且

结合式(12),知

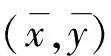
类似可得问题(MWD-II)的弱对偶、强对偶和逆对偶定理.

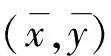
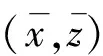

定理7
(强对偶) 设ε
≥0,点e
∈C
{0}给定,点(x
,y
)为问题(SOP)的Henig近似解极小点,且存在(f
,g
)∈C
×D
及点z
∈G
(x
)∩(-D
),使得式(1),(2)成立,则点(x
,y
,z
,f
,g
)为问题(MWD-II)的可行点.此外,若问题(MWD-II)的弱对偶定理6成立,则点(x
,y
,z
,f
,g
)为问题(MWD-II)的Henig近似解极大点.
3.2 Wolfe-型对偶
设点c
∈B
给定,讨论问题(SOP)的Wolfe-型对偶问题,记为(WD-I).
c
∈C
{0}给定,讨论问题(SOP)的Wolfe-型对偶问题,记为(WD-II).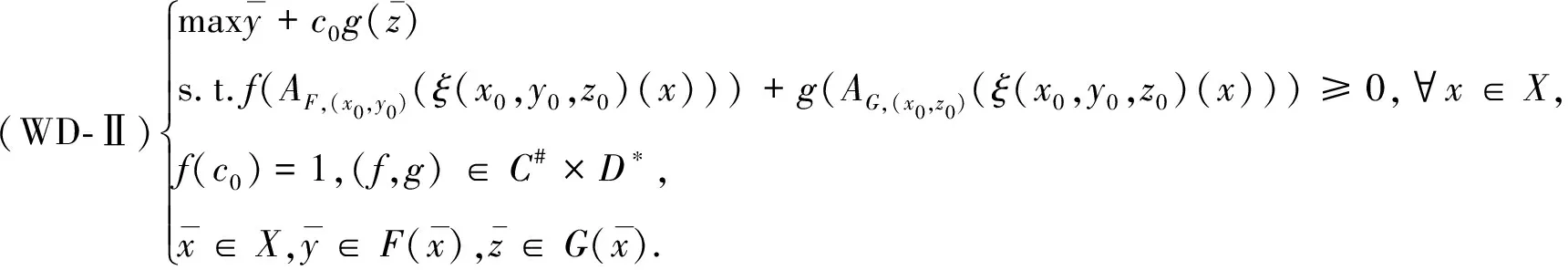



定义7
(1)设ε
≥0,点e
∈B
给定,若存在η
∈(0,δ
),使得

ε
≥0,点e
∈C
{0}给定,若存在点凸锥H
⊆Y
,满足C
{0}⊆intH
,使得


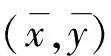
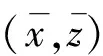
则
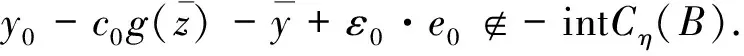
(13)
证明
假设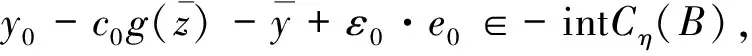
G
(x
)∩(-D
)≠∅,取点z
∈G
(x
)∩(-D
),则g
(z
)≤0,故c
g
(z
)∈(-C
),且
f
∈C
(B
),f
(c
)=1,有
类似定理3的论证过程,得

这与问题(WD-I)的条件矛盾,故式(13)成立.
定理10
(强对偶) 设ε
≥0,点e
∈B
给定,点(x
,y
)∈graph(F
)和z
∈G
(x
)∩(-D
),点(x
,y
)是问题(SOP)的Henig近似解极小点,存在(f
,g
)∈C
(B
)×D
,满足f
(c
)=1,使得式(1),(2)成立,则点(x
,y
,z
,f
,g
)为问题(WD-I)的可行点.此外,若问题(WD-I)的弱对偶定理9成立,则点(x
,y
,z
,f
,g
)为(WD-I)的Henig近似解极大点.证明
由式(1),(2)成立,易知点(x
,y
,z
,f
,g
)为(WD-I)的可行点.现证(W
-ε
·e
-(y
+c
g
(z
)))∩(-intC
(B
))=∅.(14)
设点(x
,y
,z
,f
,g
)为问题(WD-I)的可行点,满足y
+c
g
(z
)∈W
,且y
+c
g
(z
)-y
-c
g
(z
)-ε
·e
∈intC
(B
).由g
(z
)=0,知y
+c
g
(z
)-y
-ε
·e
∈intC
(B
),这与式(13)矛盾,式(14)成立,故点(x
,y
,z
,f
,g
)为(WD-I)的Henig近似解极大点.
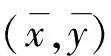



f
∈C
(B
),有
(15)


类似定理3的论证过程,对问题(WD-I),有

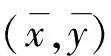
类似可得问题(SOP)的Wolfe-型对偶问题(WD-II)的弱对偶、强对偶和逆对偶定理.

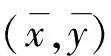
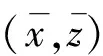
则

定理13
(强对偶) 设ε
≥0,点e
∈C
{0}给定,点(x
,y
)为问题(SOP)的Global近似解极小点,存在(f
,g
)∈C
×D
,满足f
(c
)=1,对于点z
∈G
(x
)∩(-D
),式(1),(2)成立,则点(x
,y
,z
,f
,g
)为问题(WD-II)的可行点.此外,若问题(WD-II)的弱对偶定理12成立,则点(x
,y
,z
,f
,g
)为问题(WD-II)的Global近似解极大点.
4 结束语
论文在文献[3,10,16-17]研究成果基础上研究一类集值优化问题近似解的最优条件和对偶性.在赋范线性空间中,借助锥-次不变凸性的基本假设,结合分析的方法,证明了集值优化问题的Henig近似解极小点和Global近似解极小点的最优充分定理,并建立了两种近似解的Mond-Weir型和Wolfe型对偶定理.
