一类重尾极值指数估计

张绿云，陈守全

西南大学 数学与统计学院，重庆 400715

其中

证明了其弱相合性和渐近正态性，并在均方误差最小的情况下，给出了中调节参数k的最优选择．

设{Xn，n≥1}是一列独立同分布的随机变量序列，其共同的分布函数为F(x)，X1，n≤…≤Xn，n为X1，…，Xn的顺序统计量．若对非退化分布函数G(x)，存在规范化常数an>0，bn∈R，对一切G(x)的连续点有

成立，则称F属于G的吸引场，记为F∈D(G)．文献[1-2]证明G(x)的形式必为

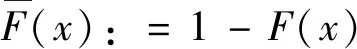
(1)

则称分布函数F是重尾分布函数．

对于极值指数的研究，前人已经得到较好的结论．当γ>0时，文献[3]提出了著名的的Hill估计量．而作为Hill估计的一个推广，文献[9]提出了如下定义的调和矩估计

其中1≤k≤n-1且β>0是调谐参数．

本文受文献[9]中估计量的启发，提出定义如下的一类关于重尾极值指数的新估计

(2)

其中β1≠β2是调谐参数β的两个取值，且

(3)

1 主要结果

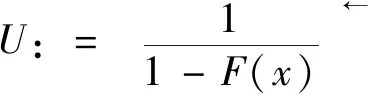
F∈D(G)当且仅当

(4)

对所有x>0和某些正可测函数a(t)成立．注意，如果γ=0，则(4)式的右边为lnx．

为简化定理的表示，本文规定以下记号：

(5)

下面给出本文的主要结果．

此外，若二阶条件(3)成立，且存在λ∈R使得

其中

Vβ1，β2(γ)如(5)定义．

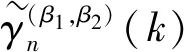
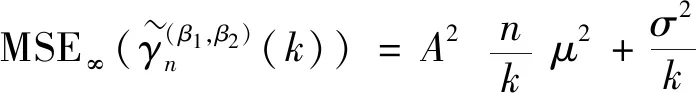
则

此外，

其中s←是s∈RV2ρ-1的广义逆函数，且

2) 假设A(t)=Ctρ，则1)中的k0为

单层干燥（6 h）、双层干燥（6 h）、三层干燥（8 h） 的最终样品水分含量分别9.33%，7.77%和8.68%，双层物料最终湿基含水量最低且各层物料最终湿基含水量无显著差异（p＞0.05），物料均匀性最好。

其中└x┘表示不超过x的最大整数．此外，

且

2 定理的证明

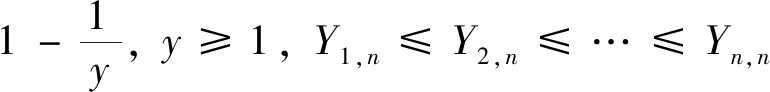
下面对本文的主要结果进行证明．

定理1的证明由二阶条件可得

因此

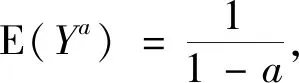
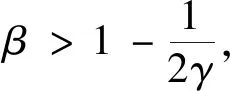
那么

从而

现定义

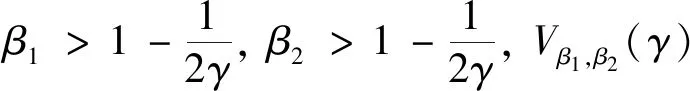
因此

其中

设

由于

故现在利用映射g(θ)来构造一个关于γ的估计量．应用Delta方法，可得

其中μ，σ2如前定义．

定理2的证明类似文献[10]中的定理可得结果．