基于BDS三频相位多路径误差的土壤湿度反演

聂士海 张显云 付 婷 赵飞飞

1 贵州大学矿业学院，贵阳市花溪区，550025

自Larson等[1]首次提出采用GPS信噪比(signal-to-noise ratio，SNR)反演土壤湿度以来，SNR一直被当作GNSS-IR的主要数据源。但SNR对大多数GNSS用户无用，导致SNR并不总存在于GNSS的原始文件中[2]；且以SNR时间序列作为系统输入的GNSS-IR的性能在很大程度上取决于SNR的观测质量和SNR直接分量(趋势项)的成功去除[3]，而实际SNR难免会受到异常噪声的影响，从而导致采用低阶多项式去趋势项后获得的表征多路径信息的SNR反射分量可能“不纯”。受制于上述2个原因，基于SNR时间序列的GNSS-IR可能无法得以实施或其性能可能受到严重影响。为此，Ozeki等[2]提出一种基于L4观测值的GNSS-IR雪深探测方法——L4方法。虽然L4观测值独立于几何距离，但由于受频间电离层延迟误差的影响，其反演精度不及SNR。

GNSS各系统大都发射有三频载波信号，据此可构建出无几何无电离层延迟的多路径模型，从而获得“高质量”的多路径误差。研究表明，基于三频多路径误差和SNR的雪深反演精度相当[3]。但土壤与积雪具有不同的反射特性，且土壤湿度和雪深反演在方法上存在差异，而基于多路径误差的土壤湿度反演尚未见报道。为丰富GNSS-IR土壤湿度反演的数据源，提升GNSS服务于环境监测的能力，本文提出一种基于BDS三频载波相位多路径误差的GNSS-IR土壤湿度反演方法，并利用现场实测的土壤湿度数据对其可行性和性能进行评价。

1 基于三频多路径误差的GNSS-IR土壤湿度反演

多路径误差原理及计算见文献[3-5]，本文不再赘述。多路径误差可近似表示为：

(1)

式中，β(t)为多路径误差，Ad和Am分别为直接信号和反射信号的振幅，其中Am=κAd，κ为幅度衰减因子，是反射系数和天线增益的函数，δφ为相位延迟。

为获得表征土壤湿度变化趋势的参量,以多路径误差为系统输入(观测值),幅度衰减因子和延迟相位为待估参数，对式(1)进行线性化，可得误差方程，进而采用最小二乘平差即可解求出对应时段的幅度衰减因子和延迟相位。其中，延迟相位初值可由式(2)确定：

(2)

式中，ΔS为反射信号较直接信号多经过的路径长度，λ为载波波长，t为观测历元，H为接收机天线高，α为卫星高度角。确定延迟相位初值时，α取值为第1个土壤湿度样本采集时刻对应的卫星高度角。为简化问题，忽略天线增益的影响，幅度衰减因子初值取为反射系数经验值0.3[3]。

考虑到天线高和卫星高度正弦值变化较小，而本文关注的重点是延迟相位本身的变化趋势，故在数据处理时所有时段均采用相同的延迟相位初值。数据处理遵循以下原则：

1)对载波相位观测值进行周跳探测与修复；

2)假设幅度衰减因子和延迟相位短时间内无变化；

3)为避免延迟相位和土壤湿度采集时间过于悬殊，考虑到必要观测数，以土壤湿度采集时刻为参考，取前后各5个历元的多路径误差作为观测值，即忽略短期内延迟相位随卫星高度角的变化，将每个时段选定的多路径误差看为对同一参量的重复观测，继而采用最小二乘平差方法，在每个时段分别求解出一个表征土壤湿度变化趋势的延迟相位。

基于三频多路径误差的GNSS-IR土壤湿度反演算法流程如图1所示。

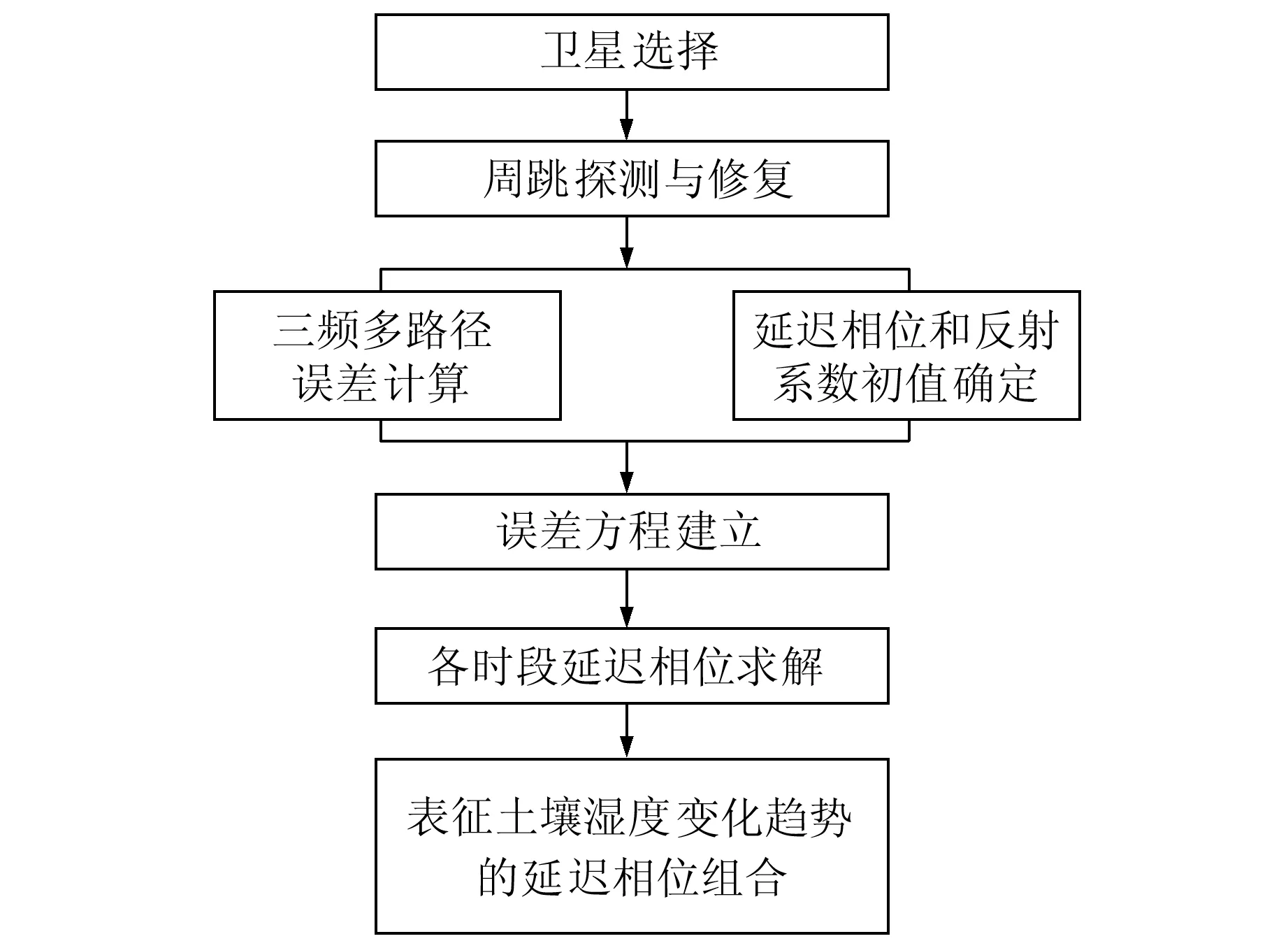
图1 算法流程Fig.1 The algorithm flow chart

2 实验数据

2.1 载波相位观测值采集

载波相位观测值采集于贵州大学西区校园内(26.45°N，106.66°E)。实验地点南侧平整性较好，北侧地形起伏较大，总体呈南低北高的狭长带状走势；东西方向约 60 m、南北方向约320 m范围内除分布有零星杂草外，无明显遮挡物和其他多路径反射源，此范围外为公路和建筑物。

载波相位观测值采集时间为 2019-07-18～26，每天采集时长不短于4 h。GNSS 接收机及参数设置见表1。

2.2 土壤湿度测量

同步于载波相位观测值，土壤湿度采样间隔为1 h，取样深度约4 cm。土壤湿度测量采用的传感器为顺科达TR-8D土壤水分测定仪，其测量精度为±2%，测量范围为0～100%。鉴于GNSS卫星反射信号主要来自第一菲涅尔反射区，为确定土壤湿度样本的采集位置，绘制实验站点的第一菲涅尔反射区(图2)。

表1 接收机及参数设置

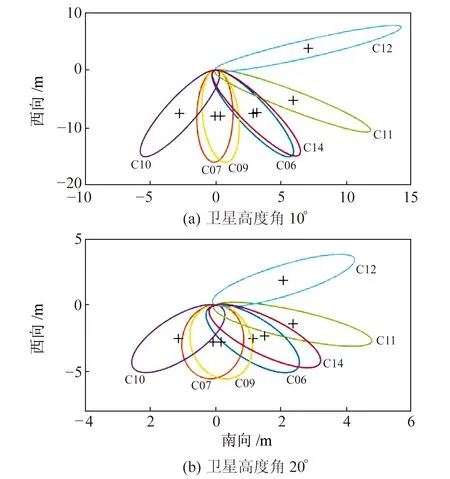
图2 实验站点第一菲涅尔反射区Fig.2 The first Fresnel reflection area of the test site

图2(a)、2(b)分别为卫星高度角10°和20°时的第一菲涅尔反射区。由图可见，椭圆中心与接收机间的距离随卫星高度角的升高而减小，且不同历元卫星的方位也有所不同。因此，考虑到卫星信号反射足迹的变化，为削弱不同位置土壤湿度差异性的影响，实际量测时以GNSS接收机为中心，结合第一菲涅尔反射区，分别进行不同距离(5 m、10 m、15 m)和不同方位的土壤湿度采集，每个时段测得土壤湿度样本共15个，最后取各时段平均值作为对应时段的土壤湿度，即

(3)

由于未架设永久性的监测站，同时受降雨天气等因素的影响，人工采集土壤湿度难度大，故得到的土壤湿度在时间上并不连续。根据研究区BDS低卫星高度角三频载波相位信号的覆盖情况，结合土壤湿度测量时间，本实验共筛选出32对观测值。

3 实验分析

以土壤湿度采集时间为参考，结合卫星高度角、方位角及信号载波数，确定各时间节点具有三频载波信号的BDS卫星。结合上述原理及方法，通过平差求得对应土壤湿度采集时刻的延迟相位，并绘制土壤湿度及延迟相位的时间变化趋势图(图3)。

图3 土壤湿度与延迟相位相关性Fig.3 Correlation between soil moisture and delay phase

由图3可知，延迟相位和土壤湿度均存在多个明显的峰值，总体变化趋势具有较强一致性，两者相关系数达到0.97，为显著相关。为进一步描述土壤湿度与延迟相位的关系，以延迟相位为自变量(x)、土壤湿度为因变量(y)进行一元线性回归建模(图4)，土壤湿度回归残差见图5。

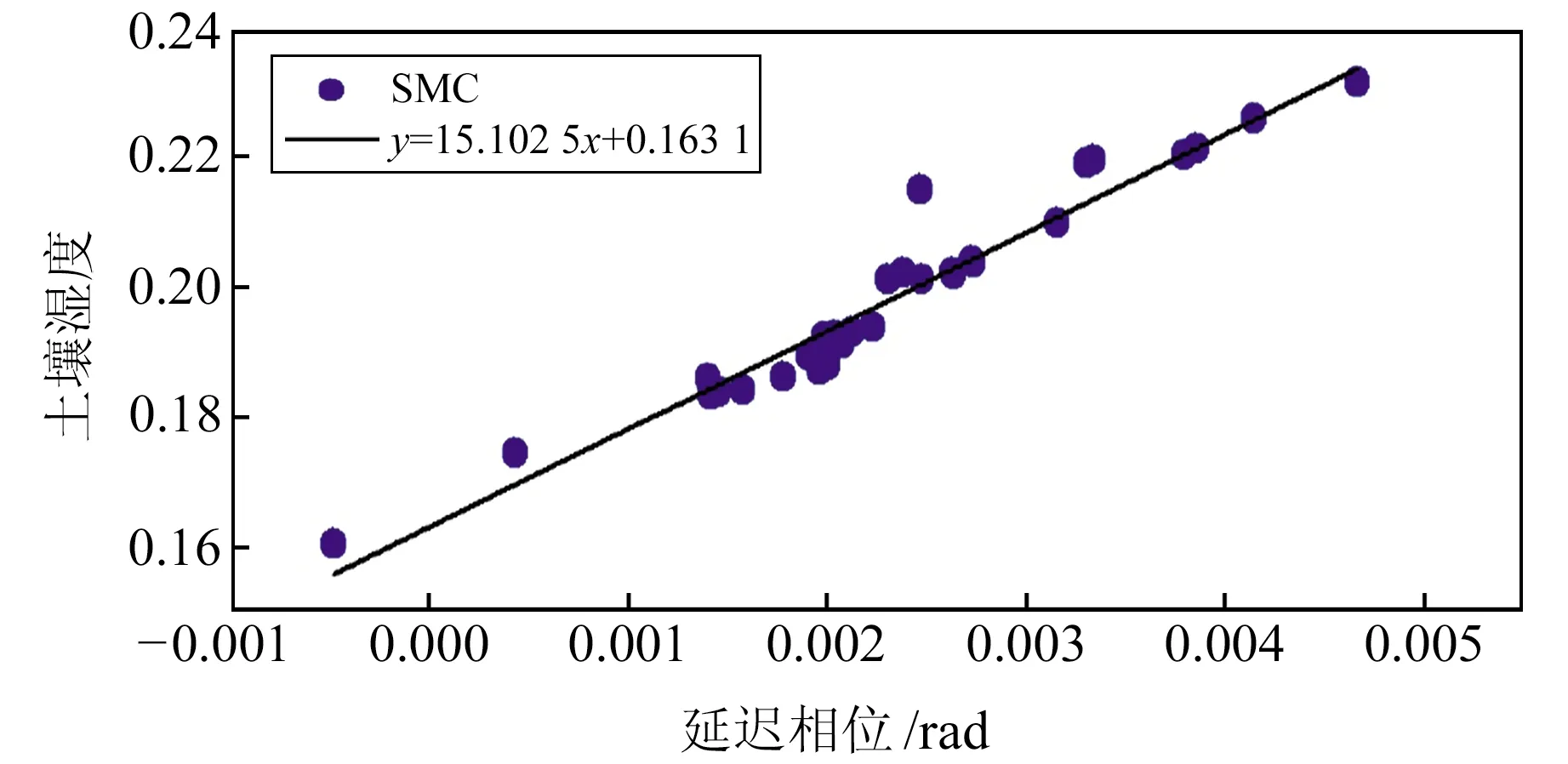
图4 土壤湿度与延迟相位线性关系Fig.4 Linear relationship between soil moisture and delay phase

图5 土壤湿度回归残差Fig.5 The regression residual of soil moisture

从图4可以看出，土壤湿度在回归直线y=15.102 5x+0.163 1上下波动，且偏离度较小。由图5可知，土壤湿度回归值残差均位于-0.005～0.015之间，引入统计学中F检验，经查表得F0.005(1,30)=9.18，而检验量F=433.38，故回归效果显著。以上结果进一步说明，自变量(延迟相位)与因变量(土壤湿度)间存在较强的线性相关性，说明可利用延迟相位反演出高精度的土壤湿度信息。

4 结 语

本文提出一种基于BDS多路径误差的土壤湿度反演方法。实验结果表明，由相位多路径误差导出的延迟相位与土壤湿度间存在较强的相关性，相关系数高达0.97，与文献[6]中同一地点的基于SNR的土壤湿度反演精度相当，有力证明了该方法的可行性和有效性。此外，相较于基于SNR的土壤湿度反演，由于本文方法无需诊断信号频率，仅需较少历元的多路径误差便可计算出延迟相位，因此更容易实现GNSS-IR土壤湿度反演的高时间分辨率。基于多路径误差的土壤湿度反演丰富了GNSS-IR的数据源，增强了GNSS-IR的可靠性。随着GNSS三频信号的不断扩充，多路径误差将在GNSS环境监测中扮演重要角色。但单卫星系统往往不能保证任意时刻均有低卫星高度角覆盖的三频载波信号，故为提高GNSS-IR土壤湿度估计的时间分辨率，多系统组合GNSS-IR将会成为未来的发展趋势。