基于CEEMDAN的GNSS变形监测去噪方法

汤 俊 李垠健 高 鑫

1 华东交通大学土木建筑学院，南昌市双港东大街808号，330013 2 华东交通大学土木工程国家实验教学示范中心，南昌市双港东大街808号，330013

GNSS变形监测具有测站间无需通视和全天候自动观测等优点[1]，被广泛应用于工程结构的健康监测。由于数据采集过程中易受天气、树木遮挡、多路径效应等多种因素影响，GNSS变形序列中常包含测量噪声，这些噪声会严重影响测量精度，导致监测物的变形信息不准确。因此，有必要对监测数据进行滤波处理。常见的变形监测数据滤波方法有小波去噪[2-3]、Kalman滤波[4]、经验模态分解[5-8](empirical mode decomposition, EMD)等。GNSS变形监测受背景噪声影响具有非平稳、高频率、重复性强等特点，EMD及其改进方法在处理该类信号时具有明显优势。本文针对EMD分解中的噪声传递以及真实信号缺失等问题，提出基于EMD的改进方法——CEEMDAN，在分解过程中加入有限次自适应白噪声，可有效避免模态混叠和信号失真。通过比较CEEMDAN、EMD和小波去噪方法的去噪效果，利用仿真数据与GNSS边坡实测监测数据进行实验分析，验证该方法的有效性和可靠性。

1 CEEMDAN方法构建

1.1 CEEMDAN原理

EMD在构建包络线时使用三次样条法，无法判断信号两端是否为极值点，所以会产生端点效应。在分解过程中，EMD采取递归分解，在频率尺度不连续时，无法正确分离不同尺度的信号，从而造成模态混叠现象。针对该问题，EEMD分解时在序列中间断加入高斯白噪声，由于白噪声具有均值为0的特点，因此在加入数量足够多的情况下白噪声会相互抵消，从而在一定程度上避免模态混叠问题，但分解后的单个IMF仍存在残余噪声，导致残余噪声在高阶IMF和低阶IMF中传递。

CEEMDAN算法是在EEMD基础上发展而来的，针对EEMD分解过程中的噪声传递问题，CEEMDAN在各个分解阶段添加自适应高斯白噪声，得到模态分量后立即进行加总平均计算，同时在后续分解中执行同样操作。该算法可实现在较少的平均次数下，保证重构误差为0，从而有效避免噪声传递的问题。 CEEMDAN方法的具体步骤如下：

1) 在原始信号x(t)中添加I组均值为0的自适应白噪声ωi(t)，第i次信号可表示为：

xi(t)=x(t)+ωi(t)

(1)

式中，i为实验次数1,2,…,I。采用EMD算法对xi(t)进行分解，得到第1个模态分量，然后立即对其进行加总平均计算，得到：

(2)

将原始信号减第1个模态分量得到残余分量：

r1=x(t)-IMF1

(3)

2) 求解第2阶模态分量IMF2，在残余分量r1中继续加入白噪声ωi(t)，构成新的待分解信号：

R1(t)=r1(t)+ωi(t)

(4)

进行i次实验(i=1,2,…,I)，然后对R1(t)进行EMD分解，得到第2个模态分量：

(5)

残余分量可表示为：

r2=x(t)-IMF2

(6)

3) 重复执行步骤1)和2)，直到信号不能再被分解，即信号单调为止，从而得到k个IMF，信号x(t)可表示为：

(7)

1.2 排列熵

排列熵(permutation entropy, PE)[9]、样本熵和模糊熵等概念相同，是衡量时间序列复杂程度的指标，在计算子序列之间复杂程度的同时可引入排列的思想。排列熵具有运算效率高、抗干扰能力强、输出结果简洁等优点，适用于非线性、不规则的信号，对区分IMF频率具有很好的适用性。时间序列越规则，其值越小；时间序列越复杂，即包含噪声越多，其值越大。计算排列熵的基本步骤如下：

1) 设时间长度为N的时间序列X(1),X(2),…,X(n)，重构时间序列，每个子序列以x(i)表示，得到以下序列矩阵：

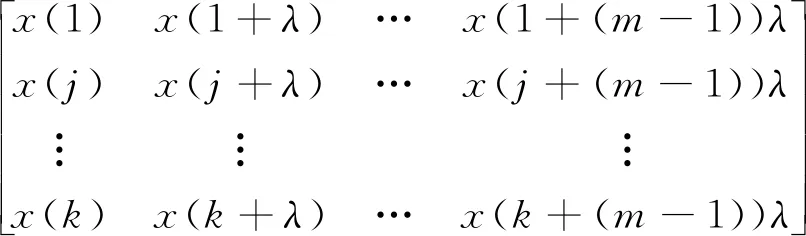
(8)

式中，m为嵌入维数，λ为时间延迟，j=1,2,…,k。

2) 将矩阵中每一行元素组成向量，按升序排列，即

X(i)={x(i+(j1-1)λ)≤x(i+(j2-1)λ)

≤…≤x(i+(jm-1)λ)}

(9)

如果其中有2项相等，则按照ji的下标i进行排序，得到新的符号序列：

S(l)=(j1,j2,…,jm)

(10)

式中，l=1,2,…,k，共产生m!种不同排列，即所有m维子序列X(i)都被映射到m!种不同排列中。

3) 计算所有符号的概率分布，用Pj表示，时间序列的排列熵可表示为：

(11)

HP=H(m)/ln(m!)

(12)

式中，Hp的取值范围为[0,1]。模糊隶属度为模糊集合中研究对象介于0～1之间的某个值，使用模糊隶属度区分高低频分量可得到较为合理的结果。本文基于IMF的特点，经过大量实验，参考文献[10]将PE值的模糊隶属度设定为0.6。当时间序列PE值大于0.6时，可认为是包含噪声的高频信号；PE值小于0.6时，则看作干净信号。计算每一个IMF的PE值，可以筛选出低频信号进行重构。

1.3 CEEMDAN去噪方法

使用CEEMDAN将原始信号分解为不同频率的IMF分量，可避免EMD模态混叠和端点效应问题，分解得到的IMF分量能更清晰地表达自身特征。根据GNSS变形监测序列噪声高频率、周日重复的特点，可认为噪声主要存在于高频分量中，如果直接舍弃则可能丧失其中的真实信息。本文方法对高频分量继续进行小波去噪，使高频分量中的低频信息能得到很好地保留。首先需要找出高频分量与低频分量的分界点K，常用方法有相关系数法、标准化模量累计均值法、平均周期与能量密度乘积法等。本文根据IMF的特性，引入排列熵的概念来区分高频噪声，计算每个IMF的PE值；然后筛选出高频分量，并将其看作噪声信号，将低频分量看作干净信号；对高频分量继续采用小波分析的方法进行去噪，同时对去噪后的高频分量与干净信号进行重构，得到去噪后的信号。具体步骤见图1。

图1 CEEMDAN方法流程Fig.1 Flow diagram of CEEMDAN method

2 仿真实验

为验证本文方法的有效性，构造模拟变形信号对本文方法进行实验。模拟信号由3个正弦函数叠加组成，在该信号的基础上加入高斯白噪声，其函数为：

yt=4sin(2πt/1 000)·sin(2πt/400)+

2sin(2πt/600)+sin(2πt/300)+noise

(13)

式中，noise是信噪比为2 dB的高斯白噪声，采样数为3 000，采样间隔1 s，仿真信号及加噪后信号如图2所示。

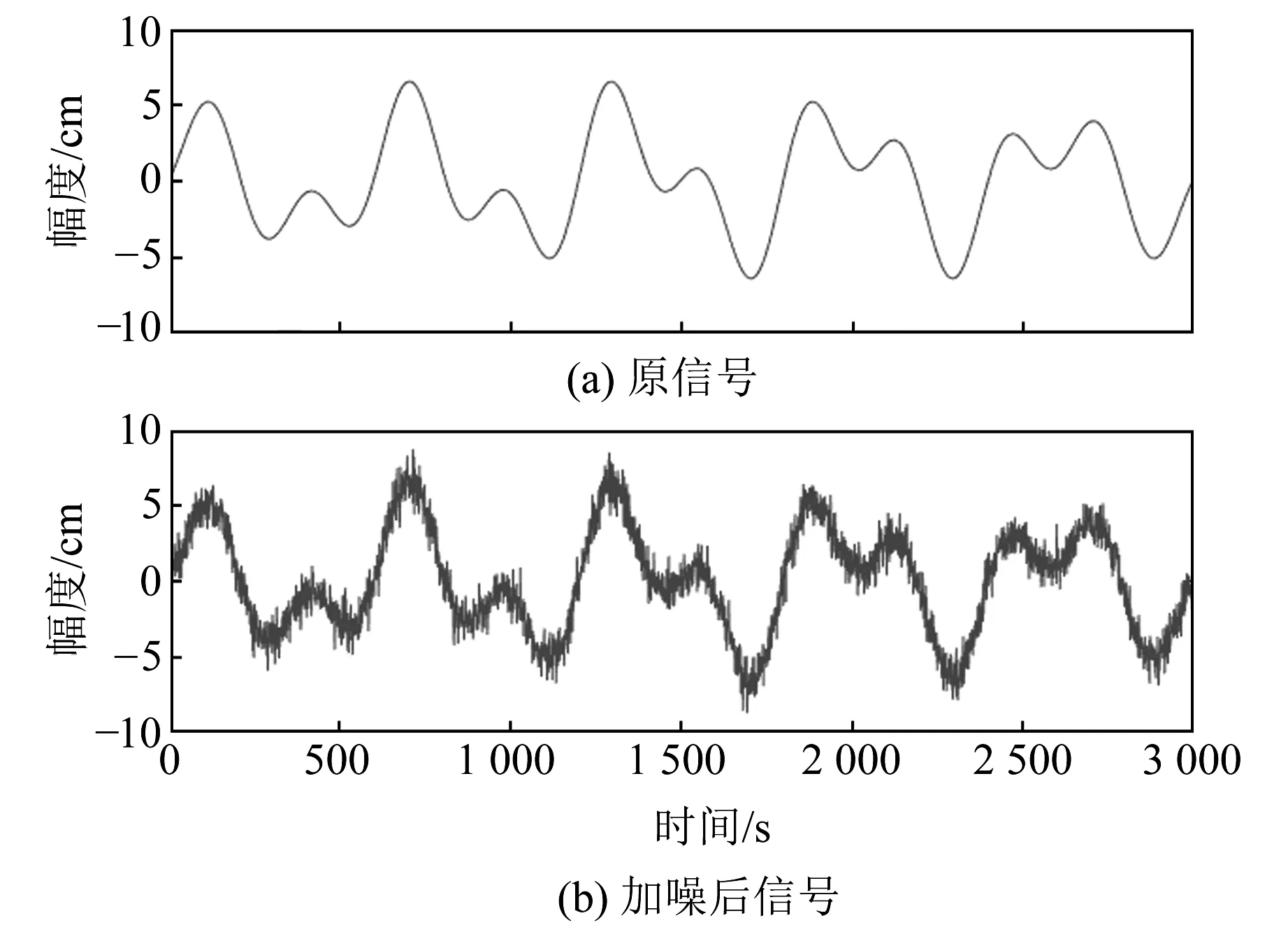
图2 仿真信号序列Fig.2 Simulation signal sequence diagram

采用CEEMDAN算法对加噪后信号进行分解，得到11个IMF分量和1个残余项，各IMF分量如图3所示。从图中可以看出，随着分解次数的增加，信号越来越平滑，表明高斯白噪声主要分布在高频分量上。

图3 基于CEEMDAN方法的分解图Fig.3 Decomposition diagram based on CEEMDAN method

利用排列熵理论确定高频噪声，计算各IMF分量的PE值，结果见表1。由表1可知，前3个IMF分量的PE值大于0.6，可将其看作高频噪声，使用小波变换进行去噪处理。经过多次实验，小波基选择去噪效果较好的db7小波，分解层数为3，选取Heursure(启发式阈值)进行软阈值处理。将去噪后的分量与第4～11个低频分量和残余项进行重构，得到去噪后信号。

表1 各IMF分量排列熵

为验证CEEMDAN方法的去噪效果，对原始信号分别采用小波去噪、EMD、CEEMDAN方法进行去噪，利用信噪比、均方根误差和相关系数3个指标评价去噪效果：

(14)

(15)

(16)

式中，SNR为信噪比，RMSE为均方根误差，R为相关系数，s(i)为原始信号，s′(i)为去噪后信号，L为信号长度。具体去噪效果见表2，从表中可以看出，小波去噪和EMD方法均能起到一定的去噪效果。与之相比，CEEMDAN方法去噪后的信噪比、相关系数均有所提升，均方误差有所降低，表明本文方法具有有效性。

表2 仿真数据去噪效果对比

3 实测数据分析

为进一步验证该方法的可靠性，利用某边坡GNSS变形监测数据进行实验分析。该边坡布设0001、0007、J001、J002共4个监测点，采样频率为1 Hz。实验利用09-01～11-30共91 d的监测数据，选取间隔1 h，截取2 000个历元进行去噪处理。由于篇幅所限，仅展示0001监测点的去噪结果，原始序列和去噪后序列如图4所示，表3为0001监测点N、E、U方向3种去噪方法的效果对比。

图4 实测数据去噪效果Fig.4 Denoising effect of measured data

表3 实测数据降噪效果对比

从图4和表3可以看出，原始监测序列局部呈不平稳态势，具有很大随机性，说明其受到很大的噪声污染。通过分析3个方向的信噪比和相关系数可知，新方法与小波去噪方法相比，信噪比分别提高7.41%、3.15%和6.22%，相关系数分别提高19.6%、27.34%和23.13%；与EMD方法相比，信噪比分别提高6.86%、2.31%和5.97%，相关系数分别提高16.67%、15.64%和21.22%，表明新方法相比于传统方法可提取更多的变形量，与原始序列更接近。从均方根误差来看，3个方向上，新方法与小波去噪方法相比分别减少47.37%、36%和40%，与EMD方法相比分别减少6.86%、2.31%和5.97%，表明新方法的去噪效果更稳定，能更清晰地表达变形趋势。

4 结 语

本文构建了一种自适应完备集合经验模态分解的去噪方法，引入排列熵理论确定高低频分界值K。该方法结合多种方法的优点，可有效解决EMD分析的端点效应和模态混叠问题，通过排列熵理论准确划分高低频，对高频噪声进行精细处理，使其GNSS变形监测的真实信息得到有效保留。仿真和实测数据实验表明，CEEMDAN方法的去噪精度显著优于EMD和小波去噪方法，证明了其有效性和可靠性。