基于向量旋转的拟合空间圆方法研究

张振虎

上海勘察设计研究院（集团）有限公司 上海 200082

引言

随着科技的发展、信息技术的进步，以及精密工程技术的发展，产生了很多新的测量技术，三维测量建模技术就是时代的产物。在核电厂、光源储存环、离子加速器实验装置等项目建造过程中，三维设计、设备制造、核心设备精密安装及重要设备在线监测均进行了大量建模，建模技术的采用促使高精度测量工作日益转向可视化、智能化及精密化。逆向建模作为一种最常用的建模方法得到了越来越广泛的应用，它主要通过激光扫描、激光跟踪或摄影测量等技术，获得目标物体的三维测量数据，然后根据测量数据构建三维高精度模型。以核电厂为例，其在建造过程中采用了激光跟踪技术对一回路主要设备，如反应堆压力容器、蒸汽发生器、主泵、主管道及波动管等进行了精密建模，这些设备的接口多为圆形，而这些设备接口的圆形并不在严格的水平面上，因此，对这些设备建模通常需要对空间圆进行拟合。

1 数学模型及算法

空间圆无直接公式描述，基于公式拟合的方法很难实施，故空间圆参数拟合一般采取间接方式进行。根据参考文献[1-5]，拟合空间圆主要采用平面与圆球相截法。由圆球性质可以得知，任何一个平面与圆球相截得到的截面均为圆形，故平面与圆球相截法是通过拟合平面与圆球得到空间圆参数。其中，文献[1-4]采取拟合平面和一个圆球中心位于拟合平面上的圆球得到空间圆参数；文献[5]也采取拟合平面和圆球方式进行，该方法不要求圆球圆心位于拟合平面上，在平面和圆球拟合后将球心投影到拟合平面上以得到圆心，过程较文献[1-4]复杂。拟合空间圆需要确定7个参数，包括空间圆所在平面的法向量(a，b， c)、空间圆的圆心(x0， y0， z0)和空间圆的半径R。本文通过拟合平面求取平面法向量，构建旋转矩阵，然后将空间圆拟合问题转化为平面圆拟合问题。在工程实例中，圆形截面的特征数据采集通常采用全站仪、激光扫描仪或激光跟踪仪完成。部分物体圆形截面因受视线阻隔往往难以一次测量就采集到所有特征数据，通常需要转站1～2次完成。转站需要进行大角度坐标转换，故在拟合空间圆前需要将多站的采集数据转换到同一个坐标系中。

综上，本文算法主要分为以下五步：①大角度坐标转换；②拟合空间圆所在平面求取平面法向量；③根据平面法向量构建旋转矩阵；④将拟合坐标点旋转，求取平面圆圆心和半径；⑤平面圆圆心旋转得到空间圆圆心。

1.1 大角度坐标转换

坐标转换模型可表示为：

其中，（X'、Y'、Z'）为转换前坐标，（X、Y、Z）为转换后坐标，λ为尺度系数，R为含三个旋转角α、β、γ的旋转矩阵，△X、△Y、△Z为平移参数。R=RxRyRz，Rx是把原坐标绕X轴旋转α角得到的旋转矩阵，Ry是把原坐标绕Y轴旋转β角得到的旋转矩阵，Rz是把原坐标绕Z轴旋转γ角得到的旋转矩阵，α、β、γ均为绕轴逆时针旋转。

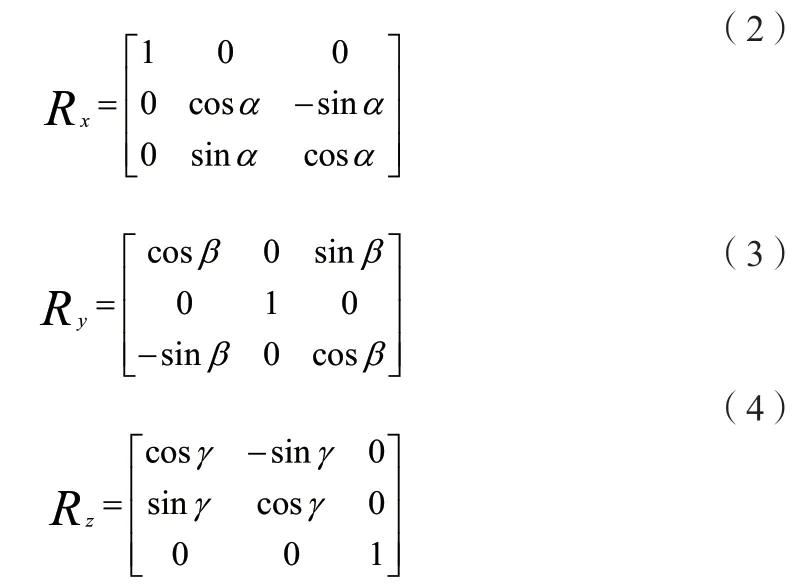
整理以后，旋转矩阵R为以下形式：

两坐标系之间转换需要求取7个转换参数，一般需要三个以上的公共点坐标来进行转换。

为便于数据处理，一般需要对所使用的公共点坐标进行重心化处理，将两套坐标系的坐标均转化为重心化坐标。根据参考文献[8]，重心化坐标计算公式如下：

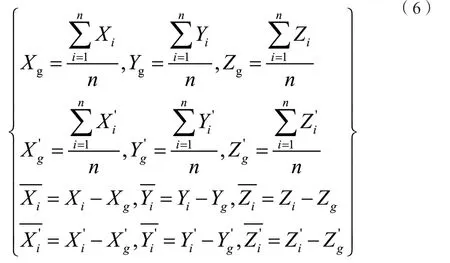
将公共点的中心化坐标代入式（1），可得：

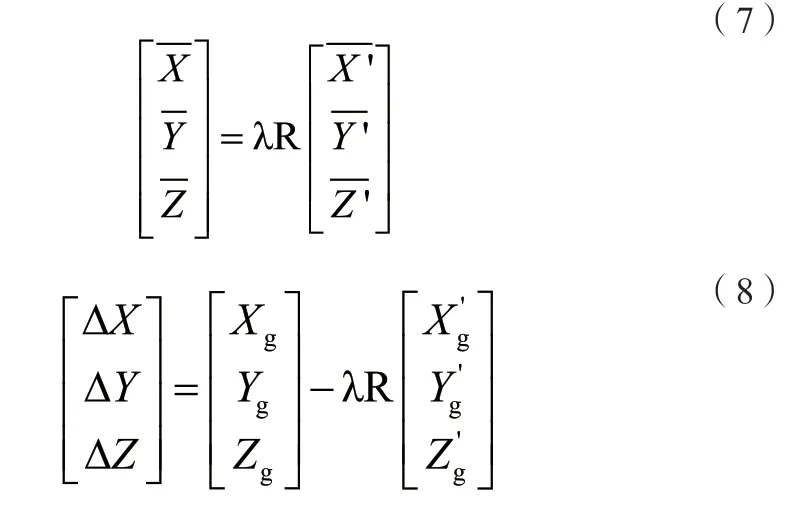
从上式可以看出，坐标转换参数计算时需要先计算尺度系数和旋转矩阵，然后代入式（8）就可以得到平移参数。

根据参考文献[9]，对式（7）两边取2-范数，由于R为正交矩阵，及λ＞0，可得

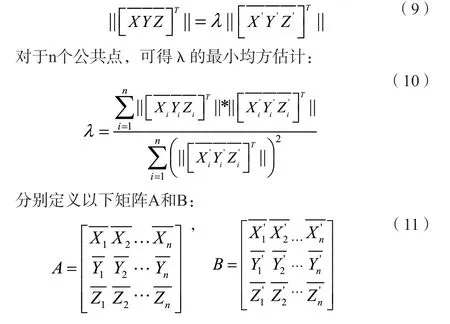
式（7）变化为以下形式：

求取正交矩阵R，使A-λRB的Frobenius范数最小时所得的R即为最佳转换矩阵，即求解以下问题：

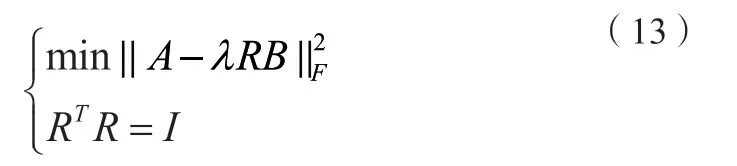
将上式进行迹函数计算并展开，得：

根据参考文献[6]，当且仅当R =VUT时，式（14）得到极小值。得到旋转矩阵后，将旋转矩阵代入到公式（8），就可以得到平移参数。

1.2 平面法向量计算

将所有坐标采集数据转换至同一坐标系后，就可以开始计算空间圆所在平面的法向量计算。

平面方程一般可表示为：

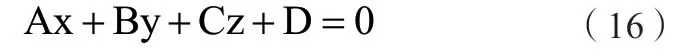
为减少参数的计算，可以将方程简化，两侧同除以D（D≠0），方程可以简化为：

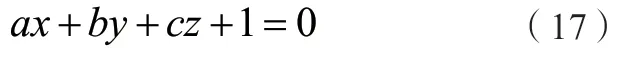
因方程的三个参数之间存在着线性关系，故可以采用求解线性方程组参数的方法进行结算。假设空间圆上的n个观测点为( xi， yi， zi)（1≤i≤n），以矩阵形式表示如下：

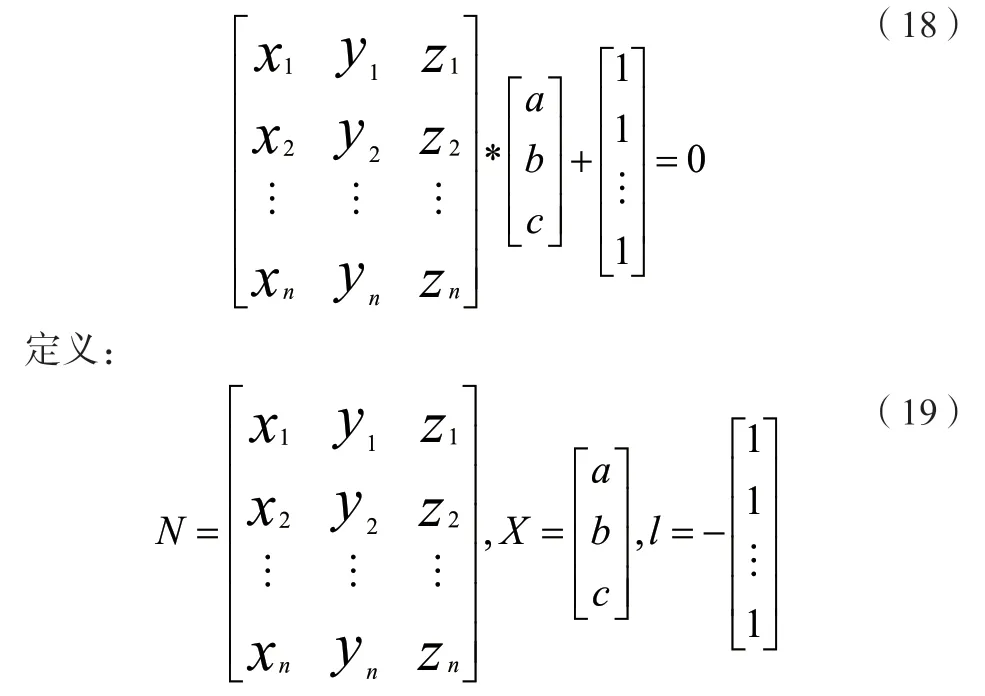
上式可以简化为：

其最小二乘解为：

上述算法为拟合平面最常用算法，但该算法并未考虑系数矩阵N 中存在的误差，且造成了固定项l 中数据的改动，得到的结果必然不是最优的。

假设系数矩阵N中存在独立同分布误差，根据参考文献[6]，其参数求解可以采用以下算法。

将( xi， yi， zi)重心化，得到重心坐标重心化公式如下：

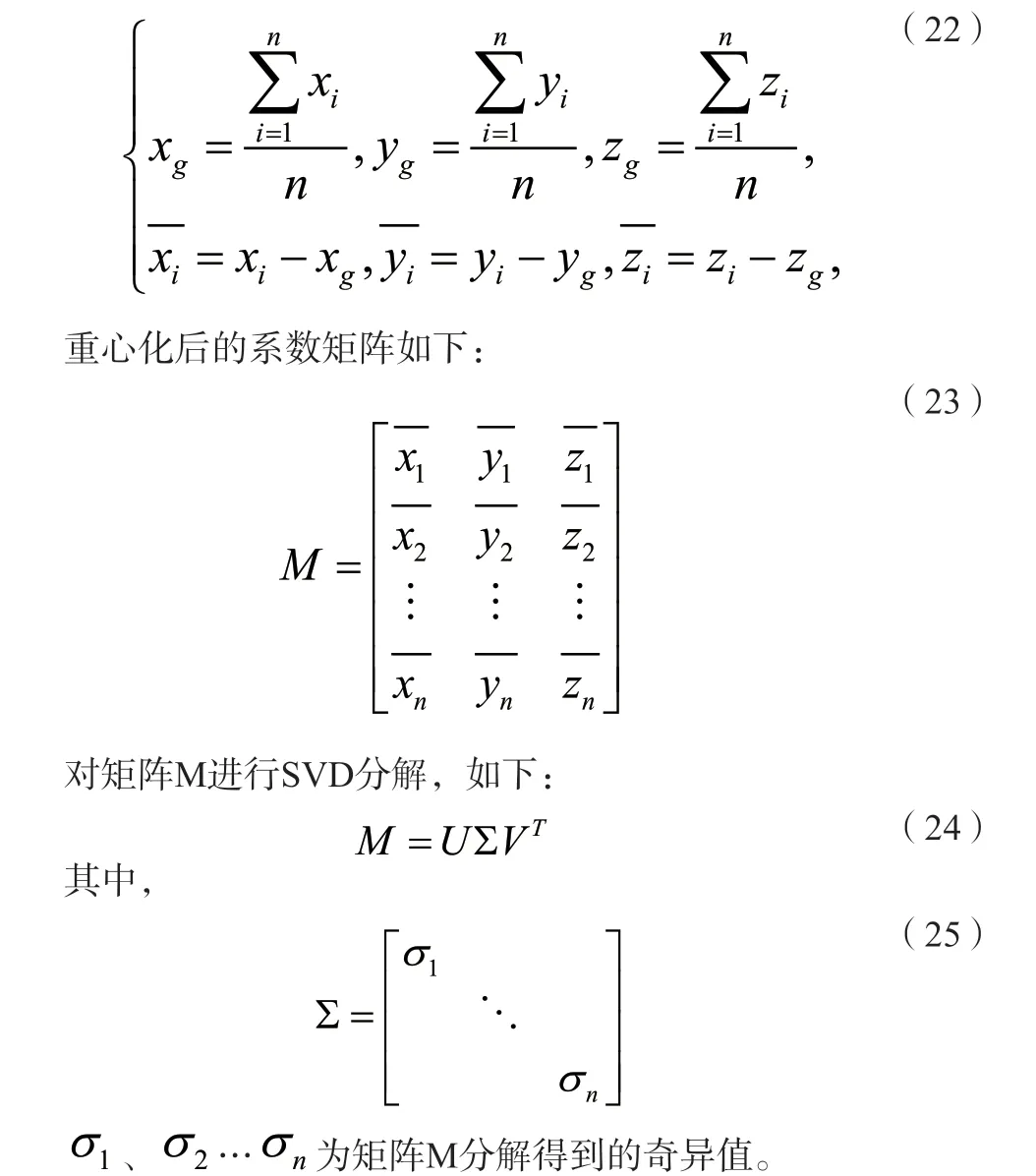
最小奇异值所对应的V向量[ a 'b ' c ']T即为平面方程中参数A、B、C的值。平面方程中常数项的值可按下式计算：

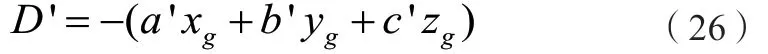
根据文献[7]研究，基于奇异值分解的拟合平面方法与基于正交距离拟合平面的方法是等价的，其求得的平面参数可以使点到平面的距离平方和最小，其比式(18)—(21)采用的拟合平面常用算法更为精确。

1.3 求取圆心和半径

（1）构建旋转矩阵

假设空间圆的圆心坐标为( x0， y0， z0)，其应位于拟合的平面上，故有：

应用罗德里格旋转公式矩阵形式，将平面法向量旋转至与Z轴平行，其构成的旋转矩阵如下：

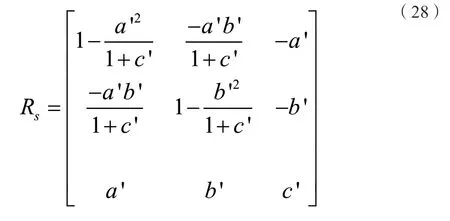
其旋转公式表达为：

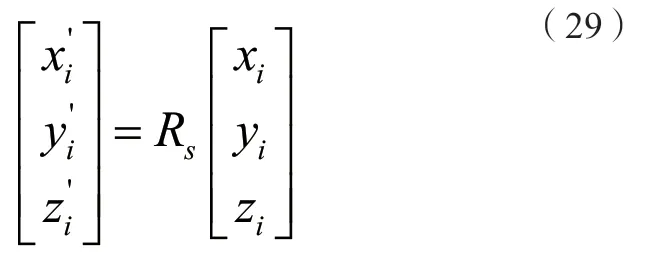
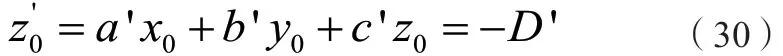
（2）拟合平面圆

平面圆方程可以用下式表示：

采用最小二乘法可以得到E、F、G的值，平面圆圆心及半径值计算如下：

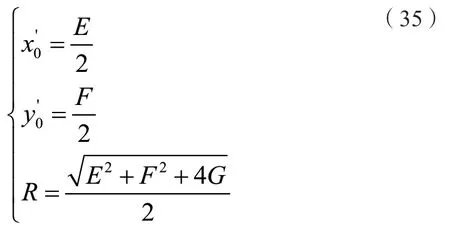
（3）解算空间圆圆心

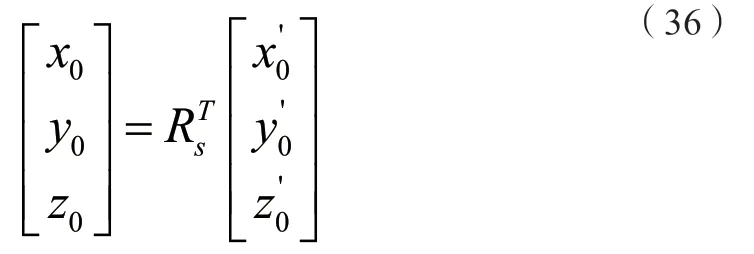
1.4 拟合空间圆效果评价

计算拟合点到空间圆的法向偏差：

计算拟合点到拟合圆的径向偏差：

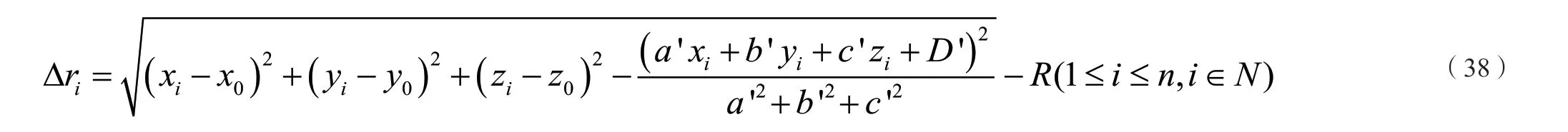
计算拟合点到拟合圆的空间偏差：

计算RMSE（均方根误差）：

2 工程算例

某设备中部的法兰需要与其他设备法兰进行精密对接，为检测设备的匹配性，需要在安装前进行模拟对接。为精确模拟，采用激光跟踪仪对设备的法兰圆面进行了测量。因视线阻挡，难以在一站就完成所有数据的采集，故法兰圆面的测量采取了转站测量的方式，两站之间采用公共点进行连接。采集的原始数据请见下表1。

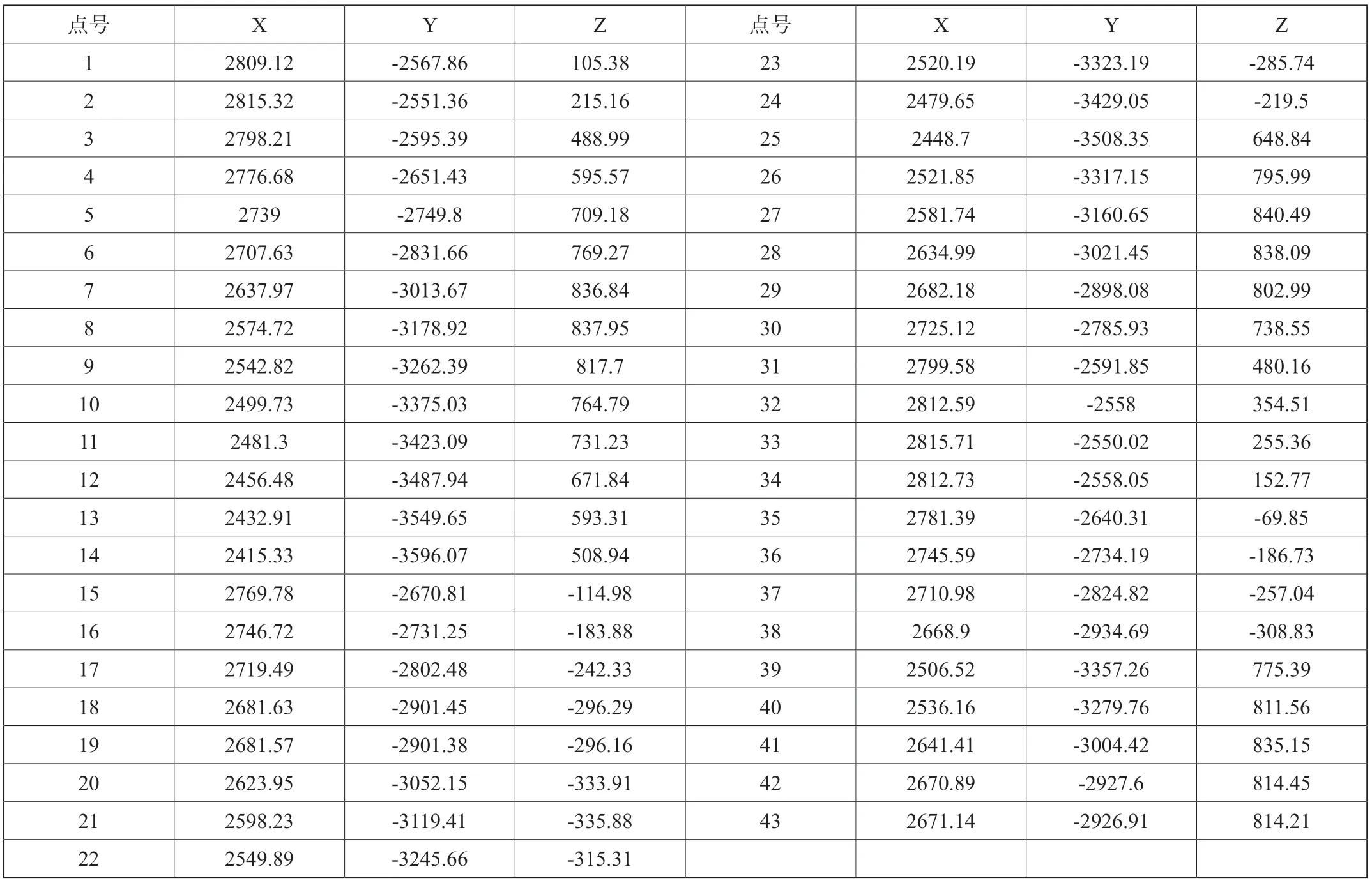
表1 某设备中部法兰圆第一站测量数据（单位：mm）

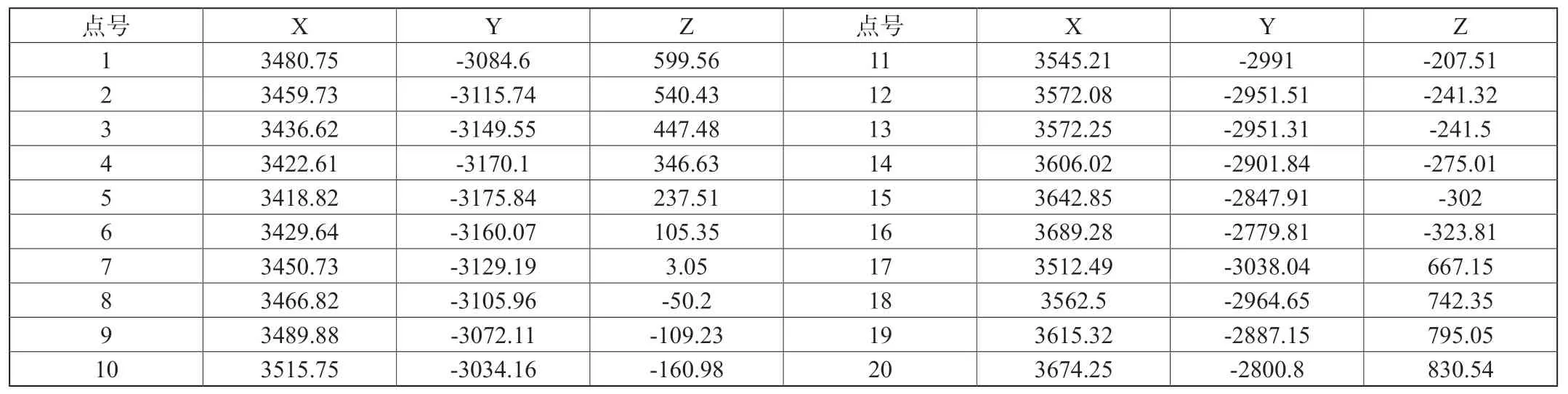
表2 某设备中部法兰圆第二站测量数据（单位：mm）

表3 公共点测量数据（单位：mm）

表4 坐标转换参数

采用本文坐标转换算法，计算第二站转入第一站的坐标转换参数。因激光跟踪仪的精度很高，且测量距离较短，其坐标转换尺度系数可视为1。计算出来的旋转矩阵及平移参数请见表4。

利用表4的坐标转换参数将第二站的测量数据转入到第一站测量坐标系中，并计算拟合圆的参数。根据本文算法，对空间圆的数据进行了拟合，拟合后的平面方程单位法向量为（0.93393557，-0.357440912，0.000587606），平面方程常数项为-3541.36949，空间圆圆心坐标为（2605.2329，-3100.094608，253.8655206），半径为589.6816919mm。根据拟合结果计算出的拟合后各点的法向偏差、径向偏差及空间偏差见表5。

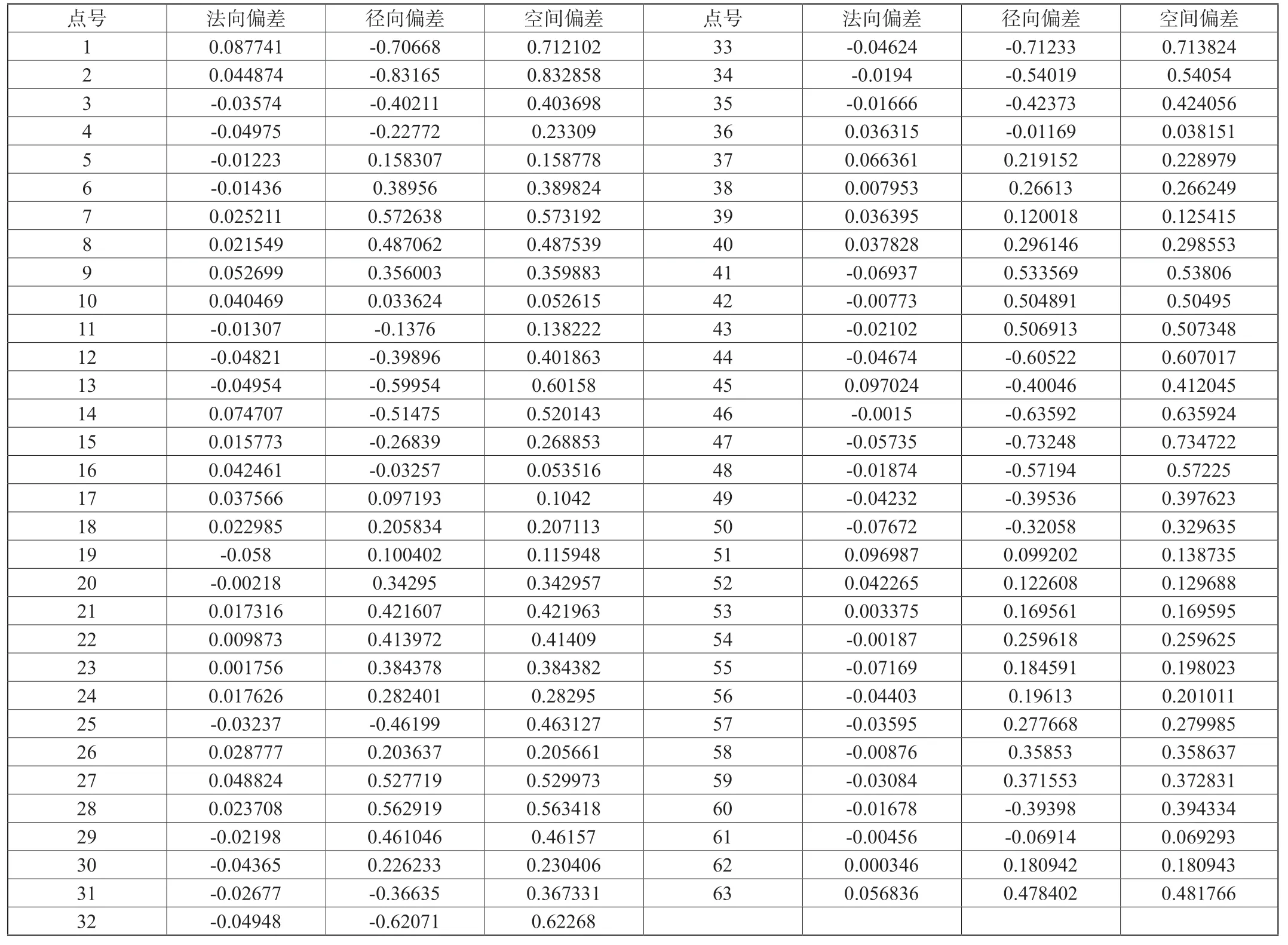
表5 某设备端面圆拟合后偏差统计（单位：mm）

采用式(40)，根据表5中所示的各点的法向偏差、径向偏差及空间偏差计算均方根误差（RMSE）。经计算，法向偏差RMSE为0.042167mm，径向偏差RMSE为0.409195mm，空间偏差RMSE为0.411362mm，说明拟合圆的各项偏差均很小，空间圆参数解算较准确。

为验证本文中算法，使用文献[2]中的算法对本文数据进行拟合。为便于拟合后参数的对比，本文将采用文献[2]中算法解算出的平面法向量进行了单位化。文献[2]中算法和本文算法解算的结果如表6所示。

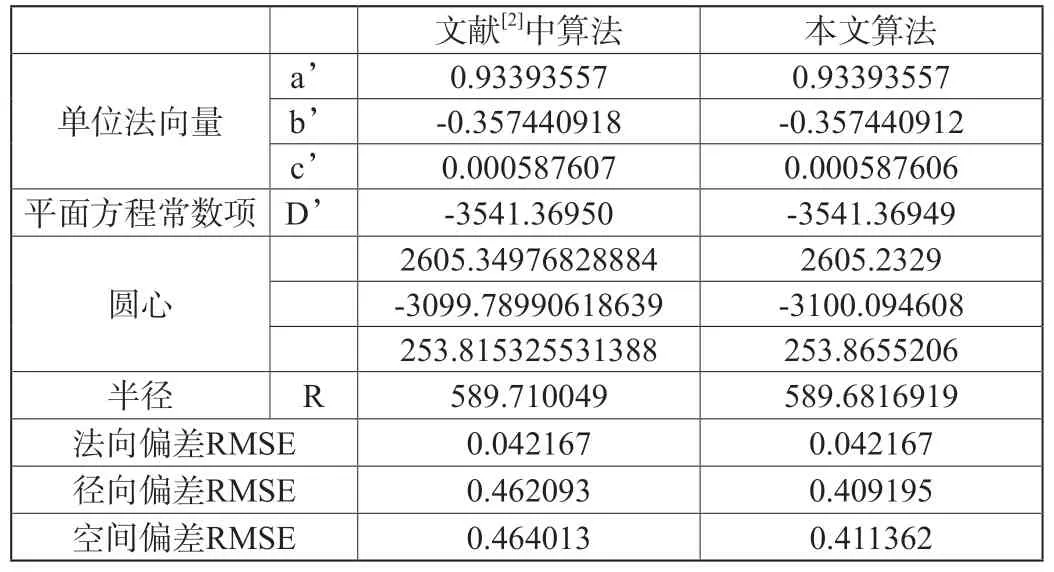
表6 文献[2]算法和本文算法解算结果（单位：mm）

通过表6可发现，本文所述算法拟合空间圆后法向偏差RMSE和文献[2]中使用的算法结果基本一致，但径向偏差RMSE及空间偏差RMSE均略优于文献[2]中使用的算法，说明本文算法可行，精度较高。

3 结束语

本文通过奇异值分解法拟合平面，构建旋转矩阵化空间圆拟合为平面圆拟合，原理清晰，不用进行迭代，且有利于编程计算，并通过实践证实，该方法实用且可靠。适合用于核电厂、光源存储环实验装置、直线加速器实验装置、飞机、造船、汽车、航空航天等行业大型设备模型构建过程中圆形截面的拟合。