双悬臂L 型预应力混凝土盖梁受力特点及配束方法

陈振东

［上海市政工程设计研究总院（集团）有限公司，上海市 200092］

0 引 言

随着桥梁快速化施工的越来越普及，常采用预制化的上部结构与盖梁相结合的桥梁形式。同时为节约城市空间，减少桥梁下部结构的占地面积，盖梁常设计成双悬臂的形式，关于双悬臂盖梁的设计，许多文献都进行了详细的分析阐述，如不同钢束线型对于盖梁结构受力的影响[1]，盖梁的施工过程分析[2]等，均为双悬臂盖梁的设计提供了较好的参考。然而，上述文献中所提及的盖梁大多是平头盖梁或截面横向对称的倒T 型盖梁，对于工程中常会碰到的L 型截面盖梁，探讨分析较少。本文以上海市大叶公路奉贤段改建工程中的工程实例为背景，对双悬臂L 型预应力混凝土盖梁的受力特点进行深入分析，总结此类型盖梁的钢束配置方法及施工阶段的钢束张拉顺序布置，以期为往后工程设计提供一些参考。

1 工程概况

上海市大叶公路奉贤段改建工程全长约31 km，工程范围内有较多跨路口、跨航道的节点，中跨选择双主梁型式的简支叠合梁进行跨越，边跨采用预制预应力混凝土小箱梁。由于叠合梁不设置牛腿，2 种主梁结构间的分界墩需采用高低盖梁设计。本文选用案例中叠合梁跨径62 m，梁高3.1 m；边跨小箱梁跨径35 m，梁高1.9 m；盖梁两侧高差达到了1.1 m，盖梁构造如图1 所示。该盖梁结构异型，属于较为特殊的高低盖梁形式，本文将这种盖梁型式描述为L 型盖梁。

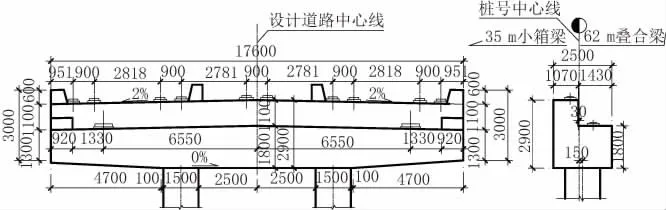
图1 L 型盖梁构造图(单位：mm)

2 预应力钢束配置方案

2.1 配束方案

方案一：钢束横向对称于盖梁型心，贴近较低一侧盖梁顶缘布置，该种布置形式钢束相对于盖梁型心的偏心弯矩矢量方向与X 轴平行，即盖梁所受弯矩合力均为竖向弯矩。

方案二：将盖梁截面内钢束分为2 批，分别贴近高侧盖梁顶和低侧盖梁顶布置，该种布置形式钢束相对于盖梁型心的偏心弯矩矢量方向与X 轴存在一定的夹角，且盖梁高差越大，夹角越大，即盖梁除受到竖向弯矩以外，同时还需承受钢束横向不对称布置产生的水平向弯矩。

2 种配束方案见图2。

2.2 2 种配束方案空间受力分析

本文采用Abaqus 软件建立空间实体有限元模型，对上述2 种配束方案下的L 型盖梁进行受力分析，对比2 种方案下盖梁的应力分布、盖梁结构尺寸、材料用量差异。

L 型盖梁实体有限元计算模型见图3。

结构分析荷载组合统一选用标准组合：（1.0×一期恒载+1.0×二期恒载+1.0×活载（含冲击系数）+1.0×温度）；使用阶段应力控制要求：压应力σc≤16.2 MPa ，不出现拉应力。按照上述荷载组合及应力控制要求，可满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）的规定。

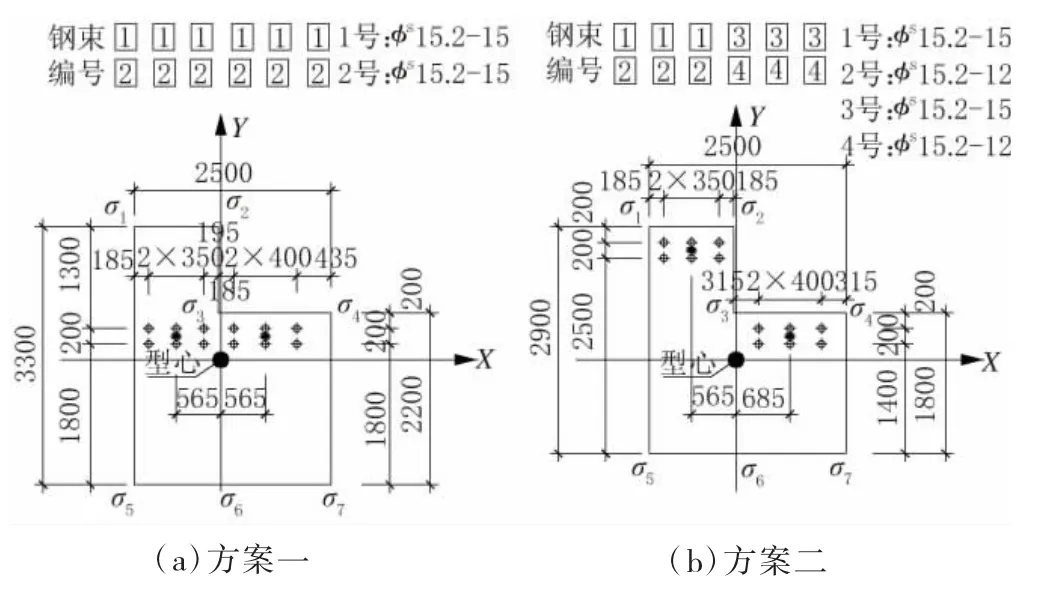
图2 2 种配束方案

图3 L 型盖梁实体有限元计算模型

为描述盖梁应力沿截面横向（Z 向）的分布情况，选取盖梁截面上7 个点的应力作为研究对象，对应应力依次定义为 σ1、σ2、σ3、σ4、σ5、σ6、σ7、，见图2。2种配束方案下各点的应力迹线如图4~ 图9 所示(图中Z 为沿盖梁横向的坐标)。

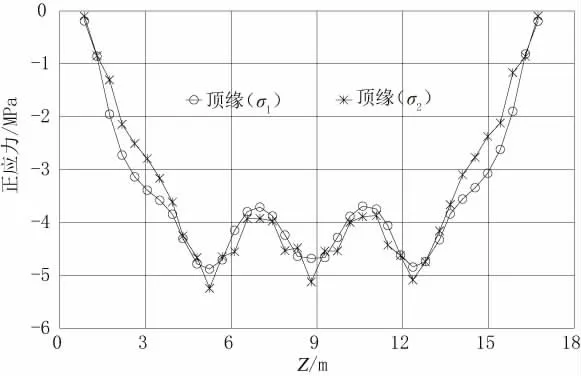
图4 方案一盖梁顶缘应力迹线图（σ1、σ2）

由图4、图6、图8 可见，方案一的盖梁沿截面横向应力分布较均匀。但由于钢束离型心偏心距较小，钢束利用率不高，盖梁满足应力控制要求时，需要采用更高的梁高。

由图5、图7、图9 可见，方案二的盖梁沿截面横向应力分布较不均匀。但钢束离型心偏心距较大，钢束利用率高，相对方案一，可采用更小的梁高和更少的钢束。

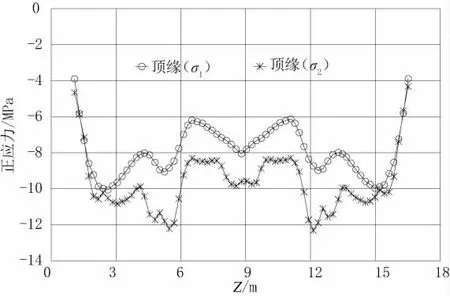
图5 方案二盖梁顶缘应力迹线图（σ1、σ2）

图6 方案一盖梁中缘应力迹线图（σ3、σ4）

图7 方案二盖梁中缘应力迹线图（σ3、σ4）

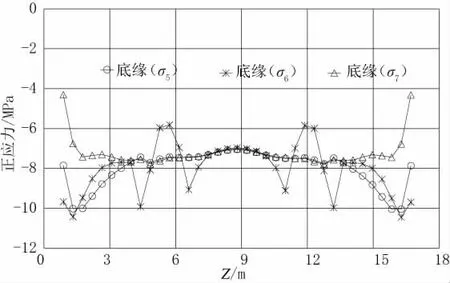
图8 方案一盖梁底缘应力迹线图（σ5、σ6、σ7）

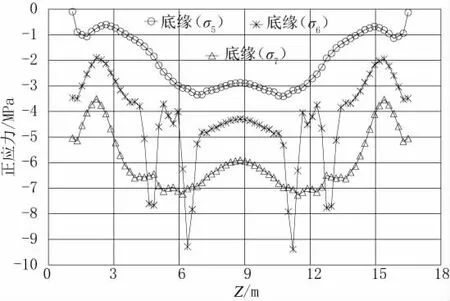
图9 方案二盖梁底缘应力迹线图（σ5、σ6、σ7）

方案一、二的构造尺寸、材料指标对比如表1 所示。由表1 可见，当采用方案一的配束方案时，混凝土用量增加19%，钢束用量增加11%，钢筋用量增加14%。

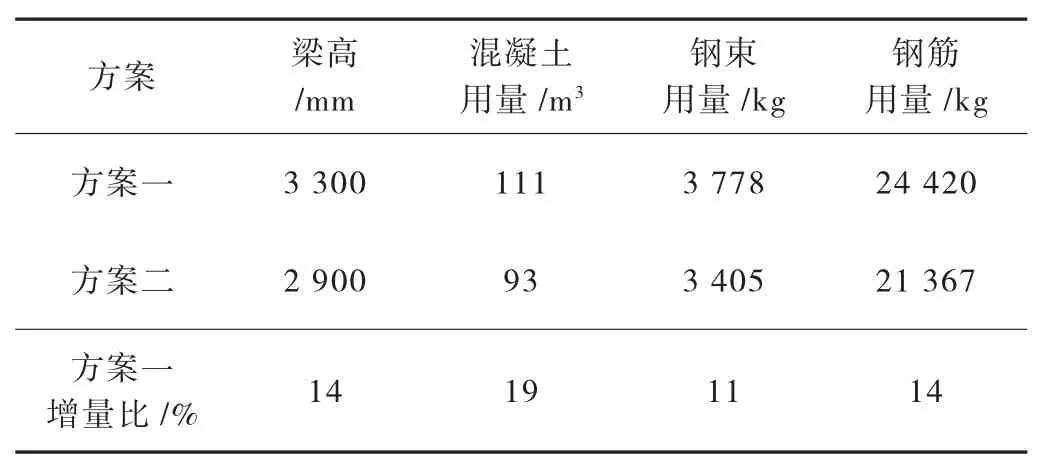
表1 方案一、二设计指标对比表

根据2 种方案的应力分布和设计指标对比可得如下结论：

（1）2 种方案均可满足应力控制要求，方案一沿盖梁横截面的应力分布较方案二均匀，受力情况更好。

（2）方案一的盖梁梁高较高，体量大，景观效果较方案二差。

（3）方案一的盖梁材料用量较多，经济性较方案二差。

综上，方案二景观效果和经济性均较方案一好，针对本文描述的整体梁高较高、截面两侧高差较大的L 型盖梁，方案二为更优的选择。而方案一可用于盖梁所受顶缘负弯矩较小或盖梁截面两侧高差不大的情况。

由图5、图7、图9 可见，方案二盖梁横截面的应力总体分布趋势为：梁高较低一侧压应力较大，梁高较高一侧压应力较小，盖梁横向受弯，截面横向应力分布不均匀主要是由于钢束横向不对称布置导致，可通过优化钢束布置来减轻盖梁应力沿截面横向分布不均的情况。

3 横向不对称钢束配置方案优化

优化后的横向不对称钢束布置图见图10。

如图10（a）所示，将盖梁断面型心轴（Y 轴）左侧钢束总面积定义为A1，右侧钢束总面积定义为A2，左侧钢束合力点到型心水平距离为B1，右侧钢束合力点到型心水平距离为B2。上节中，按照通常的盖梁钢束布置方法，取A1=A2，B1（565 mm）＜B2（685 mm），盖梁存在横向受弯效应，矩矢沿Y 轴正向，即应力点1~应力点5 侧受拉。可采取以下2 种方法减轻盖梁横向受弯效应：

（1）减小A2值，即减少Y 轴右侧钢束布置。

（2）减小B2值，即减小Y 轴右侧钢束合力点至盖梁型心距离。

为便于统一配束原则，本文取B2=B1，在此基础上减少Y 轴右侧钢束布置，优化后的钢束布置如图10（b）所示。Y 轴左侧布置 3 束 φs15.2-15 和3 束 φs15.2-12 钢束；Y 轴右侧布置 6 束 φs15.2-12钢束，钢束合力点到型心水平距离均为565 mm。

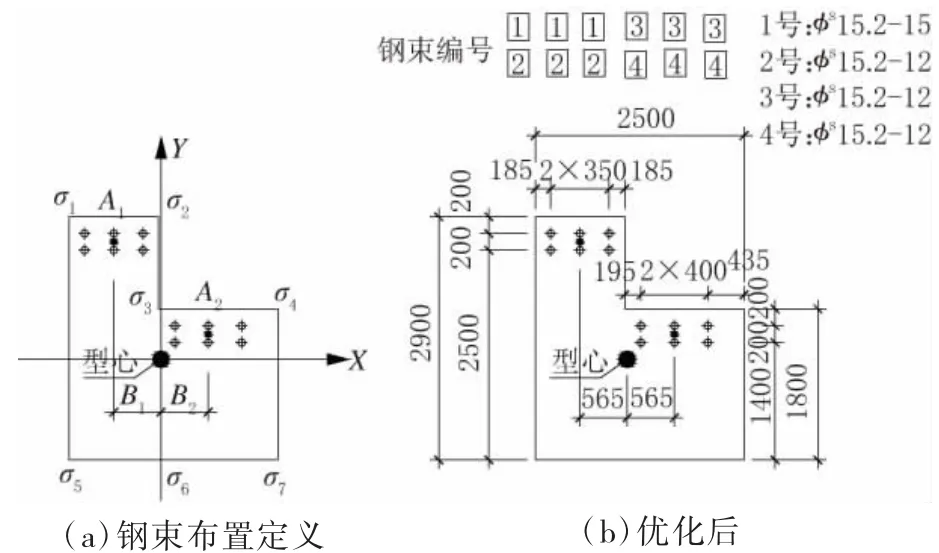
图10 优化后的横向不对称钢束布置图（单位：mm）

对优化后的盖梁设计方案进行空间实体有限元计算分析，并与同情况下的梁单元计算结果进行对比。盖梁各点的应力迹线图及梁单元模型应力计算结果如图11~ 图13 所示(图中 Z 为沿盖梁横向的坐标)。由图可见，盖梁顶、底缘应力沿截面横向分布较优化前均匀很多，顶缘同一点处的应力最大差值1.6 MPa，底缘（除立柱附近应力集中区域外）同一点处的应力最大差值2 MPa，盖梁中缘支座集中力作用区域集中应力由原15 MPa减小至12.1 MPa。盖梁整体受力情况得到较大改善。

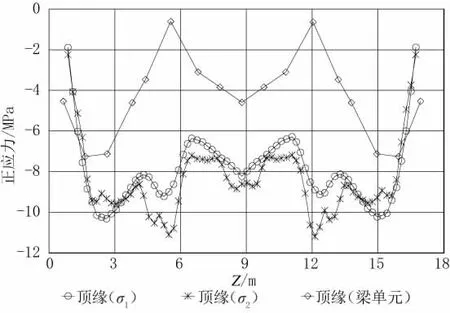
图11 优化后盖梁顶缘应力迹线图（σ1、σ2、梁单元）

此外，经过与梁单元计算结果的对比可知，梁单元模型计算所得盖梁顶缘应力与实体模型计算结果偏差较大，整体压应力偏小，立柱区域外压应力差值约3.6 MPa，立柱区域压应力差值约9.6 MPa。而盖梁底缘应力与实体模型计算结果偏差较小，立柱区域外压应力差值约1 MPa。立柱区域内，盖梁底缘与立柱边缘的折角区域存在应力集中效应，最大压应力9.525 MPa，见图14。梁单元模型未能模拟应力集中效应，相应位置最大压应力为7.710 MPa，大于应力集中区域外的应力5.7 MPa。

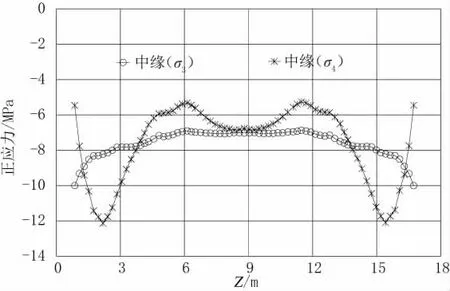
图12 优化后盖梁中缘应力迹线图（σ3 、σ4）

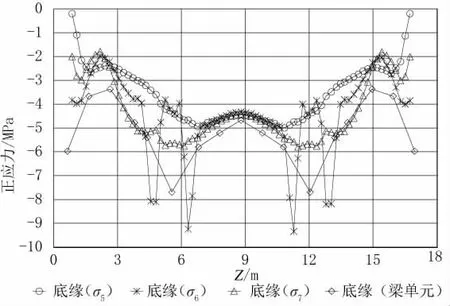
图13 优化后盖梁底缘应力迹线图（σ5、σ6、σ7、梁单元）

图14 盖梁底缘立柱区域应力集中效应（单位：P a）

经分析，2 种计算模型下结果存在偏差的原因主要有以下2 点：

（1）梁单元模型未能准确模拟立柱宽度对于盖梁顶缘弯矩的折减效应，导致顶缘压应力计算结果偏小，底缘压应力偏大（除应力集中区域外）。

（2）本文所研究的L 型盖梁实际受力情况已偏离平截面假定[3]，尤其在立柱附近区域存在较大的集中应力，以平截面假定为基础的梁单元计算模型未能准确模拟。

综上，本节所描述的盖梁配束优化方法能较好地改善L 型盖梁的受力情况。对于L 型盖梁的配束，采用经过优化的横向不对称钢束配置方案，从经济性和景观效果上均更佳。

对于本文所研究的L 型盖梁，梁单元计算模型的分析结果与盖梁真实受力情况存在偏差，但整体计算结果基本满足应力控制要求。实际工程中可利用梁单元模型进行盖梁的初步配束，再建立实体有限元模型进行配束的复核和优化。

4 施工阶段分析

盖梁的配束设计，除满足使用阶段的盖梁受力需求外，还需合理安排钢束的张拉批次及顺序，以满足施工过程中的盖梁受力需求。本工程将盖梁钢束分为2 个批次张拉，施工过程分为如下几个阶段：

（1）浇筑盖梁混凝土，待盖梁混凝土达到设计强度时张拉第1 批钢束，拆除盖梁支架，盖梁主体施工完成。

（2）吊装上部结构。

（3）上部结构吊装完成后张拉第2 批钢束。

（4）施工桥面铺装、防撞护栏等附属设施。

第1 批次张拉的钢束，需同时满足阶段1 和阶段2 盖梁的受力需求。根据前文所述的L 型盖梁受力特点，第1 批钢束的布置，可按照第3 节中所述的A1＞A2的原则进行，见图15。盖梁各阶段的主要应力分布如表2 所示，4 个阶段的盖梁应力均可满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 3362—2018）要求，其中阶段1 中下缘拉应力较大，需适当加强盖梁下缘的纵向普通钢筋配置。

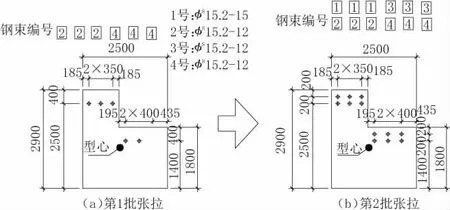
图15 施工阶段钢束张拉顺序（单位：mm）

5 结 语

（1）横向不对称钢束配置方案用于L 型盖梁的经济性和景观效果均较好，推荐采用。由于钢束横向不对称布置导致的沿盖梁截面横向应力分布不均匀，可通过调整钢束相对盖梁截面型心的横向位置和型心两侧的钢束布置比例进行优化。

（2）施工过程中不同的钢束张拉批次下，L 型盖梁同样会出现沿截面横向应力分布不均的情况，应重视施工过程中钢束张拉顺序的分配，保证盖梁满足短暂状况下的应力控制要求。

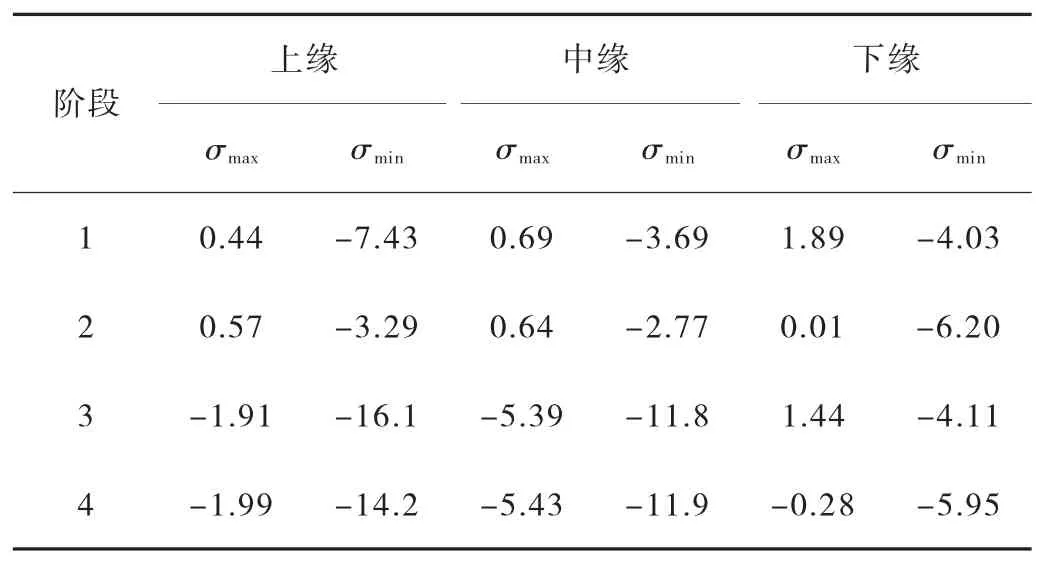
表2 施工阶段盖梁主要应力 单位：MP a

（3）由于L 型盖梁的受力状态已偏离平截面假定，设计过程中常使用的梁单元模型计算结果不能准确模拟盖梁的真实受力状态。设计过程中可采用梁单元模型进行盖梁的初步配束，然后建立更准确的空间实体有限元模型进行盖梁的受力分析及配束优化。