基于先验知识的头颈部肿瘤调强放疗计划多目标优化方法
刘劲光,刘国才
1.湖南大学电气与信息工程学院,湖南长沙410082;2.湖南工程学院计算科学与电子学院,湖南湘潭411104
前言
恶性肿瘤严重威胁人们的生命健康,手术、放疗和化疗是3 种临床上主要的治疗方法。放射治疗因其适应证广泛、疗效较好,在肿瘤的治疗中有着无可替代的重要地位。据报道大约有70%的恶性肿瘤病人需要接受放疗,在美国、日本等国家,接受放疗者约占当年新发病例的50%~60%,目前仍有上升趋势。放射治疗的主要目标是使肿瘤靶区(包括GTV、CTV、PTV)接收到足够的高能辐照剂量以彻底消灭肿瘤细胞,同时又要使肿瘤周边的正常组织受到尽可能小的照射剂量,以最大限度地避免正常组织受到损伤,减少放疗副作用。目前临床上广泛采用的逆向调强放疗计划(IMRT)是使照射的剂量在整个肿瘤靶区内按照处方剂量形成梯度分布,同时又要使周边的危及器官(OAR)满足相应的临床剂量约束条件。因此,肿瘤IMRT 计划本质上是一个多目标优化问题,但因该多目标优化问题的目标函数很多(头颈部肿瘤通常有20多个),且待优化的参数个数非常多(通常大于1 000 个),目前没有精确求其Pareto 最优解集(Pareto optimal solution set)的有效方法。临床上通常将多目标的IMRT 计划优化问题转化为单目标优化问题求解,寻找临床上可接受的次优解。目前临床上IMRT计划通常采用两步优化方法[1]:
步骤1:临床放射物理师根据各靶区及其危及器官的临床剂量约束条件构造一组适当的目标函数fi,i=1,2,…,n,并根据经验对每个目标函数赋予适当的权重wi,i=1,2,…,n,将这组目标函数加权求和形成一个单目标优化问题。通过优化该单目标可以获取各照射野的强度分布或通量图,这一步也称为通量图优化(Fluence Map Optimization,FMO)。
步骤2:将各方向照射野的通量图分解为一组临床上医用直线加速器可执行的照射子野或口径的加权叠加,各子野的形状由多叶准直器(MLC)形成。各子野的权重通常称为子野机器跳数(MU),由直线加速器的出束率与出束时间实现。
两步优化的主要优点是第一步的优化过程,即通量图优化,其目标函数是凸函数或可转化为凸函数,可利用很多方法求解。通量图优化模型如下:

其中,X是待优化参数向量,表示各射野单元野的权重,即照射强度,在区域Ω 内取值。D是剂量贡献矩阵,其元素Dij表示单位强度照射下的第i个单元野对第j个体素剂量沉积的贡献大小。d是空间感兴趣区域的剂量分布向量。由于权重因子wi,i=1,2,…,n,无直接临床意义,仅用于调整各目标函数的相对重要程度,故要选择一组合适的权重因子非常困难,需要设计者在计划优化过程中根据剂量分布的情况和剂量体积直方图等对优化结果进行可视化评估,多次修正权重因子并反复优化,直至找到临床可接受的放疗计划为止。
为了避免多次修正模型(1)中的权重因子,可直接求解多目标优化模型(2),即多个目标函数同时最优化并选取最优解。
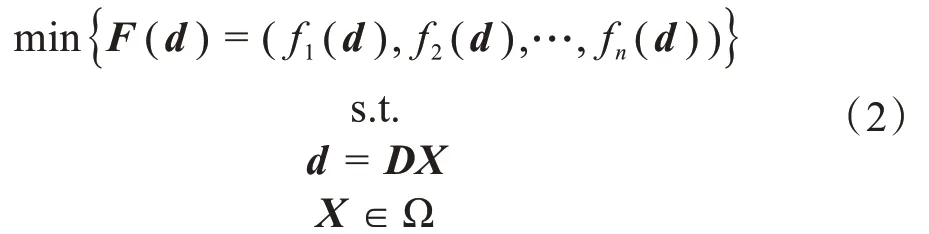
多目标优化的目的是使各目标函数同时最优,达到最小值。然而由于各目标函数间的相互冲突,一般情况下不可能所有目标函数同时达到最小。因此,工程上通常求其Pareto 最优解集[2]。任何一个Pareto 最优解均满足条件:如果其中某个目标函数值减小,则必定导致至少一个其它的目标函数值增大。全体Pareto 最优解所对应的目标函数值集合构成了目标函数值空间的一个Pareto前沿。
目前逼近Pareto前沿的方法较多,主要有夹心算法和进化算法两大类[3-4]。若所有目标函数都是凸函数,则可以采用夹心算法[5-6]逼近多目标优化问题(2)的Pareto 前沿。由凸分析理论[7]可知,在Pareto 前沿上可逐步选取一组适当的点,这组点称为锚点,连接这组锚点所构成的超凸多边形成为Pareto 前沿的一个“上界面”,而由通过这组锚点的切平面所构成的超凸多边形成为Pareto 边界的“下界面”,Pareto 前沿被“夹在”以上两个“上、下界面”之间。因此,这两个“上、下界面”之间的最大距离可用来度量它们逼近Pareto前沿的程度。
当找到Pareto 前沿后,IMRT 计划设计者只要通过可视化的导航便可以选出临床上最优的Pareto解[8-9],即最优的临床放疗计划。因此,逼近Pareto 前沿是多目标优化的核心。但是直接逼近模型(2)中的Pareto 前沿一般比较困难,其原因主要有几点:首先,目标函数的个数较多,特别对头颈部肿瘤,模型(2)中的目标函数往往超过20 个。由于逼近Pareto前沿所需要的锚点个数随目标函数的增加呈指数增长并且收敛速度也会随目标函数的增加而变慢,因此,对头颈部肿瘤的多目标优化问题,直接逼近Pareto 前沿几乎无法实现;其次,待优化参数X 的个数也非常大,头颈部肿瘤一般超过1 000。为减少计算量,提高优化速度,一方面可以重新定义多目标调强放疗计划优化的目标函数,通过减少目标函数的个数来降低Pareto前沿的维数;另一方面也可在优化过程中添加适当的约束条件[10],限定Pareto前沿的范围,即仅逼近有临床意义的部分Pareto前沿。但如何选取约束条件目前尚无具体标准,这是因为选取的约束条件如过于苛刻,有可能导致无满足约束条件的放疗计划,因而无法生成Pareto前沿;反之,如选取的约束条件过于宽松,可能导致生成的Pareto前沿过大,在逼近过程中需要确定更多的放疗计划[11],即需要更多Pareto前沿上的锚点。
已有文献表明肿瘤IMRT计划对同类肿瘤的新患者放疗计划设计具有一定的指导意义[12-13],如Chanyavanich等[12]将新的前列腺肿瘤病人与已有的100个前列腺病人样本影像进行匹配,找出影像互信息最大的样本,将该样本的放疗计划作为新病人的放疗计划。实验结果表明该方法能使靶区PTV受到的照射剂量与传统计划相当,同时对危及器官的保护程度也类似,但无需重新进行放疗计划的优化,因而基于先验信息的放疗计划优化比传统IMRT方法计算速度更快。此外,Tol等[13]也得到类似的结果。
本文首先根据同类肿瘤放疗剂量的先验知识,对各危及器官的线性EUD 按相关系数进行R 型聚类分析[14],将危及器官分为3类;其次,将所有属于同类危及器官的线性EUD 均值看作目标函数,联合肿瘤靶区的约束条件,构造了一个维度较低的多目标优化模型;最后,通过基于角解的增强夹心算法逼近该低维、局部的Pareto 前沿,并通过可视化导航方法确定一个实时的调强放疗计划。对比传统的多目标调强放疗计划优化,本文方法的创新点主要有两个:其一,通过对头颈部肿瘤的各危及器官进行R型聚类分析,并按类构造目标函数,显著减少了多目标IMRT计划优化的目标函数个数,降低了Pareto前沿的复杂度;其二,在逼近Pareto 前沿时提出了基于角解的增强夹心算法,能比原增强夹心算法生成更完整的近似Pareto前沿。实验结果表明,本文方法可以将头颈部肿瘤IMRT计划多目标优化模型中的20~21个目标函数减少到6~7 个,并能有效确定其近似的Pareto 前沿,找到与临床实际放疗计划质量相当、部分指标甚至更优的放疗计划。
1 基于先验知识的多目标IMRT计划优化
1.1 头颈部肿瘤IMRT计划优化靶区目标函数的构造
对肿瘤靶区,主要考虑均匀剂量、最大剂量和最小剂量3类约束条件。
参考Rivera 等[15-16]的目标函数构造方式,靶区目标函数定义为式(3):

其中Target 为计划优化时所考虑的靶区,如GTV、CTV、PTV。NTarget表示该靶区的体素总数,di为靶区第i个体素的剂量值。
1.2 头颈部肿瘤IMRT计划优化危及器官目标函数的构造
对头颈部肿瘤放疗计划优化,我们在计划设计过程中主要考虑Brain Stem、Left eye、Left lens、Right lens、Right eye、L_temporal lobe、R_temporal lobe、Left TM_joint、Right TM_joint、Spinal cord、Larynx、Mandible、Left optic nerve、Right optic nerve、L_parotid、R_parotid、Optic chiasm、Pituitary 共18 个危及器官,IMRT 计划目的是使肿瘤受到更高辐射剂量照射的同时,保证所有危及器官的并发症(Normal Tissue Complication Probability,NTCP)最小。而NTCP 可以看成等效均匀剂量(Equivalent Uniform Dose,EUD)的函数[17],EUD 又可进一步由危及器官剂量的平均值和最大值线性组合来拟合[8,18],即线性EUD。因此NTCP 最小本质上要求危及器官的线性EUD最小。我们采用线性EUD作为危及器官的目标函数,即

其中,αOAR为系数因子,其具体取值与危及器官的性质有关(表1),如对串行器官脑干、脊椎等,αOAR的取值较小,而对并行器官如双颞、腮腺等,αOAR的取值较大。
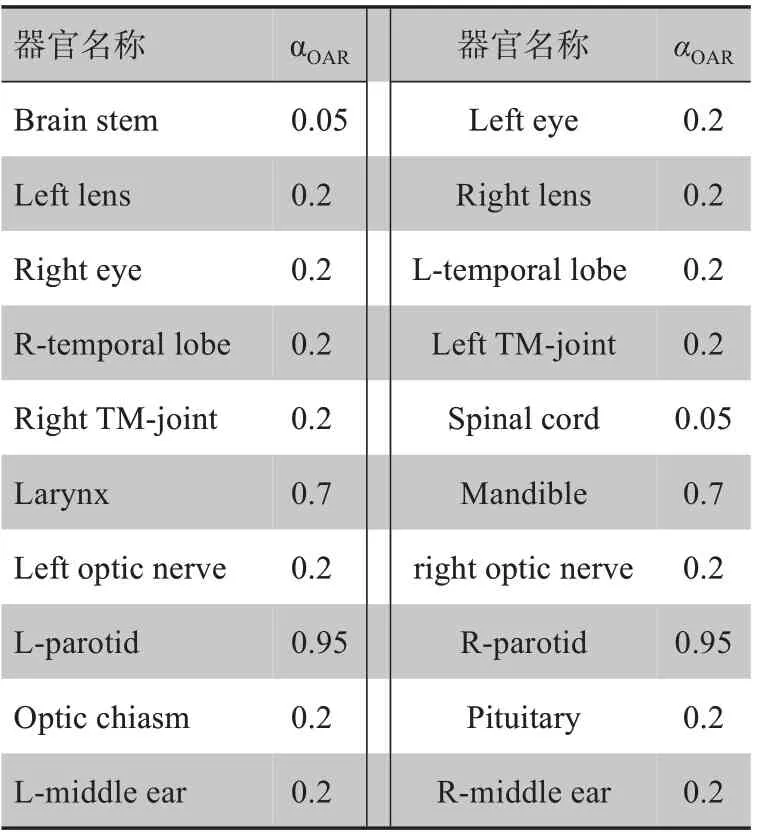
表1 系数因子αOAR的取值Tab.1 The value of coefficient factor αOAR
如直接将头颈部肿瘤中每个危及器官对应的目标函数fOAR看成目标函数,联合肿瘤靶区约束条件进行放疗计划优化,则优化目标有20多个,要生成多目标优化模型(2)中的Pareto 前沿几乎无法实现。因此,我们基于放疗计划的先验知识,回顾性地计算了71 位同类患者IMRT 计划中所有危及器官的线性EUD 函数值,再对所有危及器官按线性EUD 进行R型聚类分析[19],其基本步骤为:
首先,各危及器官单独为一类,对线性EUD剂量,计算危及器官两两之间的Pearson相关系数;其次,将相关系数最大的两类器官合并为一新类,同时剔除该器官所在的原始类;再次,计算新类与其他类之间的相关系数,重新生成新类,直至所有危及器官聚为一类为止。其中,类与类之间的相关系数利用类平均法进行计算,即对两类E1和E2,则两类之间的相关系数为:

其中,r(i,j)为危及器官i、j之间的相关系数,i、j分别属于类E1、E2。如考虑危及器官A1~A6 的R 型聚类分析,假设编号依次为1~6,危及器官之间的相关系数矩阵见表2。

表2 相关系数矩阵Tab.2 Correlation coefficient matrix
进行R型聚类分析时首先每个器官各成一类,即聚为6类的结果为{{1},{2},{3},{4},{5},{6}},根据器官之间的相关系数矩阵及类平均法的计算公式(5)可知,类{1},{2}之间的相关系数最大,为0.763,因而{1},{2}两类可合并为一个类{1,2}。所以R 型聚类分为5 类的结果为{{1,2},{3},{4},{5},{6}},计算其余各类与类{1,2}之间的相关系数。
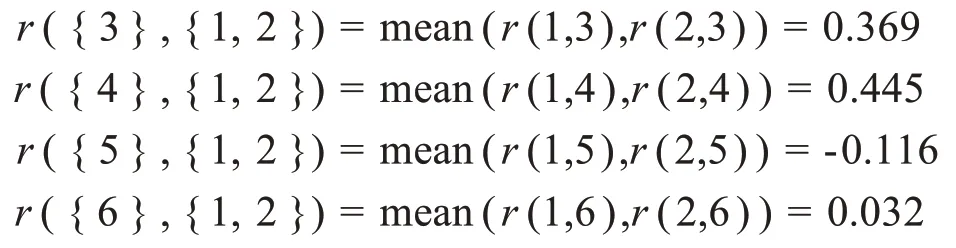

对比5类之间的相关系数,类{3},{4}之间的相关系数最大,为0.708。因此,进一步聚为4 类的结果为{{1,2},{3,4},{5},{6}},计算其余各类与类{3,4}之间的相关系数。对比4类之间的相关系数,类{1,2},{3,4}之间的相关系数最大,为0.407,因此,进一步聚为3 类的结果为{{1,2,3,4},{5},{6}}。依此类推,直至所有危及器官全部被合成一类为止,其聚类的树状图见图1。

图1 R型聚类分析的树状图Fig.1 Tree diagram of R-mode cluster analysis
对回顾性的71 例头颈部肿瘤患者,放疗计划设计过程中共考虑了18 个主要危及器官。按R 型聚类分析方法,其聚类的树状图见图2。

图2 危及器官的R型聚类分析树状图Fig.2 Dendrogram of R-mode clustering for organs-at-risk
从图2可知,如将所有危及器官分为3 类,则具体的分类为:
一类:Left eye,Left lens,Right lens,Right eye;二类:Spinal cord,Brain stem;三类:Pituitary,Left optic nerve,Right optic nerve,L-parotid,R-parotid,Mandible,Larynx,Left TM-joint,Right TM-joint Ltemporal lobe,R-temporal lobe,Optic chiasm。
对于每一类,我们将所有危及器官的线性EUD平均值看作多目标IMRT计划优化的目标函数,即
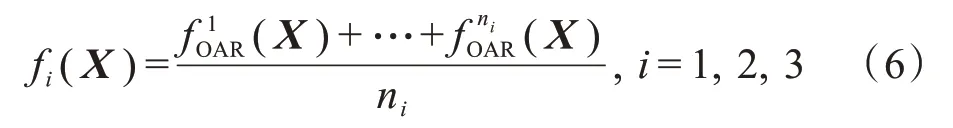
其中,ni表示各类中危及器官的个数。因此,在多目标IMRT 计划优化过程中,如对所有危及器官按类构造目标函数,则可将原多目标IMRT计划优化中的18个危及器官目标函数缩减为3个,极大程度减少了待优化的目标函数个数。
1.3 多目标优化的Pareto前沿近似方法
对放疗计划的多目标优化模型(2),如直接生成其对应的Pareto 前沿,需要更多的Pareto 最优解集,且大多解对应的放疗计划无临床意义,因此我们考虑对肿瘤靶区添加适当的先验约束,使生成的Pareto前沿仅包含临床有意义的部分。参考Craft等[20]前期的工作,对肿瘤靶区PTV,定义斜坡函gPTV如下:
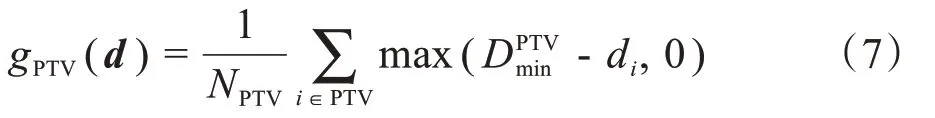
其中,NPTV表示靶区PTV 的体素总数,di为PTV 的第i个体素剂量值,并定义先验约束条件如下:

将上述先验约束条件(8)加入到模型(2)中,得多目标IMRT计划优化模型(9):

1.3.1 目标函数值范围界定为生成模型(9)中的Pareto 前沿,现有的夹心算法需要对各目标函数进行归一化,即将目标函数的取值范围归一化到[0,1]之内,因而需要事先确定模型中各目标函数的取值范围。目前,确定目标函数取值范围的方法是令各目标函数值分别最小,通过优化寻找到一组初始锚点,再根据各锚点的取值确定目标函数的取值范围[6]。该方法所确定的范围可能只是其实际取值范围的一部分,因而生成的Pareto 前沿可能不完整。如,考虑下面3个目标函数的优化问题。

其中,函数fi=xi,i=1,2,3,该多目标优化问题对应的Pareto前沿见图3。
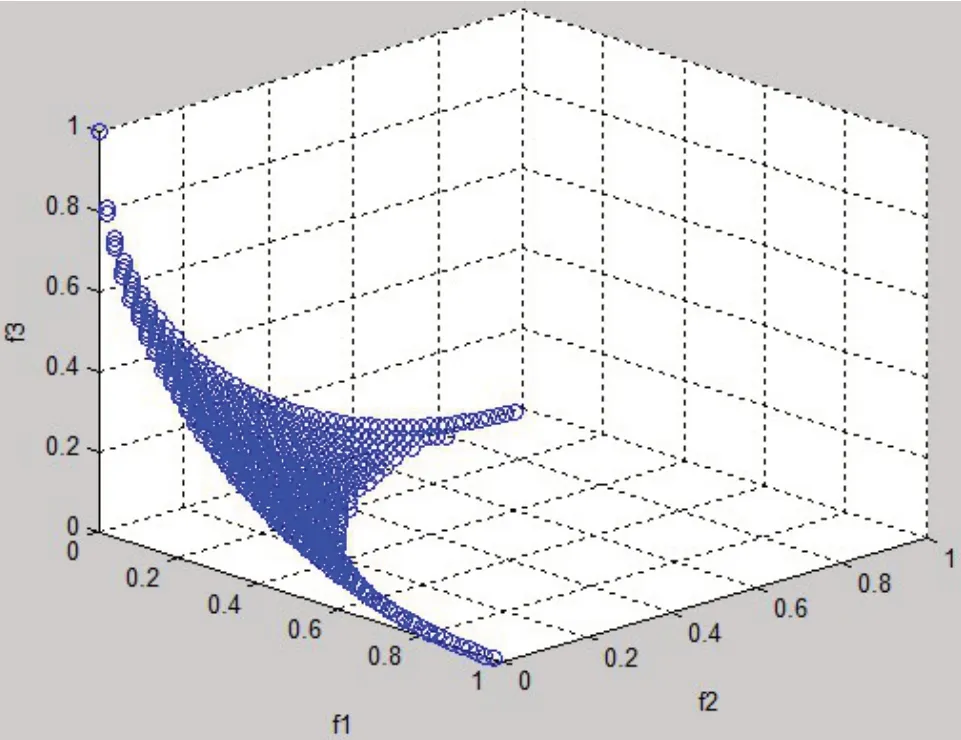
图3 多目标优化问题(10)的Pareto前沿Fig.3 Pareto frontier of multi-criteria optimization(10)
如通过令各目标函数f1、f2、f3分别最小来确定各目标函数的取值范围,可以得到3 个锚点,分别为(0,0.5,0.5)、(0.5,0,0.5)、(0.5,0.5,0)。由这3 个锚点所确定的目标函数取值范围仅为[0,0.5],并非目标函数的实际取值范围[0,1]。为尽可能生成完整的Pareto 前沿,本文利用Singh 等[21]在多目标函数值空间降维过程中提出的角解方法,确定各目标函数的取值范围,即在多目标优化模型中,依次令每个目标函数最小,同时,也让剩余n-1 个目标函数之和最小,得2n个Pareto 最优解,这些解称为角解。目标函数的取值范围由这2n个角解确定,如对上述3 个目标函数的多目标优化问题,分别令f1、f2、f3、f2+f3、f1+f3、f1+f2最小,求得6个角解,见表3。
根据表3可知,目标函数f1、f2、f3的取值范围都是[0,1],与实际取值范围一致。

表3 多目标优化的6个角解Tab.3 Six corner solutions of multi-criteria optimization
1.3.2 Pareto 前沿近似方法为求解模型(9),我们联合Rennen 等[6]提出的增强夹心算法与Singh 等[21]生成角解的方法,提出了逼近Pareto 前沿的新方法,即基于角解的增强夹心算法,该算法基本思路如下:
step1 生成初始锚点;
在模型(9)中,依次令每个目标函数最小,同时,也让剩余n-1 个目标函数之和最小,得模型(9)Pareto前沿上的2n个角解,即初始锚点:
zA1,…,zAn和zM1,…,zMn
step2 添加辅助点,生成凸壳,形成“上界面”;
设所有锚点组成的集合为Z,令ziub为Z 中第i个目标函数的最大值。为使锚点生成凸壳面时各面的法向量非负,对集合Z中的每个锚点z=(z1,...,zn)T,添加n个辅助点dj(z),j=1,2,…,n,如下:
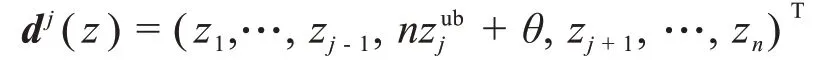
其中,θ>0是任意给定非常小的正数。
所有辅助点的集合记为E,锚点Z与辅助点E共同生成的凸壳为IPS,则该凸壳面形成了Pareto 前沿的一个“上界面”(图4)。
step3 生成“下界面”;
对集合Z 中每个锚点z,Pareto 前沿上存在过该点的切平面λTp=λTz,其中λ是该切平面的法向量,令
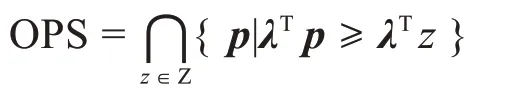
则OPS 的边界构成了Pareto 前沿的一个“下界面”(图4)。
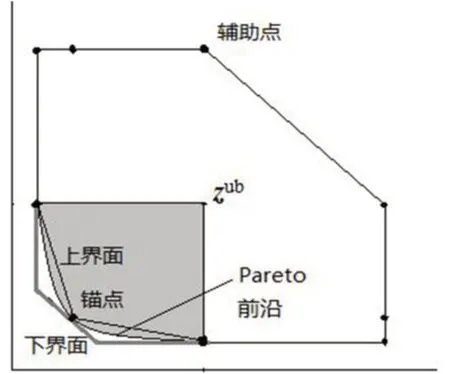
图4 基于角解的增强夹心算法示意图Fig.4 Schematic diagram of enhanced sandwich algorithm based on corner solutions
step4 确定“上、下界面”误差;
对凸壳面IPS,我们按照Solanki 等[22]的 算 法xnise2提取相应的超平面及法向量。
步1:在IPS 中找出有n个点属于Z的超平面;所有超平面的集合记作IPSnld,并在IPS中剔除相应的超平面;
步2:在IPS 中找出有n-1 个点属于Z的超平面,如这n-1 个点属于IPSnld中的某个超平面,则剔除这n-1个点所在的超平面;
步3:更新n,让n=n-1,如n≥1,返回步2,否则进入步4;
步4:修正IPSnld。在IPSnld中,如存在多个超平面,其属于Z中的锚点相同,则将这多个超平面合并成一个过这些相同锚点的超平面,其法向量取原多个超平面法向量的平均值;
步5:确定“上、下界面”误差。对IPSnld中的每个超平面,设其对应的方程为wTp=b,求解模型(11),得最优解:

计算该超平面到“下界面”之间的距离e:

其中,ε为参数向量,当无特别要求时常取ε的每个分量为对应目标函数取值区间的长度,特别当目标函数的取值范围为[0,1]时,此时ε的取值为ε=(1,1,…,1)T,如同时w的各分量之和等于1,则误差e=b-wT变为Solanki 等报道的夹心算法中的逼近误差。
“上、下界面”间的误差e*定义为IPSnld中所有超平面到“下界面”之间距离的最大值。
step5算法终止条件;
如“上、下界面”误差e*小于事先给定的阈值,则算法终止,输出所有锚点的集合Z。否则,从IPSnld中选取一个具有最大误差e*的超平面F*,设该面F*的方程为wT0p=b0,进入step6。
step6 生成新的锚点;
在模型(9)中,对各目标函数赋权,权重为超平面F*的法向量w0,将原多目标优化问题可转化为单一目标函数的最优化模型(13)。

求解模型(13),得F(d)的最优解为如z*在超平面F*上,令超平面F*到“下界面”的距离为0,更新“上、下界面”之间的误差e*,返回step5,否则进入step7。
step7 更新锚点集合
更新锚点的集合Z=Z∪{z*},返回step2。
根据step1~step7,基于角解的增强夹心算法的具体流程见图5。
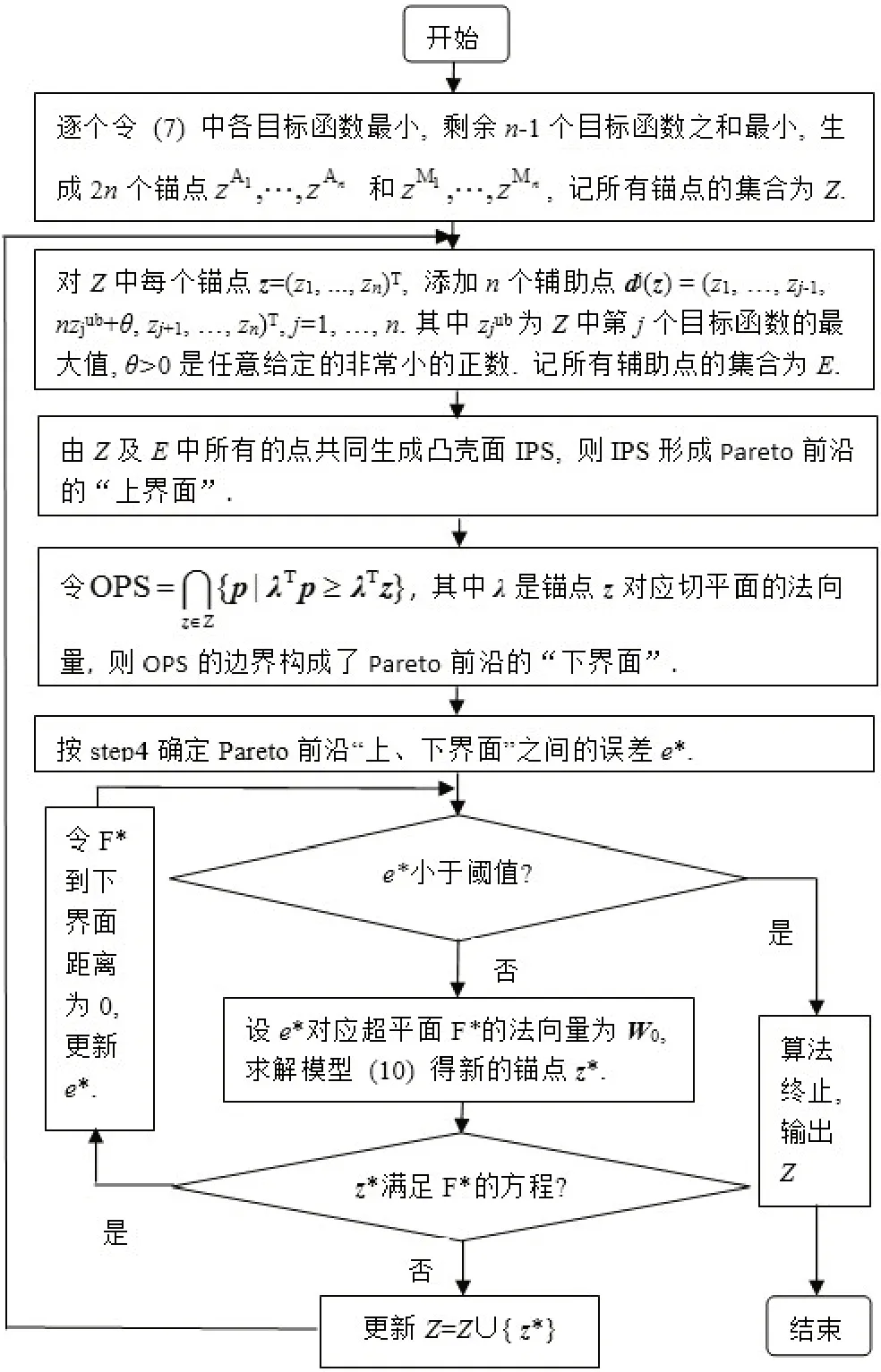
图5 Pareto前沿近似流程图Fig.5 Flow chart of Pareto frontier approximation
1.4 Pareto前沿导航
由上述基于角解的增强夹心算法,可以在Pareto前沿上寻找到一组锚点,这些点的凸壳构成了Pareto前沿的近似。设计者可以通过实时导航方法[9,23-24],并根据临床放疗剂量评估指标(剂量分布情况、剂量体积直方图等),可视化地从众多Pareto 最优IMRT计划中快速选出一个导航放疗计划作为临床最终的执行计划。本文利用Craft[25]的Pareto 前沿导航软件,联合放疗计划软件CERR[26]进行实时导航选取合适的放疗计划。
2 实验结果
2.1 鼻咽癌IMRT计划
本文回顾性选取71 例鼻咽癌患者,并从中选取两例患者进行对比实验验证分析。患者临床IMRT计划的PET/CT 影像和IMRT 计划数据均来源于湖南省肿瘤医院放疗中心。两例患者的放疗靶区与危及器官(脑干等)由临床放疗专家通过商用放疗计划系统Nucletron Oncentra MasterPlan v3.2 手动勾画完成。临床IMRT计划的射束角度为0o、51o、103o、155o、206o、257o、309o。
患者1 的放疗靶区包括GTVPET、CTV、PTV,所有靶区都考虑最大剂量、最小剂量约束,同时对靶区GTVPET考虑均匀剂量约束,具体约束条件见表4。放疗计划设计优化过程考虑的危及器官有17 个,按R型聚类分析结果,共分为3类:

表4 患者1的靶区剂量约束Tab.4 Target dose constraints for patient 1
1类(OAR1):Left eye,Left lens,Right lens,Right eye;
2类(OAR2):Spinal cord,Brain stem;
3类(OAR3):Optic chiasm,Left optic nerve,Right optic nerve,Mandible,Larynx,Left TM-joint,Right TM-joint,L-temporal lobe,R-temporal lobe,Lparotid,R-parotid
对这3类危及器官中的每一类,其对应的目标函数按式(6)构造,共3 个目标函数。对该患者,IMRT计划设计优化过程中考虑的靶区共有3个,对应的目标函数按式(3)构造,共3 个目标函数。因此,患者1的放疗计划优化问题,其实是6个目标的多目标优化问题。
患者2 的放疗靶区包括PET-GTVnx、PETGTVnx+1.0、UP of CTV、Down of CTV,所有靶区都考虑最大剂量、最小剂量约束,同时对靶区PETGTVnx考虑均匀剂量约束,具体约束条件见表5。放疗计划设计优化过程考虑的危及器官有17个。对比患者1,在第3 类危及器官中增加了Pituitary,但减少了危及器官larynx。患者2 的放疗计划优化问题,其实是7个目标的多目标优化问题。
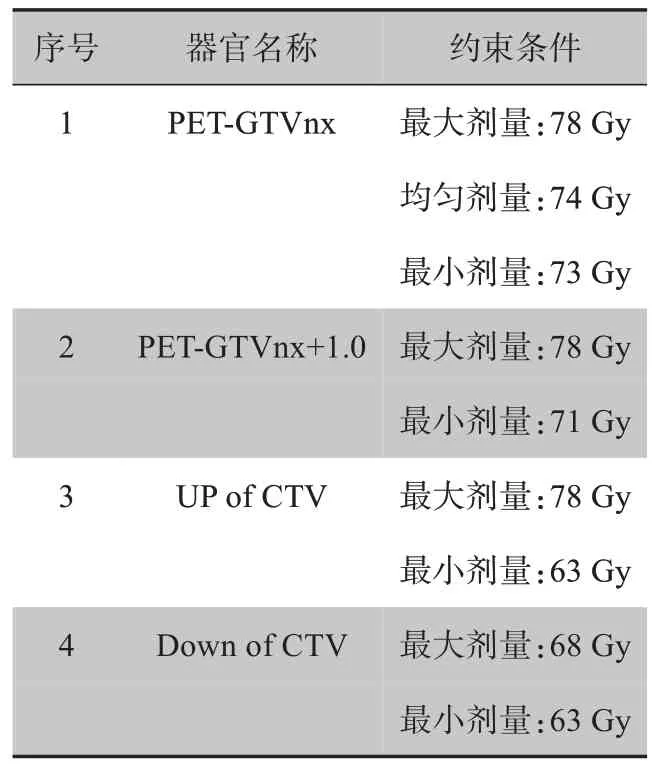
表5 患者2的靶区剂量约束Tab.5 Target dose constraints for patient 2
2.2 Pareto前沿逼近
对上述两例患者,采用基于角解的增强夹心算法逼近模型(9)中的Pareto 前沿。在逼近过程中,预设允许误差为5%。对患者1,优化过程中共生成了57 个锚点;对患者2,优化过程中共生成了116 个锚点。这些锚点的凸壳面构成了Pareto 前沿的一个逼近。由于这些都是6 或7 维的锚点,无法在笛卡尔直角坐标系中直观地显示,我们绘制出了其平行坐标图[27],即横坐标代表锚点的各个分量,纵坐标代表各分量的取值,平行坐标图中的每根折线代表一个锚点,见图6和图7。可以看出对每个目标函数的取值,都存在一定的取值区间,因而可以进行放疗计划的导航并进行可视化的放疗计划评估。

图6 患者1所有锚点的平行坐标Fig.6 Parallel coordinates of all anchor points for patient 1
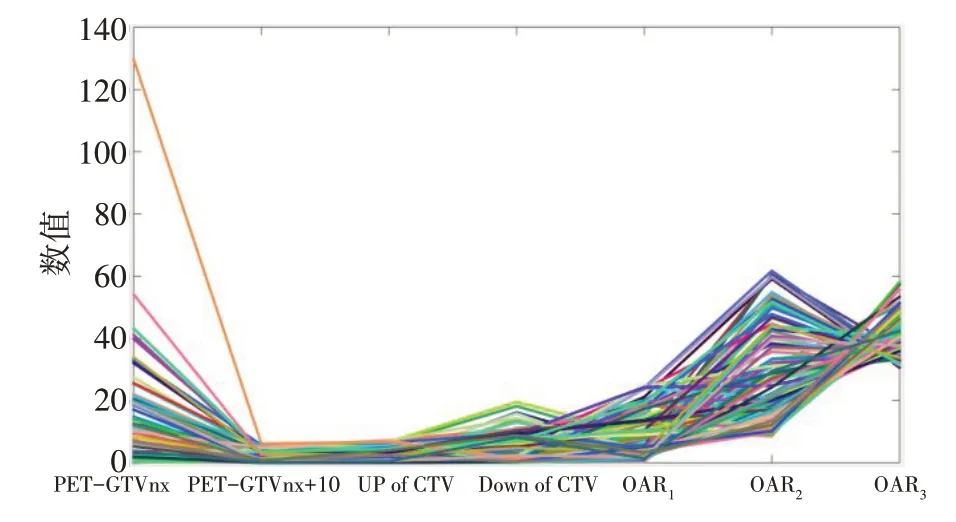
图7 患者2所有锚点的平行坐标Fig.7 Parallel coordinates of all anchor points for patient 2
2.3 放疗计划导航与评估
对已有的Pareto 前沿近似曲面,使用Craft 等的Pareto 前沿导航软件,联合放疗计划软件CERR 进行验证评估,可在Pareto前沿的近似曲面上快速选择一个导航计划。图8显示患者1 的6 个目标导航界面。中间的可滑动选择控件对应上述6 个目标函数的取值,中间的可滑动小方块可以上下移动,向上移动表明该目标函数值变大,反之表明缩小目标函数的取值。图中所有小方块所在位置对应一个导航放疗计划,其剂量分布如图9所示。

图8 导航界面(从左至右,依次为GTVPET、CTV、PTV、OAR1、OAR2、OAR3对应的目标函数)Fig.8 Navigation interface(from left to right,the criteria corresponding to GTVPET,CTV,PTV,OAR1,OAR2,OAR3,respectively)
为验证该方法的有效性,本文将选取的导航计划与临床计划分别从剂量分布、剂量体积直方图、靶区剂量分布的定量指标、危及器官剂量分布的定量指标4个方面进行对比分析,具体方法如下。
2.3.1 剂量分布对比对比患者1 临床计划的剂量分布图10,导航计划(图9)与临床计划有着近似的剂量分布,剂量都呈现由靶区向外围逐渐递减,导航计划的最大剂量为82.5 Gy,比临床计划的76.3 Gy 稍高。靶区GTVPET的剂量分布均匀在处方剂量68 Gy附近,图中"+"显示了GTVPET(中心紫色线)内部同一个位置导航计划与临床计划的剂量值,分别为68.75 Gy和71.67 Gy,在该处导航计划的剂量更接近GTVPET的处方剂量68 Gy。
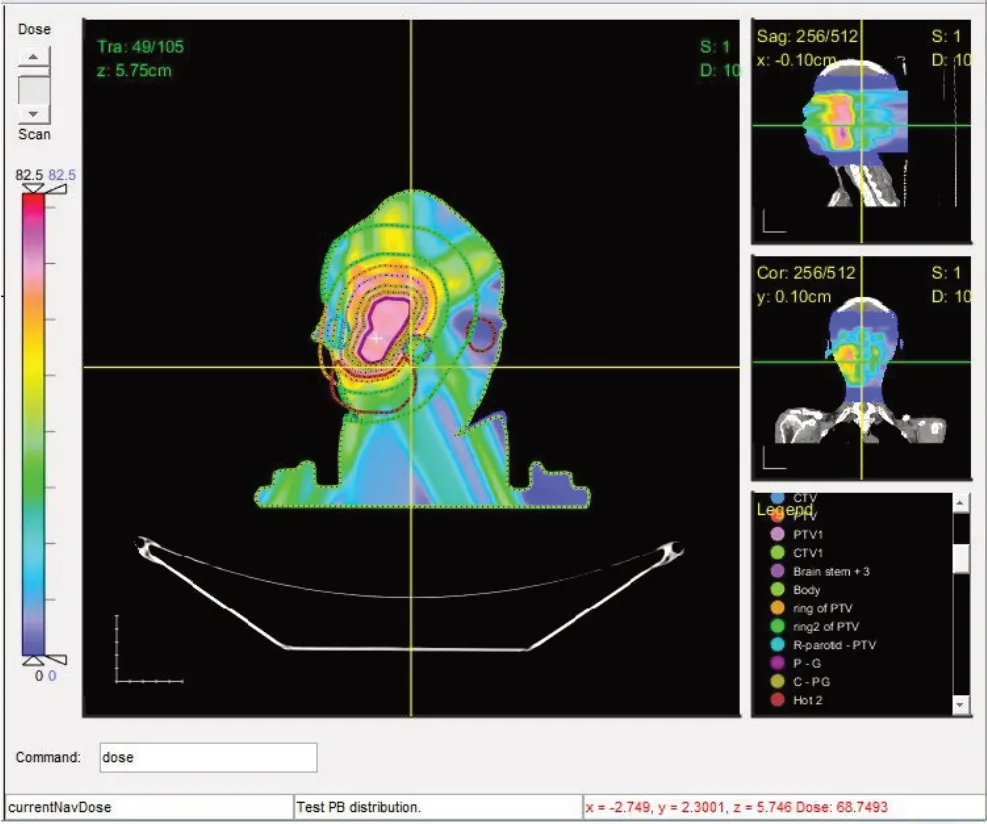
图9 导航计划对应的剂量分布Fig.9 Dose distribution of navigation plan
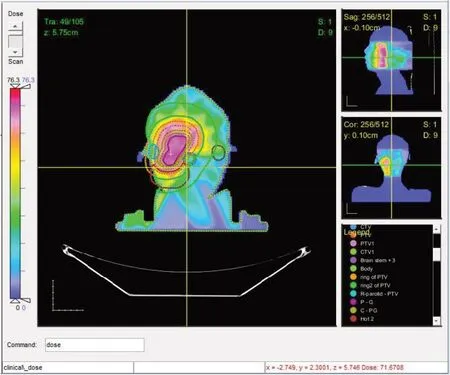
图10 临床计划对应的剂量分布Fig.10 Dose distribution of the clinical plan
2.3.2 剂量体积直方图对比为进一步评估靶区与各危及器官的剂量分布情况,我们绘制出两例患者导航计划与临床计划的靶区和危及器官DVH 图。图11是患者1各个靶区剂量的DVH 图。从该图可以看出导航计划与临床计划有着相似的剂量分布,且对靶区GTVPET,导航计划有更均匀的剂量分布。图12~14是患者1 的3 类危及器官剂量分布DVH 图。对第1类危及器官,除左晶体(Left lens)外,其它危及器官的剂量分布导航计划都要优于临床计划(图12);对第2 类危及器官,脊髓(Spinal cord)的剂量分布两种计划剂量分布相当,但对脑干(Brain stem)的剂量分布,临床计划的结果更好(图13);对第3类危及器官,绝大多数危及器官的剂量分布在导航计划下要比临床计划更优(图14)。

图11 靶区的DVH图Fig.11 Dose-volume histogram of target areas

图12 第1类危及器官剂量分布的DVH图Fig.12 Dose-volume histogram of organs-at-risk of the first category

图13 第2类危及器官剂量分布的DVH图Fig.13 Dose-volume histogram of organs-at-risk of the second category
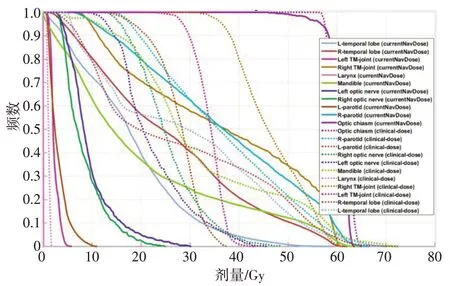
图14 第3类危及器官剂量分布的DVH图Fig.14 Dose-volume histogram of organs-at-risk of the third category
患者2 进一步验证了导航计划能生成与临床相当且对部分危及器官保护更好的放疗计划。图15是患者2 的一个导航计划中各个靶区剂量分布的DVH图。对靶区UP of CTV 和Down of CTV,导航计划将剂量的平均值由临床计划的69.10和65.27 Gy提升到了71.02 和66.36 Gy;对靶区PET-GTVnx,虽然导航计划的剂量平均值只有74.04 Gy,相对临床计划的剂量平均值(75.67 Gy)较低,但导航计划的剂量分布更均匀,且更接近处方剂量74 Gy。图16是同一导航计划主要危及器官的DVH 图。对大多数的危及器官,导航计划的剂量分布要优于临床计划,但少数危及器官例外,如对危及器官L-parotid、R-parotid,导航计划的最大剂量要比临床计划大。

图15 患者2靶区的DVH图Fig.15 Dose-volume histogram of target areas in patient 2

图16 导航计划部分危及器官剂量分布的DVH图Fig.16 Dose-volume histogram of some organs-at-risk in navigation plan
2.3.3 靶区均匀性指数与适形度指数对比为进一步定量评估靶区剂量的分布情况,我们按下面公式分别计算出两例患者的各个靶区在导航计划和临床计划下的均匀性指数(HI)[28]和适形度指数(CI)[29]。

其中,D5和D95表示靶区5%与95%体积所得到的绝对照射剂量,Dp为靶区的处方剂量,TVRI表示被等剂量面包绕的靶区体积,TV 为靶区的体积。HI 反应靶区的剂量分布均匀程度,值越小越好,而CI指数的值越大,说明被等剂量面包绕的靶区体积越大。
实验中两例患者HI和CI的计算结果见表6和表7。对患者1 的所有靶区,导航计划的HI 指数值更小,因而靶区剂量分布具有更好的均匀性,但对靶区GTVPET,导航计划下的CI 指数稍低(表6)。对患者2的靶区UP of CTV、Down of CTV,导航计划具有更好的CI;对靶区PET-GTVnx,导航计划的HI 指数值更小,因而对该靶区导航计划下的剂量分布具有更好的均匀性,但对其它评价指标,导航计划要比临床计划差(表7)。也许通过适当更换导航计划,可以进一步消除这种现象。

表6 患者1靶区定量评估指标HI与CITab.6 Quantitative evaluation indexes HI and CI of target areas in patient 1

表7 患者2靶区定量评估指标HI与CITab.7 Quantitative evaluation indexes HI and CI of target areas in patient 2
2.3.4 危及器官的并发症对比为进一步定量评估危及器官的剂量分布情况,我们根据Lyman-Kutcher-Burman(LKB)模型[30-31]计算出部分主要危及器官的并发症(NTCP):
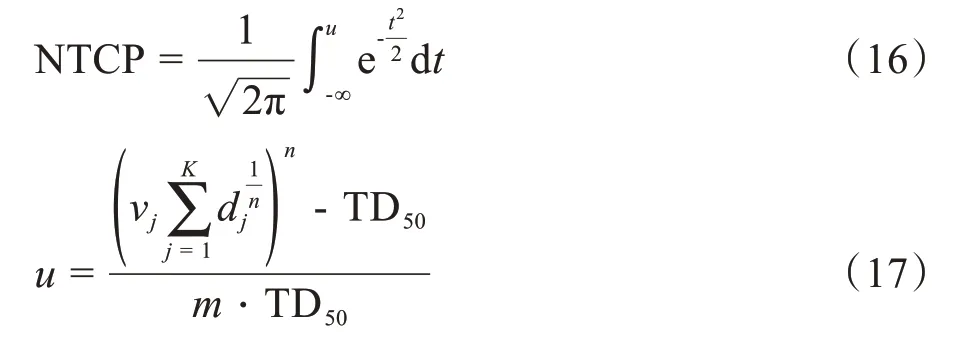
其中,式中vj表示危及器官的第j个体素占总器官的体积比,K表示危及器官的体素总个数,dj为第j个体素受照剂量,n、m、TD50为参数,具体取值见表8。对实验中考虑的所有危及器官,表9列出了其中13 个主要危及器官导航计划与临床计划的NTCP 结果。从表9的NTCP 结果可以看出,导航计划对大多数危及器官的保护要好于临床计划,如实验中的右腮腺(R-parotid),对比临床计划,两例患者的NTCP 都有不同程度的减少,患者1 的NTCP 值由原来的0.12 减少到0.11,减少了8.3%;患者2 的NTCP 值由原来的0.084 减少到0.032,减少了61.9%。但也有个别危及器官的NTCP增大,如患者2中的左腮腺(L-parotid),NTCP的值从临床计划的0.07增加到0.13。
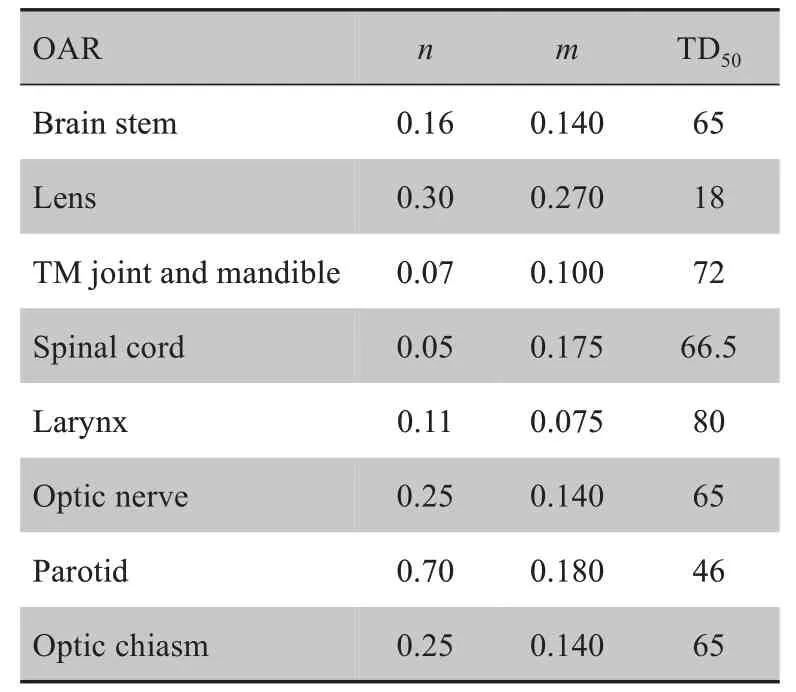
表8 NTCP中参数n,m,TD50的取值Tab.8 Values of parameters n,m and TD50 in NTCP

表9 主要危及器官的NTCPTab.9 NTCP of primary organs-at-risk
3 讨论
本文回顾性对71 例头颈部肿瘤患者按R 型聚类分析方法,将放疗计划设计过程中的18 个主要危及器官聚为3类,因而能极大程度地降低优化目标函数的个数,但具体聚为多少类合适仍需进一步探索。虽然,有众多的评价指标帮助我们从聚类的树状图中选择最佳的聚类个数,但最佳聚类个数与评价指标的选取有极大关系,甚至对类别个数已知的聚类问题,不同的评价指标会得到完全不一样的聚类个数[32]。为能有效逼近Pareto前沿,最终的聚类个数选取不能太大,否则进行多目标IMRT 计划优化时对应的Pareto 前沿维度会非常高,无法生成其近似曲面。因此,我们选择Dunny 指标作为评价指数,对图2中聚类结果的树状图分别计算了聚为2、3、4、5 类的Dunny 指标结果[33-34],按指标值越大越好的原则,选取将所有危及器官聚为3类作为最佳的聚类个数。
为便于计算各危及器官的线性EUD 剂量,我们选取了适当的系数因子α。虽然α的确定与危及器官是串行或并行相关,但缺少大量的实验数据及相关资料佐证,如α 取值为1,则危及器官的线性EUD 变为该器官剂量的平均值;如α的取值为0,则危及器官的线性EUD 变为最大剂量值。因此,当α 取值介于0和1 之间时,危及器官的线性EUD 介于其最大剂量和平均剂量之间。为进一步探索系数因子α 对优化结果的影响,对实验患者中的第1 例,我们将表1中系数因子α 的取值做适当修改,即系数因子小于0.5的取为0.05,大于0.5 的取为0.95,在模型(13)中让各目标函数的权重相等并求出不同系数因子下的两个放疗计划。对比系数因子按表1取值的计划(plan1),修改系数因子α 后的计划(plan2)对优化结果的影响并不大。修改系数因子的主要差别,体现在是约束危及器官剂量的最大值还是危及器官剂量的平均值上。例如,对危及器官Right TM-joint,将系数因子由表1中的0.2 修正为0.05 后,该危及器官剂量的最大值由计划plan1 中的61.9 Gy 降低到计划plan2 中的60.7 Gy,但对该危及器官,系数因子取0.2 比0.05 可能更合理,因为系数因子的这两个取值,目标函数同样都是侧重考虑最大剂量约束,但前者更大程度地考虑了该危及器官平均剂量的约束。因此,计划plan1 中的剂量平均值明显要低于计划plan2,分别为35.76 和42.37 Gy。类似的情形在危及器官Mandible中再次出现,系数因子取0.7 比0.95 在适当增大危及器官Mandible的平均剂量情况下(22.65和21.27 Gy),可使该危及器官的最大剂量值由plan1 中的71.3 Gy降低到计划plan2中的67.1 Gy。
4 总结
将头颈部肿瘤临床IMRT 计划先验知识集成到放疗计划多目标优化模型中,通过对各危及器官按线性EUD 进行R 型聚类分析,可将头颈部肿瘤IMRT计划的多目标优化模型中的20~21 个目标函数减少到6~7 个目标函数,因而极大程度简化了其Pareto 前沿。同时,为进一步有效逼近其Pareto 前沿,在增强夹心算法的基础上,我们提出了基于角解的增强夹心算法,使生成的Pareto 前沿近似曲面更完整。在Pareto 前沿的近似曲面上,借助可视化导航,放疗计划设计者可以快速地确定一个导航计划,并能实时观察该导航计划的剂量分布、DVH 图等剂量信息。对比临床计划,实验结果表明该方法能生成与临床IMRT 计划质量相当、部分指标更优的放疗计划,且能根据需要实时调节靶区与各危及器官的剂量分布。但本文在优化过程中对肿瘤靶区仅考虑将均匀剂量、最大及最小剂量作为约束条件,并未考虑靶区的体积约束情形,因此剂量体积约束的多目标优化问题是我们进一步需要研究的内容之一。
——《艺术史导论》评介

