Block-Gebhart模型分区数对预测大空间热环境参数及负荷的影响*

上海理工大学 路凯文 黄 晨同济大学 李瑞彬同济大学建筑设计研究院(集团)有限公司 刘 洋上海理工大学 王 昕 王海东 王 非

0 引言

大空间分层空调与全室空调相比，能耗更低[1-3]；与小空间建筑相比，大空间空调负荷与其热环境更加密切相关。准确计算夏季分层空调建筑的室内热环境参数对评估与优化室内热环境、准确预测分层空调负荷具有非常重要的意义。分层空调气流组织形式中，侧墙下送风、中部回风是一种新型的置换式气流组织，它具有较好的节能潜力[4]，其室内热环境参数的计算方法值得关注。

大空间建筑具有竖向温度分层的特点[5-7]。很多学者采用CFD模拟、统计学模型、Block模型、Block-Gebhart模型(下文简称B-G模型)等对热环境进行预测。CFD模型可以得到计算范围内的详细流场数据，但是通常需要针对目标建筑建立详细的物理模型，物理模型不同，可能导致结果不同。由于大空间竖直方向温度分层显著，而水平方向热环境比较均匀，有学者利用此特点在竖直方向上采用节点模型解析。Li等人通过建立竖直方向各节点所在区域内的热平衡方程，计算了竖向温度分布[8]。Wang等人假定高大空间室内空气在竖直方向上的温度分布遵循贝塔分布的累积分布函数，采用统计学分布研究了竖直方向上的温度分布，认为可以用4个点或2个点的温度来预测竖直方向上的温度分布[9]。Togari等人提出了Block模型[10]，属于Zonal模型[11-12]，建立了基于质量平衡和能量平衡的方程，将室内区域划分为水平方向的主流区和边界区，将竖直方向划分为若干个区域并假设每个区域温度是均匀的。Block模型在近壁面边界区建立壁面流模型，通过给定壁面温度，求解能量平衡方程以得到室内竖向各区域空气温度。黄晨等人完善了Block模型[13-15]。Gebhart提出的Gebhart辐射模型可以用较简单的数学形式来计算壁面间直接辐射和一次反射辐射的辐射传热量，且具有较高的准确性[16]。蔡宁将可以计算室内空气温度的Block模型和可以计算墙体内表面温度的Gebhart模型结合起来成为B-G模型，来预测室内热环境[17]。Liu等人基于缩尺模型建立了下部送风分层空调的B-G模型，计算了不同热源、排风量下的热环境参数，实验结果表明，B-G模型能够较好地预测室内热环境参数及分层空调负荷[18]。

高大空间建筑的负荷计算在实际工程应用中十分重要。Xu等人针对采用地板送风、中部回风、顶部排风的大空间分层空调系统，提出了一种通过CFD求冷负荷因子并用于计算空调区冷负荷的方法[19]。邹月琴等人提出了采用喷嘴送风系统的大空间分层空调负荷计算方法，该方法的核心是在空调区传统空调负荷(如建筑围护结构负荷、室内热负荷及新风或渗透风造成的冷负荷等)的基础上加上来自于非空调区的辐射和对流热转移负荷，并基于实验数据给出了适用于喷嘴送风系统的计算图表[20-21]。张倩茹针对下送风、中部回风、顶部无排风的分层空调系统，提出了基于B-G模型的对流热转移冷负荷计算方法[22]。Huang等人采用B-G模型预测了室内热环境参数并计算了分层空调负荷，分析了B-G模型预测室内热环境参数及分层空调负荷的影响因素[23-24]。

Gao等人基于喷口送风的分层空调系统建立了Block模型与直接辐射模型，尝试将竖向空间划分为10～34个分区，理论研究了不同竖向分区数对Block模型求解竖向空气温度分布的影响，其研究结果显示，不同分区数在预测竖向空气温度分布时有轻微不同[25]。因此，对于采用Block模型计算室内热环境参数时，分区数对结果的影响值得采用实验方法予以考证。

本文针对某下送风分层空调房间建立了2分区(2-Block)、4分区(4-Block)、7分区(7-Block)的B-G模型，实验验证了3种分区的B-G模型对室内热环境参数和分层空调冷负荷预测的准确性，并分析了不同分区数B-G模型计算结果间存在偏差的原因，为工程实践中应用B-G模型时分区数的确定提供参考。

1 计算模型

1.1 B-G模型

B-G模型将研究对象在竖直方向上划分为N个区域(下称N-Block模型)，N可取2到无限大。若每个Block对应的四面墙壁受到外界的热量影响一致，则可将每个Block对应高度的墙体看成一体，建立各区域质量和能量平衡方程组，其中空气能量平衡方程N个，壁面能量平衡方程N+2个。用迭代法求解方程组以预测室内热环境[24]。

由B-G模型可以得到以各分区空气温度和壁面温度为自变量的能量平衡方程组，其矩阵形式如下：

(1)

式中Aij为主流区空气热平衡方程中的空气温度系数，W/K，i表示第i层分区的热平衡方程的序号(从下向上递增)，j表示第j层分区空气温度的序号(从下向上递增)；Bil为主流区空气热平衡方程中的壁面温度系数，W/K，l表示第l层分区壁面温度的序号(从下向上递增)，l=f表示地面，l=c表示屋顶；αN为第N层内壁面的对流换热系数，W/(m2·K)；αf、αc分别为地面和屋顶内表面的对流换热系数，W/(m2·K)；Cil为壁面热平衡方程的壁面温度系数，W/(m2·K)；tj为第j层分区的空气温度，℃；θl为第l层分区的壁面温度，℃；Di为第i层分区热平衡方程中送风带入房间的热量与内热源对流散热量之和的负值，W；El为第l层分区壁面上来自墙体内部与内热源辐射散热热流密度之和的负值，W/m2。

1.2 分层空调负荷计算模型

Huang等人提出由上述B-G模型计算获得室内热环境参数并预测室内辐射热转移负荷及对流热转移负荷[24]，此时分层空调热负荷Q的计算式为

Q=Qkc+Qd+Qf

(2)

式中Qkc为空调区常规负荷，包括围护结构得热和内热源得热形成的负荷，W；Qd为对流热转移负荷，即非空调区向空调区转移的对流热量形成的负荷，W；Qf为辐射热转移负荷，即非空调区向空调区通过热辐射转移的热量形成的负荷，W。

1.3 N-Block模型的系数表达式

在已有B-G模型研究[17]的基础上，推导得到矩阵方程(1)中系数Aij和Bil在N等于任意值即任意分区数时的表达式，见表1。

表1 任意分区数时B-G模型各系数通式

因该模型较复杂，本文在此处给出的是能量平衡方程组的通式。表1中各量的具体确定方法见文献[15]。

表1中：

MC(i)=MIN(i)-MOUT(i)+MC(i+1)+

MS(i)-MR(i)-ME(i) (i=N时，

MC(i+1)=0)

(3)

(4)

(5)

(6)

(7)

本文分别建立了2分区、4分区、7分区模型来预测室内竖向温度分布，在此基础上，采用式(2)计算分层空调负荷。

2 模型验证及误差

2.1 实验概况

以某高大空间缩尺模型[24]为研究对象，该模型与实际建筑以约1∶4的比例建设，本文利用文献[24]的实验数据(包含不同高度的空气干球温度、内壁面温度、壁面热流密度、送风温度、送风速度、回风温度等)验证不同分区数B-G模型计算获得的室内竖向温度和分层空调负荷，进而计算得出分层空调系统的供冷量。

图1为缩尺模型实验室示意图，缩尺模型实验室长4.9 m、宽3.5 m，1.5～2.2 m高度为坡屋顶。沿实验室两面长边墙布置下送风口，每面墙等距布置3个，风口为半圆柱形，直径0.16 m，高0.313 m。回风口在每个送风口的上方，高度为1.1 m，为直径0.1 m的圆形风口。3条温度测线被布置在空间中(其中1条测线在水平中央，其余2条测线在其他水平位置)，3条测线上测点数分别为21、10、10个。针对实验对象，所建立的2、4、7分区模型如图2所示。在实验室墙壁和屋顶处敷设电热膜以模拟进入房间的墙体得热。具体工况见表2。

图1 缩尺模型实验室示意图

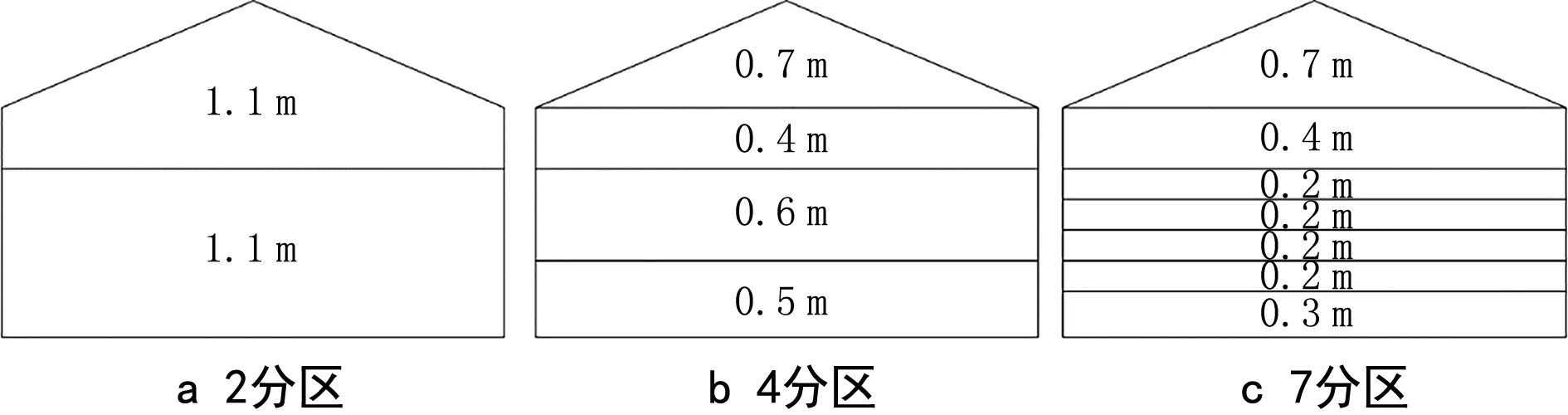
图2 分区示意图

2.2 误差指标

为了定量评估理论计算模型预测值与实验测量的温度、负荷之间的误差，定义如下参数：平均绝对相对误差(AARE)、均方根误差(RMSE)。

表2 研究工况汇总[24]

理论计算值与实验测量值之间的相对误差ηi的计算公式为

(8)

式中Yth,i为温度或负荷的理论计算值；Yex,i为温度或负荷的实验测量值。

某个工况所有预测点的AARE的计算公式为

(9)

式中n为预测点的个数。

RMSE的计算公式为

(10)

3 结果与讨论

3.1 室内热环境验证

通过模型理论计算得到的室内竖向空气温度分布与实验数据的对比如图3、4所示。由图3、4可以看出：2-Block、4-Block和7-Block模型预测的热环境温度分布理论值趋势一致，但存在一定偏移；4-Block、7-Block模型理论值与实验值较接近，而2-Block模型理论值与实验值差距较大。

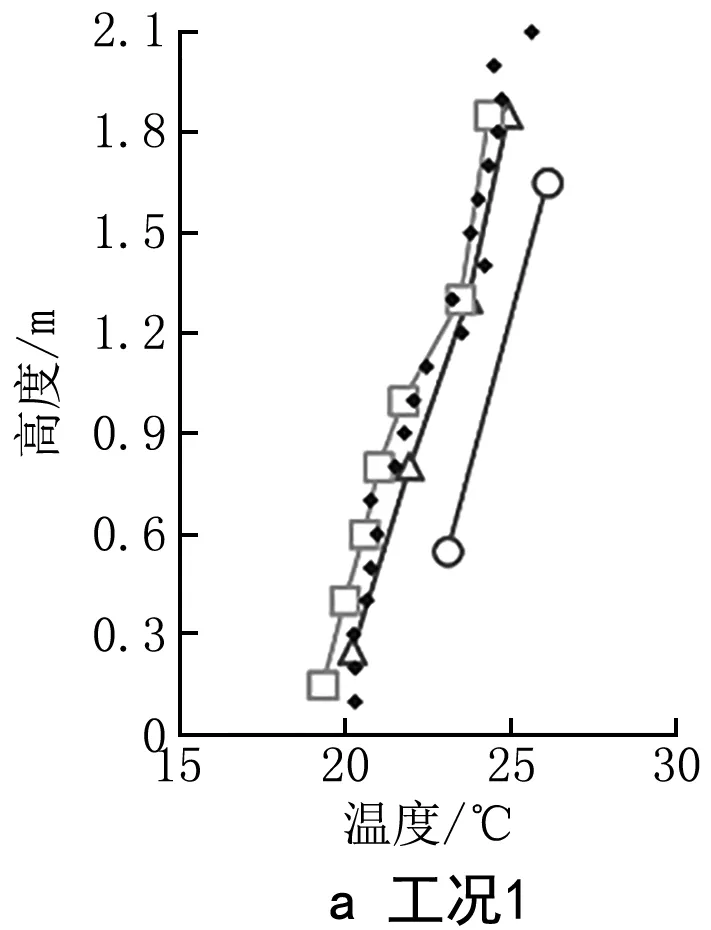
图3 不同工况下空气温度实验值与理论值的比较

图4 不同工况下壁面温度实验值与理论值的比较

7个工况的AARE和RMSE分别见表3、4。从表3、4可以看出，3种模型中4-Block模型空气温度和壁面温度的AARE和RMSE均最小，7-Block模型相对误差次之，而2-Block模型的相对误差最大。

误差的原因是模型采用了很多假定，如假定各区域内的温度均匀、有规则的壁面流、一维的温度分布等，这些都可能引起不同区域数计算结果的偏差；此外，模型区域数是否反映了研究对象的特征，对偏差也有很重要的影响。就本文所研究的对象而言，4-Block模型能较好地反映研究对象的建筑结构和送回风特点；2-Block模型将送风口和回风口放在了一个区域内，不能较好地体现送回风对环境的影响。与实验结果的对比分析可知，送回风口布置位置对于气流流动方向影响很大，区域划分应能充分反映建筑结构特点和室内气流组织。

表3 空气及壁面温度的AARE %

表4 空气及壁面温度的RMSE ℃

3.2 分层空调负荷理论计算值与实验值的对比

不同分区数下空调区冷负荷的理论计算值与实验值的对比及相对误差分别见图5和表5。由图5和表5可以看出：各个工况的4-Block模型计算值与实验值的误差都较2-Block、7-Block模型小；2-Block、4-Block、7-Block模型7个工况的计算值与实测值的相对误差分别小于18%、7%、28%；对于4-Block模型，7个工况的平均绝对相对误差为3.38%。该结果显示，采用4-Block模型计算室内下送风分层空调冷负荷较为准确，且适用于不同内热源、排风量、内热源高度工况。

图5 不同分区数下空调区冷负荷理论计算值与实验值的对比

4 结论

1) 建立了2-Block、4-Block、7-Block的B-G模型，计算了3个模型在不同工况下的室内温度分布和相应的分层空调负荷。

2) 不同工况下4-Block模型在计算室内热环境参数时准确性均较好，7-Block模型次之，2-Block模型误差最大。

3) 在计算不同工况的分层空调负荷时，4-Block准确性较好，但2-Block、7-Block模型出现了较大的误差。

表5 不同分区数下空调区冷负荷理论计算值与实验值的相对误差 %

4) 基于本文研究对象，分析计算结果表明，能较好地反映建筑结构、气流组织等特点是确定区域划分数的关键，过多的分区数不一定能增加其计算精度。