横向磁场作用下Taylor-Couette流动数值模拟

董 帅， 纪祥勇， 吕二飞， 李春曦

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

0 引 言

Taylor-Couette流动是流体力学经典问题，内圆筒旋转，外圆筒静止。随着内圆筒转速增加，流体在内外圆筒中间区域会呈现一系列流动形态，包括层流Couette流动、层流Taylor-Couette流动、波状Taylor- Couette流动、螺旋波状Taylor-Couette流动和湍流Taylor-Couette流动等[1]。将导电液体填充到内外圆筒中间区域，并置于外部磁场作用下，此时出现了一个新型的流动—磁流体Taylor-Couette流动。

通过磁场控制流体的运动被广泛应用到工业生产中，例如在材料制造领域，利用磁场控制熔融体的流动，可以有效提高晶体的生长质量[2, 3]。此外，磁流体技术还被应用到流量测量[4]、MHD发电[5]和金属冶炼[6, 7]等行业。泰勒涡反应器由于泰勒涡的存在，其独特的流动特性对混合、传热以及化学反应等有明显的提升效果，例如强化淀粉的糊化过程[8]，增强光催化反应器的效率，对污水进行有效处理[9]，以及提高环隙式离心萃取机的萃取效率[10]。在实际生产中，很多工质具有导电特性。导电液体Taylor- Couette流动在外加磁场的作用下，可以通过改变泰勒涡的结构，进一步控制泰勒涡反应器内部的反应过程，因此在工业生产中具有良好的应用前景。

磁场作用下，导电液体的流动控制问题引起了广大学者的研究兴趣。董帅等人对导电液体在磁场作用下的流动稳定性研究进行了深入发掘。对正则模态和非正则模态两种计算方法的进行了对比，阐述了管道形状、磁场方向、壁面电导率等因素对流动稳定性的影响[11]。董帅等人对平行平板内导电液体在法向磁场作用下的稳定性进行了研究。结果表明，初级扰动在平板导电和平板绝缘两种边界条件下的形成过程基本相同。在平板导电边界条件下，磁场对扰动的抑制效果更好[12]。Medebber等人对磁场作用下，液态金属Taylor-Couette流动进行了数值模拟，结果表明轴向磁场可以抑制二次流的形成，而环向磁场没有类似的阻尼效应[13]。冷学远等人采用数值计算方法，研究周期性边界条件下，轴向磁场对湍流Taylor-Couette流动的影响，分析了泰勒涡的演化过程，发现径向感应电流是导致湍流结构改变的主要因素[14]。Mahfoud等人对上下壁面反向旋转边界条件下，垂直环形间隙内导电液体的流动进行了数值模拟。研究发现，随着间隙尺寸的增大，液体呈现出不同的流动形态。在磁场作用下，流动从轴对称变为非轴对称[15]。

针对横向磁场作用下Taylor-Couette流动的研究较少。本文使用Fluent数值模拟软件，建立有限长和无限长两种模型。对Re=10和Re=259 两种工况，在不同磁场强度下的流动演化过程进行数值模拟，并对不同模型条件下的结果进行对比。

1 理论模型

1.1 物理模型

不可压缩流体在环形间隙内的流动模型，如图1所示。环形间隙由两个同心圆柱组成，半径比η=Ri/Ro=0.5，长宽比Γ=H/d=2。内圆筒以角速度ω进行旋转，外圆筒静止，壁面均为无滑移和电绝缘边界条件。计算所用模型分为有限长模型和无限长模型，上下壁面分别对应静止壁面边界条件和周期性边界条件。环形间隙内的流体为液镓，受到均匀横向磁场的作用。液镓的磁雷诺数远远小于1，即Rem《1，相比外部磁场，感生磁场忽略不计[16]。

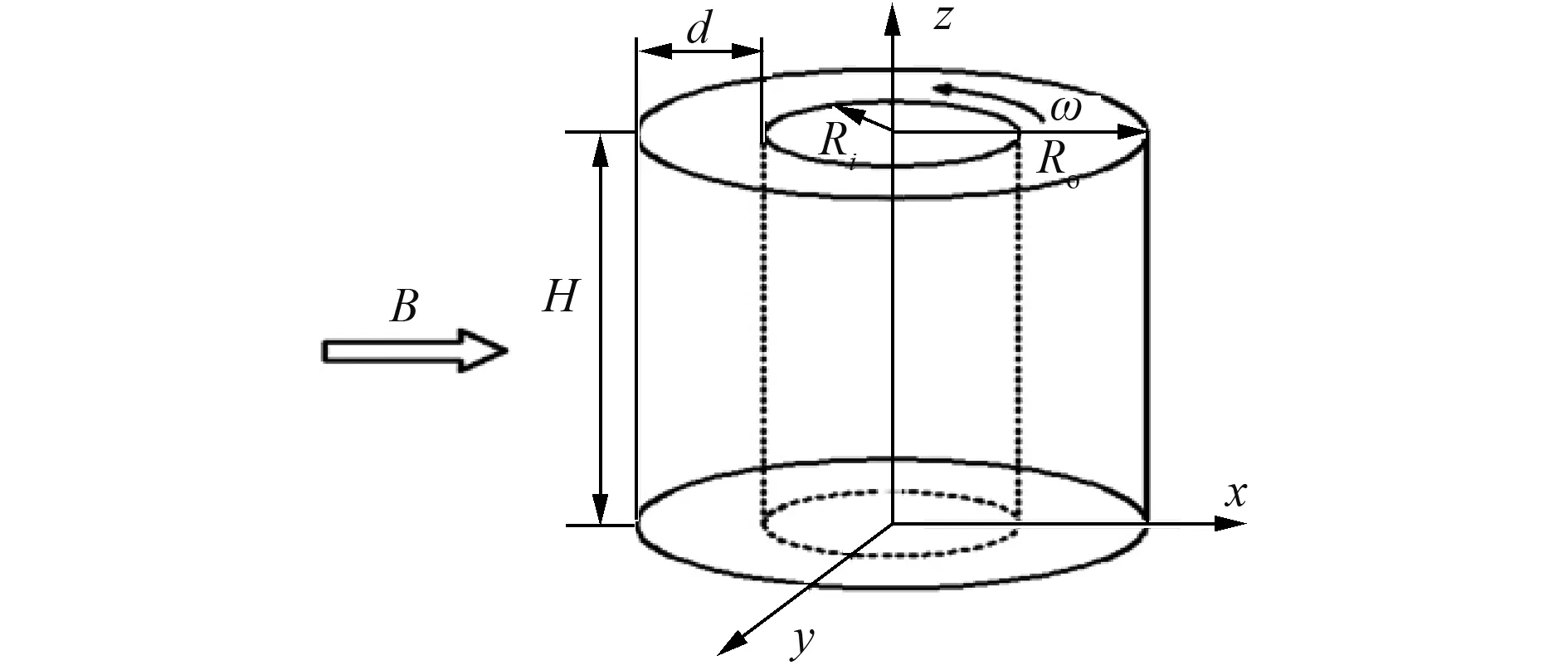
图1 模型示意图Fig.1 Physical model

1.2 控制方程

本文计算所用液体满足粘性不可压缩流体假设，流动控制方程如下：

连续性方程

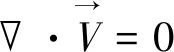
(1)

动量方程

(2)

电势方程

(3)

电场方程

(4)

感应电流密度方程

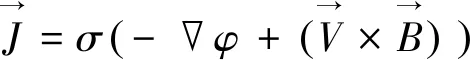
(5)

洛伦兹力方程

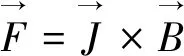
(6)

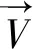
本文计算所用模型分为有限长和无限长模型，各壁面均为无滑移和电绝缘边界，具体如下：

r=Ri：uθ=ωRi，ur=uz=0，φ=0

r=Ro：uθ=0，ur=uz=0，φ=0

对于无限长度模型，上下壁面为周期性边界条件。对于有限长度模型，上下壁面边界条件如下：

z=0：uθ=ur=uz=0，φ=0

z=H：uθ=ur=uz=0，φ=0

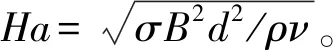
1.3 物理参数

本次计算中，选取雷诺数Re=10和Re=259，哈特曼数Ha=0～50。液镓物性参数如表1所示[17]。

表1 液镓(Ga)物性参数

1.4 网格无关性和有效性验证

采用六面体网格对模型进行划分，由于内外壁面处速度梯度较大且考虑哈特曼层的影响，轴向和周向网格均匀划分，径向网格划分如图2所示，由壁面向中心区域网格尺寸成比例增加。径向、轴向和周向网格数量分别选取为40×120×94、50×160×126、和60×200×158，对Re=10和Re=259在Ha=0的工况进行计算，结果如图3所示。可以看出对于有限长模型和无限长模型，在Re=10和Re=259工况下，径向、轴向和周向网格数量为50×160×126时，计算结果较为准确。

图2 网格划分示意图Fig.2 Schematic diagram of meshing

为了验证计算方法的可靠性，建立与文献[13]相同的物理模型，模拟轴向磁场作用下导电液体Taylor-Couette流动的演化过程。图4给出了Re=100，Ha=0和Ha=5工况下，子午面周向速度云图。可以看出，本文计算结果与文献结果相同，证明了本文计算方法的可靠性。

2 结果与讨论

内圆筒转速不同时，垂直环形间隙内的流体呈现出复杂的流动状态。为研究低雷诺数工况下导电液体在均匀横向磁场作用下的运动规律，雷诺数选取为Re=10和Re=259。为了直观的显示涡结构演化过程，选用Q准则对流场中的涡进行识别[18]。

2.1 Re=10工况

Re=10，环形间隙内液体流动为层流Couette流动。针对不同模型条件，研究导电液体在横向磁场作用下的运动规律。磁场强度为Ha=0～50，磁场方向沿x轴正向，如图1所示。

2.1.1 有限长模型

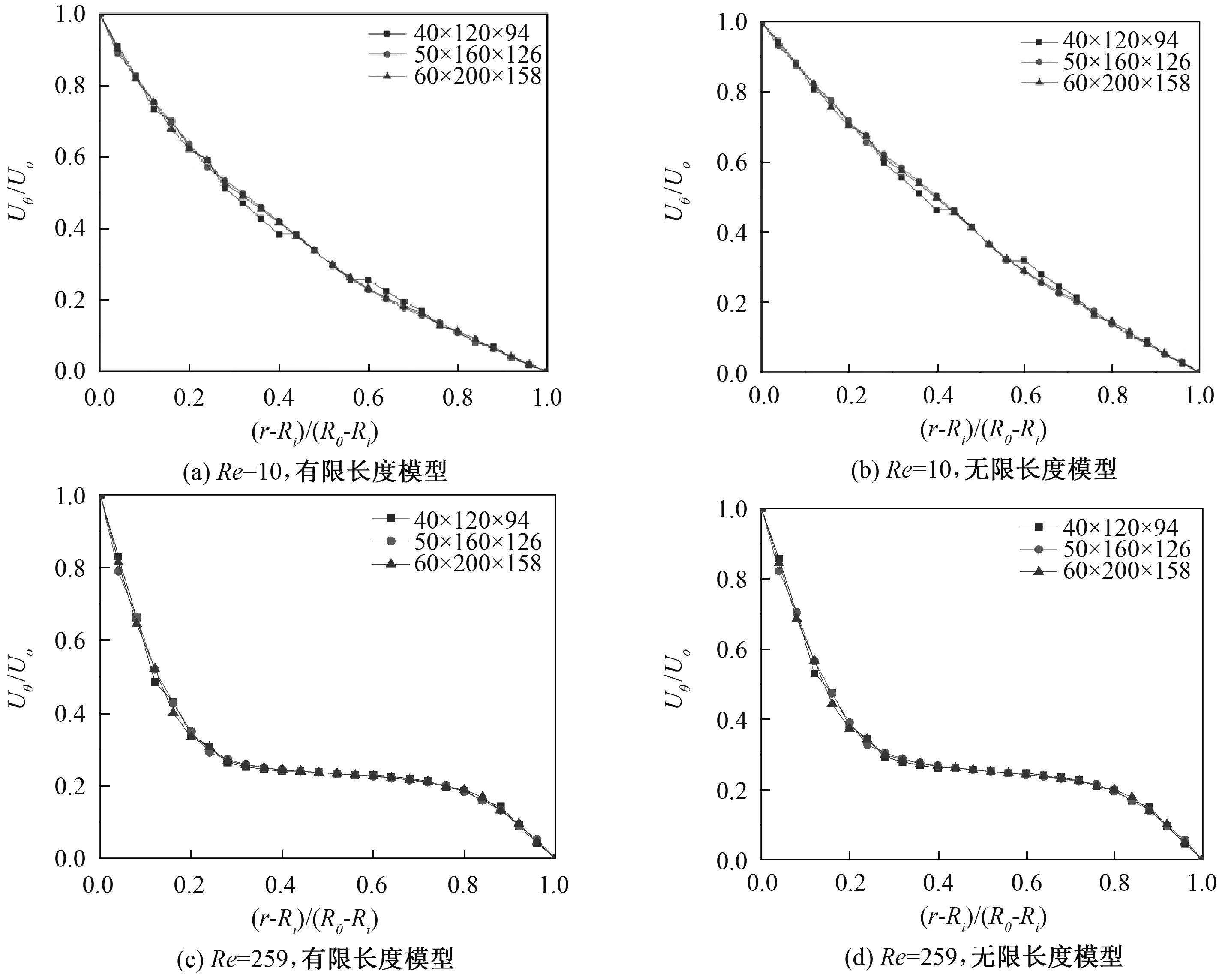
图3 周向速度分布曲线Fig.3 Distribution of azimuthal velocity

图4 周向速度等值线图Fig.4 Contours of azimuthal velocity

在横向磁场的作用下，导电液体的流型会随着磁场强度的增加发生一系列的变化，如图5所示。取Z=Γ/2截面进行分析，Ha=0时，周向速度具有轴对称性。加载磁场后， 周向速度变为沿x轴对称分布。由径向速度云图和涡型图可以看出，在磁场的作用下，产生一对关于x轴对称的涡。随着磁场强度增加，涡沿着轴向方向增长，直至充满整个模型。同时涡由圆环外侧逐步向内侧移动，并呈现出扁平化趋势。在Re=10，Ha=20工况下，Q准则显示的涡型图和Z=Γ/2截面的速度矢量图，如图6所示。可以看出两种方法均可以显示涡的形态，但Q准则更加直观，进一步证明了本文采用Q准则的合理性。

2.1.2 无限长模型

横向磁场加载到无限长模型，流型变化趋势与有限长模型基本相同，如图7所示。随着磁场强度的增加，涡从外圆筒移动到内圆筒，且逐渐扁平化。可以看出，涡的形状在轴向不发生变化，符合无限长模型的基本特点。

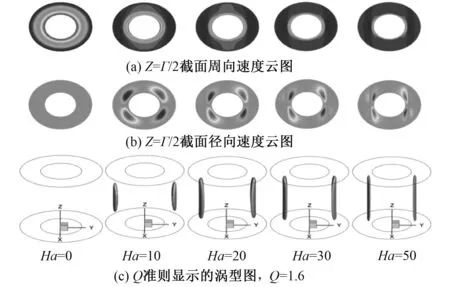
图5 Re=10工况下有限长模型内流型演化过程图Fig.5 Diagram of flown pattern evolution process in a finite length model at Re=10

图6 涡结构示意图Fig.6 Schematic diagram of vortex structure

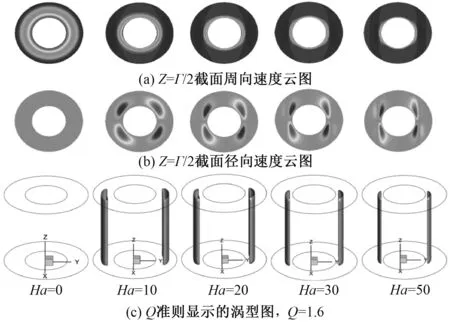
图7 Re=10工况下无限长模型内流型演化过程图Fig.7 Diagram of flown pattern evolution process in an infinite length model at Re=10

2.2 Re=259工况

模型半径比为η=1/2时，形成泰勒涡的临界雷诺数为Re=68.2[19]。本文选取Re=259，未加载磁场时，模型内形成2对稳定的泰勒涡，与Smieszek等人[20]的文献结论一致，证明了计算结果的可靠性。

2.2.1 有限长模型

将横向磁场加载到有限长模型，泰勒涡演化过程如图8所示。Ha=0～5时，流场内存在2对泰勒涡，随着磁场强度增大，泰勒涡尺寸变小，并逐渐向上下壁面靠近。Ha=6～10时，流场内出现3对泰勒涡，涡在磁场的作用下继续缩小，中间位置处的泰勒涡首先发生破裂。Ha=11～15时，上下壁面处泰勒涡破裂，泰勒涡进一步被磁场抑制，最终完全消失。

2.2.2 无限长模型

图9给出了无限长模型Taylor-Couette流动在横向磁场作用下的演化过程。Ha=0～3时，流场内存在2对泰勒涡。Ha=4时，流场内泰勒涡由2对变为3对，有限长模型对应的哈特曼数为Ha=6。Ha=4～8时，泰勒涡尺寸减小，但结构相对完整。Ha≥9时，泰勒涡逐渐破裂，最终消失。在这个过程中，流场内的每对泰勒涡演化过程一致，与有限长模型内的泰勒涡演化过程明显不同。

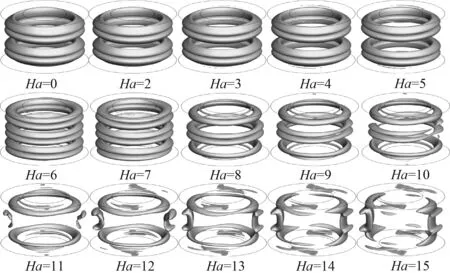
图8 Re=259工况下有限长模型内泰勒涡演化过程图(Q=16)Fig.8 Diagram of taylor vortex evolution process in a finite length model at Re=259,Q=16

3 结 论

横向磁场作用下垂直环形内导电液体随着雷诺数和哈特曼数的不同呈现出复杂的流动状态。对于不同的模型条件，流动过程也明显不同。具体结论如下：

(1)Re=10工况，流体为层流Couette流动。在磁场作用下周向速度分布由轴对称变为非轴对称，并出现一对关于x轴对称的涡，随磁场强度增加，涡由圆环外侧向内侧移动，并呈现扁平化趋势。

(2)Re=259工况，流体为Taylor-Couette流动。泰勒涡被磁场抑制，尺寸变小，由2对增加至3对，随磁场强度增加逐渐破裂，直至完全消失。

(3)Re=259工况，有限长模型内泰勒涡由2对增加至3对的磁场强度为Ha=6，泰勒涡完全破裂的磁场强度为Ha=15。无限长模型条件下对应的磁场强度分别为Ha=4和Ha=12。通过对比分析发现，磁场对有限长模型内导电液体的Taylor-Couette流动抑制作用稍弱，可以归咎为端部效应的影响。