基于相关机会目标规划的主动配电网日前优化调度

赵书强， 韩 雷， 李志伟， 杨宇航， 马舒婷

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

随着能源危机和环境污染问题的日益严重，以风电、光伏为代表的分布式电源大量分散的接入配电网，给配电网安全稳定运行带来了巨大挑战[1-3]。为应对这些挑战，主动配电网技术应运而生。然而，不同于火电和水电等常规能源，风电和光伏具有较强的不确定性。如何考虑源荷双侧的不确定性，制定安全经济的主动配电网调度计划，是一个亟需研究的问题。

国内外学者对该问题进行了大量研究。文献[4-5]采用基于模型预测控制的多时间尺度动态优化调度方法，通过短时间尺度的优化减少长时间尺度预测误差对主动配电网的影响。文献[6-7]采用场景法应对日前可再生能源出力、负荷和电价的不确定性。文献[8-9]针对可再生能源出力的不确定性，建立了鲁棒优化模型。文献[10-11]采用多场景和多时间尺度相结合的优化方法，在长时间尺度采用场景法应对源荷双侧的不确定性，在短时间尺度通过计划调整进一步减小预测误差的影响。文献[12-13]在主动配电网的优化调度模型中，引入负荷侧需求响应，来应对网络中的不确定性，进一步提高了主动配电网运行的经济性和可靠性。主动配电网的日前调度应该考虑功率的调整量，否则一旦功率调整过大，将增加日内滚动调度的压力和综合成本[14]，从而影响配电网的安全经济运行。

上述文献在日前调度阶段未考虑功率的调整量，或者基于场景法在目标函数中计入功率调整量的函数：交易计划偏差惩罚、功率调整量或日内调度成本。对于前者，当计入功率调整量后，日前调度计划未必是最优的；对于后者，为了提高计算速度，需要对场景进行削减，这将不可避免的带来不确定性信息的丢失。

基于此，本文引入功率概率性平衡的概念[15]，在日前调度阶段考虑功率的调整量，提出了一种含机会约束条件的基于相关机会目标规划的主动配电网优化调度模型。该模型在功率平衡方程、可再生能源容量约束中计入不确定性变量，以高优先级优化代表功率平衡的机会函数，以低优先级优化配电网的运行成本。经确定性转化后，该模型可以采用商用求解器进行求解。最后，采用修改的IEEE33仿真算例对所提模型的有效性进行验证。

1 源荷的不确定性

目前的研究大多都以确定性预测值和不确定性预测误差来表征系统中的不确定性变量。因为预测值是确定性的，对系统不确定性的描述主要体现在对预测误差的描述。

1.1 风电出力预测误差

风电出力与地形、风速及(离地)高度等自然因素有关，导致其各时刻的实际出力难以准确预测。通常认为风电功率预测误差服从正态分布[16]。基于此，t时刻的风电功率预测误差εW,t的概率密度函数为

(1)

式中：μW,t、σW,t分别表示t时刻风电功率预测误差的期望和标准差。

1.2 光伏出力预测误差

光伏系统通过逆变器并网运行，为最大限度的利用太阳能，光伏逆变器一般采用最大功率追踪控制模式，因此光照强度的预测精度直接决定了光伏出力的预测精度。目前关于光伏出力预测的研究较为丰富，通常认为光伏出力的预测误差服从正态分布[17]。其概率密度函数为

(2)

式中：μPV,t、σPV,t分别表示t时刻光伏功率预测误差的期望和标准差。

1.3 负荷预测误差

负荷预测误差往往难以避免。通常认为负荷预测误差服从正态分布[18]，负荷预测误差的概率密度函数为

(3)

式中：μload,t、σload,t分别表示t时刻负荷预测误差的期望和标准差。

1.4 系统预测误差

假设预测误差相互独立，由于各预测误差均服从正态分布，系统预测误差仍服从正态分布[19]。系统预测误差可表示为

εtotal,t=εload,t-εW,t-εPV,t

(4)

系统预测误差的平均值为各预测误差平均值的线性组合，方差为各预测误差方差之和。

2 相关机会目标规划基本理论

2.1 相关机会规划理论

为使某事件的机会函数在不确定性环境下达到最优，文献[20]提出相关机会规划理论(Dependent Chance Programming，DCP)。DCP的核心思想是制定最优决策使得随机事件在不确定环境下成立的概率最大。DCP的标准形式如下：

(5)

式中：ξ表示一个随机向量参数；x表示一个n维决策向量；hk(x,ξ)≤0,k=1,2,…q表示事件；gj(x,ξ)≤0,j=1,2,…,p表示不确定环境；Pr{·}表示事件成立的概率。

上式可表述为在不确定环境下求解一组最优决策量，使得含有不确定因素的事件成立的概率极大化。

2.2 相关机会目标规划理论

目标规划的本质为多目标优化问题的一种妥协模型。在实际的多目标优化问题中，目标之间并不相容，一个目标若想实现最优往往需要牺牲另一些目标。因此目标规划理论根据目标的重要程度建立优先结构，以此优先结构为基础对多个目标进行排序，从而尽可能地实现更多目标。相关机会目标规划D-CGP(Dependent-Chance Goal Programming)的标准形式[21]如下：

(6)

(7)

3 基于相关机会目标规划的主动配电网日前调度模型

3.1 含不确定变量功率平衡方程的处理

电力系统中最基本也最重要的是要满足电能供需平衡，在主动配电网的日前调度计划中需加入功率平衡约束。考虑源荷双侧的不确定性，功率平衡方程为

(8)

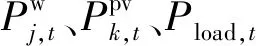
含不确定变量的功率平衡等式方程，难以直接求解。为此，引入概率性功率平衡的概念，将功率平衡等式约束松弛为含有不平衡量σt的不等式约束[15]，并以概率的形式表示：

(9)

最大化此事件成立的概率，其优化过程是通过调整交换功率、可控分布式电源或可中断负荷功率，使电能供需偏差处于可行集范围之内的概率最大。这是一个在不确定环境下极大化随机事件发生概率的问题，与相关机会规划问题契合。

3.2 目标函数与控制变量

主动配电网通常含有不同类型、不同容量的分布式电源，本文考虑这些电源均为配电网所属电力公司所有。调度时间间隔为1 h，优化控制变量主要包括：风电、光伏的无功出力、可控分布式电源的有功无功出力和可中断负荷有功。

通过控制上述变量，调度模型以高优先级优化代表功率平衡的机会函数，以低优先级优化配电网的运行成本。目标函数如下：

(10)

F2=min(Cgrid+CDG+CESS+CCL)

(11)

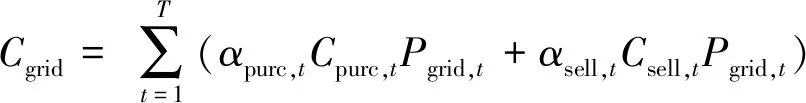
(13)

(14)

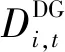
根据相关机会目标规划理论，考虑目标的优先级和目标值，模型的实际目标函数为

(15)

3.3 约束条件

主动配电网的约束条件主要包括潮流约束、网络安全约束和分布式电源的有功无功出力约束。

3.3.1 潮流约束

(16)

(17)

3.3.2 网络安全约束

(18)

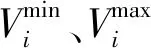
3.3.3 可控机组出力约束

可控机组运行的约束主要包括机组出力约束、爬坡约束和最小启停时间约束：

(19)

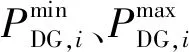
3.3.4 储能出力约束

储能运行约束主要包括充放电功率约束和荷电状态约束。

(20)

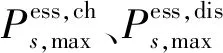
3.3.5 容量约束

分布式电源分为可控分布式电源和可再生能源。可控分布式电源出力受控，容量约束为确定性约束：

(PDG,j,t)2+(QDG,j,t)2≤(SDG,j,t)2

(21)

而可再生能源有功出力具有不确定性，使得容量约束含有不确定性变量。以逆变型电源为例，容量采用机会约束条件的形式：

Pr{(PRE,j,t+εRE,j,t)2+(QRE,j,t)2≤(SRE,j,t)2}≥β

(22)

式中：PRE,j,t表示t时刻可再生能源j的出力预测值；εRE,j,t表示t时刻可再生能源j出力预测误差；β为机会约束成立的置信水平。

3.4 模型求解

由于目标函数和约束条件中存在不确定性变量，模型难以直接求解。为了消除不确定性变量，本文对调度模型进行确定性转化。

目标函数中，系统预测误差为不确定性变量，其他量为确定性变量。由于系统预测误差服从正态分布，最大化式(10)成立的概率相当于最小化确定性变量与系统预测误差平均值的偏差。据此，可实现目标函数的确定性转化：

F1,t=min|psure,t-E(εtotal,t)|

(23)

式中：psure,t为t时刻确定性变量的和；E(εtotal,t)为t时刻系统预测误差的均值。

由于式(23)取最小值，相应的目标值可取0。

对于容量机会约束条件，则可根据采样原理进行转化[24]：

(24)

经过上述确定性转化之后，本文提出的模型转化为含整数变量的二阶锥优化模型，可以采用成熟的商业软件求解，从而提高求解效率。

4 算例分析

本文对IEEE33节点系统进行修改，算例系统及参数详见附录。算例采用Yalmip进行仿真系统建模，调用商用求解器Cplex(版本12.5)进行求解，计算环境为Intel(R)Core(TM)i5-4210M 2.6 GHz，4G内存。

4.1 日前优化调度结果

采用本文提出的主动配电网日前优化调度模型，制定的有功调度计划如图1所示。

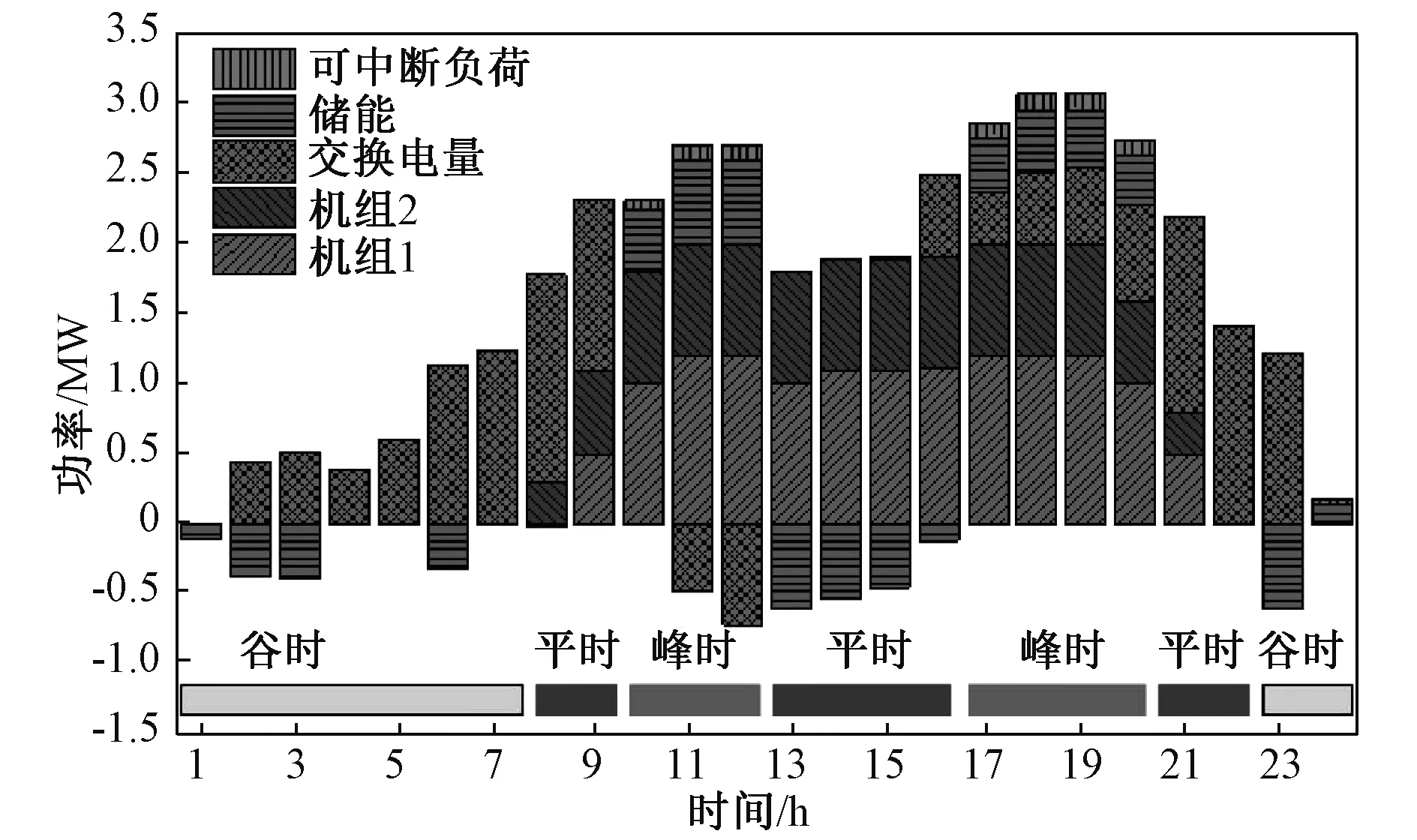
图1 日前有功调度计划Fig.1 Day-ahead active dispatch plan

可以看出，谷时段主动配电网向上级电网购电，燃气机组不出力，储能进行充电。该时段负荷处于低谷，购电成本较低，燃气轮机停机，储能处于充电状态，通过购电和风电满足负荷需求比较经济；平时段燃气机组出力随着负荷的变化而变化。该时段负荷处于一般水平，燃气轮机的发电成本小于购电成本，通过燃气轮机供电比较经济；峰时段燃气机组、储能几乎处于满发状态，可中断负荷处于削减状态，并且当电能过剩时向上级电网售电。该时段负荷处于高峰，购电成本很高，售电成本也高，充分利用主动配电网的分布式电源发电、削减负荷或向上级电网售电，能提高配电网运行的经济性。

4.2 电能供需偏差分析

为分析功率平衡方程处理方式对电能供需偏差的影响，采用两种调度模型进行对比。模型1：确定性功率平衡优化调度，在功率平衡方程中不计入预测误差；模型2：本文所提含机会约束的基于相关机会目标规划的优化调度。在风电和光伏预测值的基础上计入预测误差，采用拉丁超立方抽样方法生成代表次日的1 000种场景。不考虑日内交换功率、可控分布式电源或可中断负荷功率调整，将调度计划在生成的场景中模拟运行，观察调度计划的电能供需偏差。

图2为两种调度计划的电能供需偏差。可以看出，两种调度计划电能供需偏差的最大值分别为0.56 MW和0.36 MW。可见，与调度计划1相比，调度计划2降低了电能供需偏差的最大值。

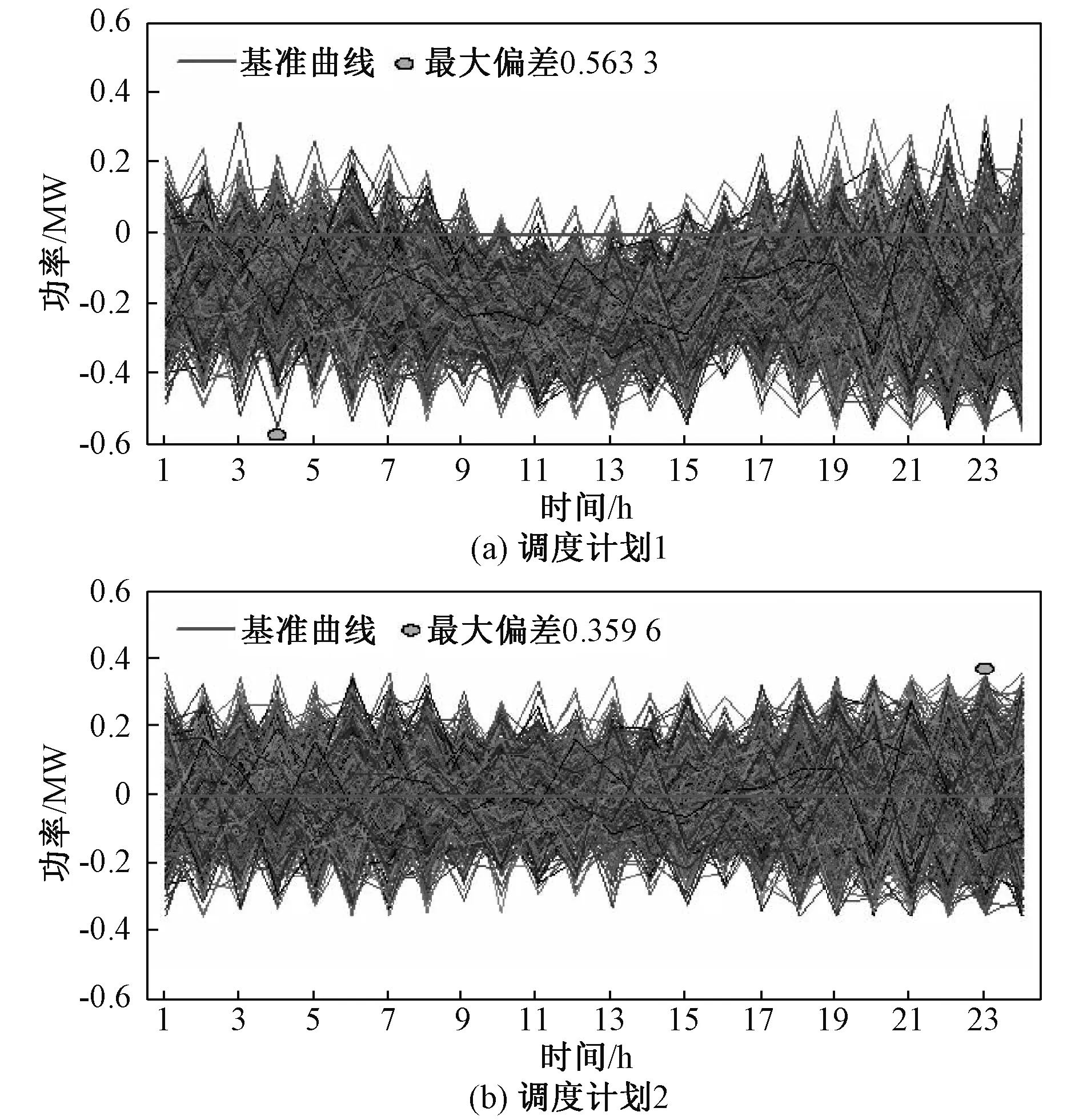
图2 两种调度计划电能供需偏差Fig.2 Electric energy deviation of supply and demand in two dispatching plans

为了进一步比较电能供需偏差的大小，引入曲线欧式距离的概念，该值表征曲线的相似程度，距离越小越相似。记第i条曲线Xi=(xi1，xi2，…，xip)，(i=1,2，…n)，则曲线Xi和Xj的欧式距离为

(25)

式中：i和j为曲线编号，i=1,2，…，n，j=1,2，…，n；k为曲线分量的序号，k=1,2，…，p。

理想情况下，各时刻电能供需偏差均为0，令X0=(0,0，…，0)为基准曲线。在此基础上，可由式(25)计算电能供需偏差曲线至基准曲线的距离，并能进一步计算多条电能供需偏差曲线至基准曲线的平均距离。将多条曲线称为簇。电能供需偏差曲线簇至基准曲线的平均距离越小，表示电能供需偏差曲线簇与基准曲线越相似。

两种调度计划电能供需偏差曲线簇至中心曲线的平均距离分别为1.05 MW和0.57 MW，调度计划2电能供需偏差曲线簇与基准曲线更相似。

根据上述两个指标可知：与调度计划1相比，调度计划2能降低电能供需偏差。以高优先级优化代表功率平衡的机会函数，整个优化过程相当于调整交换功率、可控分布式电源或可中断负荷功率，使包含风电、光伏在内的电源功率与负荷功率相匹配的概率最大。由于多了该优化过程，调度计划2能减小电能供需偏差，从而减少功率的调整量。

4.3 容量越限概率分析

为分析约束处理方法对容量越限概率的影响，采用两种约束条件进行对比：确定性约束和机会约束条件。以光伏为例，假设光伏出力预测值为1 MW，预测误差均值分别为预测值的-10%、-5%、0、5%和10%，标准差分别为预测值的2%、4%和6%，采用拉丁超立方抽样方法分别生成代表次日光伏出力的1 000种场景。

采用确定性约束，根据式(21)计算无功限值为1.118 Mvar。假设光伏按最大无功限值出力，在生成的场景中模拟运行。通过统计容量越限的场景数，计算容量越限的概率。由于考虑了最恶劣的工况，该概率实际为容量越限的最大概率。表1为预测误差不同分布参数下容量越限的最大概率。可以看出，容量越限的最大概率为76.0%，最小概率为24.0%。可知，采用确定性约束，不能很好的控制容量越限的概率，可能发生大概率容量越限的事件。

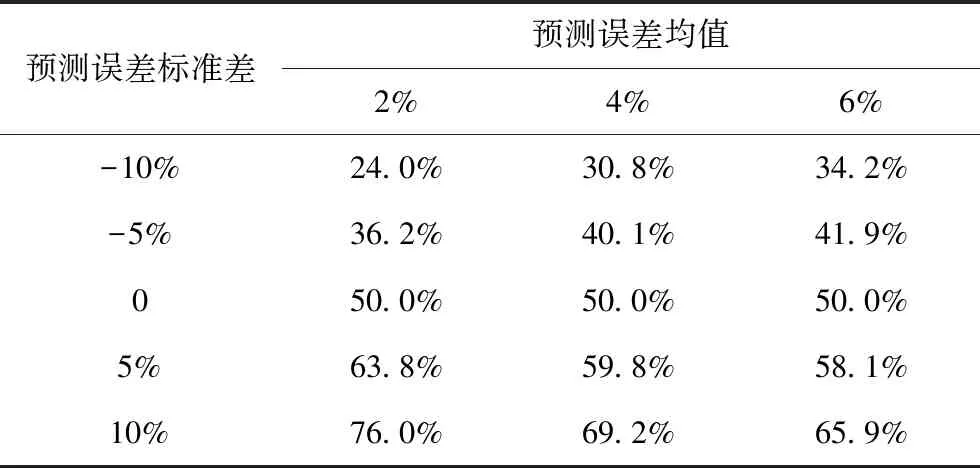
表1 容量越限的最大概率

5 结 论

本文在功率平衡方程、容量约束中计入不确定性变量，提出了一种含机会约束条件的基于相关机会目标规划的主动配电网优化调度方法。得到如下结论：

(1)采用本文提出的基于相关机会目标规划的日前调度方法，能减少日内功率调整量，在应对源荷双侧不确定性方面具有优势。

(2)对于可再生能源容量约束，采用机会约束能更好的控制容量越限的概率，从而减少因视在功率越限而被迫调整无功的概率。