区分优先级业务的非对称两级轮询系统特性分析
杨志军,毛 磊,丁洪伟,刘 征
(1.云南大学 信息学院,云南 昆明 650500;2.云南省教育厅 教育科学研究院,云南 昆明 650223)
0 引 言
物联网作为感知互联系统向物理世界的延伸,极大地拓展了人类对物理世界的认识和感知能力,其广泛应用必将深刻地影响人类的生活方式[1]。感知层作为物联网的重要组成部分,利用各种智能传感器和感知设备实时采集各类信息,然后通过接入网络,实现人与物、物与物之间的内在联系。物联网中各类传感器在采集信息时,系统内存在多种不同的信息,如声、光、生物、位置等,各类信息在传输时又有不同的优先级。传统的轮询系统和并行处理方式很难区分这些业务,因此区分优先级和多业务的数据通信系统一直以来是物联网研究的热点。文献[2]基于无线传感器网络,提出一种两级优先级轮询控制方式用于森林防火,对险情级别进行划分,然后对所划分的级别实行两级优先级轮询服务,很大程度上提高了网络的利用率,但并没有对提出的模型进行解析。文献[3]中,针对宽带无线接入网络系统中信息分组传输控制的实时性和公平性要求,提出基于优先级的两级对称轮询系统,并对其性能进行了精确解析。文献[4]提出一种具有可变数据包长度的无线多媒体局域网轮询策略,该策略可以同步信息分组的轮询和传输。
上述研究都是在网络中数据以离散时间到达的基础上[5-7]展开的,而且主要集中在区分优先级方面,并未对不同业务进行区分。物联网中,感知层内涉及多种业务,在对多种业务进行信息采集时,不同业务提供的数据流和其优先级一般不同。同时,很多时候往往需要收集各个节点一段连续时间的数据变化,而不是某一个时刻的信息,因此,研究连续时间的非对称两级轮询系统具有很大意义。
轮询作为一种重要的数据传输控制策略和调度方式,在通信网络中有着广泛应用[8-10]。其服务规则主要有完全服务、门限服务和限定服务三种,按照各个终端数据到达的方式又分为对称的和非对称的[11-12]。本文针对上述物联网的业务特点,提出连续时间非对称两级轮询策略,用于解决物联网多业务任务的数据传输问题,普通节点采用非对称完全服务方式,高优先级节点采用门限服务方式。然后利用嵌入式马尔可夫链和概率母函数的方式构建数学模型分析其性能,并通过计算机仿真进行验证。
1 系统模型
对物联网的感知层进行建模,该系统主要由一个中继节点(服务器),N+1 个采集节点组成。N+1 个采集节点又分为N个普通节点和一个高优先级节点(中心节点)。高优先级节点接受服务时,采用门限服务方式,服务器仅对当前时段到达节点的数据包提供服务,服务期间到达的数据则继续在存储空间中等待下一次服务。对于高优先级节点,在每次服务过程中,节点的各项参数都是固定的,采用门限服务方式可以实现资源的合理配置。普通节点采用非对称完全服务方式,服务器不仅对当前时段到达的数据包进行服务,还要对服务期间到达的数据服务,直到节点为空,才切换到高优先级节点进行服务。N个普通节点代表N种不同的业务或数据,每个节点数据包到达的速率、服务器对每个数据包的服务时间和服务器的切换时间都是不同的,完全服务方式使每个节点的时延都很小。
系统模型如图1 所示,服务器对站点的查询顺序为,首先查询高优先级节点(即中心节点,用h表示),服务完成后切换到第i号普通节点。服务过程中,中心节点采用并行控制方式,就是在服务当前节点的同时,服务器利用捎带查询技术查询下一个需要信息数据发送服务的普通节点,这样将不再消耗系统的转换查询时间,不仅提高了系统的利用率,而且降低了系统的平均时延[3]。服务完i号普通节点后又经过一个切换时间,切换到中心节点服务,然后再切换到i+1 号普通节点。
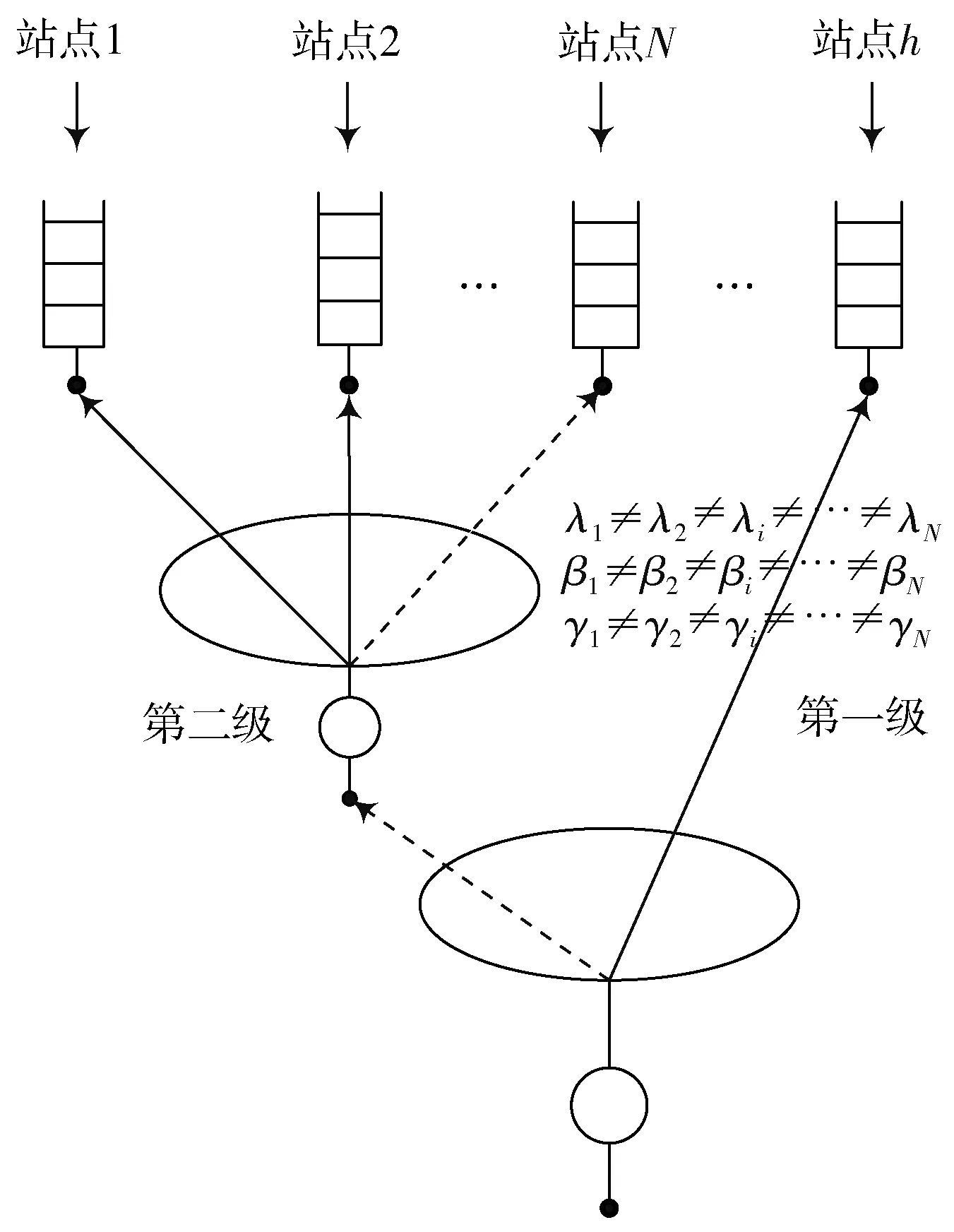
图1 系统模型
1.1 系统工作条件
根据轮询系统的工作模式和特点,对其工作条件进行如下定义:
1)连续时间非对称两级轮询系统中,进入各个节点缓冲区等待发送的数据包服从独立同分布的泊松过程,普通节点到达率为λi,高优先级节点到达率为λh。
2)每一个站点在接受服务时发送一个信息分组所需的时间服从独立、同分布的概率分布,其概率母函数为(si),均值和二阶原点矩分别为
3)服务器从普通节点向高优先级站点的转换时间服从独立、同分布的概率分布,其概率母函数为(si),均值和二阶原点矩分别为
4)假设每一个节点的缓冲区无限大,服务器按照数据到达的先后顺序对数据进行传输。
5)整个系统工作在连续时间状态。
1.2 变量定义
设tn时刻服务器为第i号普通节点提供服务,随机变量ξi(n)表示tn时刻缓冲区存储的数据量,ξh(n)表示高优先级站点tn时刻存储的数据量,则tn时刻整个系统的状态变量为{ξ1(n),ξ2(n),…,ξN(n),ξh(n)}。tn*时刻服务器切换到高优先级节点提供服务,此时系统的状态变量为{ξ1(n*),ξ2(n*),…,ξN(n*),ξh(n*)}。tn+1时刻又切换到i+1 号普通节点提供服务,系统的状态变量为{ξ1(n+1),ξ2(n+1),…,ξN(n+1),ξh(n+1)},其 中,tn<tn*<tn+1。
由此可得下列关系式:
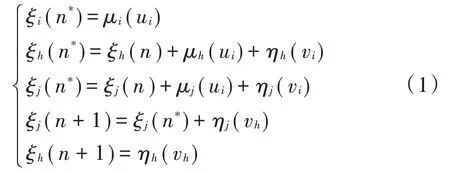
式中:ui表示服务器从i号普通节点转向高优先级节点的查询转换时间;vi表示服务器对i号普通节点进行完全服务的服务时间;vh表示服务器对高优先级点进行门限服务的服务时间;μh(ui)表示在ui时间内进入高优先级节点h的数据量;ηh(vi)表示在vi时间内进入高优先级节点h的数据量;μi(ui)表示ui时间内进入i号节点的数据量;μj(ui)表示ui时间内进入j号节点的数据量;ηj(vi)表示vi时间内进入j号节点的数据量。
研究发现,系统内tn+1时刻的状态变量只与tn时刻有关,在该系统内,节点数量是相对确定的,即系统的状态变量是有限的,因此可用马尔可夫链来描述该过程。该马尔可夫链在条件下达到稳定状态,系统稳定时,其概率母函数定义如下:

2 系统的特性解析
2.1 平均排队队长
定义:系统的平均排队队长g~i(j)为tn时刻i号节点接受服务时,j号节点内平均存储的数据量,则:
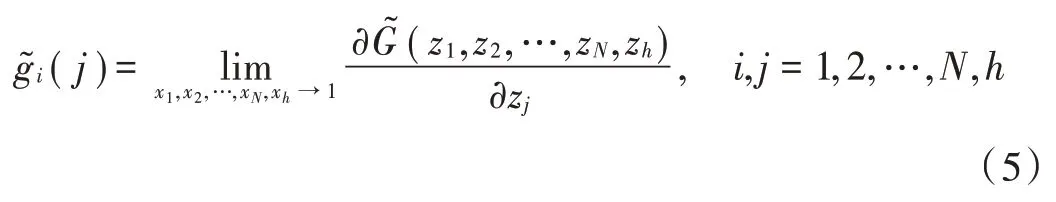
由式(3)~式(5)可得普通节点的平均排队队长为:

式中ρi=λi βi,i=1,2,…,N。
2.2 平均查询周期
连续时间非对称两级轮询系统的轮询周期定义为服务器两次查询同一站点的时间间隔,具体表述为服务器对系统中的N+1 个站点按服务规则完成一次服务所花费的时间。通过计算得到:

2.3 平均时延
定义:连续时间非对称两级优先级轮询系统的平均时延等于数据包到达节点直到该数据包被发送出去所花费的时间,用E[w]表示。可以通过对概率母函数求二阶偏导获得,如式(9)所示,这里仅通过仿真实验得出普通节点和高优先级节点的平均时延,并未对其进行详细推导。
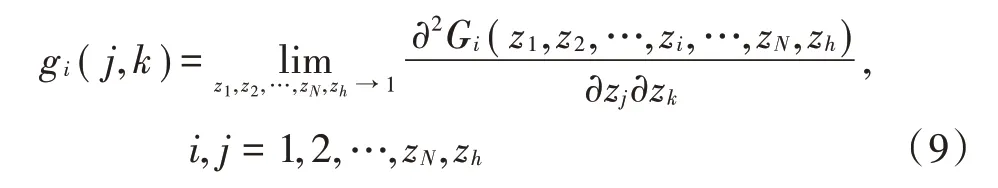
2.4 系统吞吐量
吞吐量为单位时隙内系统所能服务的数据量。
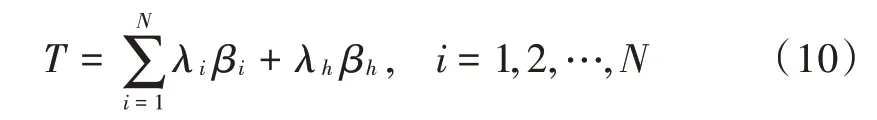
3 仿真实验及其分析
上述采用数学分析的方法对连续时间非对称两级轮询系统的平均排队队长、平均查询周期等性能参数进行推导。为了验证方法的可行性,根据2.1 节给出的条件,在Matlab 2018a 上建立系统模型进行数值计算和实验仿真。
实验中设置5 个普通节点,1 个高优先级节点(中心节点),其中,1~5 号是普通节点,6 号是中心节点,各个节点的初始参数如表1 所示。

表1 模型基本参数
图2 和图3 是5 个普通节点接受非对称完全服务时平均排队队长随数据包到达率和服务时间的变化关系。从图中可以看出,理论值与实验值基本是一致的,说明理论分析的合理性。普通节点的平均排队队长与数据包的到达率和服务器对数据包的服务时间呈现正相关的关系,即平均排队队长随到达率和服务时间的增加而增大。当到达率和服务时间在较小范围内时,平均排队队长增长较为缓慢;随着服务时间或到达率的增加,平均排队队长增长较为迅速。这是因为系统的负载是有限的,随着到达率或服务时间增加到一定值,系统的处理能力达到饱和,这个时候继续到达的数据包将会一直滞留在系统内,从而导致数据的平均排队队长急剧增加,当到达率一定时,服务时间越长,平均排队队长越大。
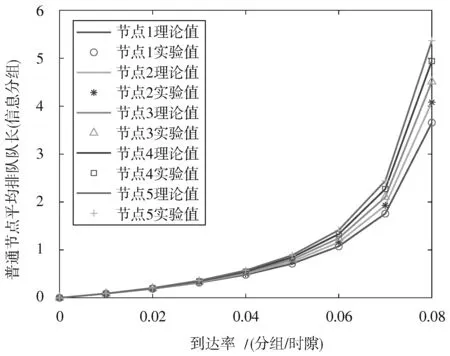
图2 普通节点平均排队队长与到达率的关系

图3 普通节点平均排队队长与服务时间的关系
图4 和图5 是中心节点接受门限服务时平均排队队长随到达率和服务时间的变化关系,与普通节点一样,平均排队队长随着到达率和服务时间的增大而增加。每个普通节点切换到中心节点的平均排队队长都不同,是因为非对称引起的各个节点数据的到达率不同,结合式(7)可知,平均排队队长与到达率呈正比关系,到达率越小,对平均排队队长的影响越小。对比图2 和图3,可以看出,中心节点的平均排队队长增长缓慢,相同到达率和服务时间下,中心节点的平均排队队长远远小于普通节点。这说明该模型能够很好地区分不同业务的优先级,普通节点使用时延较小的完全服务,中心节点使用门限服务,中心节点中每次仅处理一定数量的数据,通过中心节点-普通节点的频繁切换,既保证了优先级业务能迅速得到服务,又降低了普通业务的时延性。
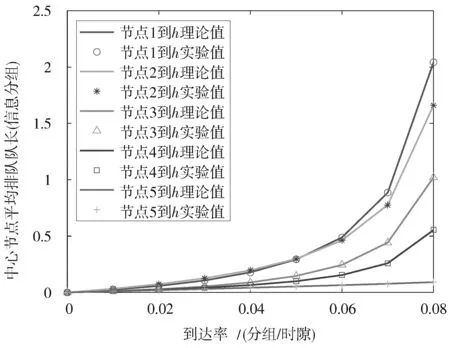
图4 中心节点平均排队队长与到达率的关系
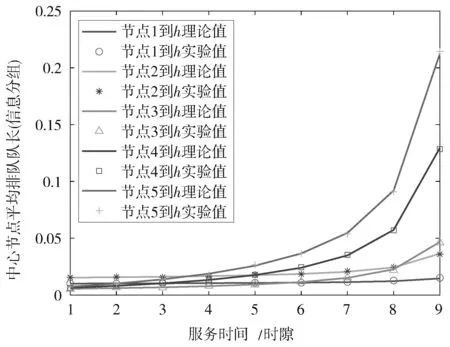
图5 中心节点平均排队队长与服务时间的关系
图6 展示了循环周期与到达率的关系,从图中可以看出,实验值与理论值基本拟合,循环周期随着信息分组到达率的增加而增大。当到达率很小时,系统很快就能对所有节点完成一次访问;当到达率逐渐增大时,循环周期急剧增加,在节点数较多的情况下,靠后的节点需要等待很长时间才能得到服务。因此,在实际应用中,系统的到达率最好是小于0.5,这样就能保证系统的服务质量。
图7 和图8 是普通节点和中心节点平均时延随系统负载的变化关系。图8 表示从5 个普通节点依次转换到中心节点时,中心节点数据包的平均等待时延。从总体上看,普通节点和中心节点的平均时延都是随着负载的增加而增大。当负载一定时,中心节点的平均时延远远小于普通节点,这说明该模型能对不同业务优先级进行区分。对比两个图中不同节点的平均时延,可以看出,普通节点和中心节点的平均时延变化趋势刚好相反,这正是该模型采用两级服务的体现。因为普通节点采用完全服务,当某一普通节点的平均等待时延较小时,到达的数据越多,相应的中心节点就需要等待更长的时间才能得到服务。
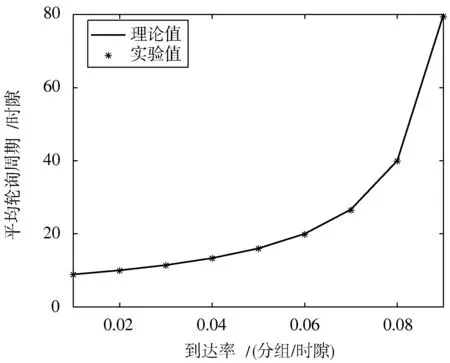
图6 循环周期与到达率的关系

图7 普通节点平均时延随负载的变化

图8 中心节点平均时延随负载的变化
表2 列出了离散时间门限-完全两级优先级非对称模型、非对称完全服务模型和本文模型的性能参数对比。从表中可以看出,在负载一定时,非对称完全服务的性能略优于本文模型。这说明高优先级节点的性能影响整个系统的性能,对系统划分不同优先级,让高优先级业务得到更多的服务,是以牺牲系统性能为代价的,当然这种牺牲很小。与离散时间两级优先级非对称模型相比,该模型的性能略好,这说明连续时间的两级优先级非对称模型在数据通信过程中的公平性和传输的时延方面都有较好的优势,同时也能处理优先业务,为系统提供更加优良的服务质量。
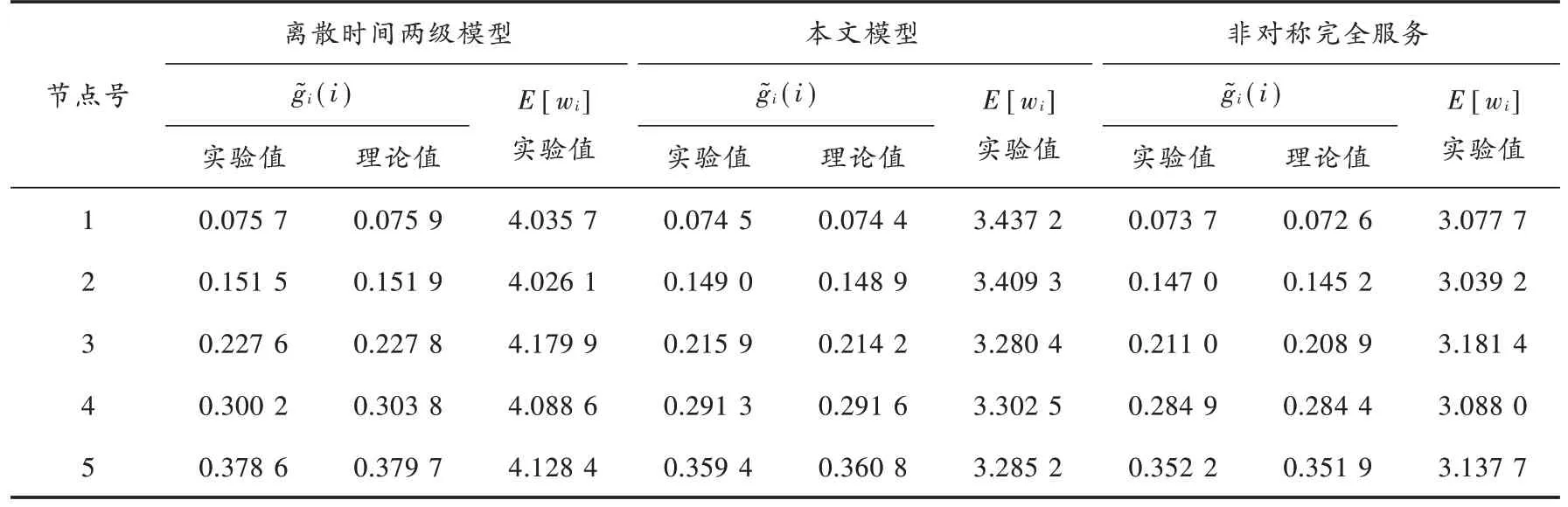
表2 三种模型性能对比
4 结 语
为了解决物联网中多优先级和多业务任务的需求,本文提出一种连续时间的非对称门限-完全服务模型。对物联网的感知层进行建模,将系统分为普通节点和高优先级节点。通过高优先级节点-普通节点的频繁切换区分不同业务,高优先级节点向普通节点切换时,采用并行处理方式提高系统效率。然后,运用嵌入式马尔可夫链理论和概率母函数的方法对该模型的平均排队队长、循环周期、吞吐量进行了详细解析。最后,根据理论分析条件,在Matlab 2018a 上构建其模型,对系统的各项性能参数进行仿真计算,得出实验值与理论值基本一致。分析表明,该模型在区分不同业务的同时,又能为高优先级业务提供优质量服务,提高了物联网的服务质量。与离散时间两级优先级非对称模型和非对称完全服务模型相比,该模型也表现出了较大优势。需要说明的是,该系统二阶特性、平均时延解析方法较为复杂,本文仅通过仿真实验进行了计算,在今后的工作中可以进一步对其进行计算,同时也可以拓展多种混合服务方式轮询系统的研究。

