PRECISE VALUES OF THE BLOCH CONSTANTS OF CERTAIN LOG-p-HARMONIC MAPPINGS∗
Mingsheng LIU(刘名生)Lifang LUO(骆莉芳)
School of Mathematical Sciences,South China Normal University,Guangzhou 510631,China E-mail:liumsh65@163.com;1617983549@qq.com
Abstract The aim of this article is twofold.One aim is to establish the precise forms of Landau-Bloch type theorems for certain polyharmonic mappings in the unit disk by applying a geometric method.The other is to obtain the precise values of Bloch constants for certain log-p-harmonic mappings.These results improve upon the corresponding results given in Bai et al.(Complex Anal.Oper.Theory,13(2):321-340,2019).
Key words Bloch constant;Landau theorem;Bloch theorem;biharmonic mappings;polyharmonic mappings;log-p-harmonic mappings;univalent
1 Introduction and Preliminaries
Suppose that p is a positive integer and F=u+iv is a 2p times continuously differentiable complex-valued mapping in a domain D⊆C.Then F is said to be polyharmonic(or pharmonic)in D if F(z)satisfies the p-harmonic equation
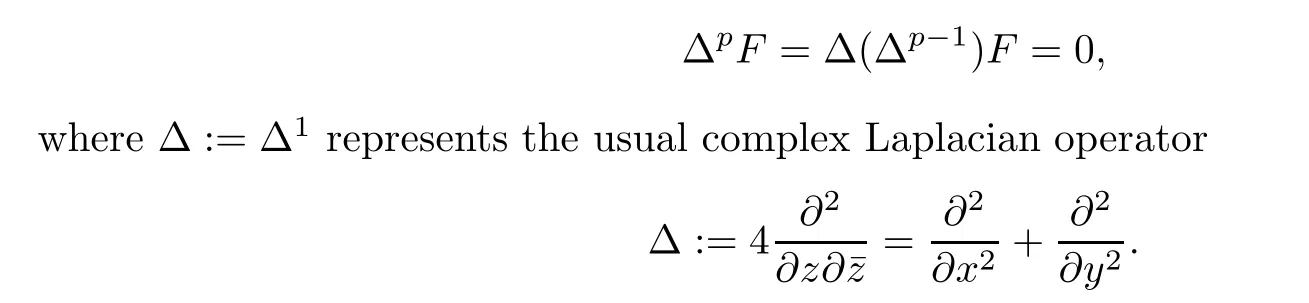
If D is a simply connected domain,then it is easy to see that a mapping F(z)is a p-harmonic mapping in D if and only if it can be written as
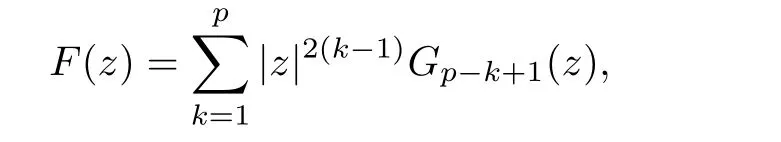
where Gis harmonic on D for each k ∈{1,2,···,p}.In particular,F(z) is a biharmonic mapping in a simply connected domain D if and only if it can be written as
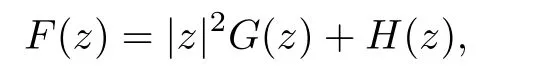
where G(z),H(z) are harmonic on D (cf.[1,7]).
A mapping f is called a log-p-harmonic mapping if log f is a p-harmonic mapping.When p=1,the mapping f is called log-harmonic.When p=2,the mapping f is called logbiharmonic (cf.[21]),and can be regarded as a generalization of holomorphic functions.Thus we say that f is called a log-p-harmonic mapping in a simply connected domain D ⊆C if and only if f has the form
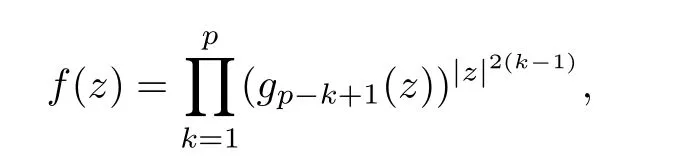
where each gis log-harmonic for k ∈{1,···,p} (cf.[21]).
For r >0,let U={z ∈C :|z| It is known(cf.[19])that a harmonic mapping is locally univalent if and only if its Jacobian Jdoes not vanish anywhere.A harmonic mapping f(z)on D is said to have bounded dilation if Λ(z)≤Λ for all z ∈D. For harmonic mappings in U,under a suitable restriction,the Bloch and Landau theorems were obtained by Chen et al.[4].Better estimates were given in [13],and later in [5,7–10,15,17,18,23–26,31,32].Recently,many authors also considered the Landau-type theorems for biharmonic mappings and p-harmonic mappings (see [2,3,6,7,11,16,20,22,27–30,33]),however there were few precise results.In 2011,Li and Wang[21]introduced the log-p-harmonic mappings,and derived a Landau-type theorem as follows: Liu et al.improved Theorem A in [27].In 2018,Bai et al.established in [3]the following new versions of Landau-type theorems: (i) G(z) is harmonic in U,and G(0)=0; (i) g(z) is log-harmonic in U,and g(0)=1; All of Theorems A,B and C are not sharp.In this article,we first establish the precise forms of the Landau-Bloch type theorems for certain polyharmonic mappings (see Theorems 3.1 and 3.2),which provide the precise form of Theorem B.Then,by applying Theorems 3.1,3.2 and Lemma 2.4,we derive the precise univalent radius and the accurate value of the Bloch constant for certain log-p-harmonic mappings (see Theorems 3.4 and 3.8),which provides the precise form of Theorem C. Moreover,if ρ is the biggest univalent radius of f(z),then the radius r=sinh σ is sharp. Figure 1 The graphical model of Lemma 2.4 Setting Ω={w=|w|e|e<|w| We first prove the precise form of the Landau-Bloch type theorem for certain polyharmonic mappings,which is one of the main results in this article. Theorem 3.1 For r ∈[0,1],considering the continuous function it is easy to verify that g(r) is strictly decreasing on [0,1],g(0)=1>0,and therefore,by the mean value theorem,there is a unique real number ρin (0,1/Λ]such that g(ρ)=0.Thus we have Next,we’re going to prove that F(U) contains a schlicht disk U.Notice that F(0)=0,and by Lemma 2.2 and (3.4),for each z∈∂U,we have Now we prove the sharpness of ρand σ.To this end,we consider a polyharmonic mapping F(z)which is given by (3.3).It is easy to verify that F(z)satisfies all hypotheses of Theorem 3.1,thus we have that F(z) is univalent in the disk U,and F(U)⊇U. To prove that the univalent radius ρis sharp,we need to prove that F(z)is not univalent in Ufor each r ∈(ρ,1],where ρis the unique root in (0,1) of the equation For such ε,we let x=ρ+ε,and there is a unique δ ∈(0,ρ)such that x:=ρ−δ ∈(0,ρ)and f(x)=f(x). This implies that Fis not univalent in Ufor each r ∈(ρ,1),which confirms the sharpness of ρ. Finally,note that F(0)=0,and picking up z=ρ∈∂U,it follows from (3.7) that Note that for harmonic mapping G(z)of U with G(0)=λ(0)−1=0,and Λ(z)≤Λfor all z ∈U,it follows from Lemma 2.3 that Λ≥1.Theorem 3.1 provides the precise form of the Landau-Bloch type theorem of certain polyharmonic mappings for the cases Λ,···,Λ≥0 and Λ>1.If Λ,···,Λ≥0,and Λ=1,then we prove the following precise form of the Landau-Bloch type theorem of certain polyharmonic mappings using Lemma 2.3: Theorem 3.2 be a polyharmonic mapping of U,where all Gare harmonic on U,satisfying G(0)=λ(0)−1=0 for k=1,2,···,p.If Λ(z) ≤1,and Λ(z) ≤Λ,k ∈{2,3,···,p}for all z ∈U.Then F(z) is univalent in U,and F(U) contains a schlicht disk U,where Proof Remark 3.3 Finally,we establish the precise form of Landau-Bloch type theorems for certain log-pharmonic mappings by applying Theorems 3.1,3.2,and Lemma 2.4,which constitutes the main result of this article.In particular,we obtain the accurate values of Bloch constants for certain log-p-harmonic mappings in U. (i) g(z) is log-harmonic in U,g(0)=1,and G:=log g; (ii) for each k ∈{2,···,p},Λ(z)≤Λ,and Λ(z)<Λfor all z ∈U. Then f(z) is univalent in U,where ρis the unique root in (0,1) of equation (3.1).Moreover,the range f(U) contains a univalent disk U(w,r),where σis given by(3.2),and Both of the radii,ρand r=sinh σ,are sharp. We know that and that f(0)=1,so it follows from g(0)=λ(0)=1 that G(0)=λ(0)−1=0. We first prove the univalence of f(z) in U.To this end,we fix r with 0 We know from the proof of Theorem 3.1 that there is a unique ρ∈(0,1)satisfying eq.(3.1)such that for any two distinct points z,zin |z|<ρ,which proves the univalence of f in the disk U. Next,we consider any zwith |z|=ρ.By our proof of Theorem 3.1,we have By Lemma 2.4,we obtain that the range f(U) contains a schlicht disk U(w,r),where wand rare defined by (3.15). Now,we prove that the univalent radius ρis sharp.To this end,we consider the log-pharmonic mapping f(z)=e,where F(z) is given by (3.3).It is easy to verify that f(z)satisfies the hypothesis of Theorem 3.7,thus we obtain that f(z) is univalent in the disk U,and the range f(U) contains a univalent disk U(w,r). To prove that the univalent radius ρis sharp,we need to prove that f(z)is not univalent in Ufor each r ∈(ρ,1].In fact,if we fix r ∈(ρ,1],by our proof of Theorem 3.1,we know that F(z) is not univalent in U,thus there exist two distinct points z,z∈Usuch that F(z)=F(z),which implies that f(z)=e=e=f(z),that is,f(z) is not univalent in Ufor each r ∈(ρ,1].Hence,the univalent radius ρis sharp. Finally,we prove that the radius r=sinh σis sharp.In fact,by the proof of Theorem 3.1,we have that σ>0 and 0<ρ≤1/Λ.We now prove that σ<1. Figure 2 The image of an extremal function of Theorem 3.4 Remark 3.5 Setting p=1 in Theorem 3.4,we obtain the precise form of the Landau-Bloch type theorem of log-harmonic in U as follows: Remark 3.7 With the aid of Theorem 3.2 and Lemma 2.4,if we apply the same method as in our proof of Theorem 3.4,we obtain the following precise form of the Landau-Bloch type theorem for certain log-p-harmonic mappings(in particular,we obtain the accurate value of Bloch constant for certain log-p-harmonic mappings in U): (i) g(z) is log-harmonic in U,g(0)=1,and G:=log g; (ii) for each k ∈{2,···,p},Λ(z)≤Λ,and Λ(z)≤1 for all z ∈U. Then f(z) is univalent in U,where ρis given by (3.8).Moreover,the range f(U)contains a univalent disk U(w,r),where σis given by (3.10),and Both of the radii,ρand r=sinh σ,are sharp. Remark 3.9 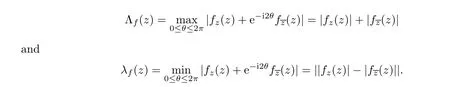
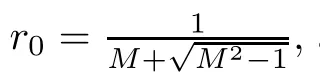
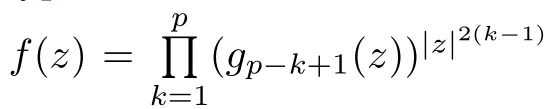

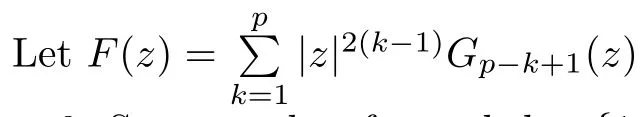
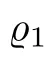
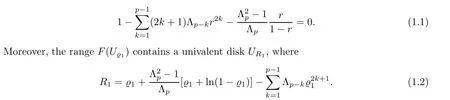
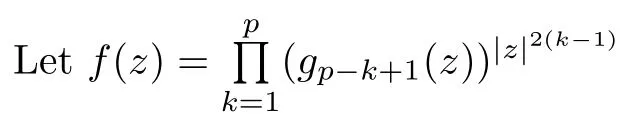
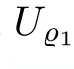
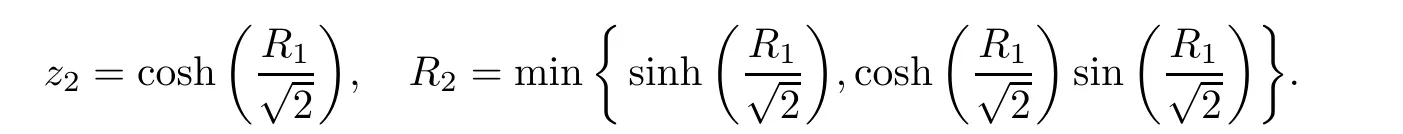
2 Preliminaries



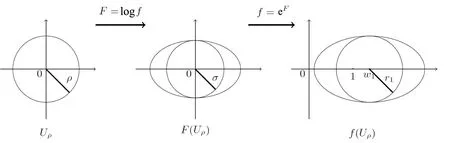

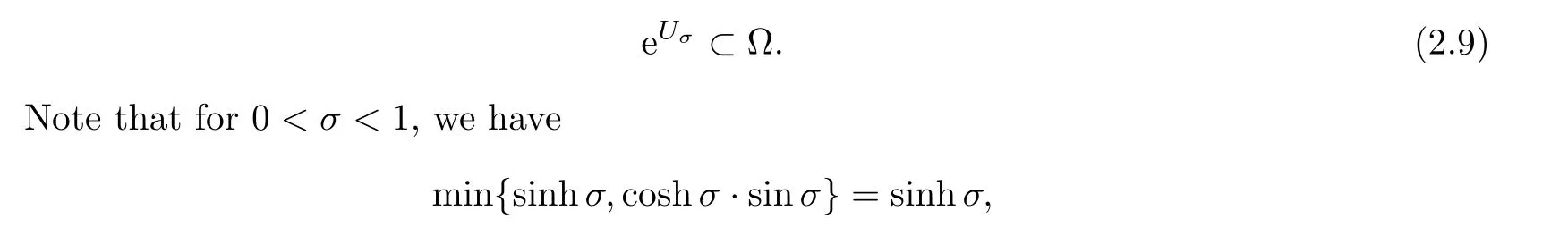

3 Main Results

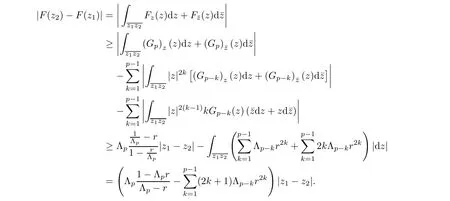
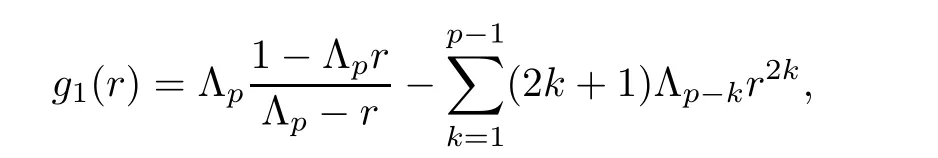
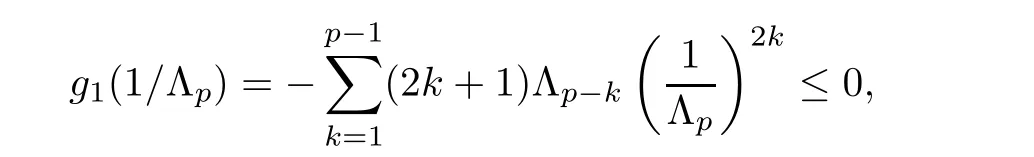
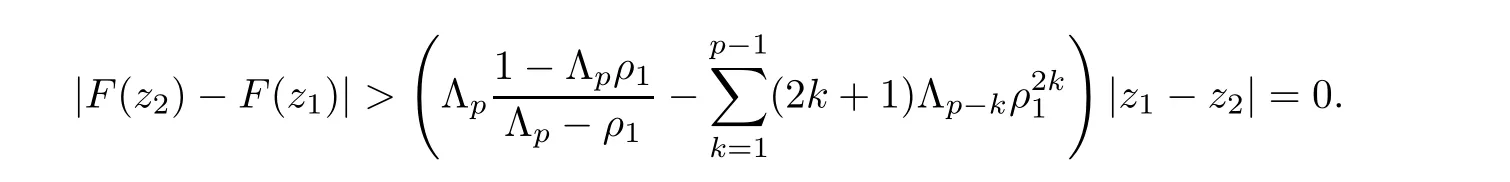
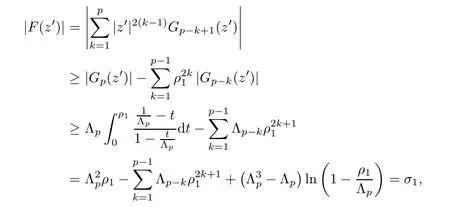
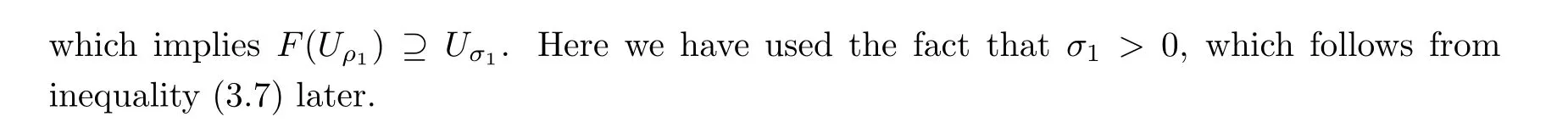

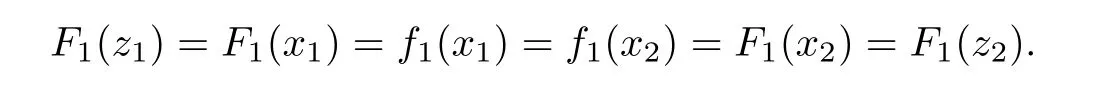
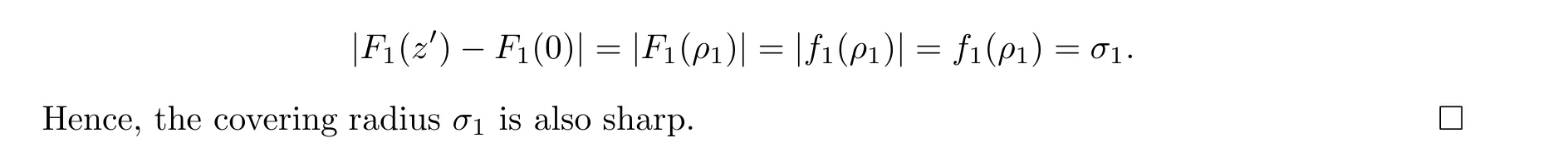
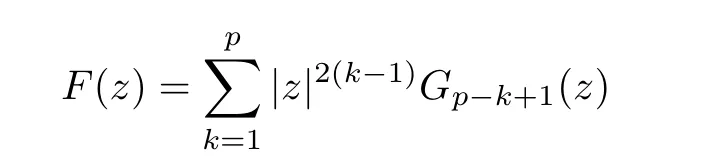
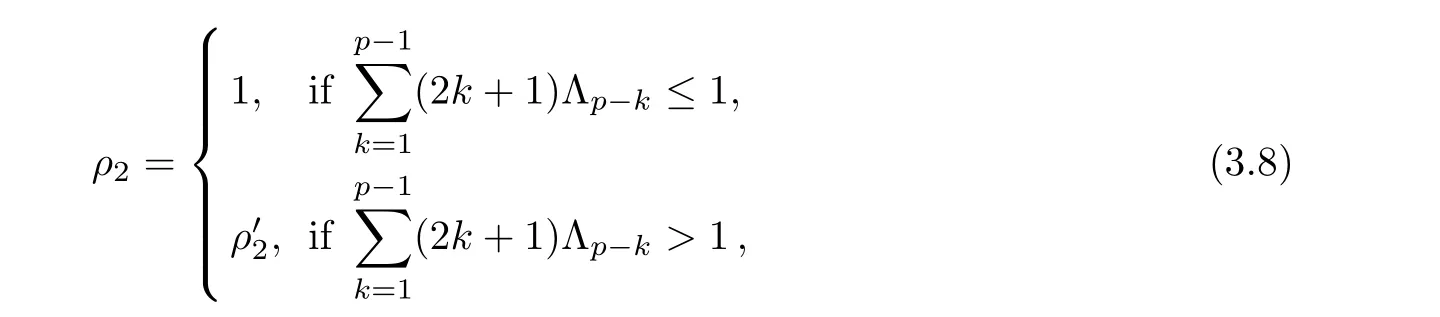
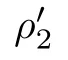

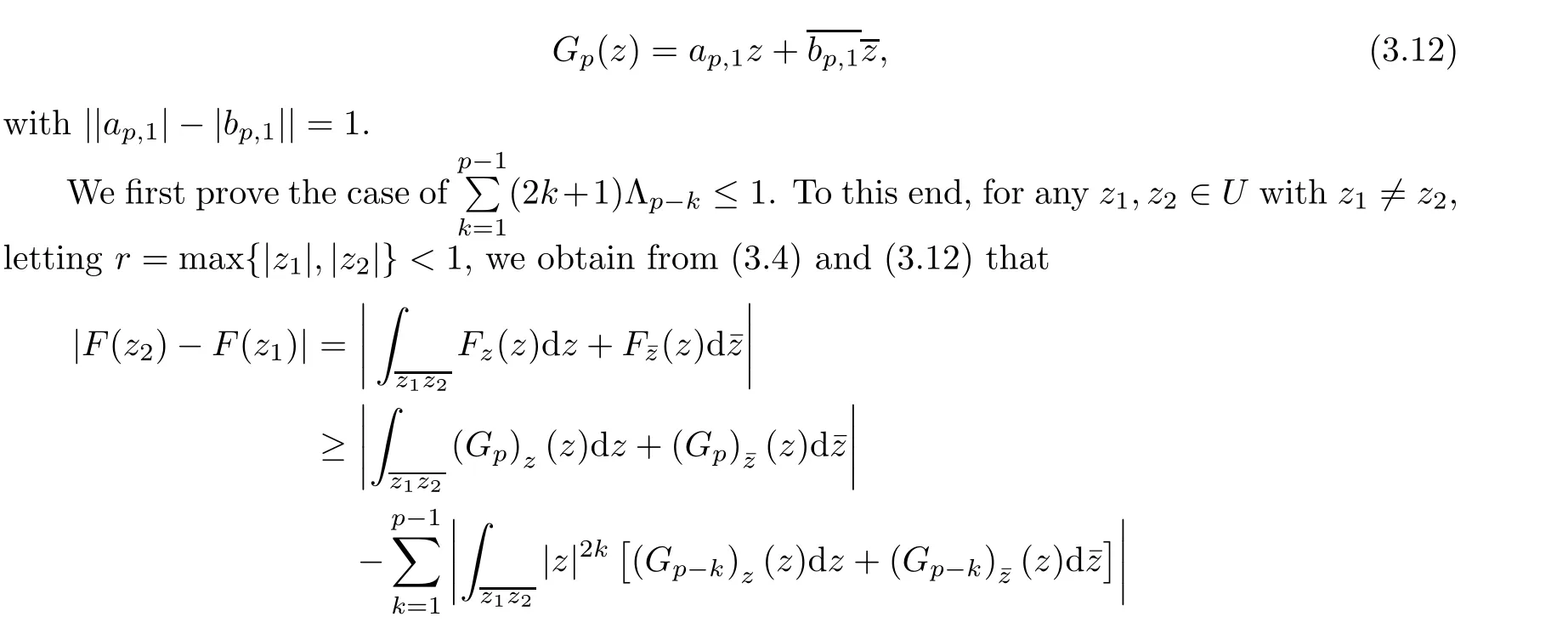

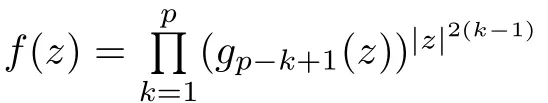

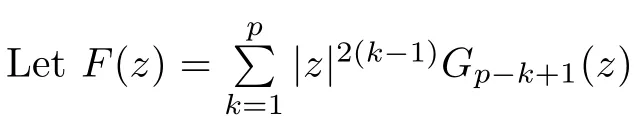
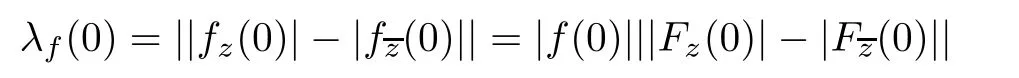
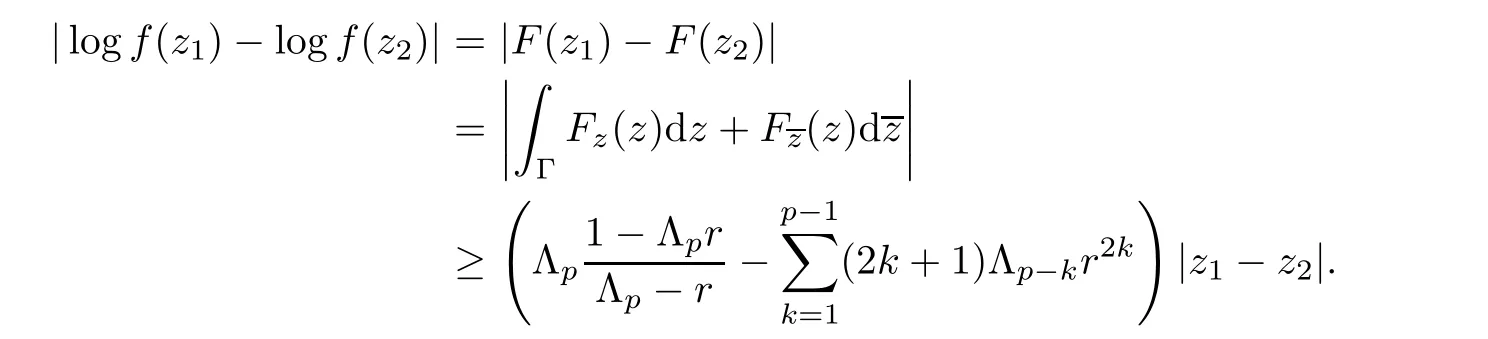
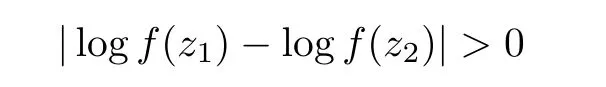



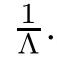
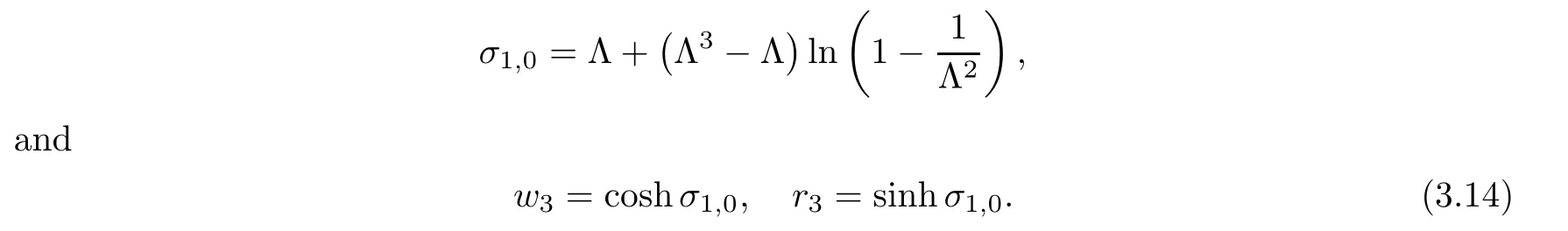


 Acta Mathematica Scientia(English Series)2021年1期
Acta Mathematica Scientia(English Series)2021年1期
