多源频率域地空系统三维电磁响应分析

张继锋， 刘寄仁， 冯兵*， 董岩， 郑一安

1 长安大学地质工程与测绘学院， 西安 710054 2 中南大学地球科学与信息物理学院， 长沙 410083

0 引言

传统的地面电磁法(包括可控源音频大地电磁法、瞬变电磁法等)是资源探查的重要手段，特别是在矿产资源及环境工程领域发挥了重要的作用(底青云等, 2019; Xue et al.，2020).随着“十三五”国家“四深”发展战略的提出，地球深部矿产资源的精细化探测提上日程，迫切需要发展新的技术方法.多道瞬变电磁法、广域电磁法、短偏移距瞬变电磁以及地空电磁法等一批新的探测技术应运而生(陈卫营等，2016；薛国强等，2020；Ji et al., 2016).地空电磁法融合了地面电磁法大功率发射和无人机空中快速非接触式采集的双重优点，能够进入地形复杂区域开展大深度资源勘探，近年来成为地球物理电磁法研究的热点(Allah et al., 2013, 2014; 李貅等, 2015；张莹莹和李貅，2017；Xue et al., 2018；Wu et al., 2019).该方法与无人机飞行平台相结合，有利于在中小区域开展大深度地下结构精细探测.相对于地面和航空电磁法，更加经济、安全和便捷，因此具有广阔的市场前景和应用价值.

地空电磁法的发展最早可追溯到20世纪70年代，加拿大TURAIR系统研制成功并用于安大略湖北部金属硫化矿的探测(Pemberton et al., 1970; Bosschart and Seigel, 1972).该系统采用地面大回线作为发射源，在近空区域测量特定频率下两个水平线圈或正交线圈的磁场比值以及相位差，发射功率可达15 kW，探测深度可达到200 m.90年代后期，一系列新的地空仪器设备相继出现，包括澳大利亚的FLAIRTEM系统，加拿大的TerraAir系统和日本GREATEM系统f621(Elliott,1998; Mogi et al., 1998 ).这几种设备采集方式都是观测一次场关断后瞬变电磁响应，解释仍然采用地面回线源的解释方法，只是前两种系统仍然采用大回线发射源激励，GREATEM系统采用地面电性源激励方式.进入21世纪，Smith等(2001)对地面、地空和航空瞬变电磁系统进行了对比研究，系统分析了三种方法的噪声水平和探测效果.结果表明：地空电磁系统的探测深度和数据质量均优于航空电磁系统，仅次于地面电磁系统.此后，电性源地空系统GREATEM先后用于火山区和海岸带地电结构探测，深度可达800 m，成为一种重要的深部电磁勘探方法(Mogi et al., 2009; Ito et al., 2011, 2014).德国BGR研究所(Nittinger et al.，2017)也推出了一套频率域地空电磁探测系统，并成功应用于金属矿探测中.目前地空电磁系统的研究主要以单辐射源为主，大量的研究集中在仪器研制和信号的去噪方面(嵇艳鞠等，2013；Wang et al., 2013；Qu et al., 2017; Li et al., 2017; 刘富波等，2017；Yuan et al., 2019).由于地空电磁法接收信号干扰较大，单源发射功率有限，探测深度和测量范围都会受到限制，因此，迫切需要发展地空多源电磁勘探系统和方法.

多源勘探概念最早应用在直流电阻率法中，Bibby(1986)提出多源测量模式并引入电阻率张量，该方法克服了视电阻率对目标体位置和方向的依赖，减少了单源测量结果的“假异常”现象，证明多源测量能够获得更可靠的信息.Caldwell和Bibby(1998)在长偏移距瞬变电磁(LOTEM)勘探中提出了多源瞬时电阻率张量，保留了直流电阻率张量的许多有用性质，特别是在地下三维电阻率分布情况下，许多解释技术可以应用于时间域电磁数据.90年代初，阻抗张量和倾子矢量被引入到地面可控源电磁测量中(Li and Pedersen,1991)，该方法一般采用两个相互垂直的激励源，分别从不同的方向激励，两个源单独工作，能够获取更加丰富的地电信息，解释结果更加可信，后来进一步得到发展(Caldwell et al., 2002).席振铢等(2011)研究了正交磁偶源电磁场分布规律，实现了可控源高频大地电磁张量测量；王显祥等(2014)等研究了“L”型源的各分量表达式，设计了一种新的信号发射模式，实现了全张角范围内测量，显示了张量可控源方法的优势.

近年来，多源地空电磁系统的研究也逐渐受到了重视，李貅等(2015)提出了多辐射场源的全域视电阻率定义方式，不仅提供了一种定性直观的解释方法，也为三维多源地空瞬变电磁的发展提供了理论依据.Zhou等(2018a，b)年提出频率域多源电磁探测方法，主要从仪器的研制、激励信号的同步以及多源之间的相互影响等方面进行了研究，表明多源地空电磁勘探具有广阔的发展前景.因此，需要进一步从三维角度对多源电磁响应进行模拟和分析.目前地球物理电磁法三维数值模拟主要集中在单激励源或被动源三维模拟方面(李建慧等, 2016; Ren et al., 2013, 2014; 殷长春等, 2017)，多源频率域地空三维电磁响应特征研究比较少，特别是全域视电阻率分布特征和规律.

本文采用多源三维有限元数值模拟方法，从多源辐射角度出发，设置了双源、三源以及四源辐射方式，建立了低阻体、高阻体模型以及两个低阻体模型，分别从总场、二次场以及视电阻率参数等方面对不同发射源模式进行分析，总结每种源的电磁响应和全域视电阻率特征，为实际选择多源辐射方式进行地空电磁勘探提供理论基础.

1 多源频率域地空系统

地空频率域电磁探测方法是采用地面布设发射源，空中测量垂直磁场响应的工作模式.该方法由吉林大学教授林君提出，其仪器(GAFEM)已经研制成功，采用伪随机发射波形，在一些老矿区进行了野外试验，取得了良好效果.单辐射源能量有限，信号强度弱，加之受运动噪声的影响，信噪比和探测深度都会受到一定的影响.多场源激励可改变空间磁场分布，提高信号强度，扩大观测区域，提高信噪比.通过多场源不同角度和不同方向激励，可加强发射源与目标体的耦合程度，改善对目标体的分辨率(图1).频率域地空电磁法测量空中磁场垂直分量，不再测量电场分量，场的特征和解释方法完全不同，地面的处理解释方法不再适用.因此，必须基于空中磁场分量，研究三维地电模型的电磁场空间分布特征和新的解释方法.

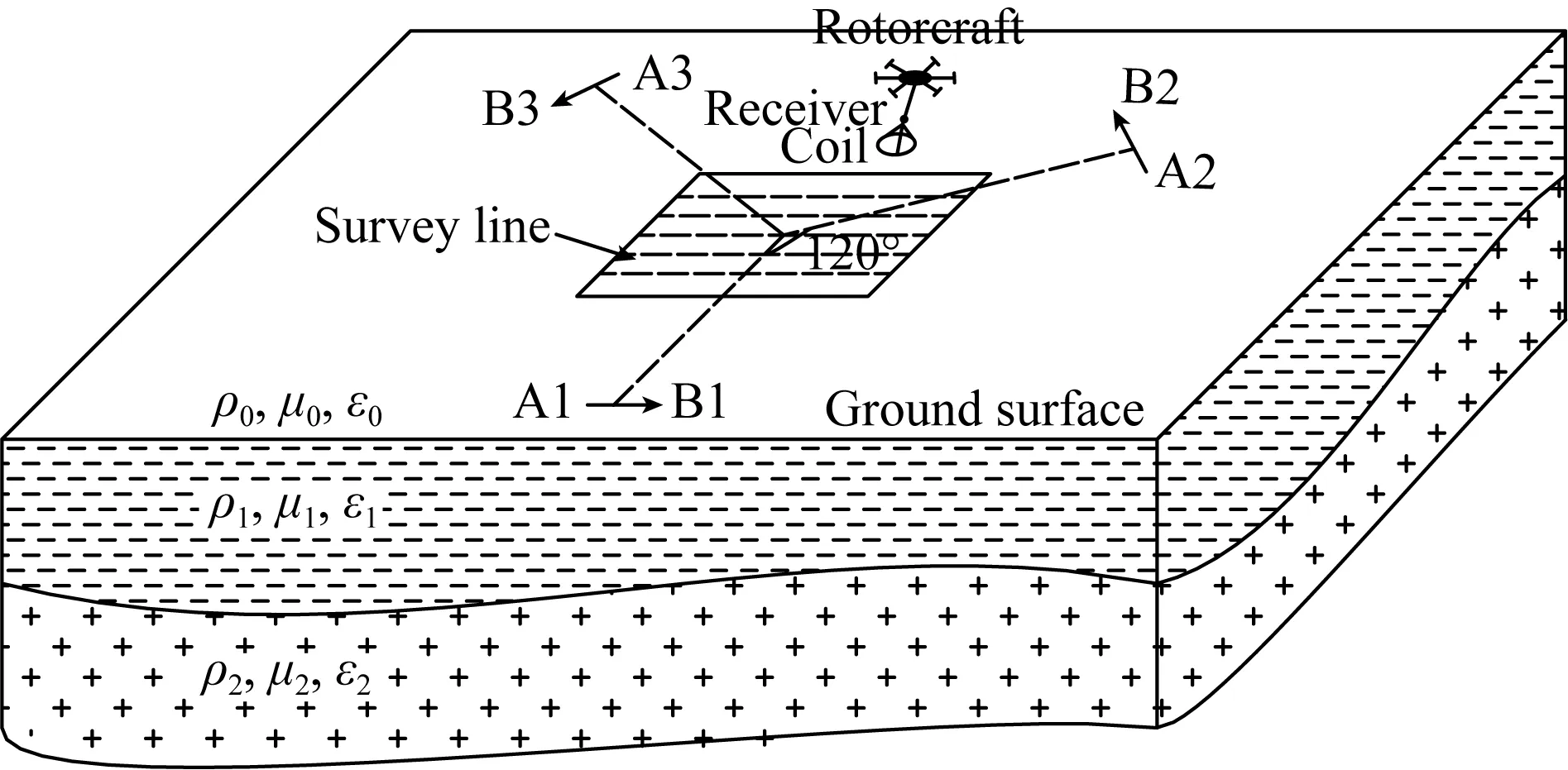
图1 频率域多源地空电磁采集方式示意图Fig.1 Schematic diagram showing data acquisition for multiple-source frequency domain grounded-airborne electromagnetics

2 多源频率域地空有限元分析

2.1 基于总场的公式

在准静态极限条件下的电场E和磁场H所满足的频率域方程为(汤井田和何继善，2005):

(1)

(2)

其中假设电磁波的谐变因子为eiω t，式中μ为磁导率，本文μ选取真空磁导率μ0，σ为电导率，ω为圆频率，Js为传导电流密度.

由此便可导出电场双旋度方程：

(3)

(4)

其中，V为研究区域的体积，在进行节点有限元求解时，该方程不满足散度条件，产生的伪解直接影响计算精度.为了提高计算精度，可在方程中增加一个罚项来削弱伪解产生的影响(金建铭，1998)：

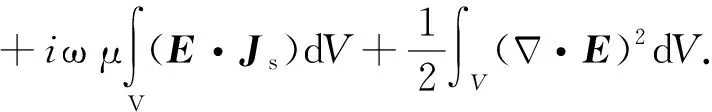
(5)

2.2 有限元分析

本文采用非结构化网格剖分方法，利用TetGen生成高质量的四面体网格，将源和异常体附近场值变化剧烈的区域进行网格加密，网格边界大于10倍的趋肤深度，以保证场值在边界上已衰减为零，如图2所示.

图2 非结构化网格剖分Fig.2 Unstructured grid

图3 四面体单元Fig.3 Tetrahedron element

(6)

若将整个研究区域剖分为n个单元，离散化后的变分方程为：

(7)

那么地空多源正演问题转化为求解该变分方程的极值问题，该方程可看成多元函数，多元函数取极值应当满足下列方程(徐世浙，1994):

(8)

其中i为节点编号，e为单元编号.

由此可得到所有单元所满足的矩阵方程：

(9)

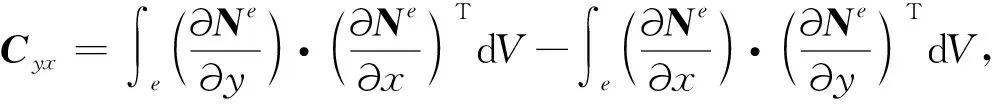
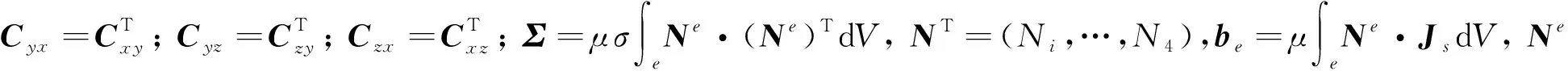
按照单元节点的编号，可将每个单元生成的子矩阵组合成总体刚度矩阵，得到最终的离散矩阵方程：

(C+iωM)·E=-iωb.

(10)

由于产生的刚度矩阵是大型的对称稀疏矩阵，直接存储将会浪费大量存储空间，因此本文采用双向链表组装矩阵，按CSR方式存储.由于多频可控源正演模拟的频点之间是相互独立的，解方程将会浪费大量的时间，严重影响运算效率，而经前人研究发现，可以通过模型降阶方法，将一个复杂的系统简化，只要经过一次模型降阶，便可实现多频点的计算，提高运算速率(蒋耀林，2010；Börner et al., 2008；周建美等，2018).

2.3 模型降阶方法

对于矩阵方程(10)，我们可以做如下变形：

(M-1C+iωI)·E=-iωM-1b，

(11)

令A=M-1C，X=M-1b，gω(A)=-iω(A+iωI)-1，解得E(ω)=-iω(A+iωI)-1X=gω(A)X.那么求解E(ω)的关键便是求解gω(A)，因此我们采用Krylov子空间(张继锋等，2009, 2020)投影算法，可降低矩阵运算的维数，大大提高运算效率.

模型降阶算法实际上就是寻找一个有效逼近rm(A)，使得E≈rm(A)成立，求解rm(A)等价于求解矩阵A在m维Krylov子空间Qm+1=qm(A)-1κm+1(A,X)上的投影(周建美等，2018).由于有限元离散矩阵的特点，矩阵M并非单位矩阵，为了避免因传统正交算法造成运算的复杂性，我们引入一种M正交运算(蒋耀林，2010; Börner, et al., 2015)，进而得到列正交向量Vm+1，下面给出模型降阶后的最终表达式：

E=‖X‖MVm+1gω(Am+1)e1，

(12)

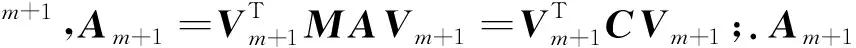
2.4 垂直磁场的求取

求解方程(10)可得到整个区域所有节点的电场三分量值，而在任意单元e中，任意点(x0,y0,z0)处的电场大小可通过插值基函数求得：

(13)

在地空系统中，电偶源在地面发射电流，线圈在空中接收磁场，因此本文通过研究z方向的磁场值Hz来研究大地的电性特征.由式(1)可得：

(14)

其中相应场在某一点的导数值可通过式(13)代入式(14)求得.在实际数据处理和资料解释中，为了能够直观的反映地下介质的电性特征，我们需要将磁场转化为视电阻率.张莹莹等(2015)定义了时间域瞬变电磁场的全域视电阻率，我们将其引入到频率域，利用泰勒级数展开，求得视电阻率的近似表达式，然后通过迭代算法得到全域视电阻率.

3 多源三维电磁响应分析

3.1 有限元解和解析解的比较

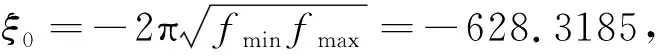
图4a、b分别给出了有限元解和解析解的垂直磁场分量以及相对误差.可以看出，三维有限元计算结果同一维正演结果吻合的很好，磁场最大误差为1.8%左右.

为了进一步验证程序的正确性，我们设计了一个两层模型，第一层电阻率为200 Ωm，厚度为100 m，第二层电阻率为50 Ωm.第一个源沿x轴正方向放置，电偶源的中心位置为(0 m，-4000 m，0 m)，第二个源沿x轴负方向放置，电偶源的中心坐标为(0 m，2000 m，0 m)，设置测点位置为(1600 m，-2000 m，-100 m).如图5所示，磁场相对误差最大不超过3%，说明基于模型降阶的有限元计算结果满足精度要求.

3.2 三维电磁响应分析

3.2.1 低阻体模型

(1)单源和多源比较

为了说明频率域多源地空电磁方法的优势，设计一个低阻体模型，针对垂直磁场分量,比较几种多源组合模式的电磁场分布.低阻体模型如图6所示，异常体电阻率为10 Ωm，大小为500 m×500 m×300 m，异常体中心坐标为(0 m，0 m，250 m), 围岩电阻率为100 Ωm.图6c为非结构化网格剖分图.为便于对比多源组合方式，假设所有的电性源偶极矩为1000 Am，飞行高度30 m.

图4 均匀半空间3D-Forward、1D-Forward的磁场Hz及对应的误差曲线(a) 磁场Hz； (b) 相对误差曲线.Fig.4 Magnetic field Hz and relative error for homogenous half space from 3D- and 1D-forward modeling(a) Magnetic field Hz; (b) Relative error.

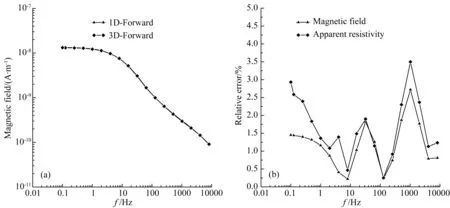
图5 两层模型3D-Forward与1D-Forward的磁场Hz及对应的误差曲线(a) 磁场Hz； (b) 相对误差.Fig.5 Magnetic field Hz and relative error of two-layer model from 3D- and 1D-forward modeling(a) Magnetic field Hz； (b) Relative error.

图7为多个源的位置示意图，我们分析几种组合方式：①单源，①②组合，①③组合，①②③组合，①②③④组合，①⑤⑥组合.各个源的中心坐标已在图7中给出.

我们首先给出256 Hz各种组合源作用下的均匀半空间电磁响应.图8为各种组合源作用下的垂直磁场切片图，可以看出，靠近源的一侧磁场强，而远离源的一侧磁场逐渐衰减，同时我们也注意到，这几种组合源都将使得背景场值增大，信号强度增强，这是多源场之间的相互叠加作用导致的.图9给出了中心测线全域视电阻率测深曲线及相对误差，可以看出,全域视电阻率基本接近于背景电阻率100 Ωm，误差不超过2.5%，完全满足计算精度要求，也说明本文全域视电阻率算法的正确性.

图10给出了单源和多源作用下，含异常体的总场幅值分布切片图，图11为相应的二次场分布图，图12是单源和多源情况下异常幅度的分布图，图13给出了单源及多源作用下的全域视电阻率分布图.从中可以看出，若在单源作用下测量垂直磁场时，在靠近源的一侧和远离源的一侧由于在界面上电阻率突变，导致界面产生积累电荷，磁场响应增强，异常体的中心与异常响应的极值并不对应，在靠近源的一侧边界将会使得场值增大，而在远离源的一侧边界将会使场值减小，如图10a和图11a所示，而磁场增大将会使得全域视电阻率增大，因而在靠近源的一侧边界处出现出高阻极大值，而在远离源的一侧边界处出现了低阻极小值，如图13a所示.可见，对于三维地电模型的电磁响应分布比较复杂，异常体的位置和磁场及全域视电阻率形态并不一定吻合，需要进行仔细分辨.磁场分布不仅与异常体的形态有关，也与异常体与源的相对位置有很大关系.

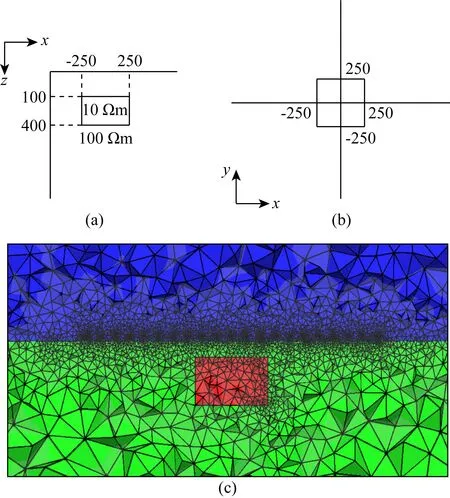
图6 低阻体模型(a) 剖面图； (b) 平面图； (c) 非结构化网格剖分图.红色代表低阻体，绿色代表背景.Fig.6 Model of a conductive body(a) Cross-section； (b) Plane view； (c) Unstructured grid.Red shows the conductive body and green shows background.

分析①②组合源和①②③组合源的电磁响应，发现总场和二次场的幅度都在一定程度上有所增强，如图10b、图10d、图11b、图11d所示.这也是多源的优势之一，可增强观测区域的信号强度.为了更好的反映异常响应分布，需要分析其异常响应的相对幅值，如图12b、d所示，我们发现在边缘处的极大极小值的相对幅度在减小，这是不同方向上的源产生的场在边界区域进行叠加的结果，导致异常场的分布形态发生了变化，而图13b、d视电阻率分布图也说明了这一点，在边缘处的电阻率极大值在减小，而极小值在增大.图10c、图11c是①③组合的总场幅值和二次场大小，这与单源情况下相比，也提高了信号强度，而从相对幅度分布图12c及全域视电阻率图13c来看，在异常体的中心出现了低阻圈闭，在边缘部位出现了高阻响应.这种源的组合方式在异常形态分布上优于前面分析的三种方式，能更好的反映异常的中心位置，削弱了异常体边界处的假极值，但是在源的方向上，出现了拉长的低阻，而在垂直源的方向上出现了高阻.

图8 256 Hz单源和多源的垂直磁场分布图(a) ①； (b) ①②； (c) ①③； (d) ①②③； (e) ①②③④； (f) ①⑤⑥.Fig.8 Vertical magnetic field of single and multiple sources at 256 Hz

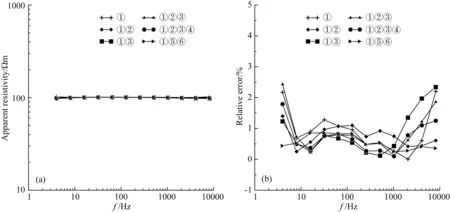
图9 中心测点全域视电阻率及相对误差(a) 全域视电阻率； (b) 相对误差.Fig.9 Full-domain apparent resistivity and relative error curves of central measuring point(a) Full-domain apparent resistivity; (b) Relative error.

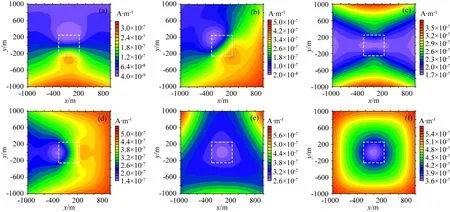
图10 256 Hz单源和多源的总场幅值分布图(a) ①； (b) ①②； (c) ①③； (d) ①②③； (e) ①②③④； (f) ①⑤⑥.Fig.10 Total magnetic field Hs at 256 Hz of single and multiple sources

图11 256 Hz单源和多源的二次场响应分布图(a) ①； (b) ①②； (c) ①③； (d) ①②③； (e) ①②③④； (f) ①⑤⑥.Fig.11 Secondary magnetic field at 256 Hz of single and multiple sources

图12 256 Hz单源和多源的异常相对幅度分布图(a) ①； (b) ①②； (c) ①③； (d) ①②③； (e) ①②③④； (f) ①⑤⑥.Fig.12 Relative percentage of anomaly at 256 Hz of single and multiple sources

图13 256 Hz单源和多源的全域视电阻率分布图(a) ①； (b) ①②； (c) ①③； (d) ①②③； (e) ①②③④； (f) ①⑤⑥.Fig.13 Full-domain apparent resistivity at 256 Hz of single and multiple sources

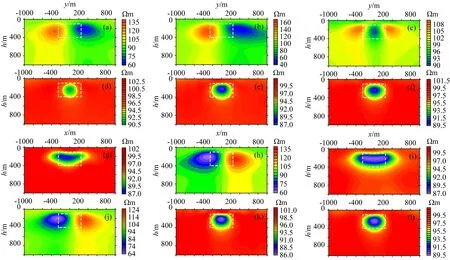
图14 单源和多源的主轴剖面的广域视电阻率图(a)、(g) ①； (b)、(h) ①②； (c)、(i) ①③； (d)、(j) ①②③； (e)、(k) ①②③④； (f)、(l) ①⑤⑥.Fig.14 Full-domain apparent resistivity of single-source and multiple sources spindle sections

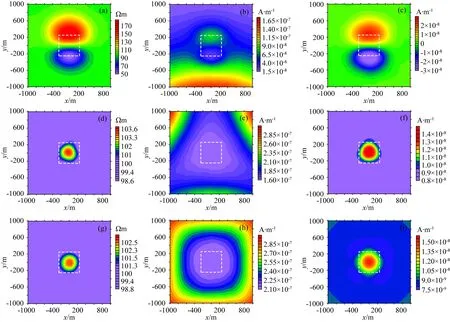
图15 256 Hz单源和多源全域视电阻率、总场幅值和二次场响应(a)—(c) ①； (d)—(f) ①②③④； (g)—(i) ①⑤⑥.Fig.15 Full-domain apparent resistivity, total field and secondary filed responses at 256 Hz of single and multiple sources

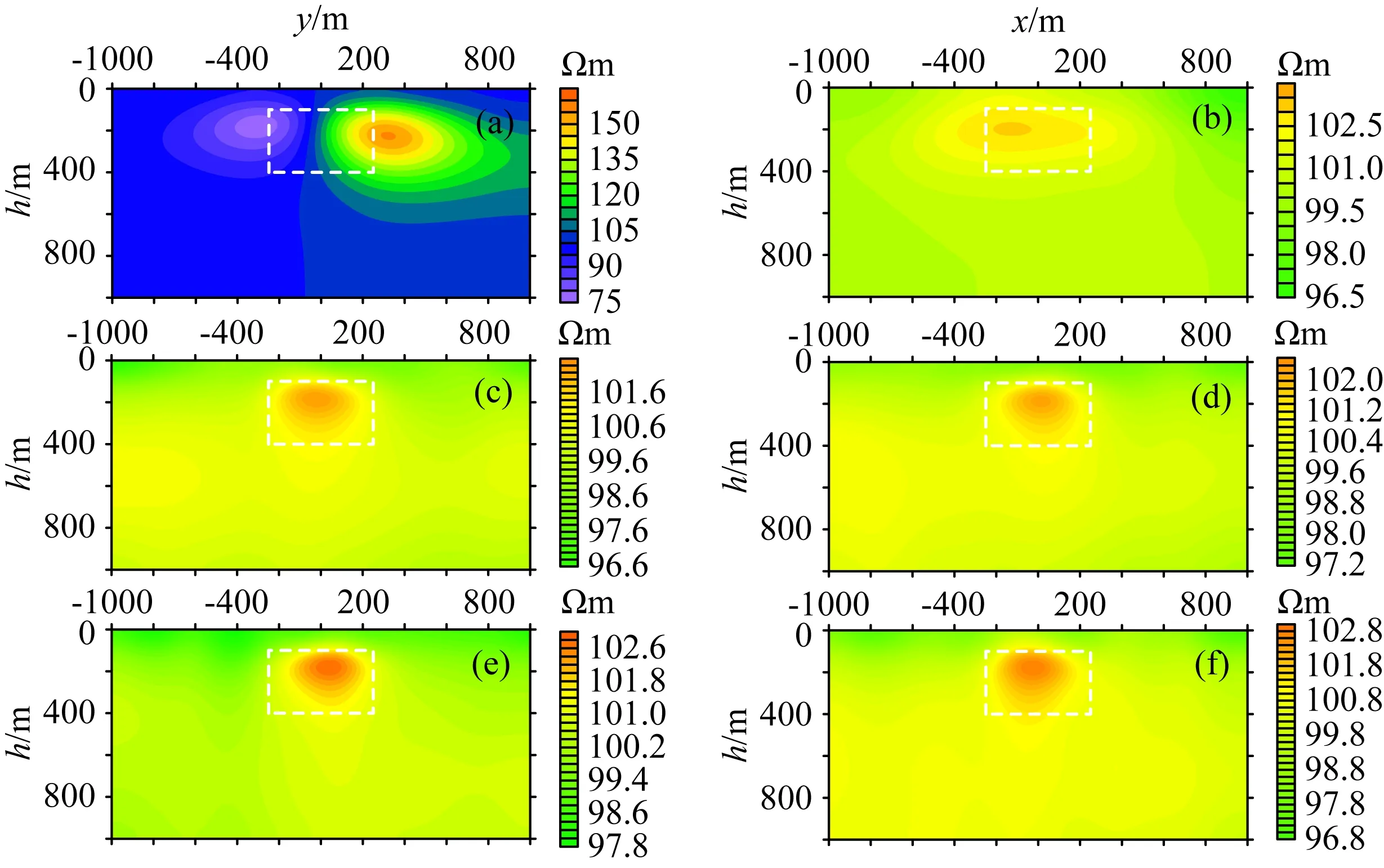
图16 单源和多源的主轴剖面的广域视电阻率图(a)、(b) ①； (c)、(d) ①②③④； (e)、(f) ①⑤⑥.Fig.16 Full-domain apparent resistivity of spindle sections of single source and multiple sources

从①③组合方式来看，当源关于异常体的中心出现对称分布时，对异常体的分辨较好，因而本文还设计了①②③④组合和①⑤⑥组合，而①⑤⑥组合三个源相互呈120°对称，从总场幅值和二次场分布可看出，在测网中心出现了低阻圈闭，且①②③④组合的总场极小值比其余组合方式的极小值更大，说明①②③④组合在增强信号强度方面是最强的，而在二次场分布方面，由于场源和异常体的对称性，这两种方式基本消除了异常体边界的极值，突出了异常中心的电性特征，而异常相对幅度和全域视电阻率分布更好的说明了这一点，在没有异常体的区域，受到异常体的影响很小，几乎接近于背景值，而在异常体中心形成了很明显的低阻异常圈闭，因而这两种方式都能够提高磁场的信号强度，同时使全域视电阻率分布形态更接近于真实的地电分布.若不考虑其他因素，①②③④组合是相对较优的多源组合方式，若考虑野外施工效率，也可选择①⑤⑥多源组合方式.

接下来我们分析每个组合方式的主测线剖面图，包括x=0测线和y=0测线，如图14所示，图14a—f表示单源和多源组合的x=0测线剖面，图14g—l表示单源和多源组合的y=0测线剖面.从中可看出，单源激励下，两条测线仅平行于源的测线出现了低阻圈闭，另一条垂直测线靠近源的一侧呈现高阻，远离源的一侧呈现低阻，这和上述切片图是一致的(图14a、 g).组合源①②的两条测线均没有在异常体位置出现低阻圈闭.对于①③组合，在切片图中已展现出较宽的低阻圈闭，而两条中心测线的剖面图也能较好的体现异常体的位置，但平行源的测线低阻圈闭横向范围宽(图14i)，而其x=0测线在边界处呈现了高阻响应，中心低阻圈闭较小(图14c).①②③组合的切片图形与单源形式是类似的，因而其剖面图的形态也类似，只是出现低阻圈闭的测线相反.①②③④组合和①⑤⑥组合的两条中心测线都出现了明显的低阻圈闭，而且与异常体的位置对应的较好，周围围岩呈现出背景电阻率，这两种组合更容易识别异常体的分布.

3.2.2 高阻体模型

同样，我们也分析了高阻体的地空三维电磁响应分布，图15a—c为单源作用下的高阻异常体响应，可以看出在靠近源的一侧表现出了低阻性质，而在远离源的一侧表现出了高阻性质，这与低阻体的响应是相反的.从①⑤⑥组合和①②③④组合的响应来看，异常响应呈现高阻圈闭，消除了边缘的假极值.而图16给出了相应的主轴剖面，从中看出，单源情况下的x=0测线剖面和y=0测线剖面的形态和低阻体单源情况下的剖面形态是一致的，只是高阻和低阻发生了倒转，如图16a、b所示，也可以看出，y=0测线的高阻圈闭形态出现误差，这是因为地空响应对高阻体不敏感造成的，产生的异常响应和围岩的电阻率较为接近，因而对高阻体的灵敏度不如低阻体.从①②③④组合和①⑤⑥组合的中心测线剖面可以看出，每种组合的两条中心测线都出现了高阻圈闭，虽然异常幅度较低，但是能够很好的反映异常体的位置.

3.2.3 两个低阻体模型

建立两个大小相同的低阻体，大小均为400 m×500 m×300 m，电阻率都为10 Ωm，关于y轴对称，左边异常体中心为(-400 m，0 m，250 m),右侧异常体中心为(400 m，0 m，250 m)，背景电阻率为100 Ωm，图17a为模型剖面图，图17b为模型平面图，图17c为源的位置示意图，图17d为非结构化网格剖分图.

共设计了三种场源的组合方式，在单源①的作用下，靠近源的一侧呈现两个了高阻，而远离源的一侧呈现了两个低阻圈闭，且对称分布，如图18a—c所示，这与前文的结果是吻合的.而①⑤⑥组合和①②③④组合的响应也呈对称分布，但是较单源而言，低阻异常的位置同实际位置更加接近，两侧呈对称分布的高阻异常也已大致趋于背景值，而异常响应在两个低阻体相互靠近的一侧边缘出现了低阻极小值，虽然和异常体并没有完全吻合，但比单源作用下的响应形态更简单，更能反映异常体的电性分布特征.

为了更好的比较，我们给出了不同频率下两条中心测线(x=0和y=0)的垂直磁场变化曲线,如在图19, 可以发现，在y=0测线上，多源激发下垂直磁场都出现了两个低值凹陷，但明显四源和三源情况下的凹陷位置更接近于异常体的中心，而单源激发下，在中间位置磁场响应却增大了，与实际模型电性不一致(图19e).从剖面图整体上可以看出，多源的信号强度明显强于单源的信号，这对于实际测量非常有利，在相同噪声背景下能够提高信噪比，如图19a、c、e所示.而对于x=0测线，四源和三源在中心位置出现了低阻凹陷，单源在中心位置两侧则出现了一个突起和一个凹陷，这个与平面图的异常特征一致，多源激励不仅可以增强信号的强度，而且可以改变目标体的异常响应特征，如图19b、d、f所示.

为了方便说明，在图20中给出了512 Hz的中心测线(x=0和y=0)全域视电阻率变化曲线，对于y=0测线，四源和三源均出现了两个低阻凹陷，且刚好对应异常体的中心位置，而单源在异常体边缘处出现了极小值，中间位置则出现了极大值(图20a).而对于x=0测线，四源和三源情况下均出现了低阻凹陷，这是因为虽然测线没有经过异常体，但旁侧两个低阻异常体在多源激励下出现视电阻率低值，而单源激励下两侧分别出现了较强的极大极小值分布，不利于异常体电性特征及平面位置的定性分析(图20b).

4 结论

本文采用基于电场双旋度方程的非结构化节点有限元方法，成功实现了多源地空电磁响应特征的模拟和分析.通过Krylov子空间模型降阶技术大大降低了大型稀疏矩阵的维度，然后直接求逆矩阵便可得到传递函数，进而求得多频电磁方程的解.采用均匀半空间和层状模型，通过和一维解析解进行对比，验证了本文算法的正确性和有效性.通过泰勒级数展开取线性主部的迭代算法计算多源激励的全域视电阻率，并将其应用于三维地下介质的定性分析解释.三维地电模型的多源电磁响应分析表明：对于单个常体，一般单源激励会在靠近源的一侧出现高视电阻率，远离源的一侧出现低视电阻率；而对称的三源或四源激励模式可削弱场在边界上的响应，其全域视电阻率特征相对简单，和地下介质电性分布较吻合，这对于寻找浅地表独立的目标体，如未爆炸的炮弹、地雷等是有利的.对于邻近两个低阻异常体，多源激励模式不仅能够增加信号的强度，而且能够提高横向分辨率.实际地下介质的电性变化非常复杂，多源激励的电磁响应及全域视电阻率可为定性解释提供参考，精细化的解释将进一步依赖于地空三维电磁反演方法的发展.

图17 模型示意图(a) 剖面图； (b) 平面图； (c) 源的加载方式； (d) 网格剖分. 红色代表低阻体，绿色代表背景.Fig.17 Model of two conductive bodies(a) Cross-section； (b) Plane view； (c) Loading manner of source； (d) Unstructured grid. Red shows the conductive body and green shows background.

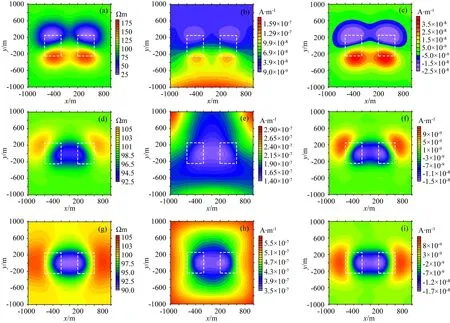
图18 256 Hz两个低阻体的单源和多源全域视电阻率、总场幅值和二次场响应(a)—(c)①; (d)—(f)①⑤⑥; (g)—(i)①②③④.Fig.18 Full-domain apparent resistivity, total and secondary vertical magnetic field at 256 Hz of single and multiple sources

附录A

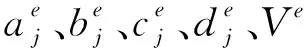
(A1)

(A2)

(A3)

(A4)

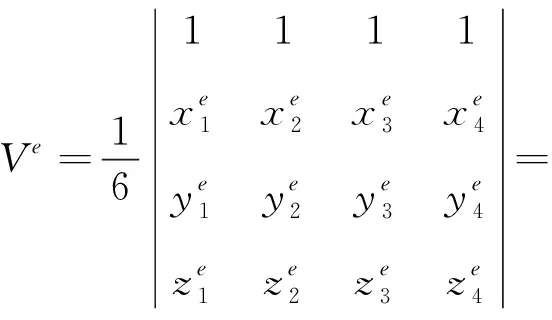
(A5)

图19 不同频率两条中心测线的垂直磁场变化曲线图(a)、(b) ①②③④； (c)、(d) ①⑤⑥； (e)、(f) ①.Fig.19 Vertical magnetic field curves of different frequencies in two central survey lines

图20 512 Hz下中心测线的全域视电阻率曲线(a) y=0； (b) x=0.Fig.20 Full-domain apparent resistivity curves at 512 Hz