基于交叉梯度结构约束的大地电磁主轴各向异性并行三维反演
王堃鹏, 王绪本, 曹辉, 蓝星, 段长生, 罗威, 原健龙
1 成都理工大学地球物理学院, 成都 610059 2 油气藏地质及开发工程国家重点实验室(成都理工大学), 成都 610059 3 中国地质调查局成都地质调查中心, 成都 610081 4 四川省冶勘设计集团有限公司, 成都 610051 5 赣中南地质矿产勘查研究院, 南昌 330029
0 引言
大地电磁(MT)是目前广泛使用的一类重要电磁勘探方法,被广泛应用于油气矿产勘探及地球动力学领域的研究(Zhang et al.,2014;Heinson et al.,2006;王绪本等,2013).然而地下介质电性各向异性的客观存在,以及它对MT观测数据的影响,使其受到越来越多的关注(Wannamaker,2005;刘云鹤等,2018).许多学者从正演出发,不断的研究它对MT观测数据的影响规律.Pek和Verner(1997)使用有限差分法研究了二维MT的各向异性正演. Li和Pek(2008)利用自适应有限单元法实现了一般各向异性的MT二维正演.Kirkby等(2015)尝试使用各向异性正演研究断裂分布. 嵇艳鞠等(2016)实现了一种基于无网格法的各向异性正演.曹晓月等(2018)研究了考虑地形的自适应各向异性正演.王宇等(2019)使用有限体积法研究了MT二维各向异性.Guo等(2018)实现了模块化的各向异性MT二维正演.Xiao等(2018)利用有限单元法研究了MT三维各向异性.基于这些学者大量的研究,MT观测数据受电性各向异性影响的规律正在被逐渐认识,尤其是对地质解释可能造成的干扰已经受到了广泛关注.
同时,一些学者尝试在MT反演中直接反演电性各向异性参数.Yin(2003)与Pek和Santos(2006)在一维介质模型中加入了各向异性参数反演.Schmoldt和Jones(2013)研究了一种新的二维MT各向异性反演方法.Montahaei和Oskooi(2014)使用神经网络法实现了MT二维各向异性反演,并对南美洲多条MT测线的实测数据进行了各向同性与各向异性反演研究与分析.Martí(2014)总结了关于MT各向异性的正演和反演研究现状.Cao等(2018)实现了MT三维主轴各向异性反演.Johansen等(2019)利用MARE2DEM(Key,2016)对一条海底测线数据实施了CSEM (Controlled-Source Electromagnetic Method,可控源电磁法)与MT的主轴各向异性二维反演.上述研究在考虑各向异性参数时,并没有充分研究结构约束对MT各向异性反演的影响.
加入各向异性参数的反演,从理论而言可以进一步减少各向同性反演产生的假异常,但受限于观测数据的不足,实际上可能加剧多参数反演的不确定性.因此,直接反演各向异性介质的所有参数非常困难.现有的常规思路首先是简化各向异性介质,比如VTI (Vertical Transversely Isotropy,垂直对称轴的横向各向同性)介质、主轴各向异性介质等(罗鸣等,2016;Key,2016;彭荣华等,2019).除此之外,为了进一步缩小模型空间,还可以在各向异性反演中强加对各向异性参数的约束.Pain等(2003)提出了一种各向异性罚函数来约束各向异性反演.Meju等(2018,2019)使用交叉梯度法,对海洋可控源电磁法三维各向异性反演实施了进一步的结构约束.
根据上述研究现状,我们将在已有的三维MT各向异性反演基础上(Cao et al.,2018),选用交叉梯度项对各向异性参数进行结构约束,用于约束的结构信息可以来自人工地震、天然地震或重磁等方法.本文的正演将大地电磁场分为一次场和二次场,并将各向异性介质简化为仅考虑X、Y、Z方向电阻率的主轴各向异性,简化后的X、Y、Z三个方向电阻率可以自由的受输入结构的约束,本文的结构约束方案同样能用于联合反演,不仅局限于实现结构约束.
1 基于二次场的MT主轴各向异性三维正演
本文将大地电磁三维正演进行背景场和二次场分解,取时谐因子为e-iω t,且忽略位移电流,可得到如下关于电场的似稳态偏微分方程:
(1)
(2)
其中,ω为圆频率,μ0为真空磁导率,σ为介质电导率,Js表示源项.将(1)、(2)式做简单代换,可得到电场的二阶偏微分方程:
(3)
将(3)式减去背景场,可获得二次场的二阶偏微分方程:
(4)
式中σp为背景电导率,Ep为背景电场.这里的背景电场利用一维层状介质的大地电磁方程计算获得.为了降低各向异性反演的多解性和不稳定性,本文将(4)式中的电导率参数σ替换为如下主轴各向异性参数:
(5)
则(4)式在三个方向的微分方程如下:
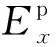
(6)
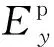
(7)
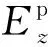
(8)
针对(6)—(8)三式,本文采用Yee格式及交错网格有限差分法进行离散,最终的方程采用QMR (Quasi Minimal Residual,拟最小残差)算法求解.关于主轴各向异性三维正演的更多细节可参考作者已发表的论文(Cao et al., 2018),本节不再赘述.
2 基于交叉梯度约束的MT三维主轴各向异性反演
2.1 各向异性目标函数
本文采用LBFGS法进行反演迭代计算,由于存在三个方向的参数并且观测数据为复数阻抗,本文设目标函数为:
φ=φd+λxφm_x+λyφm_y+λzφm_z+λcgxφcgx
+λcgyφcgy+λcgzφcgz,
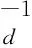



(9)
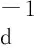
本文采用仿射线性参数变换(Egbert and Kelbert,2012)对真实模型参数进行如下转换:
(10)
(11)
在参数变换策略下,目标函数(9)修改为如下形式:
(12)
2.2 交叉梯度项计算
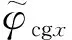
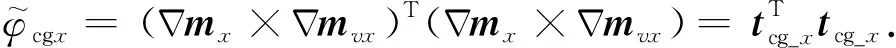
将(13)式按照三个方向进一步展开有:
(14)
参考闫政文等(2020),在式(14)中,tx_x、ty_x、tz_x三个向量的任意元素可以表述为:
(15)
其中,mx与mvx分别为X方向的某个电阻率参数和约束模型参数.对于某个具体的tx_x(i,j,z)计算,这里采用图1来说明.图1展示了一个从三维离散体抽取的二维离散面,该面是Y轴与Z轴组成的平面,以中心差分为准则,tx_x(i,j,z)可以描述为:
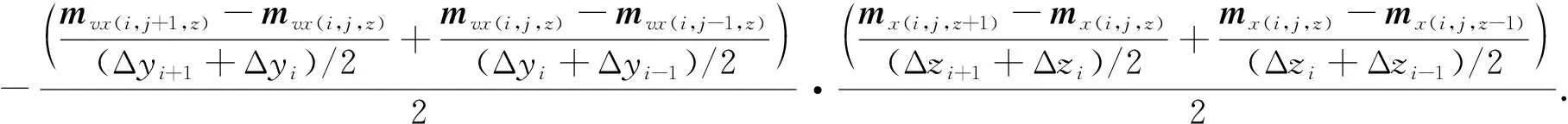
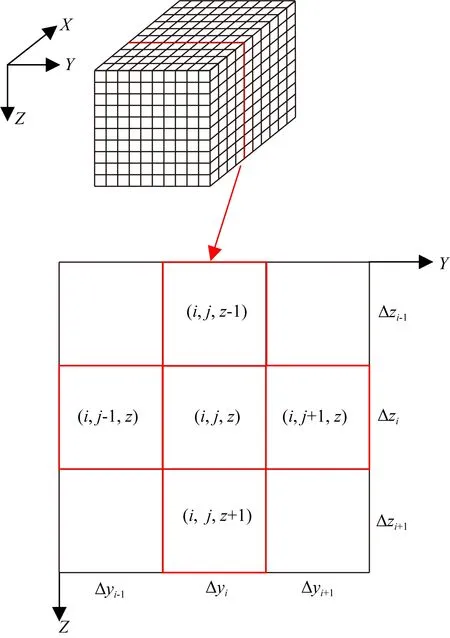
图1 从三维离散体抽取的二维离散面Fig.1 An extracted 2D discrete surface from the 3D discrete body
将式(16)整理并以矩阵形式表述如下:
(17)
其中,各元素具体形式如下:
a33=-a11-a22-a44-a55.
(18)
在图1中的内部单元循环,可以完成tx_x向量所有元素的计算.由于mvx是输入的约束模型参数,在反演中固定,实际上最终的tx_x向量是由式(17)的矩阵累加形成,最终拓展到整个模型单元可以表述为:
tx_x=Wx_cg_xmx.
(19)
同样的,ty_x、tz_x可以按照上述方式在另外两个方向离散,最终以矩阵形式表述为:
ty_x=Wy_cg_xmx,
tz_x=Wz_cg_xmx.
(20)
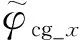
(21)
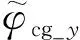

(22)
(23)
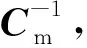
2.3 各向异性梯度计算
对于LBFGS来说,梯度计算是最重要的步骤之一,根据目标函数(12),以及式(21)(22)(23),对转换参数求导得到以下梯度表达式:
(24)
式中,数据项的目标函数具体形式如下:
(25)
其中,Re代表取实部,Jx、Jy、Jz是关于真实电阻率参数的灵敏度矩阵.对于LBFGS来说,该部分的求解技巧与NLCG (Non-Linear Conjugate Gradient,非线性共轭梯度)一致,即可通过一系列“拟正演”(Newman and Alumbaugh,2000)避免直接求解灵敏度矩阵,提高计算效率和节省大量内存.
关于式(24)后面的模型项和交叉梯度项的梯度,具体如下:
(26)
从式(25)和式(26)可以看到,要完成基于交叉梯度结构约束的MT主轴各向异性反演,梯度计算比较复杂.
2.4 LBFGS反演框架
本文的LBFGS反演流程,具体如下:
(1)选择一个反演初始模型mi,设定三个方向的正则化因子和交叉梯度权重因子;
(3)寻找一个相对合适的更新步长,以最小化φ(mi+αiui);
(4)计算更新模型mi+1=mi+αiui,判断反演是否满足停止条件,反之则开始第(5)步;
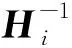
(27)
其中,si-1为模型差向量,yi-1为梯度差向量.
3 合成算例分析
3.1 各向同性模型无约束与约束反演对比
本节首先使用2.2节的交叉梯度约束项进行各向同性反演试验,以验证本文的约束方案首先能应用于各向同性介质的结构约束反演.2.2节给出的是主轴各向异性约束反演,但该方案同样可应用于各向同性反演,仅仅只需要将其他两个方向的交叉梯度约束项去掉即可.
图2为测点分布及模型俯视图,测点在X和Y方向间距160 m,共2500个测点.模型为一个低阻体(10 Ωm)与高阻体(1000 Ωm)的组合模型,并在空间上接触面较多.模型的空间分布进一步在图3第一列显示,背景电阻率为100 Ωm.为了进行约束反演研究,这里进一步建立了如图4所示的速度模型,背景值为4000 m·s-1,低速异常体为2000 m·s-1,高速异常体为6000 m·s-1.该速度异常体与电阻率的结构分布一致.
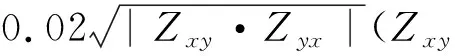
为了比较加入速度结构约束与没有速度结构约束的反演结果,使用图4建立的速度模型作为约束模型输入交叉梯度项,交叉梯度权重因子设为1.0×107,正则化因子为0.1,反演初始模型为50 Ωm均匀半空间模型.经过28次迭代后,反演拟合差从7.70下降到0.996,最终的反演结果如图3第三列所示.从图3的结果可以看到,使用交叉梯度进行结构约束后,高阻体的结构相比于无结构约束反演更加清晰,这说明本文基于交叉梯度的结构约束方案,对各向同性反演是有效的.

图2 测点分布及模型俯视图Fig.2 The measuring sites distribution and top view
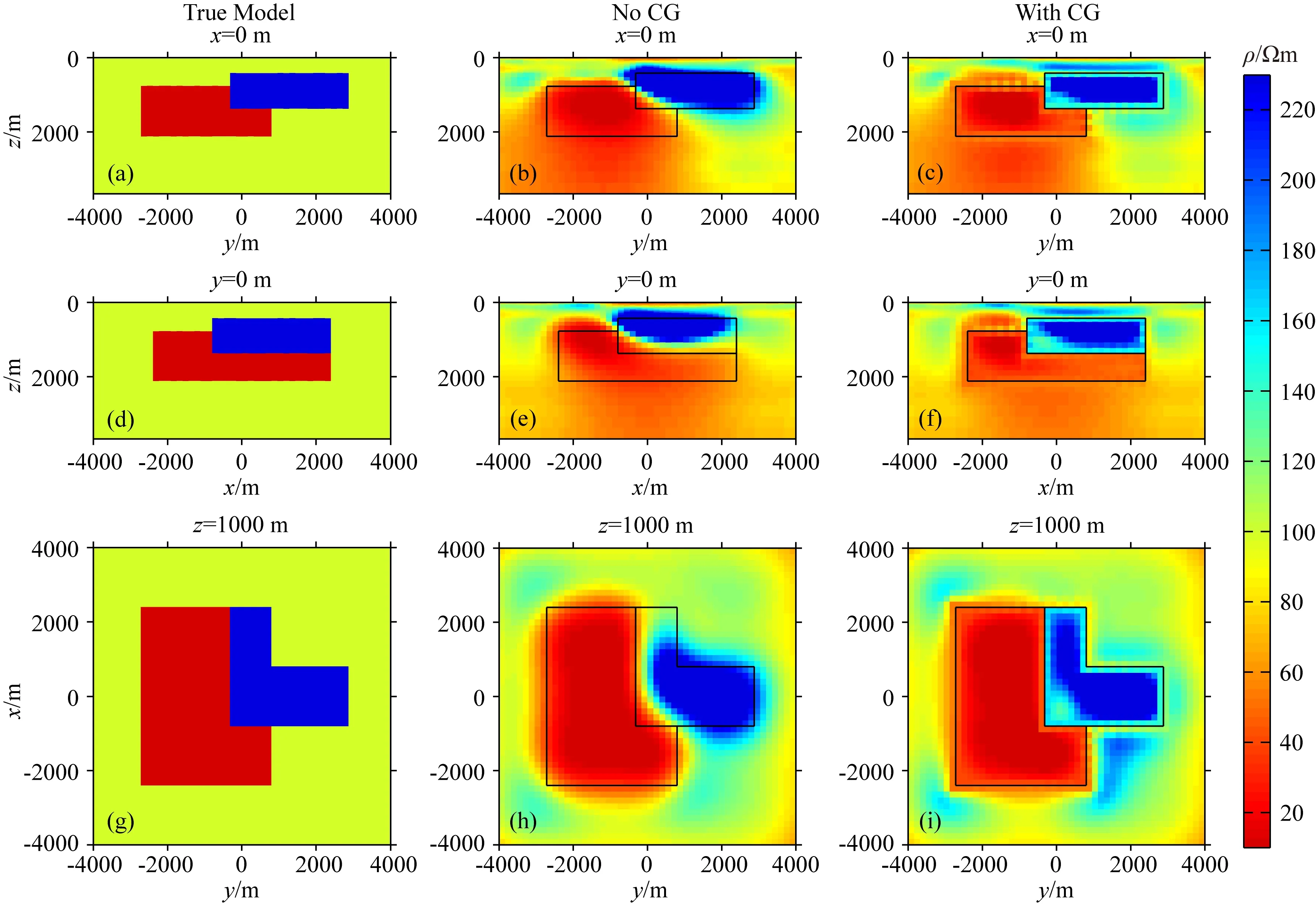
图3 第一列为真实模型,第二列为无交叉梯度约束反演结果,第三列为交叉梯度约束反演结果Fig.3 The first column is the true model.The second column is the inversion results without cross-gradient constraint. The third column is the inversion results with cross-gradient constraint
最后,我们给出了无约束反演和约束反演的步长曲线及拟合差收敛曲线(图5),可以看到本文采用的LBFGS法进行无约束与约束反演均非常稳定.此外还需要说明的是,关于本文的交叉梯度因子的选择,我们经过大量的实验后,有一个经验策略,即约束反演二次迭代的总目标函数值,相较于无约束反演二次迭代的总目标函数值提高70%~80%,约束效果及反演效率相对较好.
3.2 各向同性与主轴各向异性反演对比
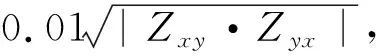
3.2.1 各向同性与各向异性无约束反演对比
为了说明在主轴各向异性明显时,各向同性反演的不足,这里首先使用无约束的各向同性与各向异性大地电磁三维反演程序对图6模型进行反演,最终的反演结果如图7所示.图7第一列是各向同性反演,第二、三、四列为各向异性反演.从图7的结果可以明显看出,当地层介质存在明显主轴各向异性时,图7第一列显示出了极强的假构造分布,对于实际情况而言这种结果会严重误导构造解释.
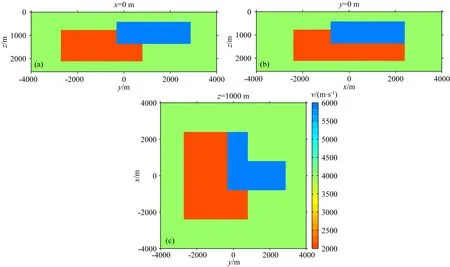
图4 用于交叉梯度约束的速度模型Fig.4 The velocity model for cross-gradient constraint
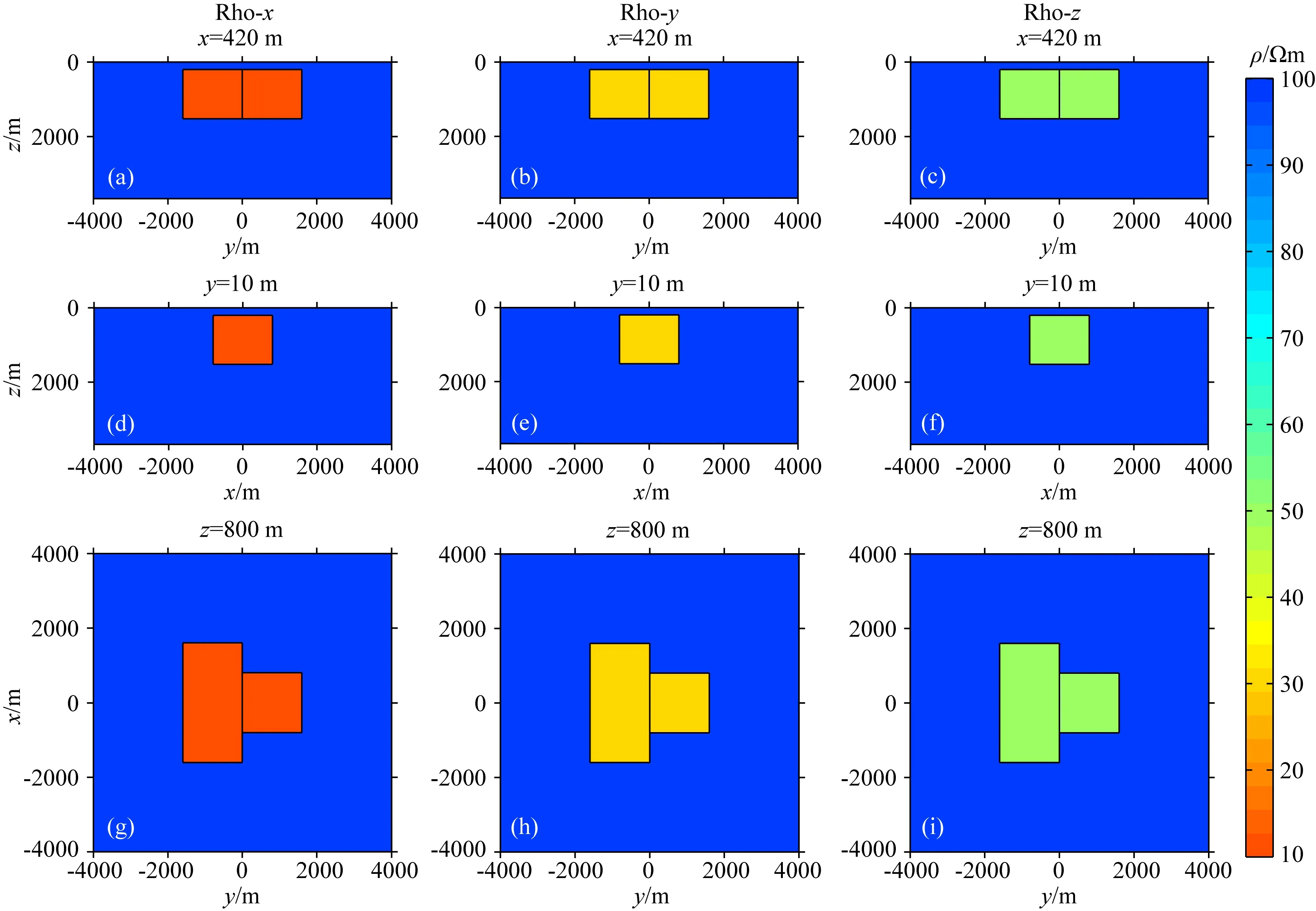
图6 第一列为X方向电阻率真实模型,第二列为Y方向电阻率真实模型,第三列为Z方向电阻率真实模型Fig.6 The first column is the true model of X direction resistivity.The second column is the true model of Y direction resistivity. The third column is the true model of Z direction resistivity
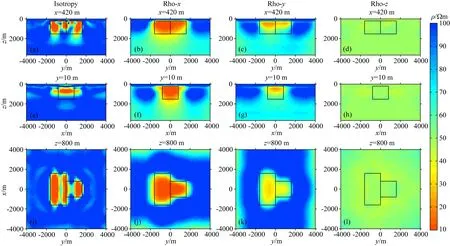
图7 第一列为各向同性反演结果,第二列为X方向电阻率反演结果,第三列为Y方向电阻率反演结果,第四列为Z方向电阻率反演结果Fig.7 The first column is the isotropic inversion result.The second column is the inversion result of X direction resistivity. The third column is the inversion result of Y direction resistivity. The fourth column is the inversion result of Z direction resistivity
图7第二列和第三列的X与Y方向电阻率反演结果,没有出现第一列强烈的假构造问题.由于X方向电阻率真实值(10 Ωm)相较于Y方向电阻率(30 Ωm)更低,而大地电磁对低阻更灵敏,因此X方向电阻率恢复情况要好于Y方向电阻率.对于第四列的Z方向电阻率,从颜色分布上有一定的扰动,但绝大多数值还是与初始模型差不多,这说明大地电磁法来自高空的平面波场源对地层的垂直电阻率不灵敏(Cao et al., 2018).
整个反演的步长曲线及收敛曲线如图8所示,各向同性与各向异性反演的最终相对拟合差分别为0.98,0.93,二者均满足收敛条件.但从迭代次数可以发现,各向同性反演迭代次数远大于各向异性,前者迭代了77次,后者仅仅迭代了11次.因此,尽管图8的步长与收敛曲线显示各向同性与各向异性反演都是稳定收敛的,但结合图7的反演结果来看,图8的曲线再一次说明若地层存在显著主轴各向异性效应时,简单的各向同性反演存在较大的不足.
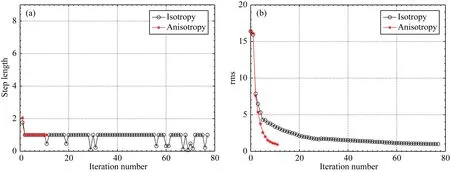
图8 (a)为步长曲线,(b)为rms曲线Fig.8 (a) is the step length curves. (b) is the rms curves
3.2.2 各向同性与各向异性约束反演对比
在本节,我们将继续使用图6模型的阻抗数据进行反演,讨论各向同性与各向异性反演在交叉梯度约束下的不同反演结果.首先建立图9所示的速度模型,背景速度值为6000 m·s-1,低速异常体速度为2000 m·s-1,该速度异常体与电阻率异常的结构分布一致.在各向同性约束与主轴各向异性约束反演中,所有的交叉梯度权重因子均为1.1×106,此外我们对各向同性以及各向异性的X、Y、Z方向的电阻率均使用图9的速度结构进行约束.
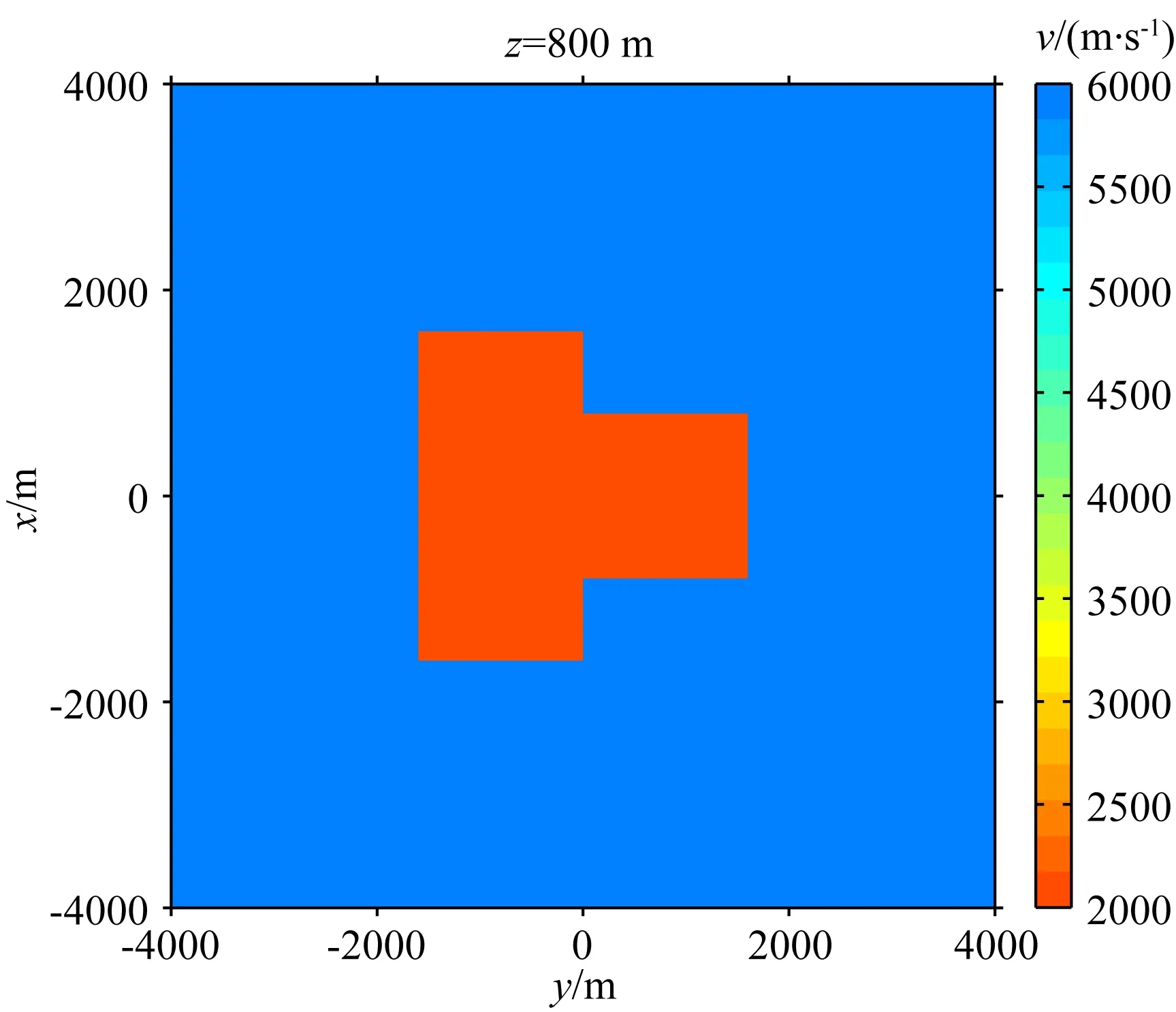
图9 用于交叉梯度约束的速度模型Fig.9 The velocity model for cross-gradient constraint
各向同性与各向异性约束反演的最终结果如图10所示,第一列为各向同性的约束反演,从这个结果可以看出,交叉梯度项对最外层边界的约束相较于图7第一列有明显的改善,但没有改变低阻体内部假构造的分布,这说明交叉梯度也无法改变各向异性介质对各向同性反演造成的干扰.
图10第二和第三列分别为X及Y方向电阻率的约束反演结果,相较于第一列而言仍然比较符合真实模型的分布.与图7第二、三列相比,边界有一定的改善,但效果不明显,主要原因是模型较为简单,我们将在下一节建立相对复杂的模型探讨交叉梯度对主轴各向异性反演的影响.
图11展示了约束下的各向同性与各向异性反演步长曲线与收敛曲线,从该结果可以看到,二者都体现了非常好的稳定性,但各向同性反演迭代次数更多,且很难达到收敛条件.图10与图11的反演结果说明当介质存在明显主轴各向异性时,对各向同性反演结果产生极大的干扰.
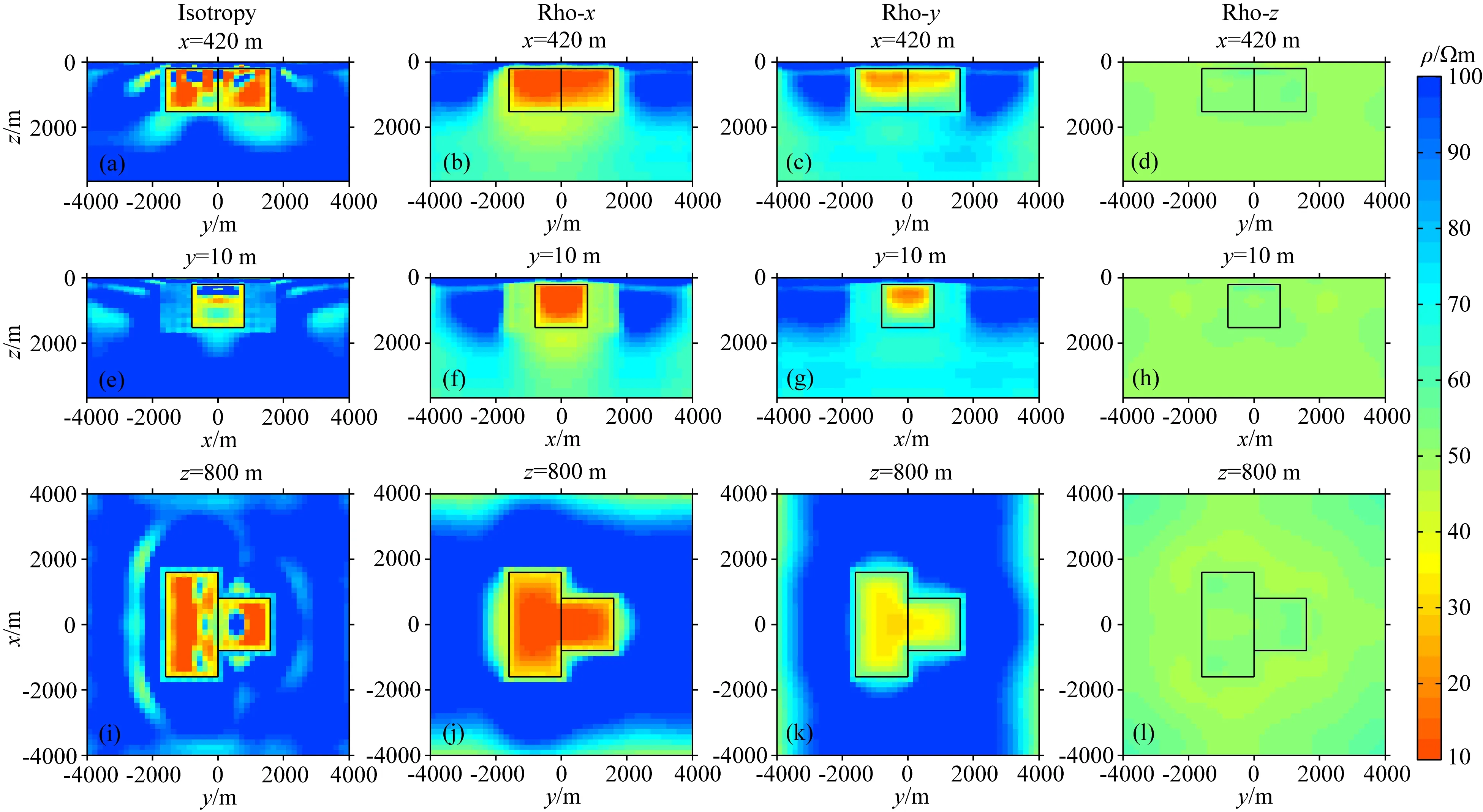
图10 第一列为各向同性反演结果,第二列为X方向电阻率反演结果,第三列为Y方向电阻率反演结果,第四列为Z方向电阻率反演结果Fig.10 The first column is the isotropic inversion result.The second column is the inversion result of X direction resistivity. The third column is the inversion result of Y direction resistivity. The fourth column is the inversion result of Z direction resistivity
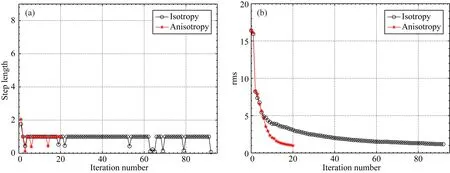
图11 (a)为步长曲线,(b)为rms曲线Fig.11 (a) is the step length curves. (b) is the rms curves
3.3 复杂各向异性模型反演
在3.2节,我们证明了在主轴各向异性效应显著时,强制使用各向同性的无约束和约束反演都会带来严重的假构造分布.由于模型较为简单,各向异性约束反演并没有特别好的体现出交叉梯度的优势和特点,本节我们将建立一个形态较为复杂的模型,探讨交叉梯度项对大地电磁主轴各向异性反演的约束效果.
之前的实验已经证明大地电磁对X及Y方向电阻率最为灵敏,而在实际地质情况中,褶皱是最有可能出现X与Y方向电阻率不同的.由于沉积作用形成的层理,在褶皱内部垂直层理和平行层理的电阻率是不同的,若出现如图12a所示的褶皱,则如图12b所示极有可能造成X与Y方向的宏观电阻率出现明显差异.
这里建立一个在地表有剥蚀的褶皱构造,共两部分组成.左边褶皱出露地表,右边褶皱顶面埋深150 m.设左右褶皱的X方向电阻率均为15 Ωm,Y方向电阻率40 Ωm,Z方向电阻率50 Ωm,背景电阻率200 Ωm,最终的模型示意图见图13第一列至第三列.本节计算频率8个,分别为100,80,50,20,10,5,0.5,0.1 Hz.正演数据添加的噪声水平,测点分布等信息与3.2节一致.在进行各向异性反演前,我们仍然先给出一个各向同性反演结果(图13第四列),初始模型为150 Ωm均匀半空间.从这个结果可以看到,左右褶皱的形态均没有正确恢复,出现了非常严重的假构造,因此实际情况的三维反演可能还需要更多的考虑.
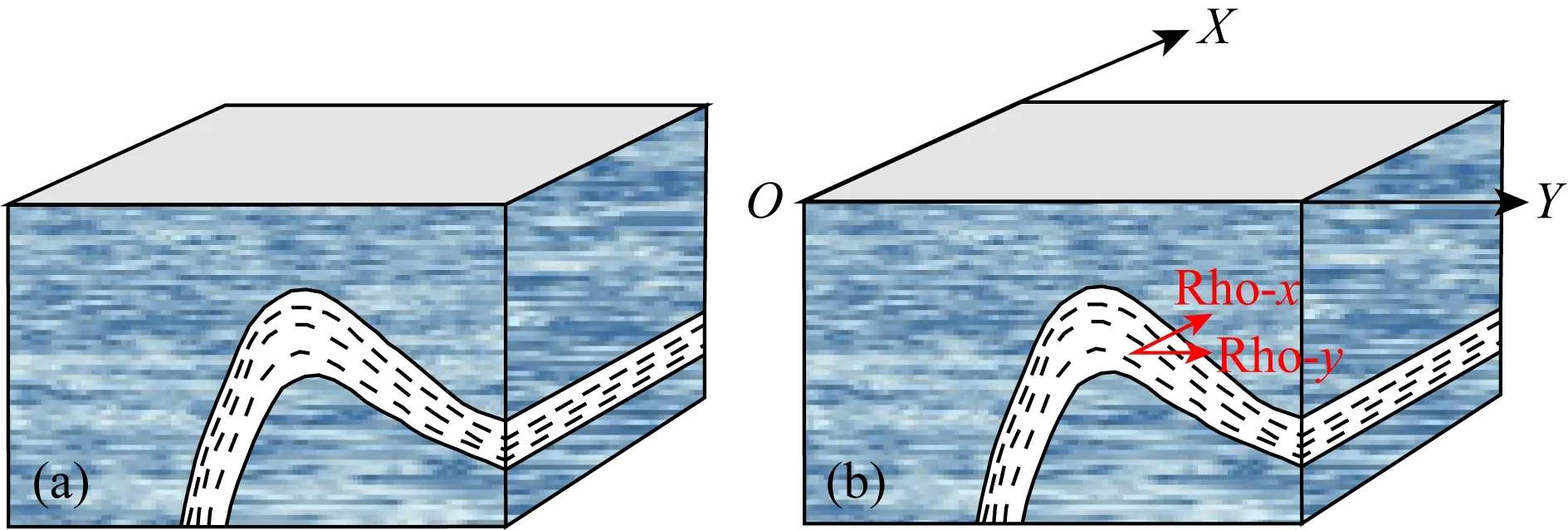
图12 褶皱示意图Fig.12 The schematic diagram of folds
现在开始进行无约束与约束的主轴各向异性三维反演,读入的约束模型如图14所示,背景速度值为6000 m·s-1,低速异常体速度为3000 m·s-1,该速度异常体与电阻率异常的结构分布一致.所有的交叉梯度权重因子均为1.5×106,三个方向电阻率均使用图14的速度模型约束.反演初始模型为150 Ωm,最终的三个方向电阻率反演结果如图15、17、19所示.针对本节的各向异性约束反演,我们并没有尝试突出某个方向的参数,因此每个方向的正则化因子都是一样的,交叉梯度权重因子也是如此.此外,交叉梯度权重因子的选择策略与3.1节中的方案一致.
首先来看图15所示的X方向电阻率反演结果,图15b和c在中深部的边界形态有明显差异,图15c的形态更接近真实电阻率的分布.为了更直观的体现反演差异,这里用图15b和c的结果分别与速度模型进行每个单元的交叉梯度项φcgx的计算,最终结果如图16所示.从图16a可以看到,无约束反演的边界与速度模型的边界有明显的交叉梯度值,这说明二者在边界形态上的变化是不一致的.在图16b中,基于结构约束后的X方向电阻率与速度模型的交叉梯度值明显降低,这个结果再一次验证了本文的交叉梯度约束是有效的.
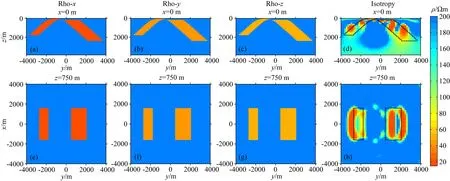
图13 第一列为X方向真实电阻率,第二列为Y方向真实电阻率,第三列为Z方向真实电阻率,第四列为各向同性反演结果Fig.13 The first column is the true model of X direction resistivity.The second column is the true model of Y direction resistivity. The third column is the true model of Z direction resistivity. The fourth column is the isotropic inversion result
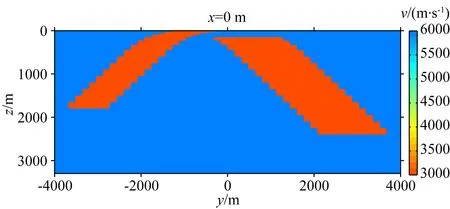
图14 用于交叉梯度约束的速度模型Fig.14 The velocity model for cross-gradient constraint
图17展示了Y方向电阻率反演结果,从图17b和c可以看到,无约束和约束后的结果依然有较为显著的差异.此外,这里给出了图17b和c的结果分别与速度模型进行每个单元的交叉梯度项φcgy的计算,最终结果如图18所示.图18a及b的φcgy分布可以看到,约束反演能较好的使Y方向电阻率结构朝着约束模型靠近.
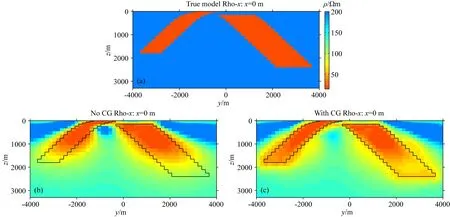
图15 (a)为X方向真实电阻率, (b)为无约束的X方向电阻率反演结果, (c)为使用结构约束的X方向电阻率反演结果Fig.15 (a) is the true model of X direction resistivity. (b) is the inversion result of X direction resistivity without constraint. (c) is the inversion result of X direction resistivity with structural constraint
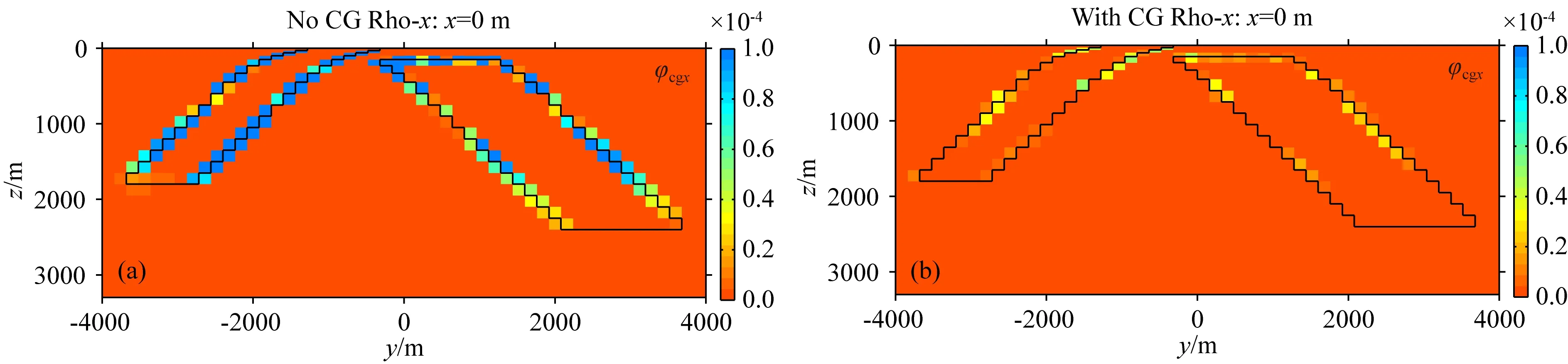
图16 (a)为图15b与速度模型的交叉梯度项φcgx分布, (b)为图15c与速度模型的交叉梯度项φcgx分布Fig.16 (a) is the cross-gradient φcgx distribution of Fig.15b and velocity model. (b) is the cross-gradient φcgx distribution of Fig.15c and velocity model
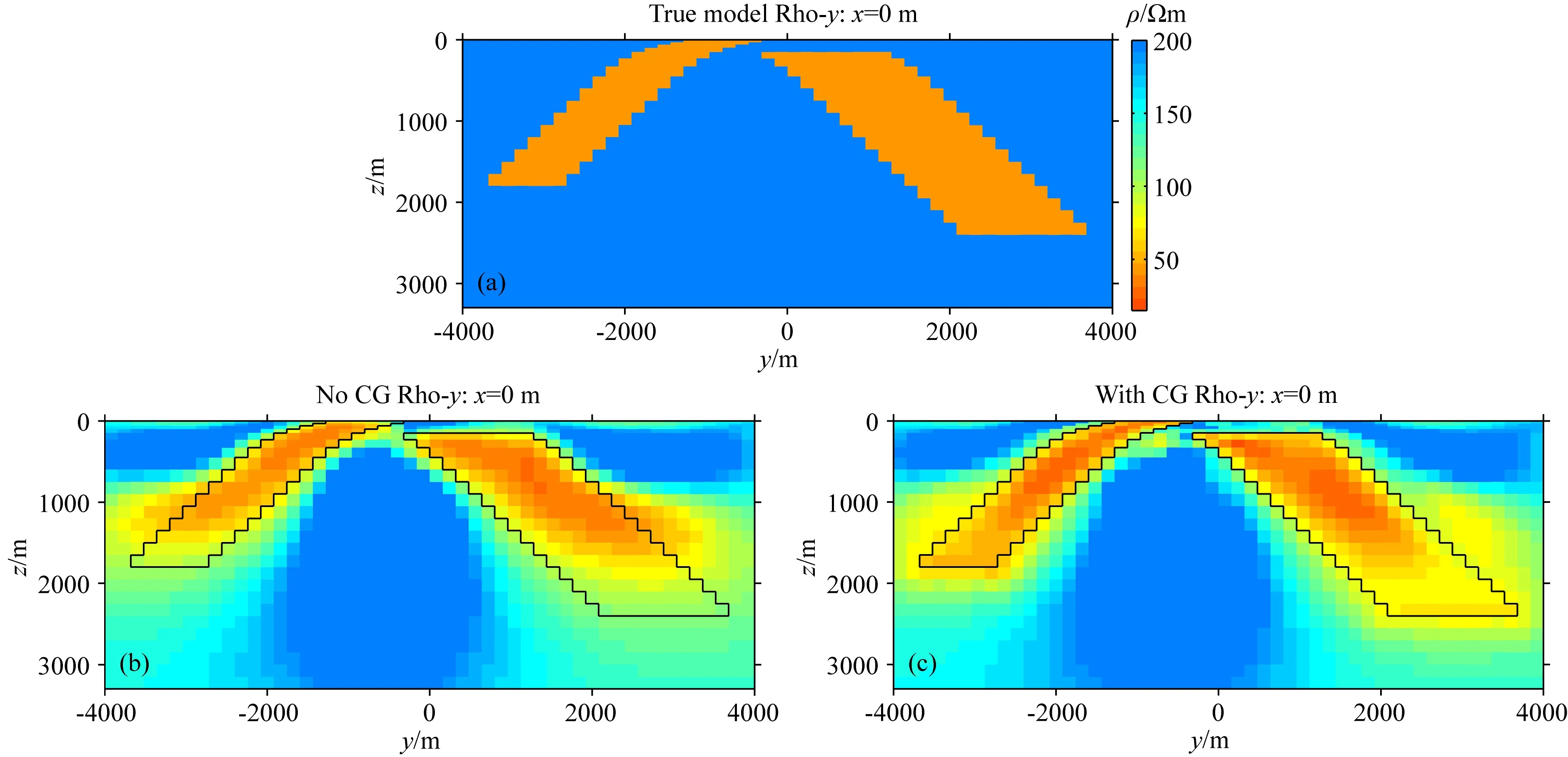
图17 (a)为Y方向真实电阻率, (b)为无约束的Y方向电阻率反演结果, (c)为使用结构约束的Y方向电阻率反演结果Fig.17 (a) is the true model of Y direction resistivity. (b) is the inversion result of Y direction resistivity without constraint. (c) is the inversion result of Y direction resistivity with structural constraint
图19为Z方向电阻率反演结果,图19b和c的结果相较于图7与图10中的Z方向电阻率反演结果而言,有更好的扰动结果.但实际上图19中的无约束和约束结果都只能反映Z方向电阻率浅部的大致形态,背景值及整体分布都没有正确的还原,该结果再一次说明MT对垂直方向电阻率的灵敏度很弱.我们在图20a与b中分别给出了无约束及约束后的Z方向电阻率与速度模型每个单元的φcgz分布,这里依然可以看到约束后的模型交叉梯度值更小.
在图21中分别显示了各向同性、无约束各向异性、约束各向异性反演的步长曲线及收敛曲线,从步长曲线可以看到,各向同性反演在最后阶段的反演步长都不为1,这反映出LBFGS在收敛中遇到了拟牛顿方向不稳定的情况,说明当介质具有较强各向异性效应时,常规的各向同性反演不适用.此外,从rms收敛曲线也可以进一步观察到,各向同性反演很难达到收敛停止条件.本节的模型反演实验再一次展示了各向异性对反演带来的影响是非常显著的,在实际应用中应该特别注意,尤其是大构造的解译是否有必要考虑各向异性效应,以尽可能减少冗余构造的出现.

图18 (a)为图17b与速度模型的交叉梯度项φcgy分布, (b)为图17c与速度模型的交叉梯度项φcgy分布Fig.18 (a) is the cross-gradient φcgy distribution of Fig.17b and velocity model. (b) is the cross-gradient φcgy distribution of Fig.17c and velocity model
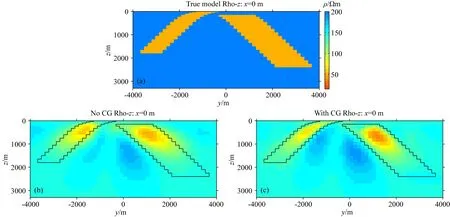
图19 (a)为Z方向真实电阻率, (b)为无约束的Z方向电阻率反演结果, (c)为使用结构约束的Z方向电阻率反演结果Fig.19 (a) is the true model of Z direction resistivity. (b) is the inversion result of Z direction resistivity without constraint. (c) is the inversion result of Z direction resistivity with structural constraint
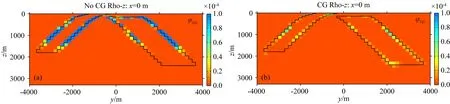
图20 (a)为图19b与速度模型的交叉梯度项φcgz分布, (b)为图19c与速度模型的交叉梯度项φcgz分布Fig.20 (a) is the cross-gradient φcgz distribution of Fig.19b and velocity model. (b) is the cross-gradient φcgz distribution of Fig.19c and velocity model
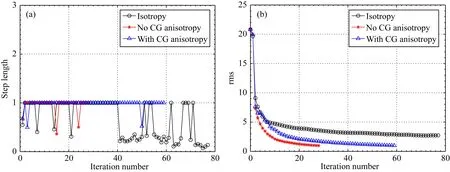
图21 (a)为步长曲线, (b)为rms曲线Fig.21 (a) is the step length curves. (b) is the rms curves
3.4 并行效率分析
由于主轴各向异性正反演仍然具备频点、XY及YX模式相对独立的计算任务,因此很容易使用MPI技术实现粗粒度并行.这里使用3.2节的各向异性正演计算进行并行效率分析,运行的系统为Centos Linux系统,内存32 G,工作站最大可开辟24进程.我们分别使用1,2,4进程数,来展示总体耗时和加速比.表1统计结果表明,三维并行程序得到了接近线性的加速比,体现了较好的并行度.
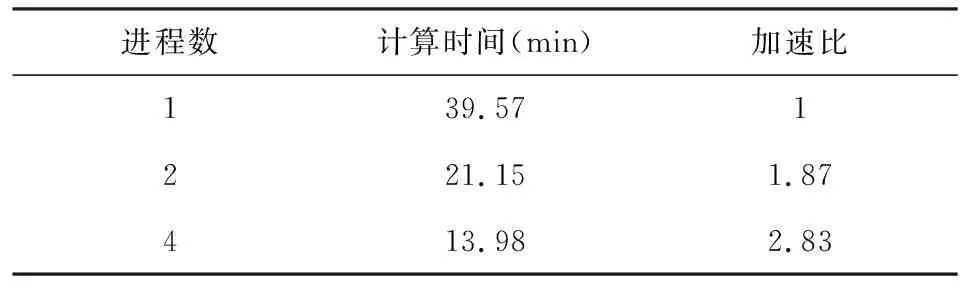
表1 使用不同进程数的耗时及加速比Table 1 The consuming time of adopting different processes and speed-up ratio
4 结论
在复杂工区开展多方法地球物理勘探,已经是目前常用的流程.本文的目的就是希望能为大地电磁反演输入一种先验的结构信息,以达到进一步提高大地电磁反演分辨率的目的.基于此,本文开展了基于交叉梯度结构约束的大地电磁主轴各向异性三维反演研究.为了实现结构约束,在各向异性反演目标函数中加入了交叉梯度约束项,可输入任意结构实现本文提出的主轴各向异性结构约束.反演采用了LBFGS法,并进一步利用MPI技术实现了并行加速,得到了较好的加速比.本文的模型试算可以得到如下结论:
(1)基于交叉梯度的结构约束方案,可以对各向同性与主轴各向异性模型起到较好的结构约束效果,在一定程度上改善了大地电磁单方法反演的分辨率;
(2)若地下介质存在显著的主轴各向异性时,强制使用无约束或约束的各向同性反演,均会造成地下结构出现严重的假异常.这种情况的出现,可能会对实际构造的解释产生极大的干扰,不利于最终的地质建模及解释.

