基于运动控制的加减速阶段减振方法研究

夏飞扬， 樊可清

(五邑大学 信息工程学院，广东 江门 529020)

运动控制系统的减振一直都是运动控制系统研究的关键技术，因为系统的振动会严重影响运动控制系统的加工效率和精度。如CNC系统的振动会影响系统的加工精度和机器的寿命，机器人运动的平稳性与其系统振动控制密切相关，机械手的振动会严重影响其定位精度和工作效率，吊车的摆动不仅会影响工作效率甚至还会影响操作人员的生命安全等[1-3]。可见运动控制系统的振动控制问题已成为运动控制产业能否广泛和进一步应用的关键。

文献[4]～文献[7]通过应用输入整形的方法来抑制机器人柔性臂的残余振动，虽然在一定程度上可以抑制振动，但增加了系统的总运动时间。文献[8]～文献[10]提出了减少加减速阶段计算量的方法，通过减少加减速段的计算量可以增强系统的实时性，在一定程度上可以抑制系统的振动，但这种方法的抑制效果毕竟是较差的。文献[11]引入了PID控制来抑制系统振动的方法，这种方法对系统模型要求非常高，对非线性系统的振动抑制程度很有限。

目前提出的运动控制减振算法大都着重考虑系统的整个运动过程，这就使得所设计的减振控制器比较复杂同时极大地增加了系统的计算量，从而使得控制器的实时性不好，而实时性是保证闭环控制系统稳定性的首要条件，这将会导致设计的控制器不稳定，这就是为什么很多控制方法很难在实际工程中运用的原因。根据理论，系统的振动是由加减速阶段引起的，可以研究控制系统的加减速频谱和系统振动频谱的关系，从而只在加减速阶段着手来设计控制器，这样可以大量减小计算量从而增强控制器的稳定性，以此来优化控制算法在实际工程中的运用。通过大量阅读文献发现目前还没有研究者真正在实际工程中研究运动控制系统的加减速频谱和系统振动频谱的关系，所以笔者设计了一个运动控制系统，来研究实际工程中加减速频谱和系统振动频谱的关系，然后通过控制加减速阶段振动的条件来规划加速度，通过仿真实验结果可以发现规划算法可以确保运动系统在加减速阶段的摆动角度为零。

1 加速度频谱和系统振动频谱关系研究

1.1 S曲线速度规划模型

高速高质是运动控制产业追求的目标，这就要求运动控制系统快速达到指定的设定速度并平稳停止在指定的位置。但由于系统本身的特性使得运动系统在运动过程中会有一个加减速的过程，这个过程很容易激起系统的振动模态从而引起系统的振动，这就要求规划好加减速从而实现运动控制系统的柔性加减速以便减小起停时系统的振动使系统快速停止，从而加快系统的运作效率[12]。

现有的加减速算法有直线加减速控制方法[13]、指数加减速控制方法[14]和S曲线加减速控制方法[15]等。直线加减速控制方法虽然计算简单，但它的加速度不连续会引起很大的冲击；指数加减速控制方法的加速度虽然连续但其计算复杂影响系统的实时性；S曲线加减速控制方法加速度连续，计算量小于指数加减速控制方法，是目前比较常用的一种控制方法。本文首先通过采用S曲线加减速控制方法来控制设计的二阶单摆系统运动，采集在不同加减速时间下系统振动数据，再通过FFT变换分析系统加速度所含的频率成分和系统振动频率成分的关系；然后根据前面的实验结论来规划加速度，在确保系统在起停时的摆动为零的条件下得到加速度曲线中的相关参数。通过仿真可以发现本方法可以确保系统在起停时的振动加速度为零，控制了系统在起停时的振动，这就可以使运动系统快速停止在指定的位置，从而提高了运动控制系统的工作效率。

在研究加速度频谱和系统振动频谱的实验中采用的是常规7段S型加减速控制方法，实验运动的行程是单点的直线运动，并且起始速度为零，如图1所示，整个过程由加加速度、匀加速度、减加速度、匀速、加减速、匀减速及减减速7段组成[16-17]。

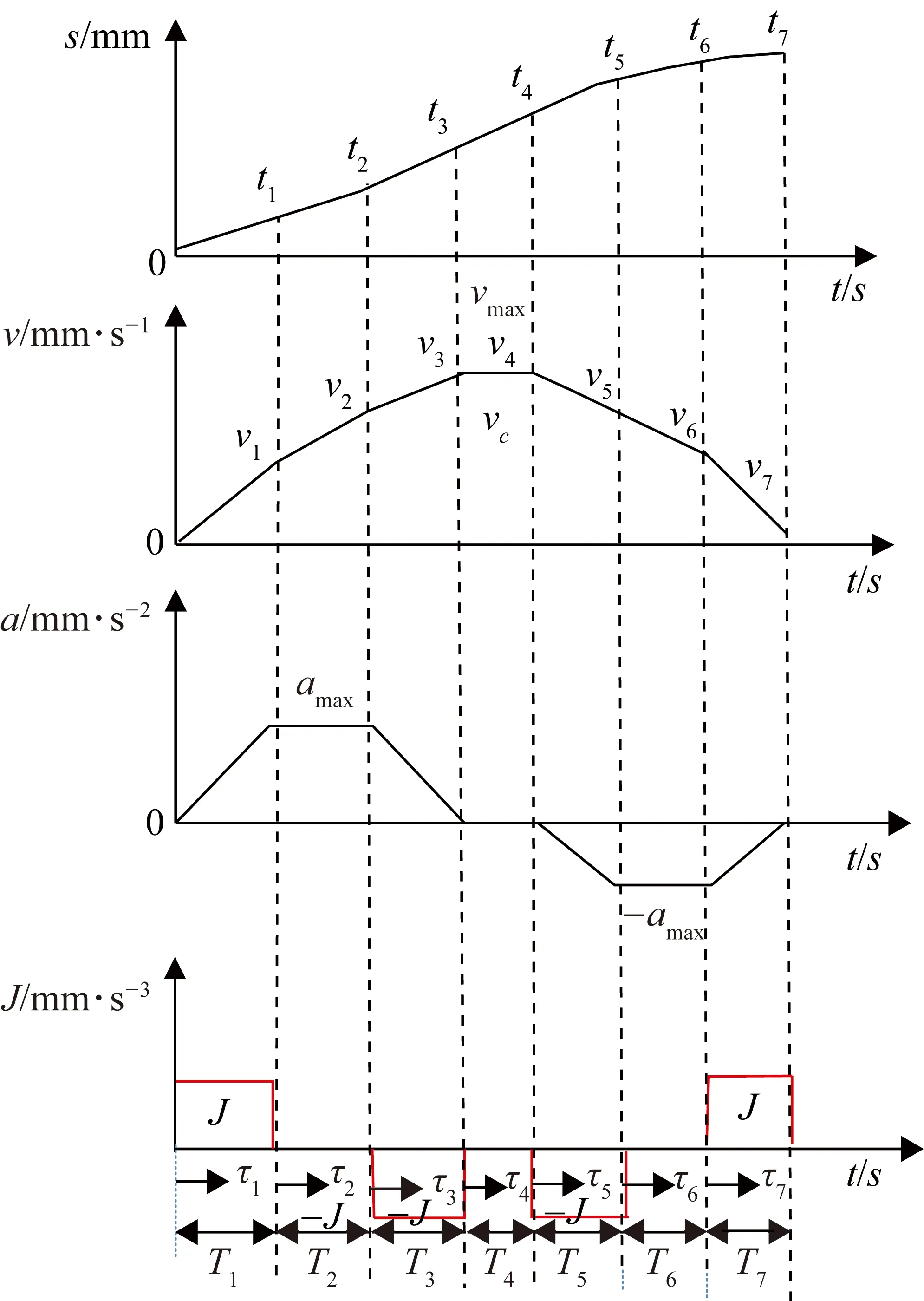
图1 S型加减速运动过程

图1中，vc为指令速度，vmax为运行的最大速度，tk(k=1,2,…,7)为各阶段的过渡点时刻；vi(i=1,2,…,7)为各阶段的过渡点时刻的速度；τk(k=1,2,…,7)为局部时间坐标，表示以各阶段的起始点作为零点的时间,τk=t-tk-1;Tk(k=1,2,…,7)为各个阶段的持续运行时间；amax为最大加速度；J为加加速度；L为整个运行长度。

其中加加速度J在运动过程中的取值为

(1)

而加速度a(t)、进给速度v(t)和位移s(t)之间的积分关系

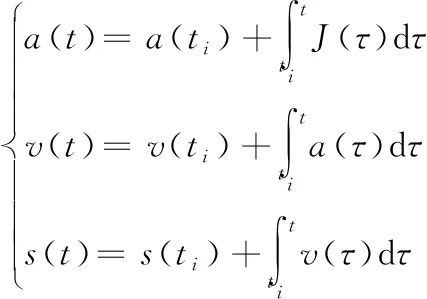
(2)

即可得到加速度a(t)、进给速度v(t)和位移s(t)在运动过程中的取值：

(3)

(4)

(5)

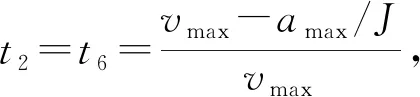
(6)

因此，只要确定vmax，amax，J，就可以确定整个运动过程。

1.2 运动系统模型

一个系统有无数阶振动模态，但通常起主要作用的往往只有前两阶，所以在本实验中用两个质量铝块和钢直尺来等效一个二阶的系统。本实验的运动控制系统如图2所示，两个铝块拴紧在钢直尺的不同位置上，在铝块上分别粘贴传感器来测量铝块的振动，钢直尺的上端固定在横梁的滑块上，横梁固定在刚性圆柱支架上，每个圆柱支架的底座都有防振脚垫，来减少其他振动的干扰，横梁的一端固定有PANATERM A5伺服电机。本实验的控制采集系统如图3所示，控制机箱是NI的cRio9033，该机箱配有可重置的FPGA和基于RT的系统，从而确保了系统的实时性。振动信号的采集是采用NI 9239采集卡，最大采样率50 kS/s，A/D分辨率达24位，确保足够的采样精度。运动控制卡采用NI的9512，该运动控制卡可以设置梯形、S型、三角函数型等多种控制模式，而且可以读取编码器反馈的信号，方便了系统的准确调试。

图2 运动系统

图3 控制采集系统

1.3 实验结果

在实验开始时先用力敲击钢直尺，通过铝块上的加速度计可以采集到敲击后的振动信号，再通过傅里叶变换可以得到系统的固有频率。通过多次实验得到本系统振动频域如图4所示，可知本系统的第一阶固有频率为0.84 Hz，第二阶固有频率为4.75 Hz。

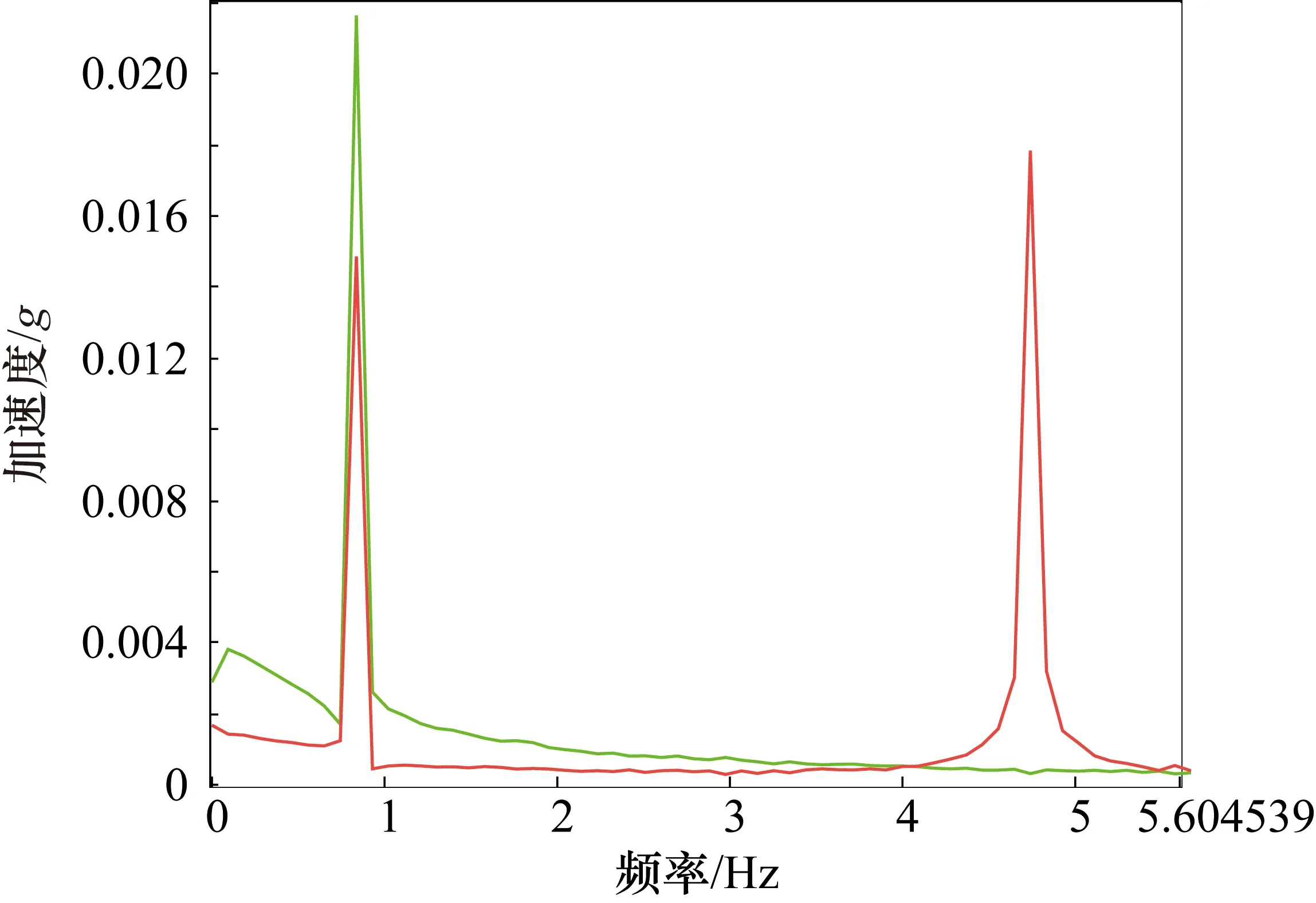
图4 系统第一、二阶固有频率图

实验时设置系统的总行程L=1000 mm,系统总的运行时间t=12 s,本实验是为了研究加速度的频谱和系统振动的频谱之间的关系，所以通过控制加速度的时间来控制加速度频带的宽度，对比在加速度包含的频率成分及幅值不同时，系统振动频率的变化。本实验中设置两个加速度时间，分别为0.25 s和5 s，为防止偶然因数的影响，每个加速度时间下的实验重复5次，再在5次中取偶然因数影响最小的一次作为本实验的测试结果，得到两种不同加速度时间下的加速度时频图和对应的系统振动时频图，分别如图5～图10所示。

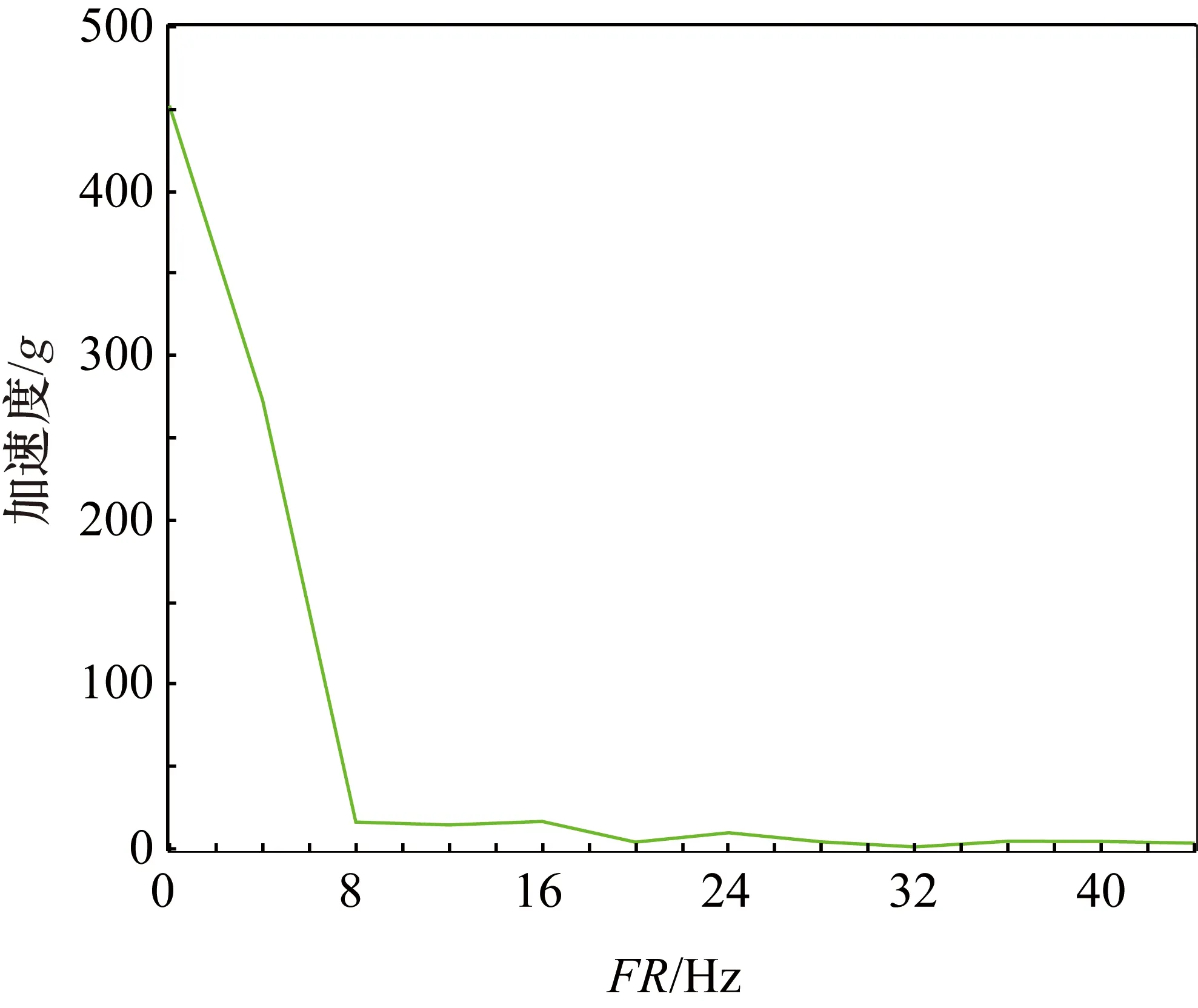
图5 加速时间0.25 s频域图

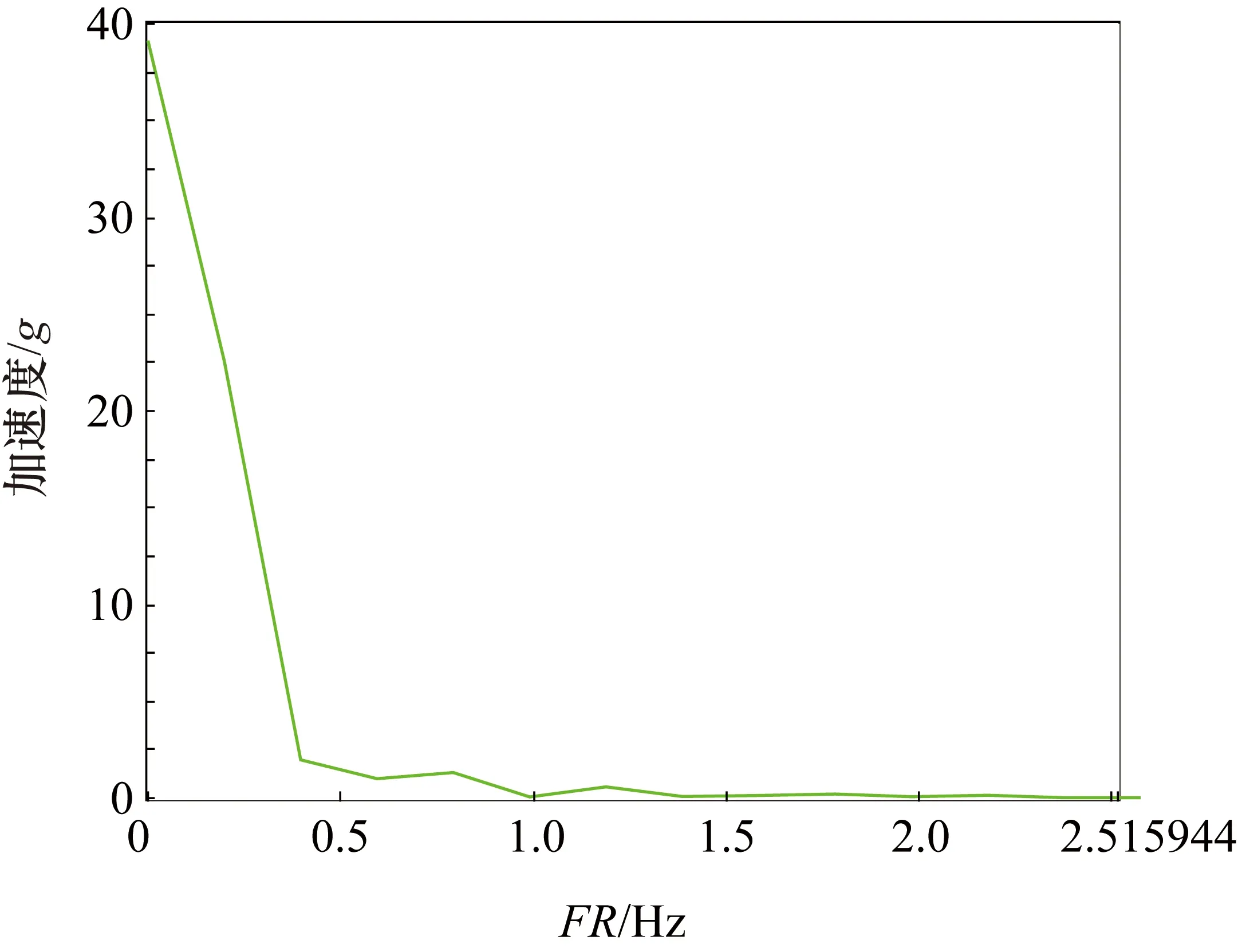
图6 加速时间5 s频域图

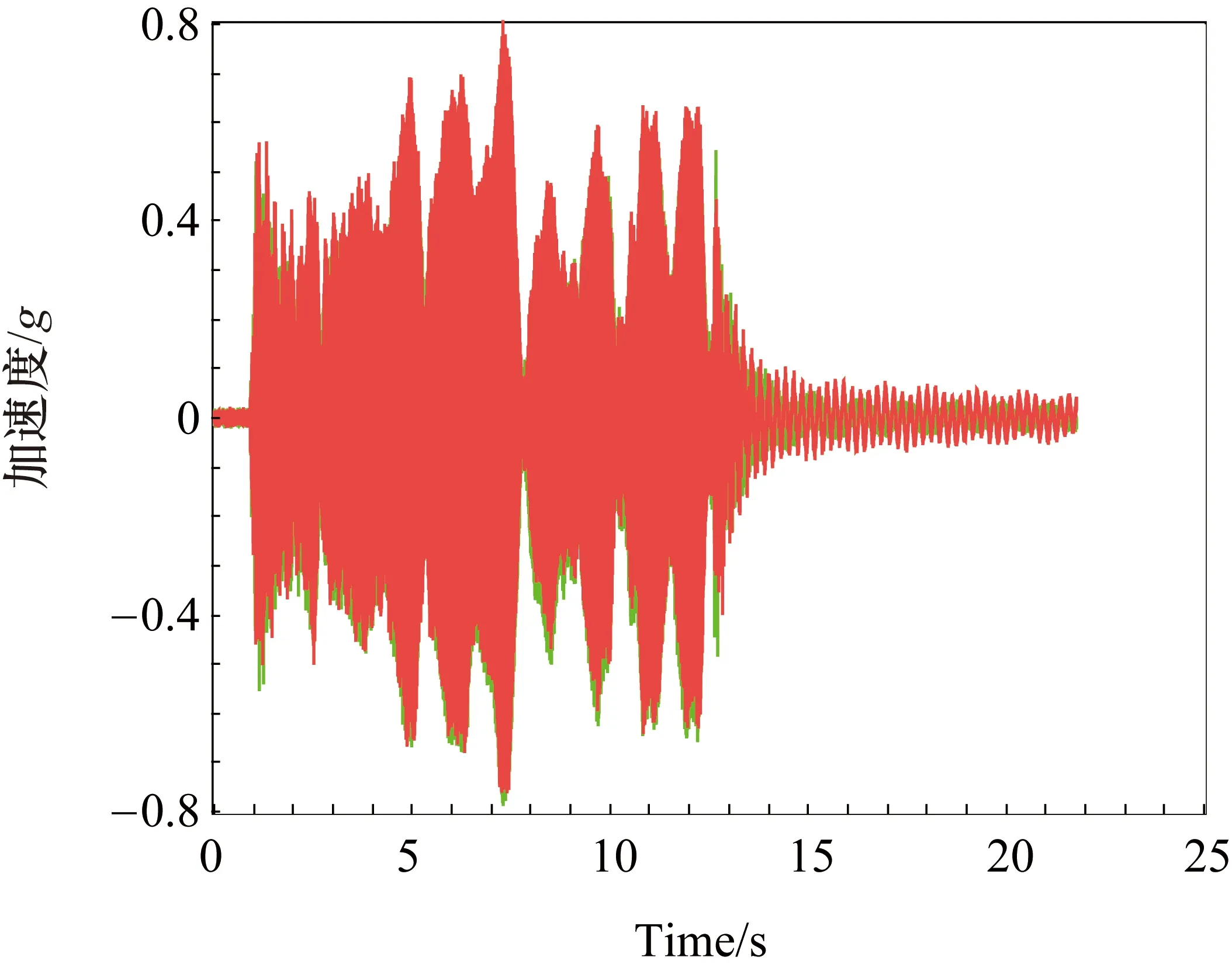
图7 加速时间0.25 s时系统振动时域图

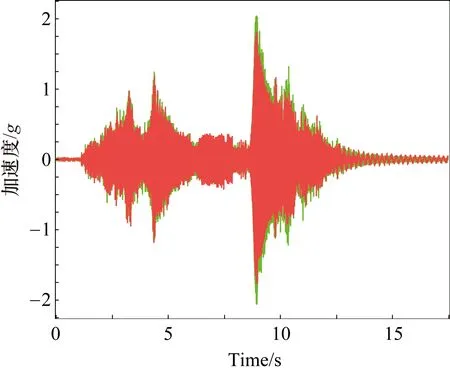
图8 加速时间5 s系统振动时域图

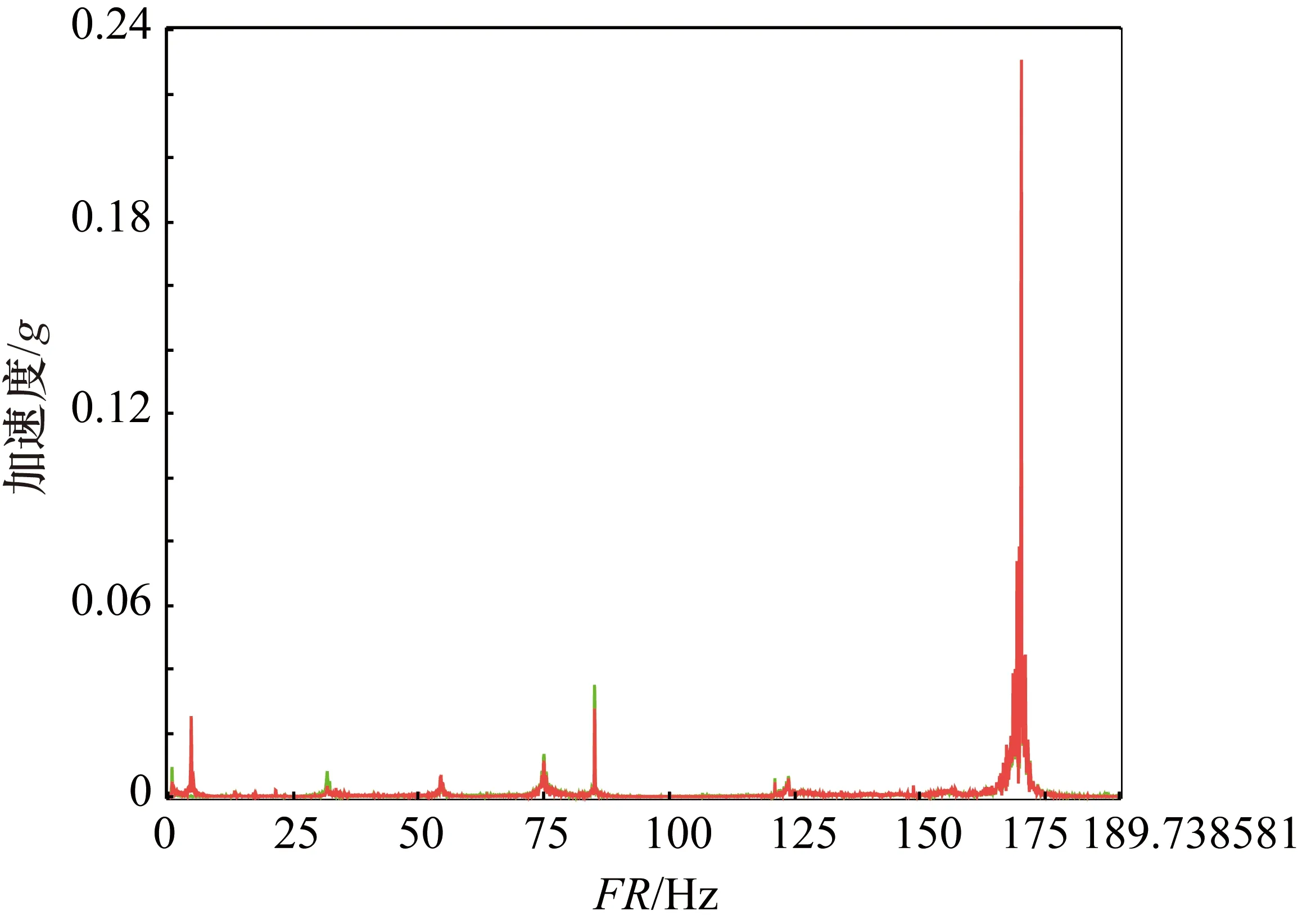
图9 加速时间0.25 s系统振动频域图

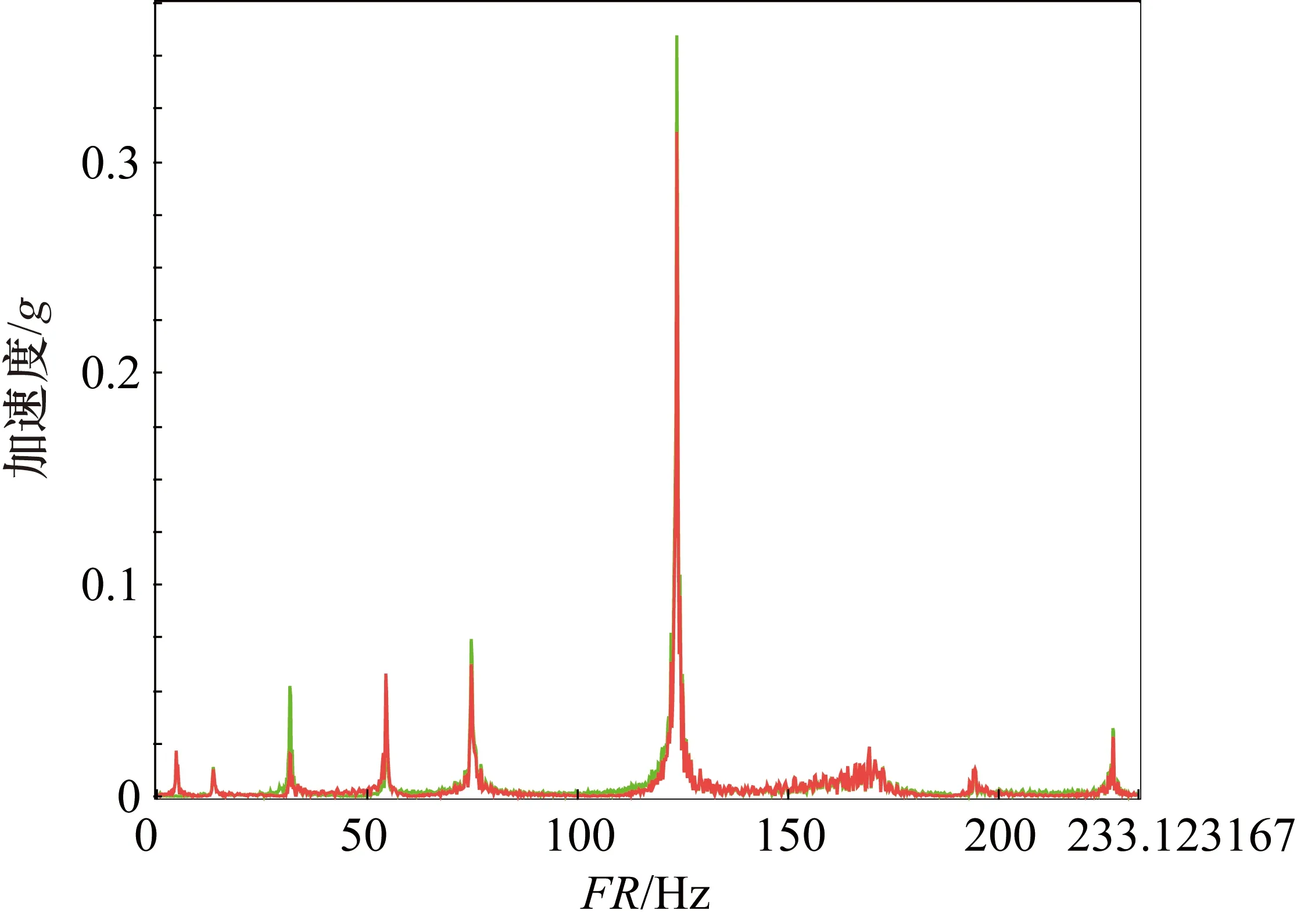
图10 加速时间5 s系统振动频域图

通过对比电机加速度频谱和系统振动频谱发现，系统振动频谱中包含有加速度频谱中没有的成分，所以系统的振动并不是完全由电机引起的，可能还有摩擦等其他激励系统的振动。

1.4 结论

① 在实验过程中发现加速阶段含有系统固有频率成分的幅值越大，系统摆动的幅度就越大，停止时所花费的时间就越长，这可能是加速度引起了系统共振的结果。

② 从系统振动的时域图可以发现，系统的振动主要是在起停阶段，因此要想减小系统的振动只需规划好系统的加减速，而且在实际工程中也是起停阶段的振动降低了工作效率。

③ 通过对比分析加速度频域图和系统振动频域，可以发现系统振动的频谱图中包含了加速度信号中没有的频率成分，这可能是实际工程中系统运动滑块的不平滑、连接部位的刚度不够等引起的冲击性或强迫性的振动。

2 规划加速度减振仿真实验

2.1 系统模型

设计本仿真实验的系统物理模型如图11所示。

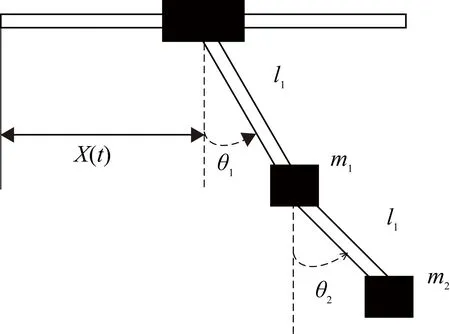
图11 二阶系统物理模型

由拉格朗日方程可得系统的数学模型如下：

(7)

要想系统到达指定的位置并且在起始时的摆动角度为零就得满足

(8)

由运动系统本身的特性，在运动过程中的速度和加速度有极限条件，即

(9)

2.2 规划满足约束条件的加速度

由前面实验发现系统的振动主要在加减速阶段并且实际工程中影响工作效率的也是在起停阶段，因此可以只通过规划加速度来控制系统的振动以简化控制器、减少计算量从而提高控制器的鲁棒性，以便更广泛地应用于实际工程中。在实验中重新规划的加速度公式如下：

(10)

式中，k，b为常数,现通过约束条件式(8)、式(9)来确定加速度(10)中参数k，b,t1～t7的值。通过分析发现t1可以通过式(11)确定

(11)

k可以通过迭代学习公式(12)得到满足相应条件下的值。

(12)

式中，T为迭代的时间间隔；kk为自学习的参数。参数b可以通过式(13)得到。

b=kt1

(13)

t2跟最大速度和运动的行程有关，即

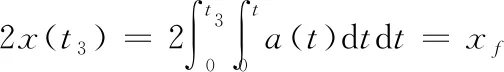
(14)

而t3=t2+t1，t4可由式(15)得到。

2x(t3)+v(t3)·(t4-t3)=xf

(15)

由运动时加速度和减速度的对称性，可以得到t5，t6，t7：

t5=t4+t1
t6=t4+t2
t7=t4+t3

(16)

2.3 Matlab仿真实验

通过大量实验发现这种通过规划加速度来控制运动控制系统起始摆动的方法鲁棒性高、计算量少，并可以保证运动控制系统在起始的摆动角度为零。本实验中选取的参数如下：g=9.8 m/s2,am=1 m/s2，vm=1.5 m/s,θm=0.1 rad,xf=10 m,l1=1 m,l2=0.5 m，m1=1 kg,m2=3 kg。得到的仿真结果如图12所示。

从仿真结果可以看出，在起停时刻的振动角度为零，所以提出的通过规划加速度来控制运动控制系统的振动算法是有效的。

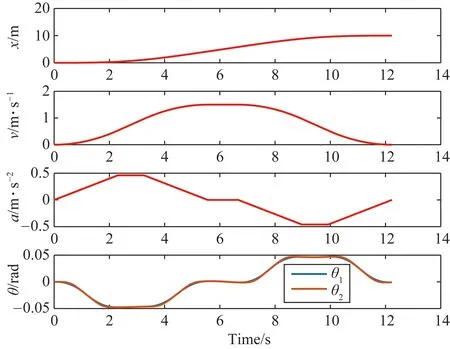
图12 仿真实验结果图

3 结束语

由于目前提出的运动控制算法比较复杂、计算量大，因而很难在实际工程中应用。考虑到在实际工程中影响系统效率的主要是加减速阶段系统的振动，所以本文从引起系统振动的加减速阶段入手，首先分析了在实际工程中加速度频谱和系统固有振动频谱的关系，发现系统振动频谱中含有加速度频谱中没有的频率成分，所以单靠去除加速度中系统的固有频率的话系统还是会被引起冲击性的振动，所以就通过约束加减速过程的振动来规划加速度曲线，通过实验发现可以保证运动控制系统在起停时的摆动角度为零。