风电叶片多点静力测试神经网络PID解耦控制

周爱国， 曾智杰， 乌建中， 张金峰

(同济大学 机械与能源工程学院，上海 201804)

风电叶片全尺寸结构静力测试是通过载荷等效模拟的方法来验证叶片在极限载荷条件下的承受能力，以确保叶片实际运行的安全可靠。叶片静力加载测试方法的正确性和测试参数的准确性对于保证叶片质量具有重要意义。叶片在进行多点加载测试时，各加载节点存在相互耦合干扰的问题，造成系统载荷波动振荡，控制精度下降，这种多点加载交联耦合现象是叶片静力加载过程中普遍存在的问题[1]。

针对上述问题，目前主流的解决方案分为两种：建立叶片静力加载模型，设计对应的解耦控制器；通过自整定控制算法实时修正控制参数，以达到解耦的效果。由于实际测试时往往无法知晓叶片刚度、弹性模量等具体参数，很难对每一个叶片建立精确的耦合模型并设计相应的解耦算法。因此，可以针对不同叶片自动调节控制参数的自整定算法得到越来越多的关注与研究，如黄雪梅、张磊安等提出一种模糊控制与预测理论相结合的动态控制算法以实现风电叶片五节点静力加载解耦控制；乌建中等[2]通过BP神经网络PID自整定算法实现了三点静力加载的解耦控制。本文在其基础上针对神经网络收敛速度慢、易陷入局部最优等问题，提出一种变步长BP神经网络PID自整定算法，对其反向传播的过程进行了优化，并且于神经网络的输入端通过归一化处理解决了3项输入间数量级相差较大的问题。

本文首先对现有的BP神经网络算法进行改进，设计了变步长BP神经网络PID自整定算法。利用Simulink构建伺服电机多点加载控制模型，对比传统PID算法，验证该BP神经网络算法的解耦能力，通过改变刚度和耦合矩阵的方式测试其自适应性能。最后在现场试验中，验证了该算法可以对6点静力加载耦合系统实现解耦。

此前的一些自整定控制算法，包括模糊控制、传统的BP神经网络等，大都只适用于5点以下的静力加载系统。本文提出的算法经过现场试验验证了其6点加载解耦控制的精度，对于将来6点及以上的叶片多点静力加载解耦控制具有指导意义。

1 风电叶片多点静力加载系统

叶片静力测试中，为使测试弯矩分布与设计弯矩分布尽可能吻合，多采用多点加载方式，并据此确定各点处的加载力，如图1所示。大型风电叶片全尺寸结构静力测试如图2所示，叶片根部通过法兰螺栓固定于加载基座上，加载系统通过加载支架上的卷扬绞车侧向加载，绞车由电液或电动伺服系统驱动，收紧或放松钢丝绳，以此对叶片进行加载或卸载。由加载缆索上的力传感器反馈，通过控制算法协调各加载节点的载荷，实现各加载节点的比例同步闭环控制[3]。

若采用通常的PID控制算法来进行各节点的加载控制，则由于叶片的大柔度非线性特性，各加载节点的挠度不仅与其自身载荷有关，还受其他各节点载荷的影响，各节点挠度和载荷将产生不同程度的交叉干扰情况，这种情况称之为“交联耦合”。实际加载力在跟踪预设目标值的过程中会产生剧烈振荡，如图3所示。

以三点加载为例，假设在叶片3个不同节点分别施加载荷F1、F2、F3，对应的挠度分别为y1、y2、y3，耦合效应会造成节点1处的挠度y1不仅取决于自身的载荷F1，同时与F2、F3相关，三点静力加载各载荷交联耦合的传递关系如图4所示。

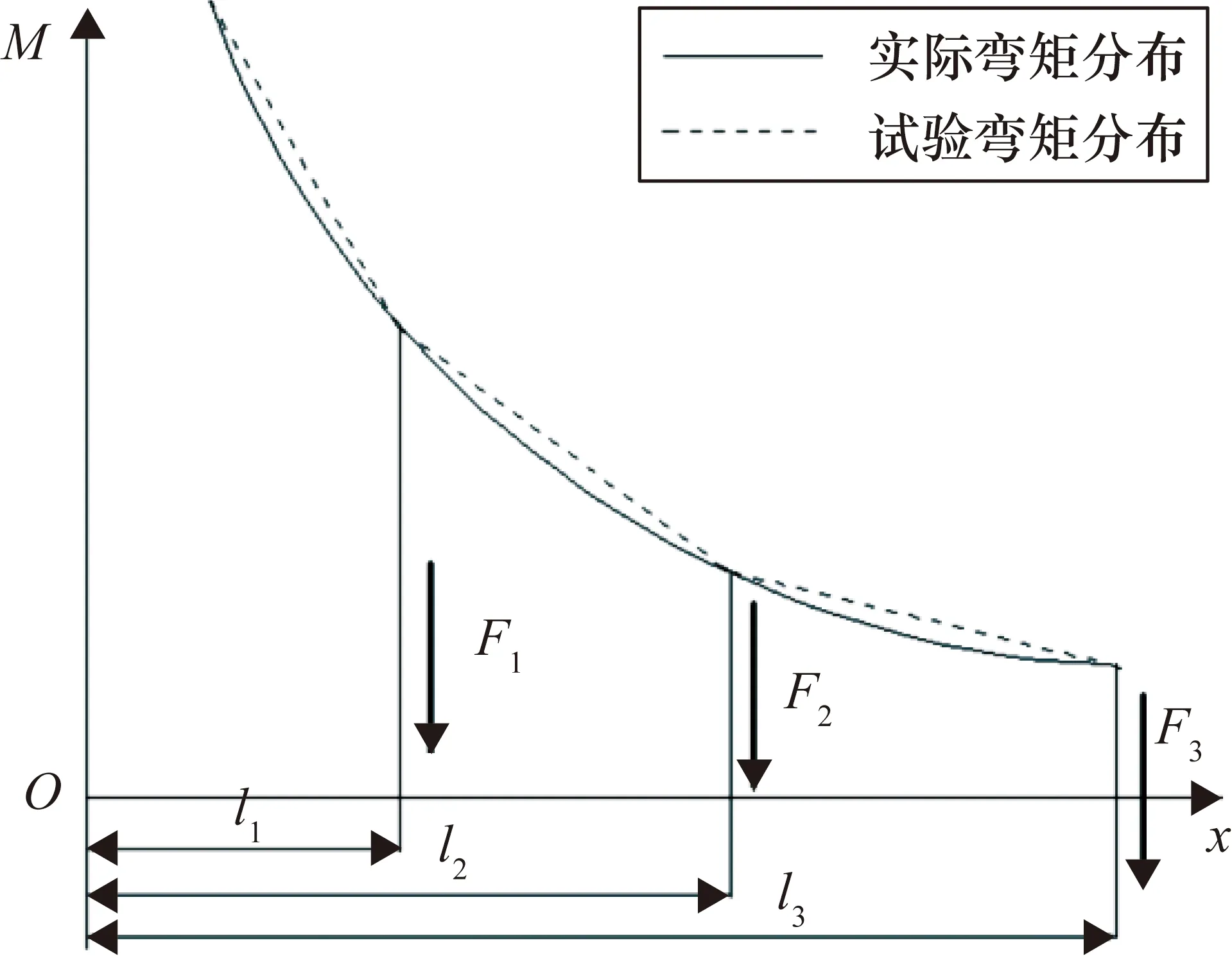
图1 三点静力加载试验与实际弯矩分布示意图

图2 大型风电叶片全尺寸结构静力测试

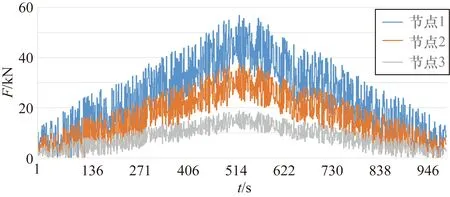
图3 叶片三点静力加载交联耦合曲线

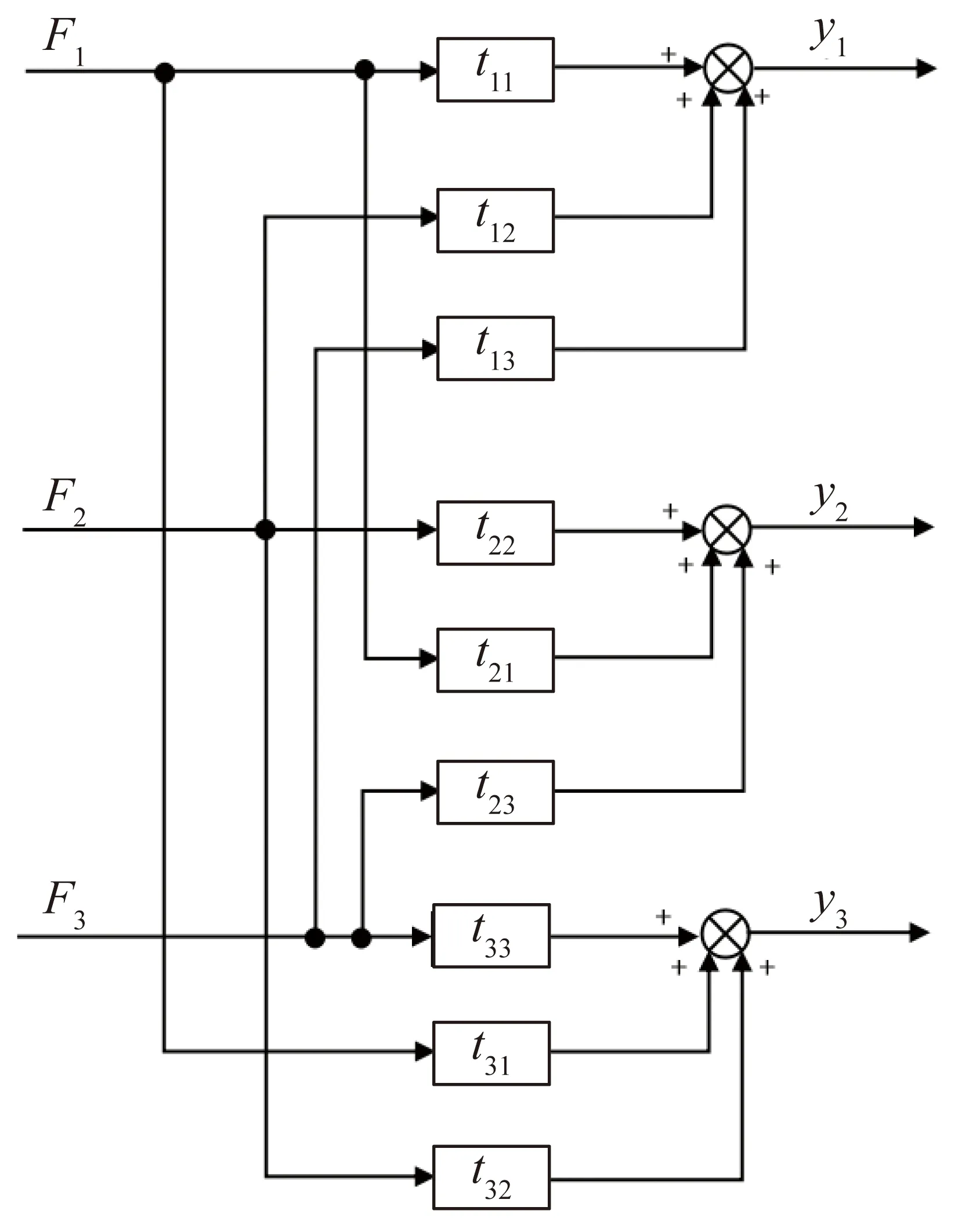
图4 叶片三点静力加载耦合传递关系

根据材料力学理论，叶片单点加载后的挠度变形公式为

(1)

式中，l为加载点距叶根距离；E为叶片的弹性模量；I为加载点界面惯性矩。节点1的挠度等于节点1加载力自身引起的挠度加上节点2和节点3上加载力在节点1处产生的挠度，节点2和节点3类似，各点的挠度变形公式为

(2)

由此可得三点加载耦合传递模型中各节点间的耦合系数tij，节点2与节点1之间的耦合系数计算如下：

(3)

同理可得节点1和节点3以及节点2和节点3之间的耦合系数t13，t31，t23，t32。将上述的载荷耦合传递关系写成矩阵形式[4]为

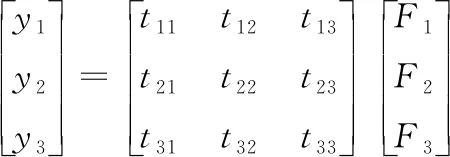
(4)

此矩阵即为该系统的耦合矩阵，表征各节点上的加载力与各节点挠度的耦合传递关系。

2 变步长BP神经网络PID自整定算法

2.1 神经网络PID控制系统

对于叶片多点静力加载这类非线性强耦合的控制系统，PID控制算法很难通过人工调节到合适的参数。同时由于不同的被测叶片其截面刚度等参数不同，因此对控制系统的鲁棒性提出了较高的要求。神经网络PID自整定算法具有较高的适应性和学习能力，利用这一特性能够实现叶片多点静力加载的解耦控制[5]。

控制系统结构分为两部分：神经网络算法和PID控制器[6]，如图5所示。控制器部分选用经典PID控制器，由比例单元(P)、积分单元(I)和微分单元(D)组成。以被控变量的实际值y(t)和期望值r(t)之间的偏差来调节整个系统。

系统偏差：

e(t)=r(t)-y(t)

(5)

控制器输入e(t)和输出u(t)的关系：

(6)

式中，kp为比例系数；TI为积分时间常数；TD为微分时间常数。

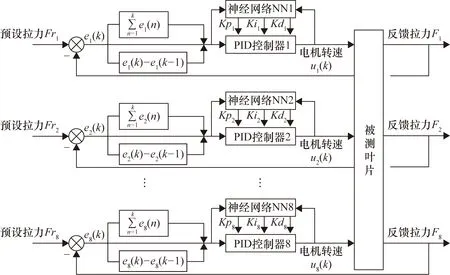
图5 神经网络PID控制系统结构

由于该神经网络应用于非线性的耦合系统，所以初值的选择对于网络能否收敛于预设极小值有很大影响。神经网络初值的选取规则为：输入累加后初始权值能使每个神经元的状态接近零，因此一般选取较小的随机值。本控制系统的神经网络部分初值选择(-0.5，0.5)之间的随机值。

本控制系统采用3×6×3的BP神经网络，输入层包含3个节点，分别为预设拉力与反馈拉力误差e(k)、拉力误差累计之和∑e(k)与误差增量Δe(k)；隐含层包含6个节点，输出层包含3个节点：比例系数Kp、积分系数Ki、微分系数Kd。每一个加载点由一个神经网络控制器控制，所有加载点的神经网络学习算法与PID控制器构成了整个控制系统，神经网络的拓扑结构如图6所示。

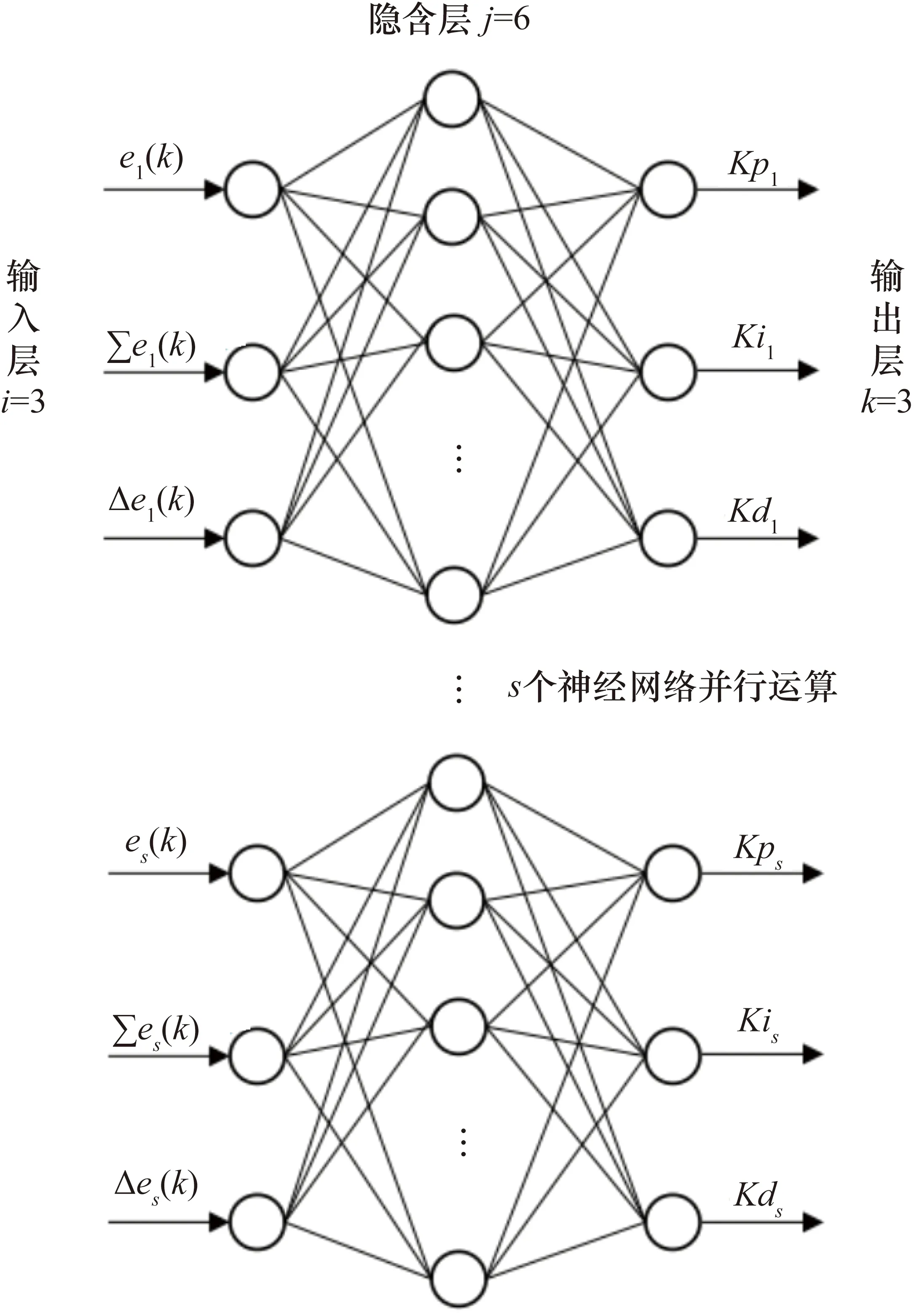
图6 BP神经网络结构图

2.2 变步长BP神经网络控制算法

神经网络具有很强的学习能力，通过分析样本数据中的规律，挖掘输入输出之间的潜在关联，神经网络可以近似拟合任意函数和控制系统[7]。对于耦合系统来说，神经网络无需知晓系统具体的细节，利用其自适应的特性，学习得到合适的控制参数，从而实现解耦控制。

BP神经网络算法由前向传播算法和反向传播算法两部分组成。隐含层和输出层的激活函数都以双曲正切函数为基函数，输出层为保证输出的PID参数非负，故处理为g(x)=0.5(1+tanh(x))。用s代表子网络序号，i，j，k分别表示输入层、隐含层和输出层神经元序号，x和y分别表示输入和输出。在任意时刻t，具体的BP神经网络算法流程分为前向传播、反向传播和变补偿修正算法3个部分。

2.2.1 前向传播算法

(1) 输入层输入输出。

输入层的3个输入分别为拉力误差、误差累计和误差增量：

(7)

(8)

式中，角标(1)表示输入层神经元。

由于3个输入量之间数量级相差较大，因此对其做归一化处理，归一化用非线性的反正切函数：

f0(x)=2arctan(x)/π

(9)

(2) 隐含层输入输出。

隐含层输入为输入层输出与权值乘积之和，经激活函数处理之后得到隐含层输出：

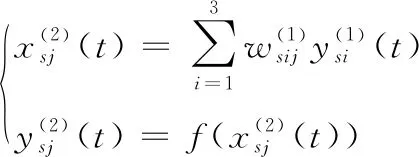
(10)

(3) 输出层输入输出。

输出层输入为隐含层输出与权值乘积之和，经激活函数处理之后得到输出层输出：

(11)

(12)

式中，kp，ki和kd为预设的PID参考值；Kp，Ki和Kd为最终输出给控制器的实际PID参数。

2.2.2 反向传播

通过引入性能指标JS来衡量系统的性能，当指标函数大于预设的系统阈值时，BP神经网络开始反向传播运算，调整各层神经元之间的权值。

性能指标函数JS的计算公式如下[8]：

(13)

式中，n为子网络个数，对于6点同步加载，即n=6；s为子网络序号。反向传播时，按照梯度下降法修正网络连接权值，即按JS对权系数的负梯度方向搜索调整。修正公式中引入变步长修正算法，以提升此BP神经网络的稳定性和收敛速度。

2.2.3 变步长修正算法

经典的BP神经网络权值修正公式为[9]

(14)

式中，η为学习速率；α为惯性项系数，分别与神经网络的收敛速度和稳定性相关。现引入变步长修正算法，对学习速率与惯性项系数分别增加一项系数：

(15)

式中，θ为误差负梯度方向与上一时刻权值修正值的夹角。当θ接近0，即前后两次误差的负梯度方向相近时，学习速率约为2η；当前后两次误差的负梯度方向相反时，θ接近180°，学习速率近似为0。当反向传播的搜索过程较稳定时，可以以较快的学习速率加速收敛，反之神经网络反向搜索出现振荡时，减缓学习速率。

(16)

惯性系数中添加的一项为负梯度与前次修正值范数之比，旨在平衡梯度项与惯性项的比例。梯度项是网络收敛的必要条件，惯性项帮助BP神经网络跳脱局部收敛[10]，两者数量级相差过大，任一项失去作用都会导致控制精度下降。

3 仿真模拟与现场实验结果分析

3.1 算法仿真

仿真中用3个节点进行试验，参考某型58 m叶片，在距叶片根部14.7 m，25 m，45.7 m处进行静力加载。根据叶片各点处截面刚度和惯性矩等参数，构建此叶片的耦合矩阵：

实际的控制系统由PLC输出变频器频率，换算为伺服电机的转速，经由减速器和卷筒，最终牵引缆索对叶片施加拉力。根据此流程，结合各项参数，利用Simulink建立该系统的数学模型，如图7所示。

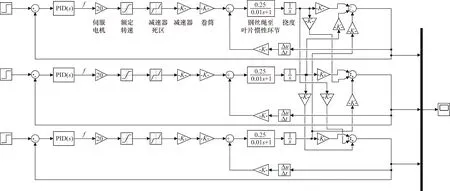
图7 多点静力加载控制系统模型

仿真与实际试验一致，采用分级加载。仿真的控制周期与系统采样周期、神经网络计算周期一致，均为0.5 s。

根据试验要求，3个加载节点预设目标拉力值分别为15 kN，30 kN，45 kN。仿真结果如图8所示。当采用固定PID参数(P=25，I=1，D=0)时，各节点的反馈拉力虽然能跟随预设拉力，但有明显的振荡，说明各节点间存在较强的耦合；利用神经网络自整定PID参数(预设P=25，I=1，D=0)时，各节点不仅能紧跟预设拉力，且几乎没有耦合导致的振荡。仿真系统的稳定性可直接通过性能指标JS来衡量，由JS的计算公式(8)可知，性能指标JS反映了系统预设值与反馈值的差值。固定PID与神经网络自整定下控制效果对比如图9所示，固定PID控制下的性能指标函数JS远大于神经网络自整定控制，而性能指标函数为系统误差的评价指标，即前者在控制精度方面远远不如后者。

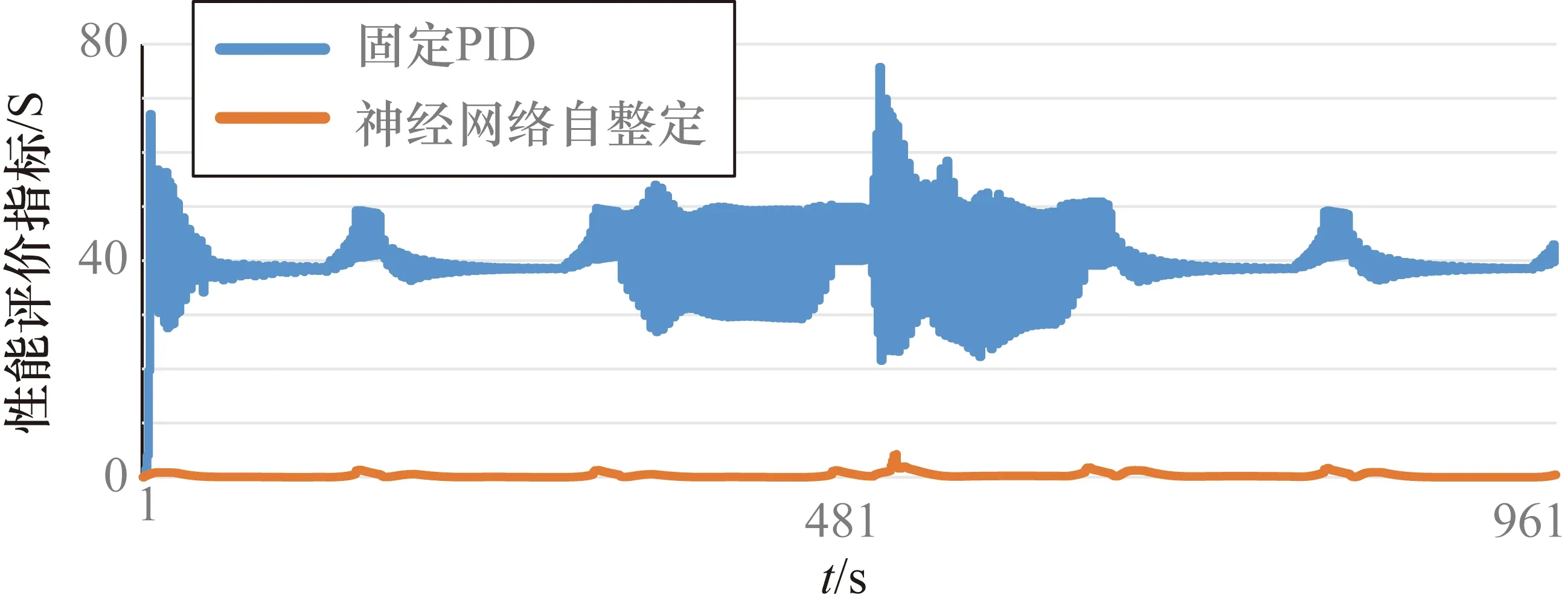
图9 仿真系统稳定性评价对比图

为验证神经网络的自适应能力，现将模型中的各截面刚度放大3倍，模拟不同的叶片刚度对控制系统的影响，仿真结果如图10所示。即使刚度放大了3倍，依然未出现明显的振荡现象，且控制系统仍能很好地跟踪加载拉力。

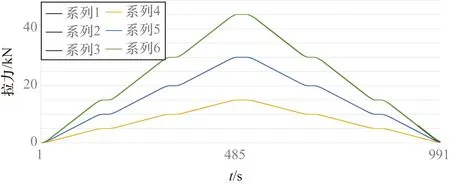
图10 3倍刚度下的反馈拉力

3倍刚度下系统的评价指标如图11所示，可以看到系统整体性能指标与1倍刚度时相差无几，除了在540～600 s，卸载刚开始处误差稍大外，其余时间误差都与1倍刚度时走势相似，甚至略低于1倍刚度时的误差。此结果证明神经网络可以自适应不同叶片加载控制，控制系统有较高的鲁棒性。

图11 不同刚度下系统控制性能对比图

3.2 现场实验

基于上述理论与仿真模型，进行了现场实验。实际加载叶片的截断长度为47 m，分别在距叶根15 m，29 m，34 m，38.5 m，42 m，46 m处进行6点同步加载，最大加载力由实验大纲给出，控制系统网络拓扑关系如图12所示。上位机上的LabVIEW程序控制主控PLC，主控PLC以轮巡的方式通过以太网与若干个从站PLC建立通信。从站PLC负责采集拉力、位移、电机电流等数据并反馈给主站以及控制对应编号的伺服电机驱动器，指挥伺服电机完成各自的虚拟指令。

实际加载拉力曲线如图13所示，由于钢丝绳需要预紧，以及钢丝绳和力传感器的自重，加载开始和结束时的拉力会略大于0 kN。由于测试叶片是试验用旧叶片，且加载方向为Edgewise摆振方向，为避免把叶片拉断，因此目标载荷较小。

从图13中可以看到，各加载力能紧跟目标值且未出现大的振荡或波动，无明显耦合现象；最大加载力保持阶段拉力都能保持在±1%之内。由此可见，BP神经网络能较好地进行解耦控制，且控制精度也比较高。

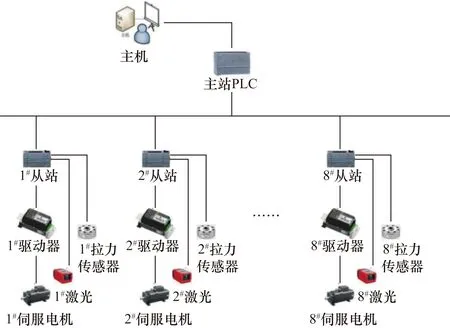
图12 叶片多点静力加载控制网络拓扑图

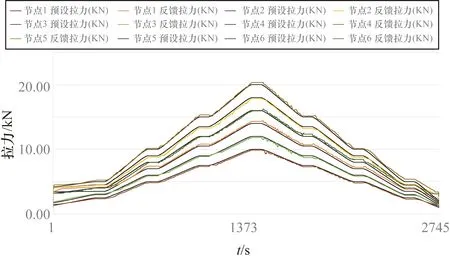
图13 实测拉力曲线图

4 结束语

本文利用神经网络自适应、自学习特性解决风电叶片多点静力加载这类非线性强耦合问题，提出了一种BP神经网络PID自整定算法，神经网络部分引入变步长算法以提高网络的稳定性和收敛速度。通过建立叶片多点加载耦合系统模型和仿真测试证明了神经网络的解耦能力，并在现场试验中验证了BP神经网络控制器的实际控制能力。结果表明控制系统在6点同步加载过程中解耦效果较好、响应快、运行平稳，且具有较高的控制精度。