基于多尺度模糊熵的齿轮故障诊断方法
吴英建, 王景霖, 刘贞报
(1.上海航空测控技术研究所 故障诊断与健康管理技术航空科技重点实验室,上海 201601;2.西北工业大学,陕西 西安 710072)
齿轮箱作为机械设备中传递动力和运动的通用零部件,由于其传动比固定、结构紧凑、传动精度高等优点,已经在金属切削机床、航空、电力系统、农业机械、冶金机械等现代机械设备中得到了广泛的应用[1]。但是由于齿轮箱结构复杂、工作环境恶劣等原因,齿轮箱在机械设备中容易发生故障。尤其在计算机和电子技术快速发展的今天,机械设备不断向大型化、高速化、自动化和智能化方向发展,齿轮箱的故障和失效给生产和社会造成的损失也越来越大[2-3]。
由于齿轮箱在高速、重载、极端工作温度、污染等恶劣工况下,容易受到各种损伤。齿轮箱的意外故障会破坏整个机械系统,造成巨大的经济损失,甚至灾难性的故障[4]。因此,齿轮箱状态监测与故障诊断技术的研究对减少和避免由于零部件故障而引起的整套设备停止工作,由事后维修、定期维修到视情维修的转变和延长齿轮箱服役时间和使用寿命等方面具有积极意义[5]。同时在保证工作人员人身安全、提高维修质量减少平时备件储备、减少不必要经济损失方面也具有重要意义。
在过去的几十年里,人们在利用特征提取和分类方法开发各种故障诊断方面做出了显著的努力[6-7]。一般来说,齿轮箱的故障特征提取方法可以归纳为3个阶段:数据采集、故障特征提取和故障模式识别。在这3个阶段中,齿轮箱的特征提取极为关键,直接决定最终分类结果的好坏。
熵是一种检测时间序列动态变化的指标,在旋转机械的故障诊断中得到了广泛应用[8-9]。健康齿轮箱振动信号的不平稳性较大,熵值较大;故障齿轮箱振动信号的不稳定性较小,熵值较小。首先采用基于多尺度模糊熵(Multiscale Fuzzy Entropy,MFE)的特征提取算法来提取齿轮箱的故障特征;然后将故障特征输入到K最近邻(K-Nearest Neighbor,KNN)分类器中自动识别齿轮箱的健康状态。利用齿轮箱实验台进行齿轮故障模拟实验,设计了实验方案,通过对实验结果进行分析验证振动诊断方法在齿轮箱故障诊断中的有效性,并通过与传统诊断方法的比较验证了基于MFE-KNN方法的有效性,实现了齿轮不同故障类型的定量诊断。
1 多尺度模糊熵分析
由于近似熵和样本熵均采用阶跃函数来定义序列相似性,与实际样本类边缘比较模糊不符,模糊熵被利用模糊函数来定义相似性。模糊熵(Fuzzy Entropy,FE)[10]的详细计算步骤如下所示。
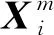
(1)
式中,i=1,2,…,N-(m-1);x0(i)为m个连续x(i)的均值。
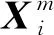
(2)
式中,i≠j,i=1,2,…,(m-1)。
(3)
式中,r为相似容限;n为梯度。
④ 定义函数φm(n,r)表达式如式(4)所示。
(4)
⑤ 维数增加至m+1,重复步骤①~步骤④得到φm+1(n,r)。
(5)
对于时间序列{Xi}={x1,x2,…,xN}的模糊熵定义为
(6)
如果序列长度N为有限数时,FE(m,n,r)可以表示为
FE(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r)
(7)
模糊熵将原始序列映射到高维空间,利用幅值容限内的高维矢量来定义序列复杂度,同时采用模糊函数定义序列相似性,更加符合实际情况。但是模糊熵是从单一尺度上去考虑时间序列复杂度,可能会丢失必要的故障模式识别信息,因此考虑采用多尺度的思想对振动信号提取多尺度模糊熵特征。为了更好地描述时间序列的复杂性,Costa提出了多尺度的概念[11]。多尺度分析的思想如下。
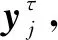
(8)
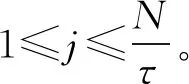

图1 多尺度粗粒化过程
(5)
多尺度模糊熵[12]的参数包括嵌入维数m、相似容限r、模糊函数的梯度n、尺度因子τ。从定义可以看出模糊熵中的嵌入维数m与近似熵和样本熵中一致,重构的维数越多,考虑的细节信息越丰富,但是需要的时间序列越长,不利于提高计算效率,一般情况下取m=2。相似容限r表示的是模糊函数边界的宽度,r太大会引起边界过宽,在进行匹配的时候会引入很多不相似的信息;r变小会增强噪声的敏感性,不能提取到合适有用的序列信息,因此r的取值一般与序列相关,r=0.1~0.25×SD,SD为序列的标准差,这里选择r=0.15×SD。模糊函数梯度n是序列相似性度量权值的决定因素,取n=2。尺度因子τ决定了时间序列粗粒化的分割数量,对计算结果也有较大影响,选择尺度因子τ=10。
为了进行对比分析,还使用了参考文献中的时域和频域指标[13]。与基于熵的方法不同,时域和频域指标检测局部损伤引起的周期性脉冲,各时域和频域指标如表1所示。

表1 时域和频域指标列表
特征提取后,将训练样本作为输入,对分类器进行训练。然后,经过训练的分类器可以利用测试样本自动识别齿轮箱故障类型或严重程度。本文选取KNN分类方法进行分类。KNN分类算法[14]是数据挖掘分类技术中最简单的方法之一。所谓KNN,就是K个最近的邻居的意思,说的是每个样本都可以用它最接近的K个邻居来代表。KNN算法的核心思想是如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN方法在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合[15]。
2 基于MFE和KNN的齿轮箱诊断流程
基于MFE和KNN齿轮箱不同故障位置特征提取方法的步骤如下。
① 采集不同工况下齿轮箱的振动加速度数据,并将其分割成多个样本,且其长度为N=2048;
② 采用MFE提取齿轮箱不同故障类型的特征,得到10个不同尺度下的符号动力学熵值,在本文中,设置嵌入维数m=2,r=0.15SD,梯度n=2;
③ 将样本分为训练集和测试集;
④ 将训练集用来训练KNN模型,并用测试样本输入到训练好的KNN 模型中识别不同的齿轮箱故障类型。
基于MFE和KNN的齿轮箱故障位置特征提取方法流程图如图2所示。
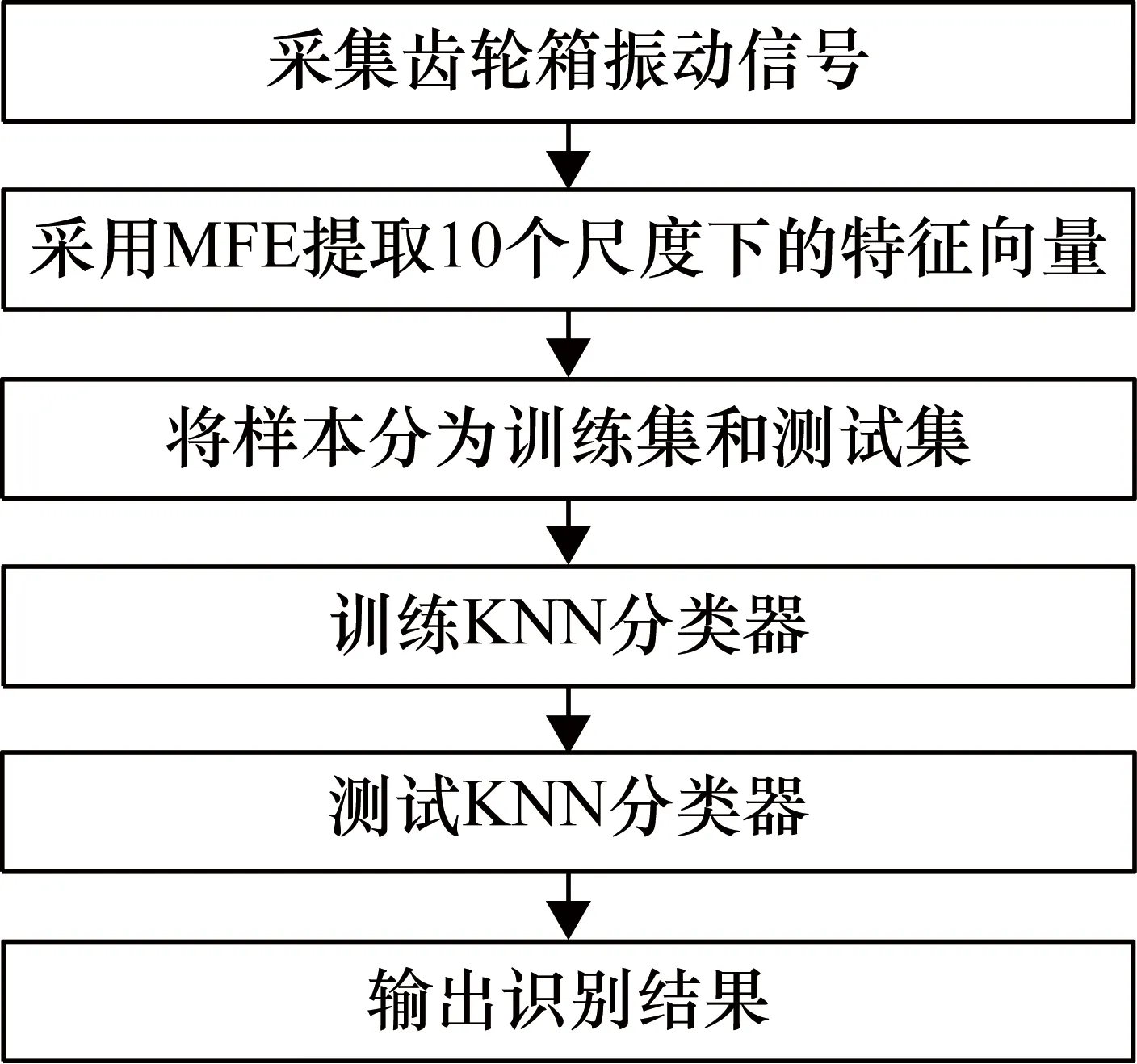
图2 基于MFE和KNN齿轮箱故障位置识别流程图
3 实验验证
3.1 实验装置
在本节中,利用SpectraQuest机械故障模拟器来进行齿轮故障实验,测试平台如图3所示。它由一个可调速电机驱动一个一级直齿锥齿轮的减速器。磁力离合器(也称为负载)安装在变速器的后部。本文中负载为5 in-lbs(1 in-lbs=0.113 N·m)。不同的齿轮故障在故障模拟装置用替换带有预置故障的齿轮来实现(包括主动齿点蚀、主动齿缺齿和从动齿裂纹,实际齿轮故障图如图4所示)。将一个加速度传感器安装在齿轮箱的顶部收集振动信号。采样频率12800 Hz,转速3000 r/min。
3.2 数据集描述
设计了驱动端故障类型识别和驱动端故障严重程度识别实验,将每组实验数据随机分割成100个无重叠样本(样本长度)、50个测试样本和50个训练样本。
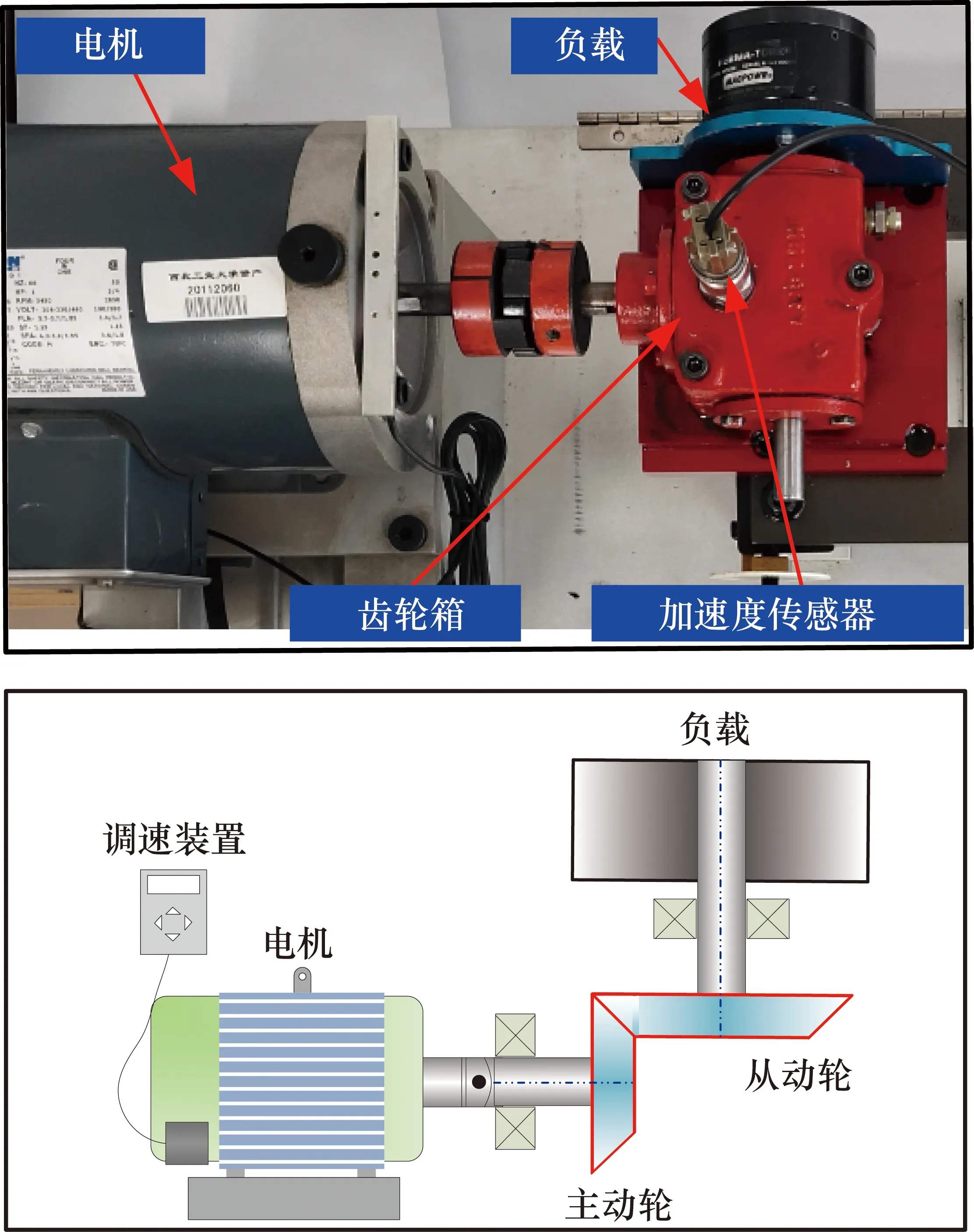
图3 实验系统及其示意图

图4 故障齿轮
在本次实验中,包含了健康状态和5种故障类型:健康、主动齿点蚀、主动齿缺齿、从动齿裂纹、主动齿点蚀从动齿裂纹和主动齿缺齿从动齿裂纹。将每组实验数据随机分割成100个无重叠样本(样本长度)、50个测试样本和50个训练样本。实验中6种故障类型标签如表2所示,其相应的时域波形如图5所示。
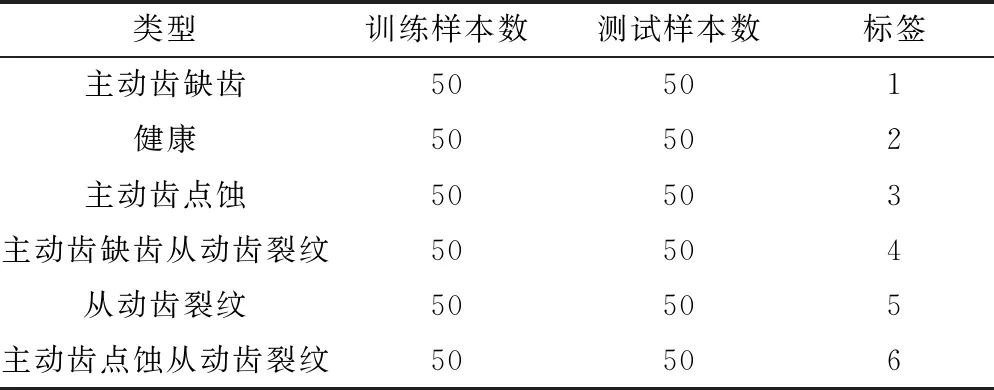
表2 故障类型标签及实验样本数
4 结果与讨论
4.1 实验结果
采集实验数据后,用第2节中的方法进行故障类型识别。首先使用MFE方法提取故障特征,然后将故障特征输入到KNN分类器中,其分类结果如图6所示。
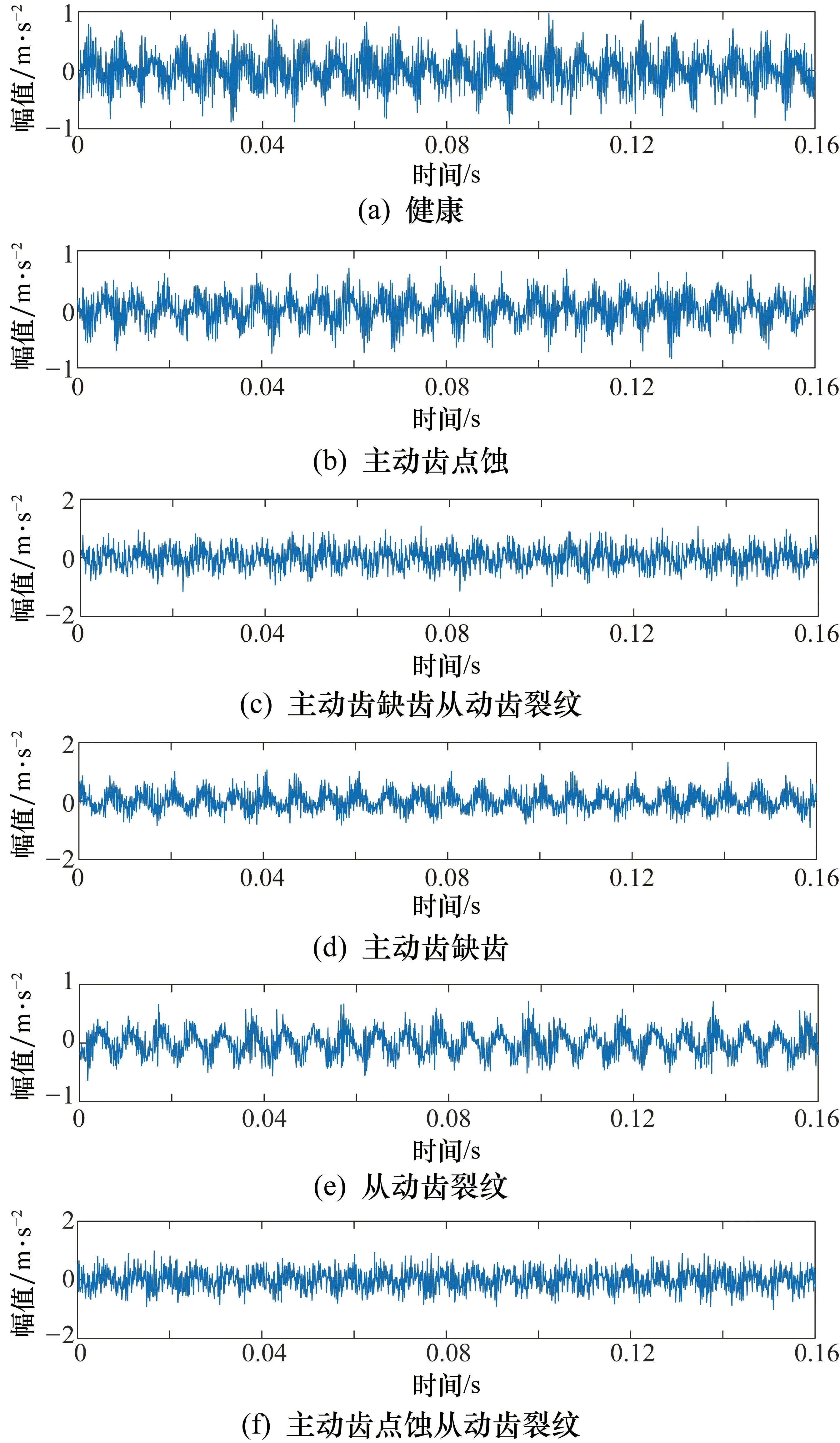
图5 时域波形
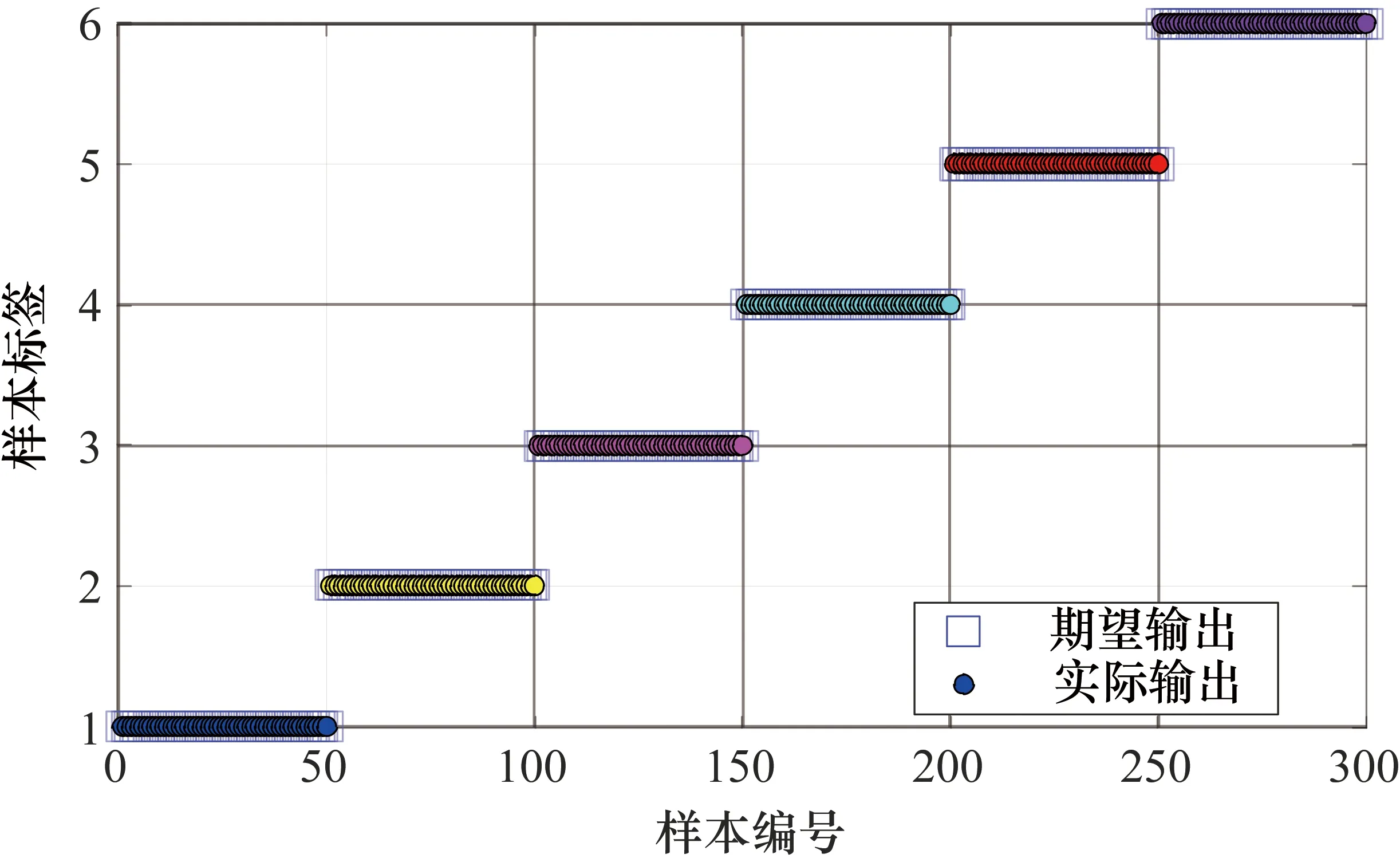
图6 MFE-KNN分类结果
为了减少随机误差带来的影响,将样本测试程序独立运行100次,由图6可以看出最终平均故障类型识别率为100%。为了进行对比验证,分别用多尺度熵(Multiscale Entropy,MSE)和时间与频率特性作为故障特征,然后输入到KNN分类器中,其分类结果分别如图7、图8所示。同样,为了减少随机误差带来的影响,将程序运行100次,如图7所示MSE最终平均故障类型识别率为96%,如图8所示时间和频率特性最终平均故障类型识别率为78%。
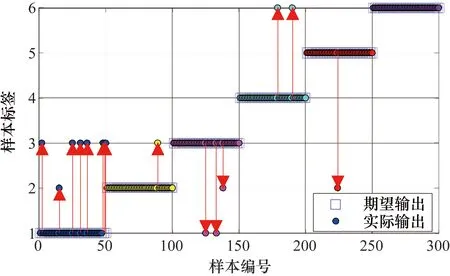
图7 MSE-KNN分类结果

图8 时间和频率特性-KNN分类结果
4.2 讨论
① 通过实验结果发现:MFE方法的故障类型识别率最高,其次为MSE方法,最后为时间和频率特性方法。验证了所提的MFE-KNN方法的有效性。
② 众所周知,齿轮箱局部损伤引起的瞬态脉冲沿长传输路径衰减,淹没在强环境噪声中。数据采集过程中的随机冲击、机械松动和齿轮箱滚动体的随机滑移也会对故障信号产生影响。而MFE方法的优点正是能从强背景噪声中提取故障信息,验证了方法的优越性。
③ 基于熵的方法的优缺点,通过本次实验可以看出MSE和MFE的故障类型识别率较高,优于传统的时间和频率特征提取方法,并且基于熵的方法不需要任何齿轮箱的的先验知识。
5 结束语
提出了一种基于多尺度模糊熵和KNN方法的故障诊断方法。该方法能够从含有强背景噪声的信号中提取故障信息。通过实验比较,该方法优于多尺度样本熵和传统的时间和频域方法,并借助KNN分类器成功识别出5种不同的故障类型,为齿轮故障诊断提供了新思路。

