青藏铁路填土路基热-力耦合离散元研究
石梁宏,李双洋,尹 楠
(1.中国科学院西北生态环境资源研究院冻土工程国家重点实验室,甘肃兰州730000;2.江苏苏邑设计集团有限公司,江苏南京210041)
0 引言
冻土作为一种特殊土类,与其他岩土体最主要的区别是冻土中有冰的存在,而冰的含量又与外界环境温度息息相关[1-4],温度的变化会使得冻土的物理性质、力学性质、电学性质、渗透性质以及其他性质呈现动态变化的特性,这些变化关系着冻土强度和变形等力学以及热学等性能的变化,而冻土又在具有海拔高、气压低、辐射强、稳定性差和局地差异强等特点的青藏高原地区广泛分布[5-7],这势必会使得青藏高原冻土路基工程的热、力稳定性面临更严峻的挑战[8-9]。
为此,可采用不同的路基结构形式或材料,通过调节传导、对流和辐射的传热方式来调控路基温度场,并且在冻土路基温度场的长期热稳定性方面有比较多的研究成果[10-12],较好地解决了青藏铁路建设中可能发生的主要路基病害[13]。而在冻土路基力学变形方面,有限元法、有限差分法、有限体积法等数值计算方法被广泛的应用于冻土路基的热、力学稳定性研究中。其中,王铁行等[14]在土力学弹塑性理论和流变理论的基础上,建立了冻土路基应力及变形的二维数值模型,模拟水、热及土性的动态变化,重点考虑了土性变化情况下土的流变变形和瞬时变形特征;汪双杰等[15]针对青藏公路路基下发育多年冻土融化盘的实际情况,应用ABAQUS有限元分析软件,对冻土路基从修筑到开放交通过程中的路基路面位移及应力进行了分析;许健等[16]以青藏铁路北麓河试验段为计算模型,计算冻土路基的温度场和温度影响下的应力、变形场,并且与实测温度和路基变形数据进行了对比分析;毛雪松等[17]建立了冻土路基变形场的二维数值计算模型,并应用有限元的方法求解路基土体冻结时变形场的分布规律,并进一步分析了冻土路基破坏的机理;李宁等[18]基于正冻土三场耦合的理论框架以及所开发的全面考虑正冻土骨架、冰、水三相介质水、热、力与变形的真正耦合作用的分析系统3G2001,对214国道花石峡试验进行数值研究,并与路基实测的地温变化和路基路面变形进行了对比分析验证;李双洋[19]、Li等[20]以冻土区青藏铁路路基某断面为例,运用传热学、冻土物理学和冻土流变学的基本理论,考虑水分场和温度场的相互作用,以及温度变化对路基土体力学特性的影响,并引入冻土的蠕变方程,建立了冻土路基的热、力学(蠕变)稳定性分析模型,对该段路基运营若干年后的热、力学状况进行了分析和预测。
但是,以上研究都是基于连续介质力学的分析方法,不能充分考虑颗粒之间的导热与接触的相互作用,在分析冻土路基热-力稳定性的破坏变形上也存在瓶颈。为此,可采用颗粒离散单元法进行分析研究,该方法克服了传统有限元法难以模拟冻土路基的大变形与破坏等情况。此外,颗粒离散单元法可模拟颗粒间的导热和点点接触粘结,并从微细观水平反映路基的宏观热、力变化状况。
基于目前冻土路基热-力稳定性研究中存在的不足,本文选取青藏高原五道梁地区某冻土路基断面为例,首先建立随冻土路基温度场变化的热-力耦合离散元计算模型,在验证数值模型正确可靠后,对路基的热、力状况进行预测和分析,并从微细观水平分析冻土路基的宏观变形。本项研究不仅可填补冻土路基离散元研究的空白,而且也拓展了离散单元法在冻土路基工程领域的研究,在理论与实践上都具有很重要的意义,可更好地为寒区工程提供服务。
1 数学模型及方程
1.1 数学传热离散元模型
将物质离散为热源和热通道组成的网络连接体系,从单个热源出发,建立离散化的热量传输方程。单个颗粒的控制体积为V(通常假定所有颗粒的控制体积等于总物质体积),单位体积中热流出量可表示为qi的散度,其平均值定义为

运用高斯散度定理,用面积积分代替体积积分,得

式中:ni为面S的单位法向向量(向外)。
假定离散化的网络连接体系中形成N个热通道,限定热量在N个热通道中流动,则面积积分可用下式表示。
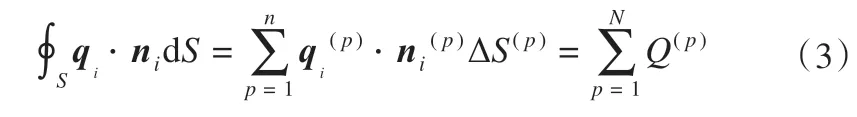
式中:上标(p)为连接通道p的相关变量;Q(p)为在连接通道p中从热源流出的热量,qiΔS(p)=Q(p)ni(p)。
将式(3)和式(2)代入式(1),得到

假定温度对应变变化的影响很小,可以忽略,这个假定应用于涉及到固体和流体的准静态力学问题,则这种连续介质的热传导控制方程为

式中:qv为体积热源强度(W·m-3);ρ为质量密度(kg·m-3);Cv为 质 量 热 容(J·kg-1·℃-1);T为 温度(℃)。
将式(4)代入式(5),得到热传导方程。

1.2 颗粒粘结模型
冻土的力学性质主要取决于土中胶结冰的性质[21],所以在冻土领域运用离散单元法进行仿真研究,需要充分考虑到冻土中冰胶结的重要作用。在离散元法中,可以采用粘结发生在接触颗粒间有限范围内的模型来考虑冻土中冰的胶结特性,这种粘结模型能更好地描述冰的胶结性质,如图1所示的胶结结构[22-23]。取A和B两个颗粒之间的胶结特性进行研究,如图2所示。

图1 冻土中胶结结构示意图[23]Fig.1 Sketch map of the cementation structure in frozen soils[23]
在三维情况下,颗粒间接触的相对运动在胶结连接处会产生力和力矩,作用于相互连接的颗粒上,将颗粒A和B相互接触作用的区域等效为一个圆盘,模型中的接触力和力矩可分解为法向(Fn、Mn)和切向(Fs、Ms)矢量的形式[23]。在平行粘结模型中,法向抗拉强度和切向抗剪强度分别为-σc、-τc,等效圆盘的半径为R,则作用在等效圆盘上的最大拉应力和剪应力的计算方法为

图2 颗粒间的接触模型示意图Fig.2 Sketch map of the contact model between particles

式中:A=πR2,为等效圆盘的面积;I为等效圆盘截面的惯性矩;J为等效圆盘横截面通过接触点的惯性矩。如果-σmax≥-σ或者-τmax≥-τc,则发生粘结破坏。
2 数值计算模型
根据青藏铁路沿线钻探地质资料[24],建立路基实体模型,图3所示。模型中填土路面宽度为7.2 m,填土高度为5 m,路基边坡坡度为1∶1.5。路基模型在坡脚处水平向外各延伸30 m,路基下部土层分为三层:2 m厚的砂土层,6 m厚的粉质黏土层,22 m厚的弱风化岩层。

图3 路基实体模型Fig.3 Physical model of the embankment
图4 为冻土路基离散元数值计算模型图,数值模型的尺寸和各层土质与实体模型一致,外侧采用墙体限制。在实际计算中,考虑到路基几何及边界条件的对称性,故取一半路基作为研究对象。

图4 路基离散元数值计算模型Fig.4 DEM(discrete element method)model of the embankment
考虑全球气候变暖的影响,取青藏高原未来50年平均气温上升2.6℃[25],由于路基上表面温度变化不仅与环境空气有关,而且受到太阳辐射等复杂因素的综合作用,故可根据附面层理论[26],对离散元计算模型的热边界条件进行如下的设定:
天然地表AB和EF的温度按下式变化[27]。

式中:th为时间变量。可通过调整α0来改变初始时刻对应的日期,α0=0对应的初始日期为7月15日。
路基斜坡BC和DE的温度按如下规律变化。

路基顶面CD的温度变化规律为

边界ALKJ和FGHI视为绝热边界,即

底部边界JI为热流边界,热流密度为0.06 W·m-2。
离散元的热学计算需用到5个热学微观参数,即密度ρ、线性热膨胀系数α、质量比热容Cv、导热系数λ(或热阻η)及质量相变潜热Ls,表1中列出了冻土路基离散元数值计算中的微观参数。

表1 路基各介质中的离散元热学微观参数Table 1 DEM thermal microcosmic parameters in the embankment
在计算中,对于含水介质中相变潜热问题采用显热容法进行处理[28],假设模型中含水介质相变发生在温度区间(Tm±ΔT)。当建立等效质量热容时,应考虑温度间隔ΔT的影响,同时假设介质在已冻、未冻时的质量比热容热容Cf和Cu及导热系数λf和λu不取决于温度,此时简化构造出质量比热容和导热系数的表达式[29-30]为

式中:Ls为含水介质单位质量相变潜热;T为一定范围内颗粒温度的平均值。
计算中,颗粒接触刚度与路基温度之间的数学关系是基于冻土室内静三轴试验,考虑温度为路基热-力稳定性的主要影响因素,结合冻土力学、传热学、离散元理论以及冻土相关研究成果等理论而建立起来的[20-21,28,31-33]。路基不同土层颗粒接触刚度与温度之间的数学关系为:


几种不同介质土层的颗粒接触刚度与温度之间的数学关系,其变化规律具有一致性。即在温度为正时,颗粒刚度为常数;温度为负时,颗粒接触刚度随温度的降低而线性增大。
3 结果与分析
3.1 数值模型校核
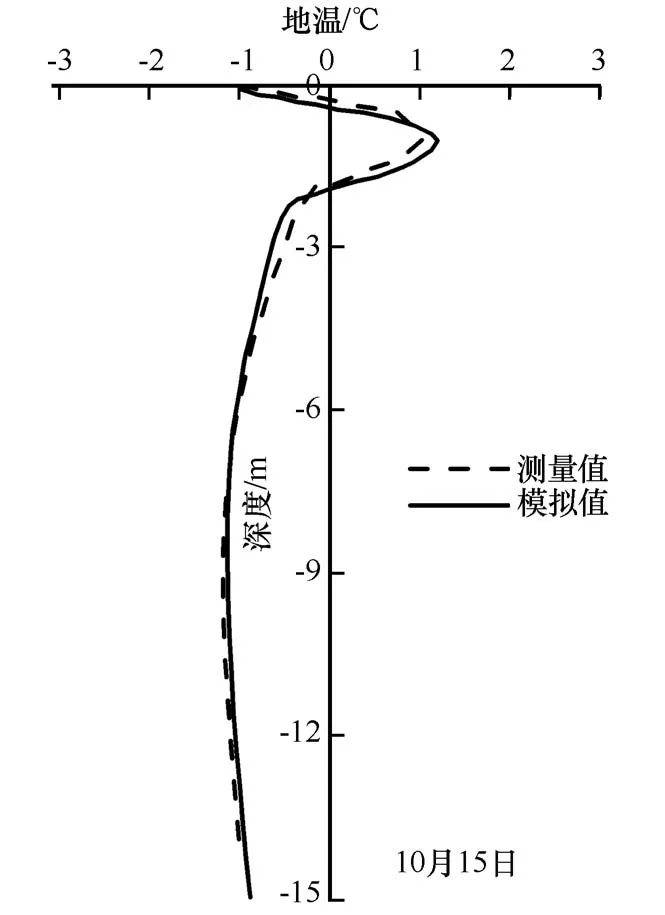
图5 路基天然孔地温变化曲线Fig.5 Ground temperature curves of origin borehole beside the embankment
为了验证离散元数值模型的准确性,将数值模型的计算结果与已有数据进行对比。从图5可以看出,离散元计算的路基天然孔地温曲线与实测结果吻合较好,离散元数值计算的冻土上限(0℃等温线)与实测的冻土上限分别为-1.96 m和-1.89 m,相差仅为0.07 m,在路基天然孔地温曲线整体变化趋势上,两者无较大的差别。因此,冻土路基离散元数值模型能真实地计算冻土路基的热变化,模型的准确性较高。
图6 为路基建成后路肩孔地温曲线的比较,可以看出,离散元数值计算和测量的地温曲线总体比较吻合,但是在0~1 m范围内,可以看出离散元模拟曲线有一个明显的“突出”,可能的原因是:热量在粒间通道中传导,传导的过程需要时间,而路基刚建成时,路基上部结构与天然地表的温度存在差异,天然地表颗粒的温度会影响地表上部一定区域颗粒间的热量传输,导致在天然地表上部1 m范围内产生明显的温度变化,这与真实土颗粒之间在温度变化下的相互作用很相似,也说明了离散元法在颗粒热交换相互作用特性方面的模拟更具真实性。总体来看,所建立的冻土路基热-力耦合离散元数值计算模型能较合理地体现路基中颗粒之间热-力作用的变化特征,能较真实地反映出上部路基及下部基础内颗粒体的热交换作用与温度分布状况。
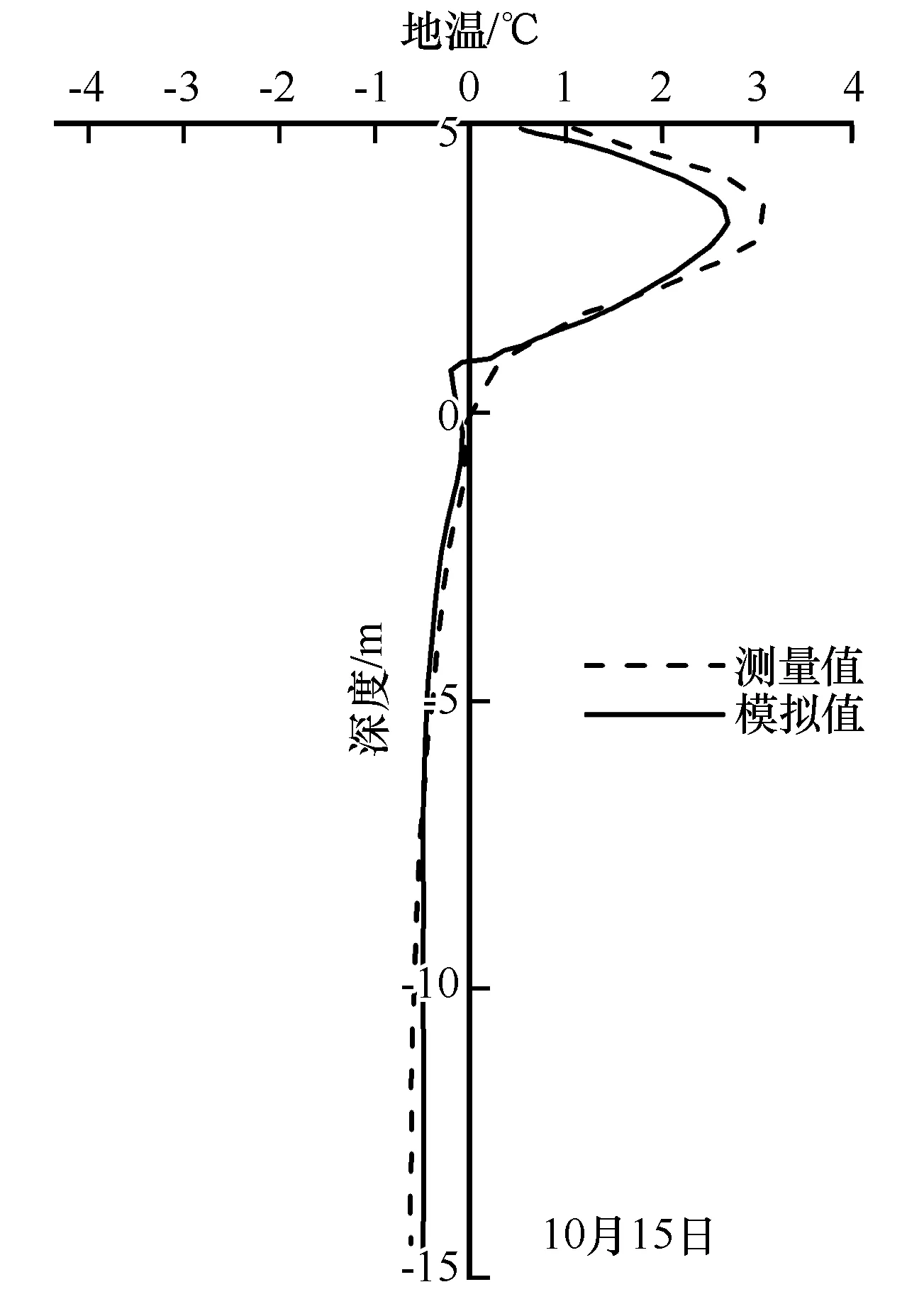
图6 路基路肩孔地温变化曲线(图中天然地表面为纵坐标的原点)Fig.6 Ground temperature curves of shoulder borehole of the embankment(Natural surface is set as the origin of vertical coordinate)
3.2 路基建成第2年的温度场
图7 选取了路基建成后第2年四个典型季节的温度分布图进行分析。从路基等温线变化情况来看,四个季节都形成-0.8℃温度线。从路基融化深度来看,在7月15日,上部路基内融化深度约为2.15 m,而在10月15日,上部路基内融化深度约为3.20 m。
进一步分析来看,在路基顶部、边坡、天然地表周期变化的温度边界以及底部恒定的热流边界作用下,多年冻土区路基中颗粒之间热传导方式形成的温度场,在下部基础内扰动相对较小,相对较稳定;但是在周期温度变化的边界下,路基内温度场扰动性较强,尤其在冻土上限区域,颗粒之间热传导形成的温度场呈现“紊流”状或“岛”状的分布较明显,等温线波动剧烈。这些变化特征也从微观层面说明,在实际冻土路基中土颗粒之间相互作用和热交换过程的复杂性,从而会形成较紊乱的温度场分布,在寒区从事路基工程活动对冻土存在较大的扰动。
3.3 路基建成第20年的温度场
图8 中,为冻土路基修筑完成后第20年四个典型季节的温度场,可见,在这四个典型季节中,-0.8℃温度线已退化,-0.5℃温度线退化也很严重,而且上部路基内融化深度有一定下移,其中,在7月15日融化深度为2.40 m,下移0.30 m;而在10月15日融化深度为3.80 m,下移0.60 m。从图8(d)可知,天然地表下冻土上限为-2.70 m,而第2年10月15日的冻土上限为-2.25 m,下降了0.45 m,路基存在冻土退化的问题。这些离散元研究结果与路基已有的研究结果一致,可以说明,运用离散单元法对多年冻土区路基的热-力耦合数值仿真较合理,也验证了随路基温度场变化的热-力耦合离散元计算模型的准确性,并且颗粒集合体之间的热交换作用特性也较真实体现冻土路基土颗粒的实际变化情况。
进一步分析来看,在路基修筑完成后第20年的温度场仍存在扰动变化特征,其变化规律与第2年的情况类似,但是从路基修筑完成后第20年4月15日温度分布来看,靠近天然地表区域的颗粒体之间热交换作用比较剧烈,形成的温度场变化较复杂,也体现了实际冻土路基长期热稳定性变化过程的复杂性。
3.4 路基变形分析

图7 普通路基建成后第2年的地温分布Fig.7 Distributions of ground temperature of the embankment in four typical seasons in the 2nd service year

图8 路基建成后第20年的地温分布Fig.8 Distributions of ground temperature of the embankment in four typical seasons in the 20th service year

图9 路基建成后第20年10月15日的位移分布Fig.9 Distributions of displacments of the embankment on October 15 in the 20th service year
图9 为多年冻土区路基建成后第20年位移等值线图,选取10月15日的位移场进行分析,其余三个季节的变化规律类似。整体来看,在热-力变化作用下,路基颗粒集合体之间相互接触、摩擦、热交换等作用比较充分,体现在路基位移等值线上,不是平滑的曲线,而是呈现“锯齿状”波动变化的曲线,这也较真实体现出实际冻土路基复杂变化的特征。从图9(a)可以看出,路基坡脚处相当于水平位移正负变化特征的分隔点,坡脚以左,路基水平位移为负,表明上部路基对下部基础向下的压缩作用较强;坡脚以右,路基水平位移为正,表明下部基础内被压缩的颗粒体会向右继续挤压产生变形,基础部分水平向外延伸越远,则水平压缩变形作用对颗粒体的影响作用就越弱。从图9(b)可以看出,一方面,在重力作用下,路基颗粒集合体会发生沉降变形,另一方面,路基修筑完成后,上部路基结构的重量会向下压缩基础内的颗粒体,在坡脚以右,会继续挤压下部基础内的颗粒体,因此,从路基中心位置向右,路基沉降变形量会不断减小,并且,在路基水平向外延伸较远处与下部基础较深处,沉降变形作用会减弱。
图10 为多年冻土区路基建成后第20年10月15日的接触力链分布,其余三个季节变化规律类似。路基中接触力链的粗细可表征路基颗粒间接触力的大小,也能从微细观水平反映出路基的宏观变形特征。可见,在重力作用下,路基形成强力链与弱力链共同发展的体系。上部路基内的颗粒体会向下与向右运动,挤压基础内的颗粒体,在路基坡脚以左,路基中的柱状力链呈现向左的倾斜特征,在路基中心处,柱状力链呈垂直分布,从路基中心至坡脚处,柱状力链向左的倾斜角度逐渐减小,表明了这部分路基中颗粒间挤压作用向右逐渐减弱;在路基坡脚以右,柱状力链向左的倾斜变化特征逐渐消失,形成柱状力链之间交叉分布的特征,体现了在竖向重力作用下路基颗粒间接触力的变化特点。而路基中网状弱力链分布在柱状强力链周围,并与强力链处处连接,对强力链的稳定起辅助作用,从而使路基发生整体变形。还可知,路基中力链的粗细分布不均匀,各向异性很明显,坡脚以左路基各向异性的程度较坡脚以右路基中的大,表明坡脚以左路基中颗粒间相互作用较强烈。

图10 路基建成后第20年10月15日的接触力链分布Fig.10 Distributions of contact force chains of the embankment on October 15 in the 20th service year
4 结论
本文选取青藏高原五道梁地区某路基断面,在考虑冻土路基中复杂的工程状况基础上,采用离散单元法,建立了冻土路基温度场变化的热-力耦合离散元计算模型,预测和分析了路基的热、力分布状况,并从微细观水平阐释了冻土路基宏观变化的复杂性。结论如下:
(1)对比有限单元法和离散单元法可发现,离散单元法突破了连续介质力学中变形条件的限制,可模拟颗粒之间的相互运动,因此能够较真实反映出路基的热、力变化特征,可应用于寒区路基工程的长期稳定性研究。
(2)多年冻土区路基离散元仿真研究表明,随着冻土路基运营时间的增加,冻土上限会发生下移现象,因此路基存在冻土退化的问题。
(3)冻土路基中颗粒之间热交换过程较复杂,在冻土上限(即0℃等温线)区域,温度场呈现“紊流”状或“岛”状分布,扰动较剧烈,能较真实体现实际冻土路基中颗粒之间的相互作用特性和热交换情况。
(4)冻土路基在坡脚以左,颗粒体的相互作用较剧烈,路基(沉降)变形主要发生在路基主体结构及下部基础一定范围内。
本文的研究具有一定的探索性,所选取断面的热边界条件具有对称性,并且未考虑阴阳坡效应和水分的作用,因此还需要对该系统进一步的研究。作为初步研究,可为今后冻土工程的稳定性研究和寒区工程的建设提供科学依据。

