不规则波与顺流相互作用的数值模拟与不确定度分析

姚 顺，马 宁，丁俊杰，顾解忡

(上海交通大学 海洋工程国家重点实验室；船舶海洋与建筑工程学院，上海 200240)

随机不规则波浪和水流广泛存在于实际海洋环境中，波流相互作用极其常见.携带大量能量的海流使波浪要素发生变形，进而导致海域海况趋于复杂与危险.近年来，由波流相互作用引起的船舶失事、海洋结构物毁坏等事故时有发生，因此，研究波流的相互作用，特别是不规则波与流的相互作用具有重要的现实意义.

Tayfun等[1]依据Gram-Charlier(GC)模型给出加入四阶联合累积量修正的GC分布，研究了非线性对不规则波的波高概率分布的影响.Soltanpour等[2]和Wei等[3]通过一系列实验分别研究了波流相互作用下波浪在泥床上的耗散情况和目标桥梁基础与上部结构的水动力响应特性.Jiang等[4]和Liu等[5]利用计算流体力学(CFD)软件建立数值波浪水池，模拟了规则波、不规则波与淹没式防波堤及半潜式圆柱体的相互作用，并将模拟结果与实验结果进行对比，研究结果表明不同波参数的入射波对波浪与结构物的相互作用影响显著.Dong[6]建立了一套新理论用于描述有限水深条件下，强剪切流作用时的波流相互作用现象，然后用3个实际案例对计算结果进行验证，获得了强剪切流作用下目标波浪的波浪特性.但文献[2-6]对比试验数据与数值模拟结果进行验证的方法从本质上说是定性的.为了定量评价CFD数值模拟结果的可靠性，CFD不确定度分析逐渐受到学者的关注.Zhu等[7]和Deng等[8]分别对船模横摇运动和小水线面双体船在波浪中的纵向运动进行了数值模拟与不确定度分析.Bachynski等[9]对单桩海上风电机组在不规则波作用下的响应进行了数值模拟，并对波面高度和单桩弯矩的数值模拟结果进行了不确定度分析.Coe等[10]和Bai等[11]则分别对波浪能转换器的线性动力学模型和聚焦波波面升高时历结果进行了不确定度分析.然而文献[7-11]并没有进行波流相互作用模型的不确定度分析，水流对计算结果不确定度的影响研究更是鲜有出现.该问题的难点在于开展波流相互作用试验时很难保证造波精度.丁俊杰等[12]对上海交通大学风洞循环水槽的消波装置进行了改进，改进后该水槽能满足不规则波与顺流相互作用的试验要求.由于水槽造波设备的限制，逆流中的造波实验暂未实施，虽然逆流中的波浪具有更强的非线性和不稳定性，但顺流条件是大多海洋结构物设计的基本要求条件，所以本文将聚焦于顺流条件下的波浪生成、波流相互作用及不确定度分析.

本文开展均匀流与不规则波相互作用的物理试验，基于雷诺平均Navier-Stokes(RANS)方程建立数值波浪水池，求解不规则波与均匀流相互作用问题.对有义波高、平均周期的计算结果开展不确定度分析，并详细探讨了均匀流对不规则波的运动学及能量特性的影响情况.通过不确定度分析对顺流作用下的不规则波模型进行验证，最后得出顺流对计算结果不确定度的影响规律.

1 试验安排

波流相互作用试验的目的是获取不同工况下指定位置处不规则波的波高时历曲线.试验布置如图1所示，其中vC为流速.试验使用的设备包括：循环水槽、造波机、消波装置、流速计、浪高仪及高清摄像机等.造波机为一台摇摆式造波机，两侧紧贴水槽槽壁，设定造波板振幅和周期后即可生成规则波、JONSWAP谱不规则波与聚焦波等波浪.消波装置是一种多层变角度开孔折弯板透水消波装置[13]，放置在距造波端6 m处，能够保证较高的透水和消波效率.采用毕托管测量水流流速，其原理是通过流体压力与静压力之间的压差来计算流速.浪高仪为电容式浪高仪，量程为300 mm，解析度为0.05 mm，最大采样频率为100 Hz.试验共布置5个浪高仪，1#、2#和3#浪高仪布置在消波装置前侧，分别距造波端3.2、3.6、4.0 m，且分别距水槽左端1.0、2.0、1.5 m；4#和5#浪高仪沿y方向平行放置于消波装置后侧，距造波端6.7 m，且分别距左侧槽壁1.0、2.0 m.

图1 波流相互作用试验布置Fig.1 Arrangement of wave-current interaction test

2 数值模型与试验验证

2.1 数值模型

在计算流体力学商业软件STAR-CCM+中建立数值波浪水池对不规则波与流相互作用问题进行求解，求解过程参考文献[14].该软件采用有限体积法求解，湍流模型选择RANS方程，可表示为

(1)

(2)

μt为湍流黏度；τij为Kronecker函数；k为湍动能.可采用Renormalization-Group(RNG)k-ε模型求解湍流黏度和湍动能，进而获得Reynolds应力.

基于物理水槽在STAR-CCM+中构造二维数值波浪水池，水池的长宽高分别为8.0、0.1、2.0 m，水深为1.6 m.为简单起见，选择源项造波法造波，造波起点与坐标原点重合，x轴正向为波浪传播方向；采用软件库函数Current设定水体速度以实现稳定造流.在尾部2 m处添加阻尼消波段，其主要原理与参数参考文献[15].根据试验中使用的多层变角度开孔折弯板透水消波装置[13]等比例建模，并将消波装置放置在阻尼消波段左侧以达到消波目的.空间离散采用二阶迎风格式，压力和速度耦合求解采用SIMPLE算法.

为保证模拟精度，x、y、z方向对应的最小网格尺寸分别为0.01、0.1、0.0015 m，时间步长为0.001 s，满足x方向最小网格尺度不大于1/100波长，z方向最小网格尺度不大于1/20波高，时间步长不大于1/1200周期的要求[12].自由液面捕捉采用流体体积(VOF)法.数值波浪水池如图2所示，其中，AC和BD边界分别选择速度入口和压力出口，AB边界为无滑移固壁边界，CD边界为速度入口边界，两侧边界选用对称边界.

图2 数值波浪水池Fig.2 Numerical wave flume

本文不规则波的模拟选择目前广泛使用的JONSWAP谱.JONSWAP谱可采用有义波高和谱峰周期表征其能量谱密度，可表示为

(3)

式中：H1/3为有义波高；Tp为谱峰周期；ω为波浪圆频率；γ为谱峰提升因子，此处取3.3；α为无因次参数，此处取 0.049 7；ψ为峰形参数.ωp为ω对应的谱峰圆频率，当ω≤ωp时，取ψ=0.07；当ω>ωp时，取ψ=0.09.

波流相互作用试验与数值模拟工况如表1所示，其中：TES和NUM分别表示对该工况进行试验或数值模拟.每组试验或模拟时长为200 s(约150个波浪周期).每个工况重复3组，通过试验或数值模拟获得自由液面处波高时历曲线后，计算出有义波高和所有波浪周期求平均后的平均周期，然后通过快速Fourier变换(FFT)求取能量谱密度函数(下文称能量谱)以及谱峰周期等波参数，作为该工况的统计数据.为表述方便，下文将工况(F)1(vC=0 m/s)称为无流工况，F2(vC=0.3 m/s)称为顺流工况，F3～F5(vC=-0.1、-0.2、-0.3 m/s)称为逆流工况.

表1 波流相互作用试验与数值模拟工况Tab.1 Test and numerical conditions of wave-current interaction

2.2 试验验证

在x=4 m自由液面处，F1和F2中测得的能量谱密度函数曲线如图3所示.由图3可知，由F1和F2数值模拟获得的H1/3、Tp、能量谱峰值等谱形参数与理论值和试验值相差不大.当vC=0 m/s时，数值模拟得到的能量谱曲线低频部分与目标谱吻合，且曲线光顺；高频段(5～6 rad/s)的部分曲线存在尖劈，说明自由液面存在一定的非线性现象.当vC=0.3 m/s时，数值模拟得到的Tp略小于试验值而H1/3和能量谱峰值略大于试验值，这是由于数值模型的造波方法为源项造波法，没有考虑实际造波机与水流的相互作用影响导致的.

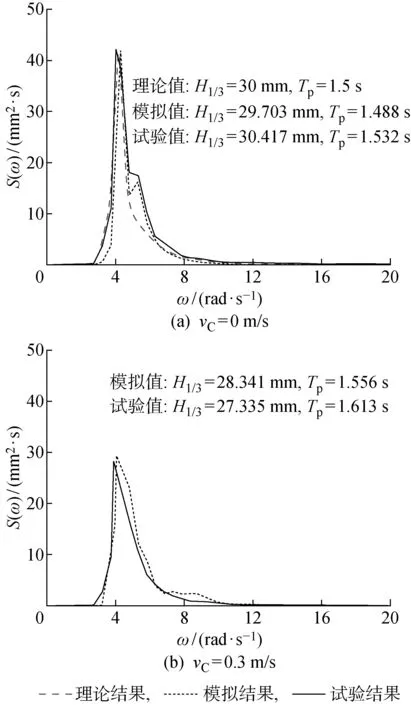
图3 不同流速下的能量谱曲线对比Fig.3 Comparison of energy spectrums at different current velocities

3 数值模拟结果及不确定度分析

3.1 结果分析

偏度Sk是描述波高概率密度曲线相对于平均值不对称程度的特征参数，可以反映波浪的二阶非线性特征，由下式计算：

(4)

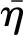
(5)

式中：H为波高；m0为波浪频谱的零阶矩.在深水条件下，Tayfun等[1]推导出GC级数形式的GC分布，在波高为两倍波幅的假设下，波高概率分布为

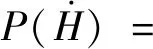
(6)

不同流速下不规则波的有义波高、谱峰周期、偏度值的数值结果及波高概率分布曲线的模拟值与试验值如图4所示，尾部极端值表征波高极大值.由图4可知，顺流时不规则波的有义波高和偏度值小于无流工况的结果，谱峰周期的变化规律则相反，顺流的作用导致谱峰周期有所增大.F1和F2的波高概率分布曲线模拟结果与试验结果比较一致；由F1和F2试验获得的波高极大值略小于数值模拟结果，这一误差同样是由于试验过程中造波机与水流的相互作用导致了造波效率下降所引起的.进一步分析可知，当vC=0、0.3 m/s时，除了尾部的极端值以外，波高概率分布比较符合Rayleigh分布而远离GC分布，不规则波的非线性程度较小；由模拟得到的概率分布尾部极端值从1.32H1/3(vC=0 m/s)减小到1.30H1/3(vC=0.3 m/s)，可见顺流作用下可能的极端波高相对无流情况有所减小.

图4 不同流速下波浪要素与波高概率分布Fig.4 Wave elements and wave height probability distributions at different current velocities

Bitner-Gregersen等[16]利用非线性波浪理论的高阶谱方法(HOSM)研究了无流情况下采样变异性对Pierson-Moskowitz谱和JONSWAP谱不规则波的偏度和峰度等非线性特征的影响情况.上述偏度值计算结果与文献[16]的结果对比如图5所示，其中：波陡ε=σpH1/3/2，σp为谱峰周期Tp对应的波数.由图5可知，相对小波陡的不规则波对应的偏度较小，文献[16]的结果中大波陡不规则波则对应着更大的偏度，进行数据分析可得两者的相关系数为0.996，即偏度与波陡存在明显的正相关关系.在不考虑采样变异性时，逆流的存在导致波陡和偏度值变大.在波浪被阻隔前，逆流能够加剧不规则波的二阶非线性.

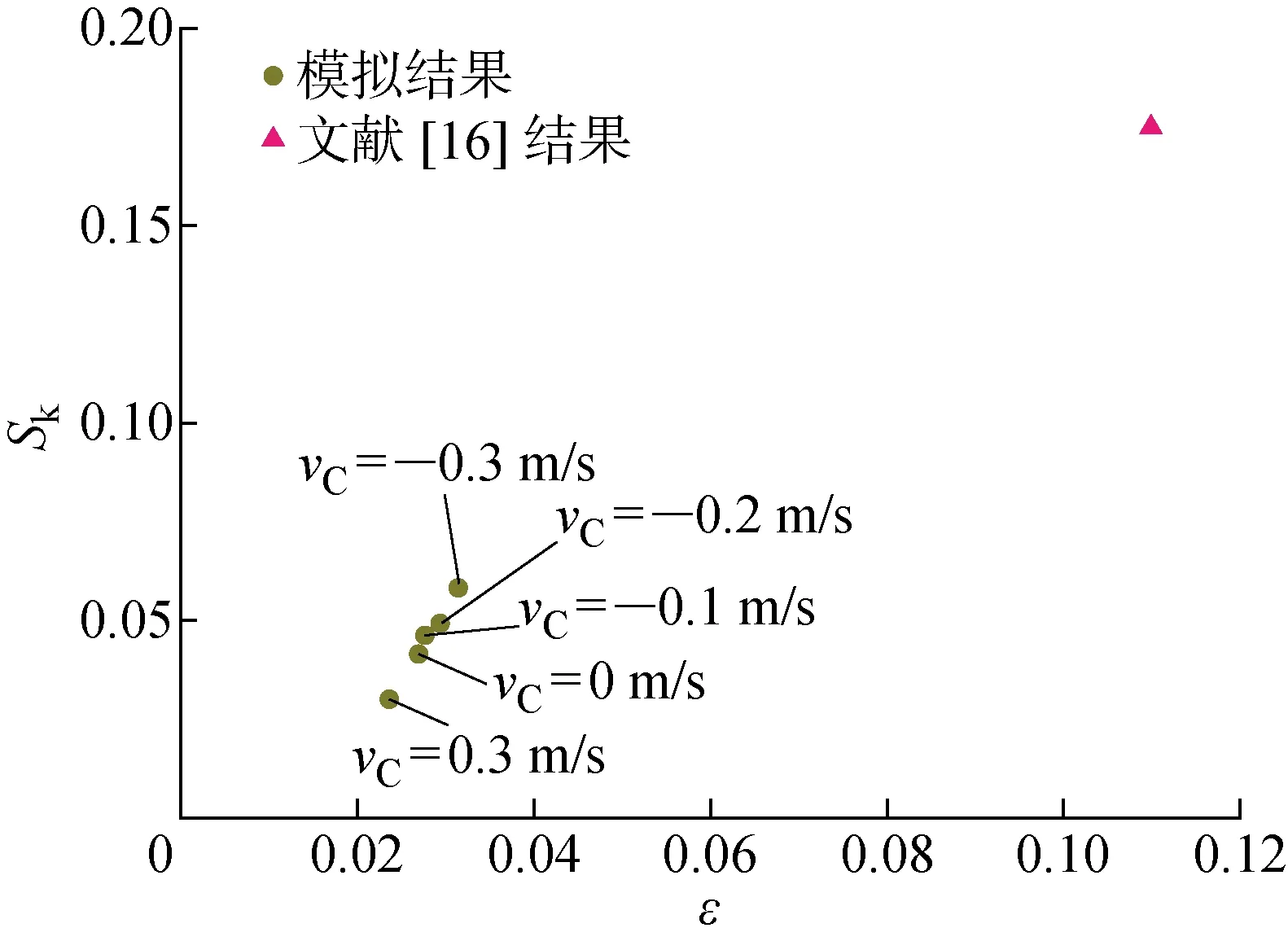
图5 偏度与波陡的关系Fig.5 Skewness versus wave steepness

当vC=0.3 m/s和vC=0 m/s时，流场涡量随时间t的变化示意图如图6和7所示.其中：Ωj为xj方向的流场涡量；箭头表示流场旋涡的传播过程.比较图6和7可发现，顺流流场比无流流场有更大的涡量扩散.结合图4可知，顺流流场涡量增大的同时也导致波浪的有义波高和谱峰频率有所减小.

图6 vC=0.3 m/s时流场涡量示意图Fig.6 Diagram of vorticity of flow fields at vC=0.3 m/s

图7 vC=0 m/s时流场涡量示意图Fig.7 Diagram of vorticity of flow fields at vC=0 m/s

各个工况最大波峰处波高时历曲线及其对应的沿z方向分布的水平速度剖面如图8所示，阴影部分标出了采样时间内的最大波峰-波谷范围.由图8可知，顺流时波峰处水平速度大于无流工况且为正值，意味着波峰处水质点向前运动带动波形向前传播；顺流时不规则波水线面以上的水平速度增长较快，在水线面以下的增长放缓，说明顺流作用更显著地体现在水线面以上的波浪部分.

图8 最大波峰处波高时历曲线与速度剖面Fig.8 Wave elevations and velocity profiles at the largest crest

波浪能量谱能揭示均匀流对不规则波能量特性的影响规律，顺流、无流及逆流情况下不规则波能量谱的数值结果如图9所示.由图9(a)可知，顺流时不规则波能量谱峰值最小，无流次之，逆流最大，这体现了逆流能量的输入.由图9(b)可知，随着逆流流速的增大，谱峰圆频率不断增大，部分能量从低频向高频转移，能量谱谱峰逐渐向高频区域移动.这也符合研究人员得出的水流对不规则波影响的结论[17-18].

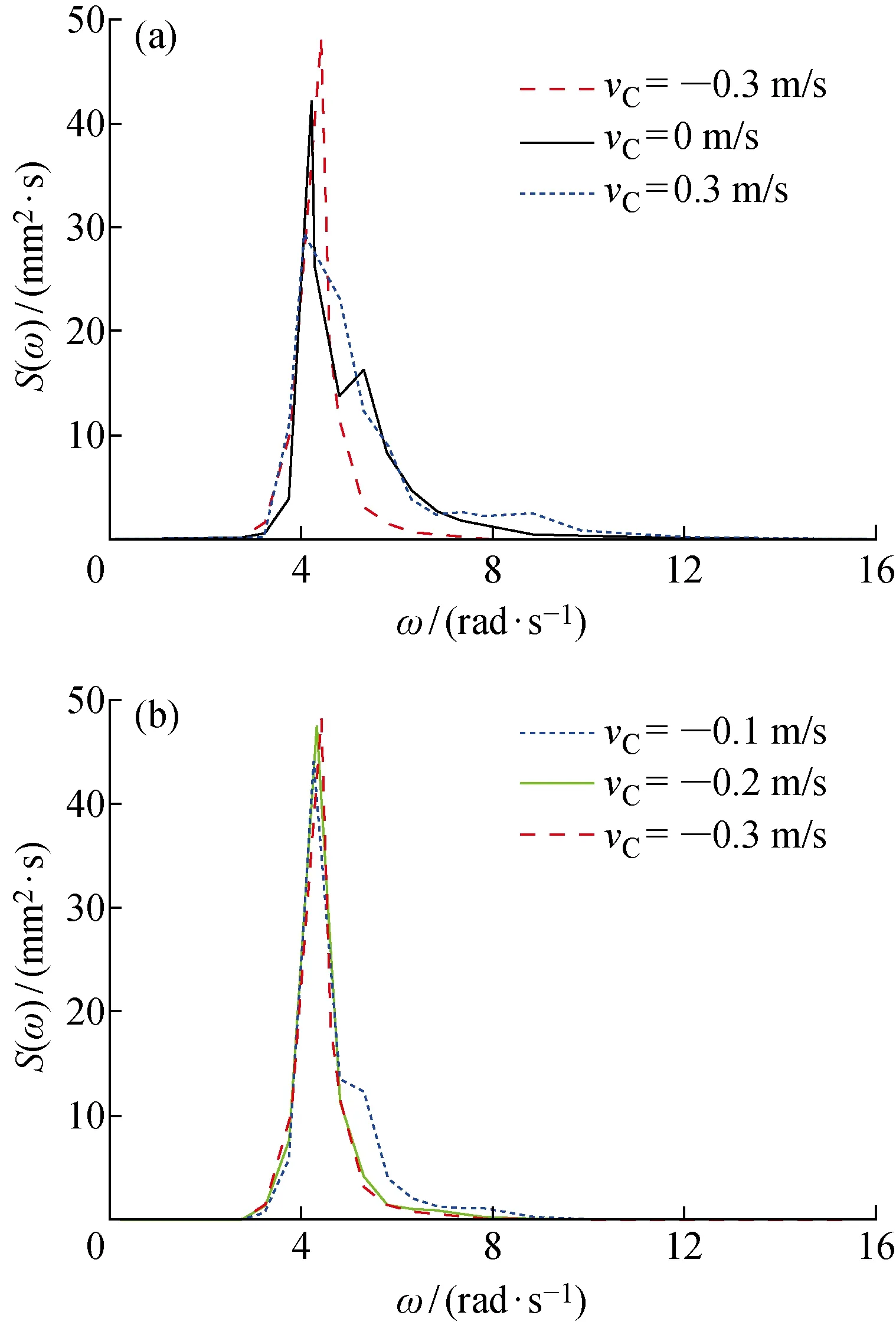
图9 不同流速下不规则波能量谱对比Fig.9 Comparison of irregular wave energy spectrums at different current velocities

3.2 不确定度分析

在试验和数值模拟的基础上，依照国际船模拖曳水池会议(ITTC)推荐的规程对不规则波与顺流相互作用的数值模拟结果进行不确定度分析.不确定度分析主要包括两个方面：验证与确认.验证是评估数值的不确定性，本质是分析“是否正确的求解方程”.确认则是评估模型的不确定度，实质是分析“是否求解了正确的方程”.其中，验证主要包括数值解的多重收敛研究，包括网格收敛性、空间收敛性、时间收敛性、迭代次数和敏感参数收敛性等研究.不规则波与流相互作用属于非稳态问题，数值模拟中网格尺寸和时间步长大小引起的误差远大于迭代步数等其他参数导致的误差，因此将这两个参数作为主要影响因素进行分析.

表2 3套网格下的有义波高值Tab.2 Results of significant wave height of three sets of grid sizes

从表2可以计算出相邻网格G1和G2、G2和G3有义波高模拟值之差的平均L2范数βG21与βG32:

‖βG21‖2=‖HG2-HG1‖2

(7)

‖βG32‖2=‖HG3-HG2‖2

(8)

式中：HGl(l=1,2,3)分别为G1、G2和G3的有义波高数值模拟结果.全局收敛因子RG定义为

〈RG〉=‖βG21‖2/‖βG32‖2=0.425

(9)

实际应用中〈RG〉恒为非负值，网格参数收敛情况可分为两种：① 单调收敛，0<〈RG〉<1；② 发散，〈RG〉>1.

(10)

(11)

网格修正因子CG为

(12)

式中：网格尺寸趋于0，CG接近1时，首项准确度极限阶数估计值AG,est=2.

当|1-CG|<0.125时，网格尺寸引起的数值模拟不确定度UG为

(13)

当|1-CG|≥0.125时，网格尺寸引起的数值模拟不确定度为

(14)

因此，工况1网格尺寸引起的数值模拟不确定度UG=5.93%H1/3,F1，H1/3,F1为F1测得的有义波高试验值.

(15)

同理，进行时间步长收敛性分析前，先获得不同时间步长对应的x=4 m自由液面处的波高时历曲线、有义波高和平均周期，其中有义波高模拟值与试验值如表3所示.

表3 3套时间步长下的有义波高值Tab.3 Results of significant wave height of three sets of time step sizes

依据前文的网格收敛性分析，将与网格尺寸相关的参数修改为与时间步长相关的参数，对时间步长进行收敛性分析，所获得的时间步长引起的数值模拟不确定度UT为

3.47%H1/3,F1

(16)

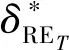
(17)

数值模拟不确定度USN为

(18)

(19)

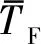
由表4可知，在有义波高的验证过程中当vC=0 m/s及vC=0.3 m/s时，网格尺寸不确定度均大于时间步长不确定度，可见有义波高对网格尺寸的大小更为敏感.vC=0 m/s时的时间步长不确定度明显大于vC=0.3 m/s时的时间步长不确定度，说明顺流降低了有义波高模拟结果对时间步长的依赖程度.由表5可知，平均周期验证过程中当vC=0 m/s及vC=0.3 m/s时，时间步长不确定度均大于网格不确定度，可见平均周期对于时间步长的大小更为敏感.因此，在研究顺流中不规则波的平均周期时，在计算资源有限的情况下应尽量满足时间步长的精度要求.顺流时网格及时间步长的不确定度均大于无流时的计算结果，说明顺流加剧了平均周期模拟结果对网格及时间步长的依赖程度.

在表4中，有义波高在F1下的网格不确定度接近6%，数值模拟不确定度达到6.87%，这是由于网格G3较粗糙，导致的误差较大.为了改善网格的迭代收敛性，可布置更加精细的网格进行计算.

表4 有义波高模拟结果的验证Tab.4 Verification of simulation results of significant wave height

表5 平均周期模拟结果的验证Tab.5 Verification of simulation results of average period

3.2.2确认 对数值模拟结果进行确认，同样以F1的有义波高为例，确认不确定度UV为

(20)

式中：UD为有义波高试验值的不确定度，此处取为2.5%H1/3,F1.模拟值与试验值比较误差的二范数E为

E=‖H1/3,F1-H1/3,N1‖2=2.35%H1/3,F1

(21)

式中：H1/3,N1为工况1数值模拟的有义波高值.可见UV>E，由F1数值模拟得到的有义波高在7.32%H1/3,F1的水平上实现确认.

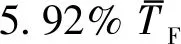
表6 有义波高模拟结果的确认Tab.6 Validation of simulation results of significant wave height

表7 平均周期模拟结果的确认Tab.7 Validation of simulation results of average period

综上，本文基于RANS方程和VOF方法建立的不规则波与顺流相互作用数值模型在求解不规则波有义波高和平均周期时具有可靠性.

4 结论

(1) 顺流及无流时不规则波的波高概率分布符合Rayleigh分布；与无流情况相比，顺流时不规则波的谱峰周期增加，有义波高和偏度值则减小，可能的极端波高也有所减小.

(2) 顺流时波峰处水质点水平速度大于无流时的计算结果，并且顺流流场比无流流场有更大的涡量扩散.

(3) 不规则波与顺流相互作用时，有义波高对网格尺寸更加敏感，顺流能降低有义波高对时间步长的依赖程度；平均周期则更依赖于时间步长，顺流作用下平均周期对网格及时间步长的依赖程度加剧，考虑顺流时的不规则波平均周期时，在计算资源有限的情况下应尽量满足时间步长的精度要求.

(4) 顺流及无流时不规则波有义波高和平均周期计算结果皆得到确认，不规则波与顺流相互作用的数值模型具有可靠性.

由于水槽造波系统设备的局限性，本文研究未能开展逆流中的实验验证，今后拟研发循环水槽逆流中造波(包括消波)技术，开展逆流与不规则波相互作用的不确定度分析的相关试验与数值研究.

致谢感谢上海交通大学循环水槽实验室的支持及代燚、王飞老师对试验的帮助.