变容二极管调频电路参数的高精度测量实验

曾丽蓉，姜乃卓，董英雷，葛中芹

（南京大学 电子科学与工程学院，江苏 南京 210023）

1 问题的提出

高频电路实验目前是很多高校电子信息类专业的主干实验课程，该课程的基础实验部分通常安排若干单元电路模块实验，通过观察电路中某些关键节点的波形和频谱，测量一些重要的电路性能指标参数，促进学生对理论课程中相关重要知识点和典型电路工作原理的理解和掌握[1]。频率调制是无线电模拟通信的一种重要方式，也是高频电路理论课重点讲解的内容，实际电路产生调频信号通常有直接调频和间接调频两种方案。直接调频是用调制信号直接去控制载波的瞬时频率变化，间接调频是先将调制信号积分，然后对载波进行调相而实现调频[2-3]。

目前大部分高校开设的高频电路实验中都使用变容二极管直接调频电路来进行调频信号实验[4-5]。经典的高频电路教材中一般都会指出，直接调频电路的优点是电路结构简单，产生的调频信号频偏较大；缺点是中心频率不稳定，调频线性度相对较差，存在一定的调频失真[2-3]。

因此，变容二极管直接调频电路实验的目的主要是：①理解和掌握调频信号的基本特点，包括时域波形和频谱；②通过测量调频信号的中心频率（载波频率）、最大频偏、调频线性度等重要参数指标，掌握直接调频电路的工作原理、变容二极管最佳工作点选择方法，以及调制信号幅度对调频信号带宽和调频线性度的影响等[2-3]；③通过对实验数据的测量和分析讨论，掌握直接调频电路的优缺点[6]。

该实验传统的测量方法是使用示波器显示实验电路产生的调频信号时域波形，通过观察载波波形疏密程度的变化来定性判断调频波，但却无法定量测量调频波的中心频率和最大频偏[7-8]。条件较好的实验室可使用频谱仪观察实验电路产生的调频波频谱，根据教科书上调频信号带宽的定义[3]测量频带宽度和中心频率（载波频率）。但是该方法需要进行两次频谱测量，还需进行换算，存在固有测量误差，而对于调频线性度也只能基于频谱的对称性进行定性判断，无法简单直观地获得结果，本文后面还将对此详述。

本文对传统调频电路实验的测量内容进行了拓展深化，改进了测量手段，设计了一种高精度的调频信号参数测量方法，使学生在实验过程中能够定量地测量调频信号的主要参数指标，清晰直观地判断调频的线性度，从而大幅提升实验教学效果，很好地完成本实验的教学目标，并帮助学生深入理解直接调频电路的主要性能指标和优缺点。

2 实验电路制作

变容二极管直接调频电路的工作原理可参考高频电路教材[2-3]，此处不再赘述。

对于实验电路的制作，安排学生动手焊接制作实验使用的变容二极管直接调频电路，电路原理图如图1所示[9]。

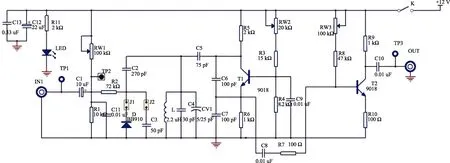
图1 变容二极管调频电路的原理图

晶体管T1 构成电容三端式振荡电路，其中电容C6、C7 构成正反馈回路，晶体管的基极通过耦合电容C9 在高频时交流接地，构成共基极组态的放大电路。

电阻RW2、R3、R4 是基极的直流偏置电阻，电阻R5 和R6 分别决定晶体管的集电极电压和发射极静态直流电流Ie。通常Ie 越大，晶体管放大电路的放大倍数也越大，振荡幅度越大，但同时谐波失真也会相应增大。Ie 过小时放大倍数不够，不满足A·F＞1 的起振条件（A 为晶体管电路的放大倍数，F 为反馈系数），电路无法起振。Ie 过大时晶体管有可能工作在饱和区，无法实现输入信号的正常放大，电路也不能振荡，因此一般选取Ie 在1～4 mA 之间。

电容的取值满足C6＞＞C5,C7＞＞C5，改变可变电容CV1 可调整振荡频率。电容C2 是一个小电容，当跳线J1 连接上后，变容二极管BB910 接入振荡电路中。滑动变阻器RW1 和电阻R1 构成分压电路，为变容二极管提供直流反偏电压即工作点。电阻R2 是一个大阻值的隔离电阻。调制信号从IN1 端输入，电容C1 是输入隔直电容。电容C11 是一个小电容，对高频振荡信号相当于短路，对低频调制信号相当于开路，从而保证低频调制信号可以加在变容二极管的两端，而振荡回路中的高频信号不会反射到低频调制信号输入端。

振荡信号从晶体管的发射极引出，后一级晶体管构成共射极电压放大，起隔离和缓冲作用。OUT 端是调频信号的输出端。示波器探头接在TP3 处测量振荡信号频率结果比较准确，如果直接在第一级的输出测量频率，示波器探头的输入电容会影响电路的振荡频率。

3 调频电路实验的传统测量方法

学生完成了调频电路的焊接制作后，设置变容二极管的直流反偏电压为6 V，输入正弦波调制信号频率为2.5 kHz、有效值为400 mV，将电路接50 Ω 负载时输出的调频信号接入示波器观察时域波形，如图2所示，图3 为调频信号对应的频谱。

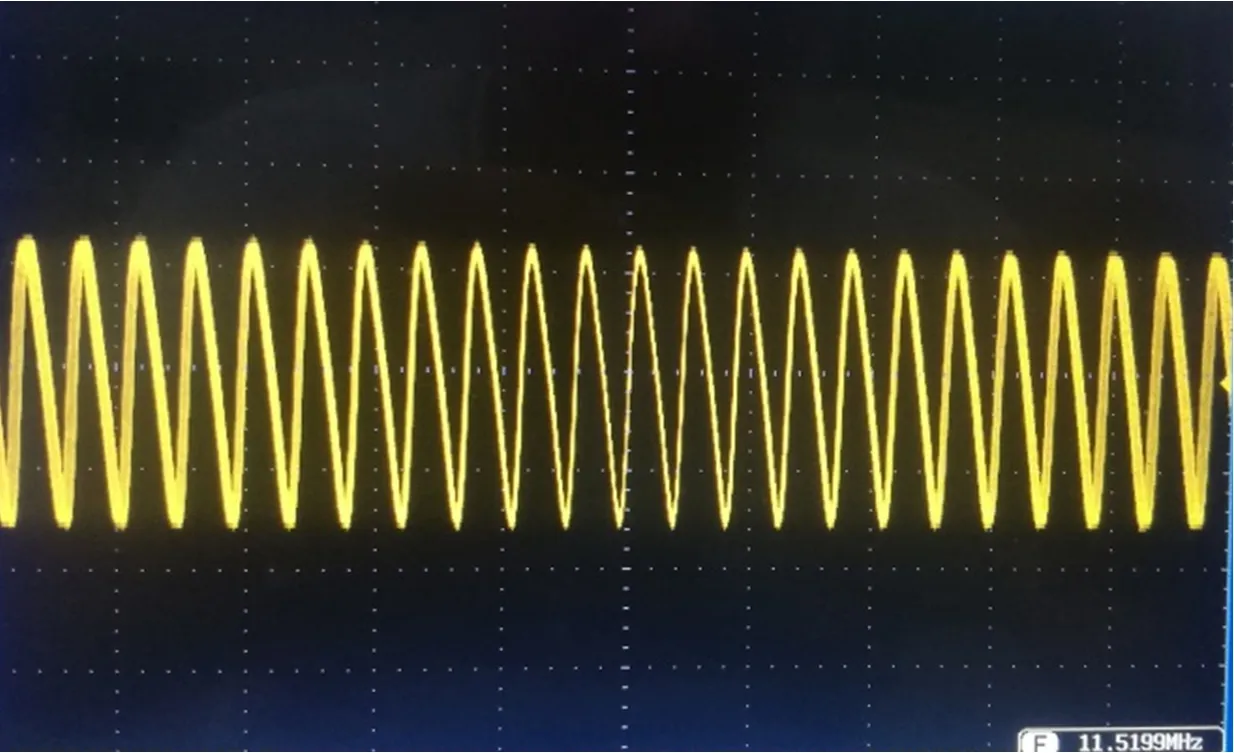
图2 调频信号的时域波形

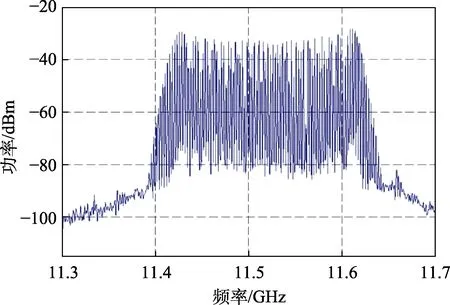
图3 调频信号的频谱

从时域波形上可以明显看出载波波形的疏密变化，证实电路产生了调频波，但却无法获知调频信号的中心频率、最大频偏，无法判断调频线性度。图3的调频信号频谱中包含很多根谱线，相邻两根频线的间隔都等于调制信号频率（2.5 kHz）。根据教科书上调频信号带宽的定义，忽略幅度小于未调制时载波幅度1%的谱线，计算保留下来的频谱分量宽度，作为调频信号带宽[2]。这样可测量出调频信号的最大频偏（近似地认为是频谱带宽的一半）约为111.3 kHz，中心频率（频谱分量的中心点）约为11.516 5 MHz。

但这一基于频谱仪的传统测量方法首先需测出未调制时的载波功率（无调制信号输入时，电路输出的振荡信号功率约为–14 dBm），再通过光标逐一测量各谱线的功率并进行换算，需要耗费较多时间，且存在一定的固有测量误差（频谱仪测量的调频波频带总是包含整数根谱线以及谱线的功率测量误差），测量精度不高。对于调频线性度的测量，则只能根据频谱分量在载波频率两侧的对称性进行定性判断，无法获得清晰直观的测量结果。

4 调频电路主要性能参数的高精度测量方法

所采用的测量方法为：使用实验室最普通的60～100 MHz 带宽的数字示波器，设置合适的存储深度（例如可选1 Mpts），调整水平时基，要求示波器面板屏幕上的波形数据采集的时间长度大于调制信号周期（此时实时采样率可能会下降，满足大于10 倍载波频率即可）。此时将示波器等效为一个8 位分辨率的高速ADC，用来采集调频信号的时域波形数据，然后将波形数据存储到U 盘中（有些示波器可直接通过USB接口和PC 机相连，使用提供的客户端软件），导入PC机的MATLAB 软件平台中[10]，使用希尔伯特瞬时频率算法[11-13]对采集的调频波时域波形数据进行计算，画出调频波瞬时频率的变化曲线，如图4 所示，图5是局部放大对比图。实验中示波器的数据存储深度设置为1 Mpts，记录调频信号波形数据的时间长度为2 ms，示波器的实时采样率为500 MSa/s。

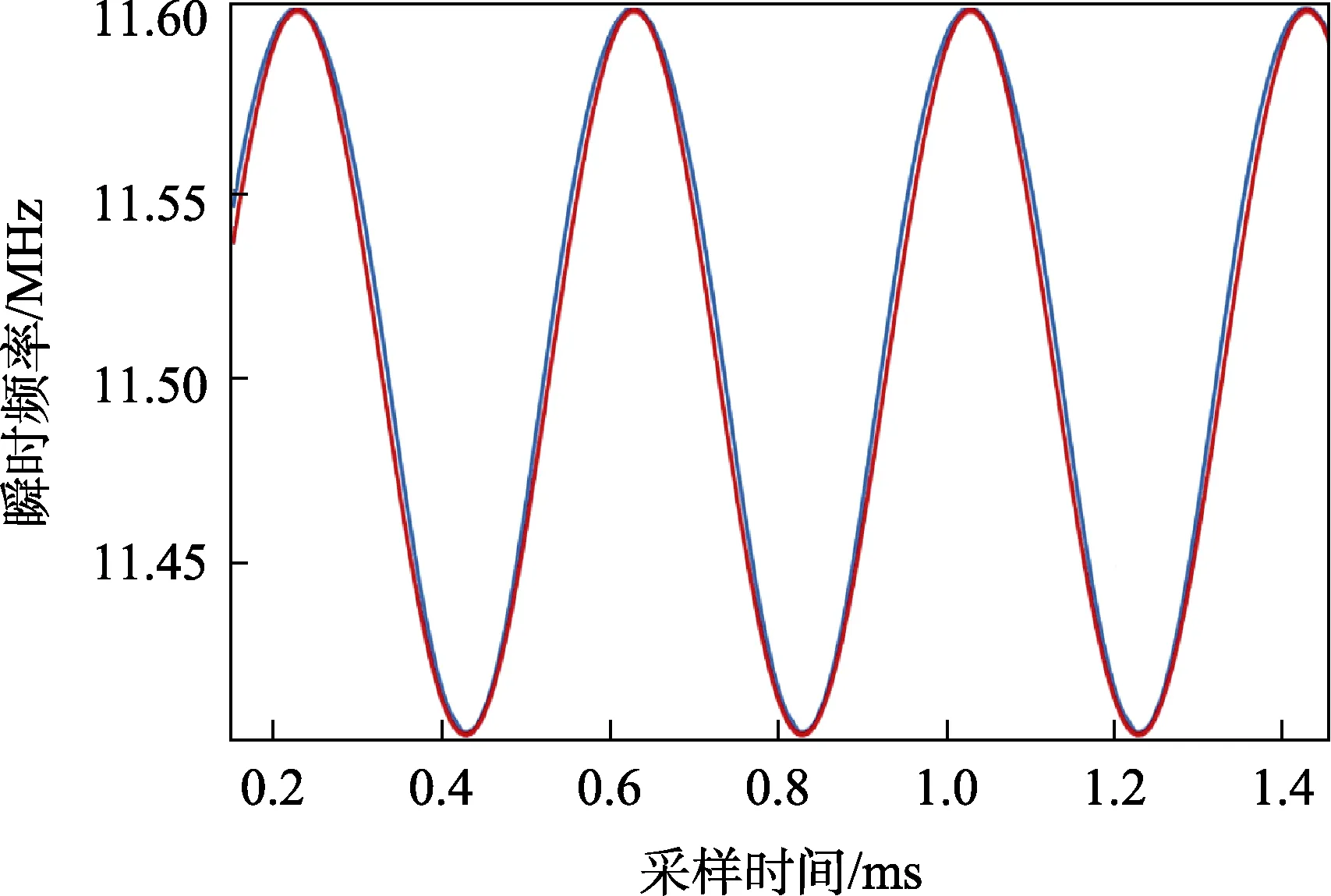
图4 调频信号的瞬时频率变化曲线图

图5 局部放大的瞬时频率变化曲线对比图

图中蓝色线是由电路产生的调频波计算出的瞬时频率变化曲线，红色线是中心频率和最大频偏相同时，理论上无失真调频波的瞬时频率变化曲线，二者画在一起用于对比调频线性失真度。从图4 和图5 的对比曲线图可以清楚地看到，调频过程中出现了非线性失真，实际频偏大于无失真的理论值。同时，从瞬时频率变化曲线中可直接读出最高频率fmax和最低频率fmin，很容易计算出此时调频波最大频偏为(fmaxfmin)/2，中心频率为(fmax+fmin)/2。

将调制信号的有效值降低为200 mV，其他条件不变，调频电路产生的调频波瞬时频率变化曲线如图6、图7 所示。此时电路的调频非线性失真明显减小，但实际频偏还是稍大于理论值。

图6 200 mV 时调频信号的瞬时频率变化曲线图

图7 200 mV 时局部放大的瞬时频率变化曲线对比图

接下来继续测量空载时电路产生的调频波性能指标参数，并整理测量数据如表1 所示，用传统频谱仪测量的数据如表2 所示。

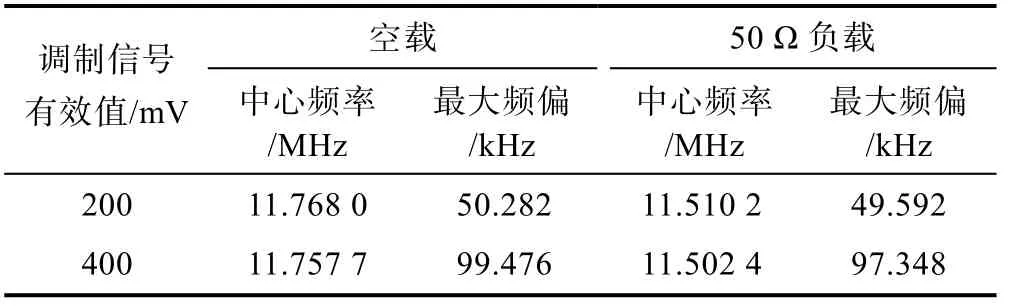
表1 用瞬时频率曲线测量的调频信号中心频率和最大频偏

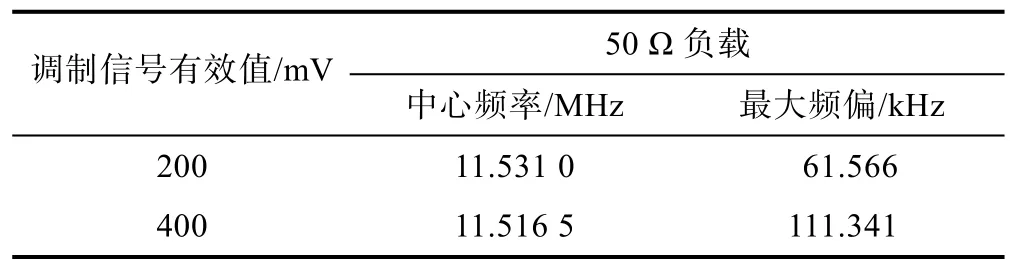
表2 用传统方法（频谱仪）测量的中心频率和最大频偏

从表1、表2 可以看出，频谱仪测量的中心频率和最大频偏数值都明显高于本文使用的瞬时频率测量法。主要原因为：①本文前面所分析的频谱仪的固有测量误差；②本调频实验电路的输出阻抗并不是50 Ω，没有与频谱仪的50 Ω 输入阻抗相匹配，也会引入一些振荡频率的测量误差。

需要特别说明的是，普通示波器使用的高速ADC采样精度只有8 bit，采样获得的时域波形数据会包含较大的量化噪声。另外，在MATLAB 中进行8 bit 位宽的波形数据运算时，会产生有限字长效应，直接对采样的波形数据使用希尔伯特变换计算瞬时频率[11-13]时会引起较大的计算误差。以调制信号有效值为400 mV、电路空载为例（其他条件不变），此时直接计算出的瞬时频率曲线如图8 所示，无法准确识别信号频率。

图8 直接计算的瞬时频率变化曲线图

考虑到量化噪声属于白噪声，在MATLAB 中对计算出的瞬时频率使用简单的均值滤波，可以大大改善量化噪声引入的计算误差；调频波的频率变化周期属于音频信号范围，可以对计算出的瞬时频率曲线用低通滤波器滤波进一步提高信噪比。最后，可得图9所示的清晰的瞬时频率变化曲线。

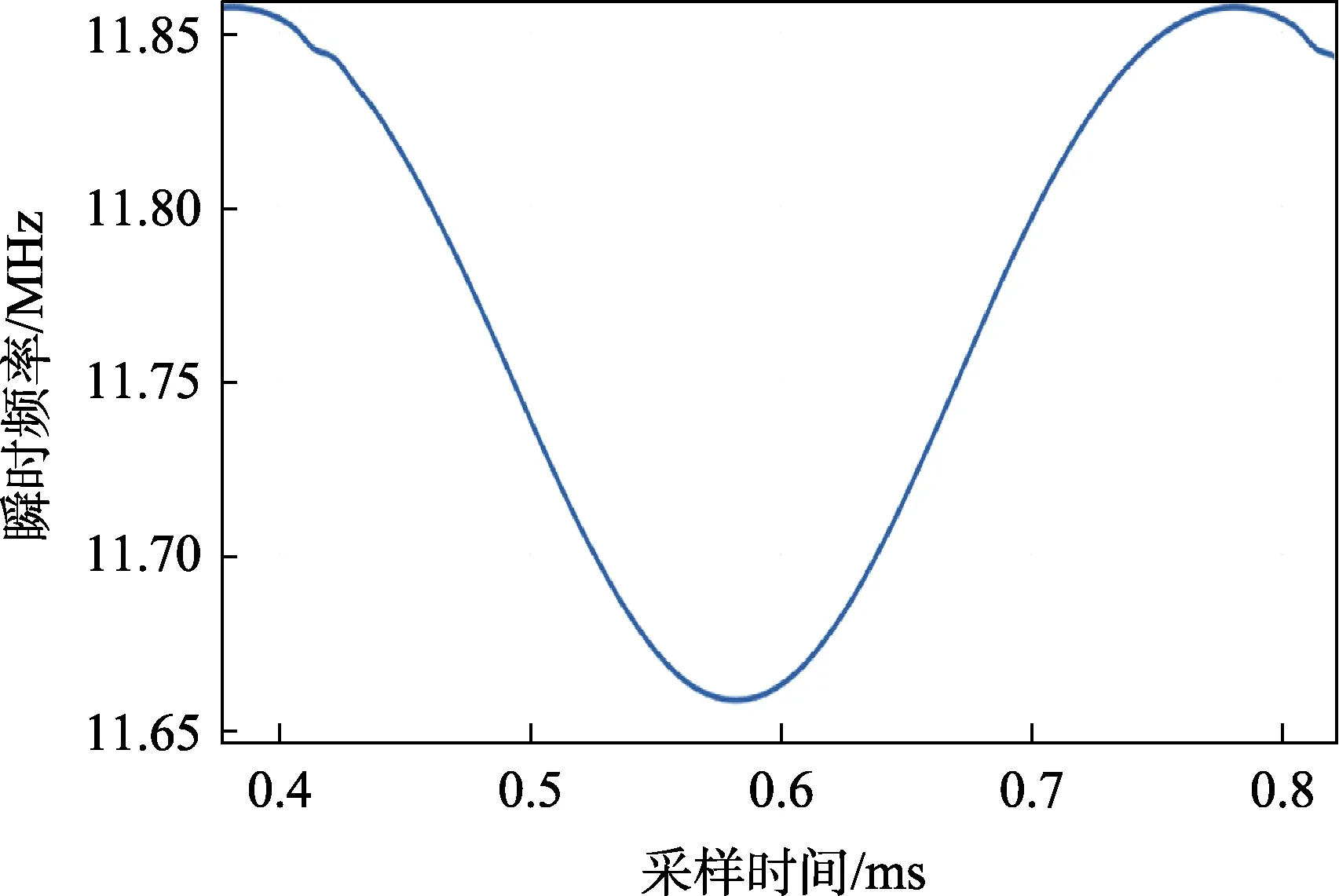
图9 滤波后的瞬时频率变化曲线图

5 进一步的实验测量和结果讨论

接下来通过以下实验来验证分析变容二极管在不同的直流反偏电压工作点条件下，实验电路产生的调频波主要参数指标和调制信号幅度的关系。

变容二极管的直流反偏电压分别设置为3 V、6 V、9 V，其中工作点在6 V，没有加入调制信号时，将振荡频率调整在11.7 MHz 附近，作为载波的中心频率。正弦波调制信号的频率为2.5 kHz，逐步增加调制信号的幅度，使用本文设计的测量方法计算并画出电路在不同条件下产生的调频波瞬时频率变化曲线，记录中心频率和最大频偏，如表3 所示。

表3 不同工作点下测量的中心频率和最大频偏

调制信号用三角波，幅度取1.13 V 和2.26 V，观察大信号调频时的线性失真度。测量的调频波瞬时频率曲线如图10—15 所示，蓝色线为实测的瞬时频率曲线，红色线为无失真调频波的瞬时频率曲线。

根据测量计算出的调频波瞬时频率特性曲线、中心频率和最大频偏数据，归纳出以下特点和规律。

（1）随着调制信号的加入，直接调频电路产生的调频波中心频率（载波频率）会产生一定的漂移；调制信号的幅度较大时（1.6 V 有效值）会引起中心频率较大的变化，证实了直接调频电路存在中心频率不稳定的缺点。

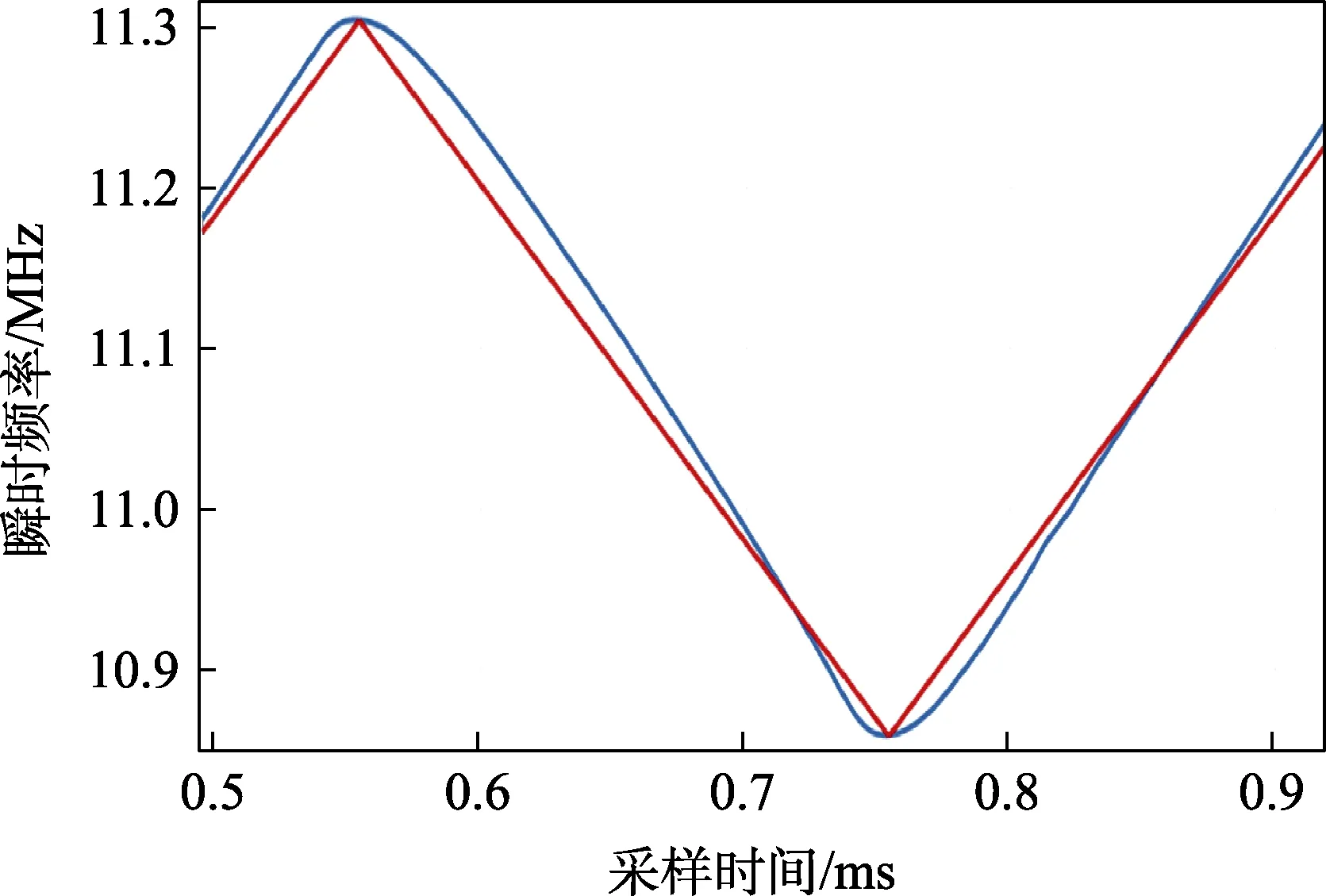
图10 3 V 工作点，调制信号幅度为1.12 V

图11 3 V 工作点，调制信号幅度为2.26 V

图12 6 V 工作点，调制信号幅度为1.12 V

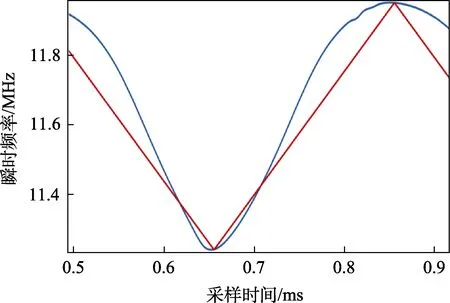
图13 6 V 工作点，调制信号幅度为2.26 V

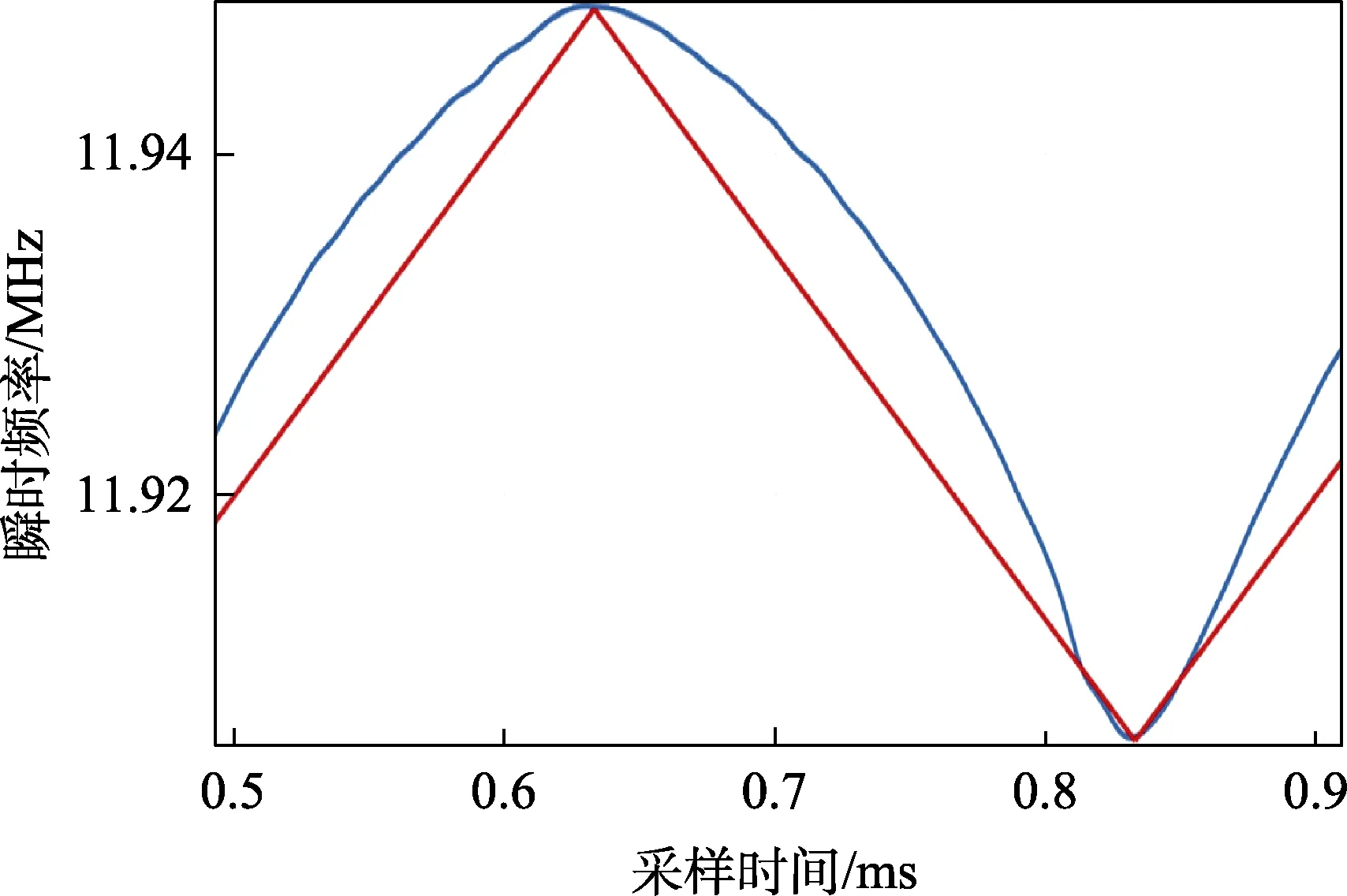
图14 9 V 工作点，调制信号幅度为1.12 V

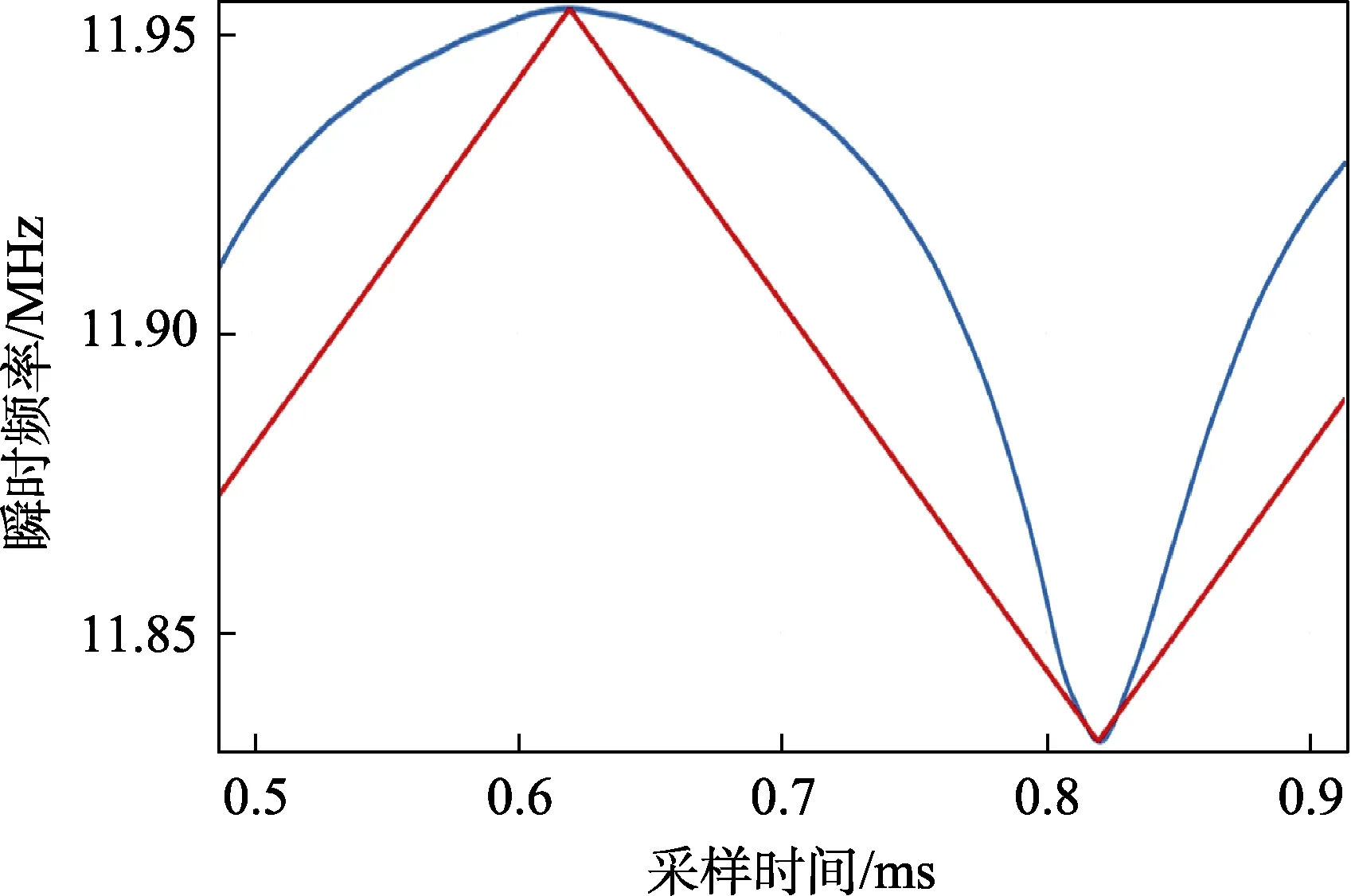
图15 9 V 工作点，调制信号幅度为2.26 V

（2）当调制信号幅度较小时，最大频偏和调制信号的幅度基本成正比，说明此时调频的线性度良好，调频非线性失真可以忽略；当调制信号的幅度较大时，正比关系不再满足，调频的线性度变差，此时出现了较大的调频非线性失真。

推荐理由:本书是三浦展继《第四消费时代》后又一力作，关注社会新生现象，并精准定义，赋予与时俱进的新名词，如熟年结婚、轻熟女、文化系腐女、墓友、共享街等。如作者所言，通过这些关键词，读者可以更全面和直接地解读这个时代。对于国内的读者来说，可以预见我们会否出现和日本类似的现象和文化。其实，国内已经陆续出现了与日本相似的风潮，如断舍离、共享生活、极简主义等，熟年结婚的人也是越来越多。那么，对于国内的商业来说，这些新群体就会产生新需求，必然也会带来商业的新机遇。

（3）当变容二极管的反偏工作点在3 V 和6 V时，调频灵敏度相对较高，产生的频偏也相应较大；反偏工作点在9 V 时，调频灵敏度下降，获得的频偏较小。

（4）反偏工作点在9 V 和3 V 时，大信号调频的线性失真度分别为最大和最小。

（5）为了兼顾电路产生的调频信号带宽和调频线性失真度，本实验电路的变容二极管最佳反偏工作点应选择在3 V 附近，同时需要控制调制信号的有效值在800 mV 以下。如果要求产生的调频波最大频偏不超过75 kHz，正弦调制信号的有效值应小于300 mV。

6 下变频实验的拓展

当调频波的最大频偏较小，而载波中心频率较高时，直接使用本实验设计的测量方法，有可能因为示波器实时采样率的下降（记录时间较长而存储深度一定时，实时采样率会下降），而使瞬时频率的测量精度下降。在实际应用中，可以使用混频器对待测调频波的载波频率进行下变频，从而降低对示波器实时采样频率的要求。

例如在本实验中，当变容二极管的直流反偏电压设置为9 V、调制信号的有效值为100 mV 时，产生的频偏较小（约为2.3 kHz），可使用二极管混频器模块，将载波中心频率降低到1 MHz 左右，此时测量的调频波性能参数见表3。直接测量和下变频后测量的瞬时频率变化曲线分别如图16、图17 所示。对比两图可知，下变频后瞬时频率曲线更加光滑，频率测量的精度提高了。原因是虽然示波器的实时采样频率不变，但每周期对调频波形的采样点数却是下变频前的11倍。经实验测试，在实时采样频率大于载波中心频率30 倍以上时，使用本文设计的测量方法可以获得较高的频率精度。

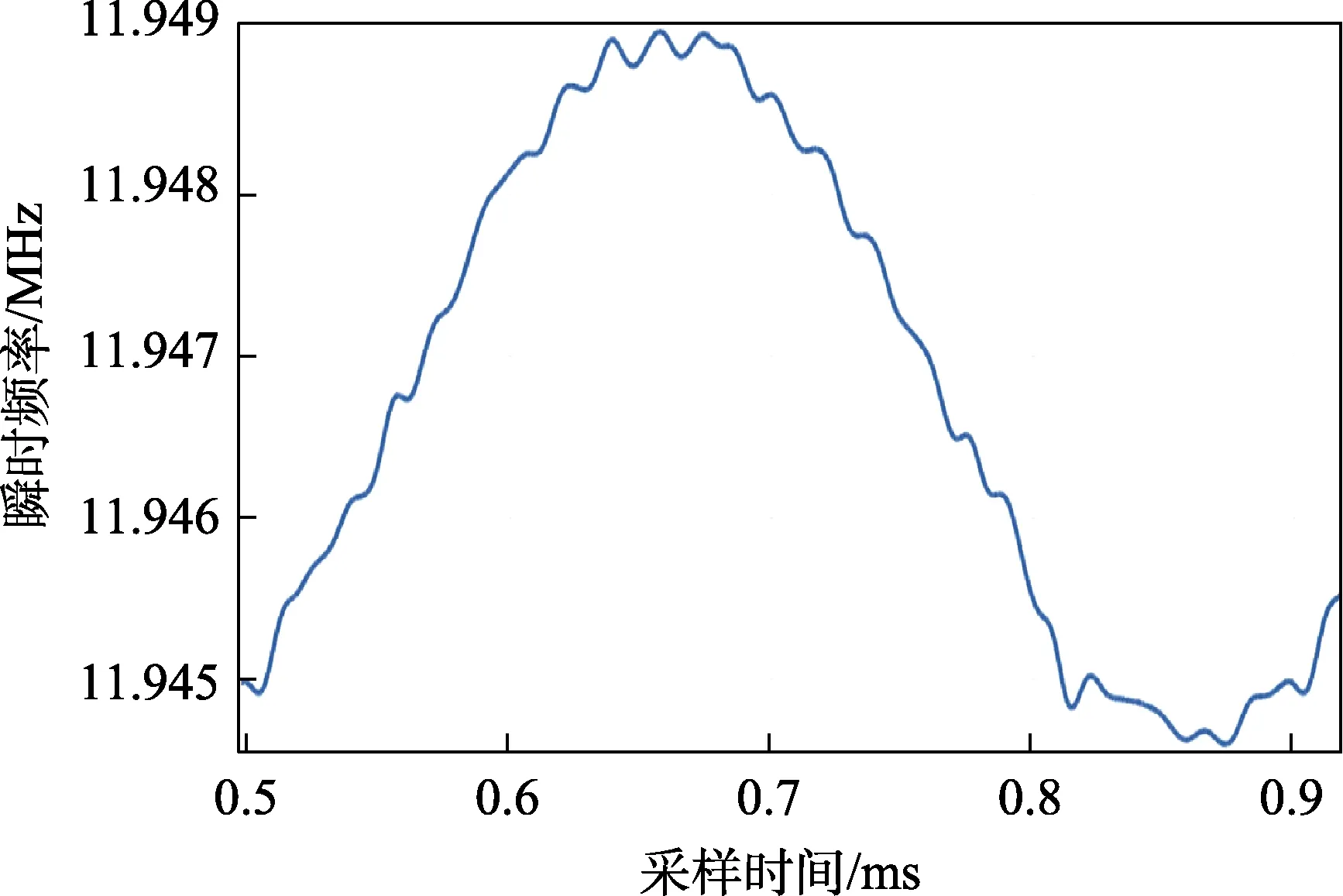
图16 直接测量的频率曲线

图17 下变频后测量的频率曲线

7 结语

在经典的变容二极管直接调频电路实验中使用本文设计的测量方法具有如下优点。

（1）无需使用价格相对较高的频谱仪，只使用实验室最常见的带波形数据存储功能的普通中低频数字示波器即可。

（2）能够较高精度地定量测量调频信号的主要性能参数，并清晰直观地判断调频线性度，使学生很好地掌握与实验相关的理论内容，较好地完成实验的所有教学目标。

（4）可以与下变频实验相结合，拓展实验内容，提高调频波最大频偏较小时的频率测量精度，同时降低对示波器实时采样率的要求。

（5）提高学生的实验兴趣，开拓思维，培养严谨的科学态度，提升实验技术素养。

本文设计的调频信号主要性能参数的定量测量方法，还可应用于相位编码信号解调、FSK 信号解调等场合；与鉴频电路或混频电路等实验内容相结合，可以设计成开放实验或综合性实验，适合在高校普通实验室进行推广应用。