地化分析数学方法的研究
唐莉
(大庆师范学院数学科学学院,黑龙江 大庆 163712)
1 气相色谱应用简介
气相色谱法是利用气体作流动相的色层分离分析方法。汽化的试样被载气(流动相)带入色谱柱中,柱中的固定相与试样中各组份分子作用力不同,各组份从色谱柱中流出时间不同,组份彼此分离。采用适当的鉴别和记录系统,制作标出各组份流出色谱柱的时间和浓度的色谱图。根据图中表明的出峰时间和顺序,可对化合物进行定性分析;根据峰的高低和面积大小,可对化合物进行定量分析。具有效能高、灵敏度高、选择性强、分析速度快、应用广泛、操作简便等特点。适用于易挥发有机化合物的定性、定量分析。对非挥发性的液体和固体物质,可通过高温裂解,气化后进行分析[7]。气相色谱分析常被用在地化分析技术当中,在漫长的地质历史过程中,水中的细菌就与部分烃类发生菌解和氧化作用,使正构烷烃减少,异构烃类与杂原子化合物增加,导致色谱峰较油层低,轻组分相对减少,主峰碳明显,碳数范围变窄等。经过对样品分析结合试油资料,就可以总结油层、油水同层、水层的典型谱图特征[10]。
在应用过程中总结了不同油质类型的谱图特征基本上响应值是以正态分布为主,峰形为三角形(包括前三角形、后三角形)、马鞍型等。用这些特征来判断油水层基本上是以图形来定义油水层特征,属于定性判断,且图形的微观变化无法表示出来,并且受人为因素影响太大,因此如何将图形数字化,用数字描述图形,建立气相色谱谱图解释模型;从气相色谱谱图解释模型入手,寻找敏感参数,建立定量解释标准是急需解决的难题[11]。
2 气相色谱数学表征技术研究
气相色谱分析技术可以检测储层中可流动部分的烃类,从气相色谱谱图解释模型入手,寻找敏感参数,为定量解释标准的建立奠定基础[9]。
气相色谱图目前可以由保留时间-响应值的坐标系、碳数-峰高坐标系、碳数-饱和烃面积坐标系及碳数-质量分数坐标系四种形式显示[12]。无论以哪一种形式显示的谱图,其大致形状是一致的。下面以碳数-质量分数坐标系的形式来对谱图的形态进行分析。从碳数-质量分数坐标系下的气相色谱图的形态可以联想到正态函数该函数取不同的σ值和不同的μ值时的图形如下。

图1 正态函数图像
为了很好地对气相色谱图进行表征,首先需要确定要表征的图形对象。原始谱图的横坐标是保留时间,纵坐标是响应值[8]。由于各种组分的保留时间不一致,因此本文将碳数作为横坐标,分别将峰高、峰面积、质量分数作为纵坐标,再对离散数据点进行拟合。当峰高、峰面积为纵坐标时,气相色谱拟合图数值差别较大,不容易进行对比,但取质量分数为纵坐标时的拟合却很好,一方面保留了图形的信息,另一方面不同井、层位和深度的差异相对很小,只是形状有些差异,比较便于进行表征。因此表征的对象定为将碳数作为横坐标、将质量分数作为纵坐标的气相色谱图[14]。
2.1 整体拟合原因分析
在后面的分析中会看到,气相色谱图表征的出发点是分段表征,因此要求在分段表征前先对所有离散数据点合理地分成几段[15]。离散点的分布从整体上看具有明显的变化趋势,但是离散点有时高、有时低,因此要对所有离散点进行整体拟合,以确定色谱图是单峰还是双峰。作整体拟合的另外一个原因是要用整体拟合函数的峰值点将所有离散数据点进行分段并参与分段后的拟合[16]。
2.2 函数拟合方法
函数拟合最常用的方法是最小二乘法,该法选取的基函数是{1,x,x2, …,xn},其最后一步要解一个线性代数方程组,而此方程组的系数矩阵是Hilbert矩阵,这就不易得到准确的拟合函数,出现这个问题的原因是基函数选择不恰当。所以,我们构造正交多项式族作为基函数,这时再求拟合函数的系数时,不用解方程组,不仅克服了系数矩阵病态的问题,同时也大大减少了计算量[17]。方法的原理如下:
假设给定m+1个数据点(xi,yi),i=0, 1, …,m其中x0<x1<…<xm。求n次(n<m)多项式使得在m+1个给定点上的偏差平方和最小。先约定关于点集{x0,x1, …,xm}的内积定义为
(1)正交函数族的构造
首先从线性无关的函数族{1,x,x2, …,xn}出发,利用施密特正交化方法构造出如下的函数族
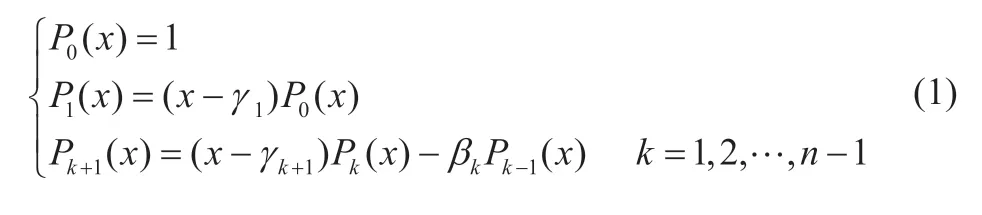
其中

下面证明这样构造的函数族确实是关于点集{x0,x1, …,xm}正交的。
由上述的表达式有
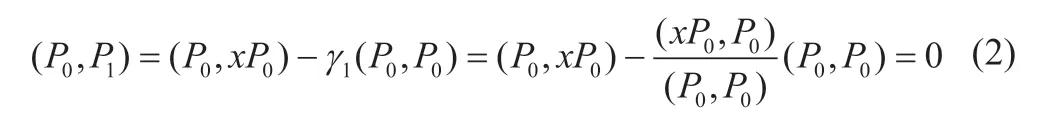
现假定(Pl,Ps)=0(l≠s)对s=0,1,…,l-1及l=0,1,…,k;k<n均成立。要证(Pk+1,Ps)=0,s=0,1,…,k,
由于(Pk+1,Ps)=((x-γk+1)Pk,Ps)-βk(Pk-1,Ps)=(xPk-Ps)-γk+1(Pk,Ps)-βk(Pk-1,Ps)
由归纳法假定,当0≤s≤k-2时(Pk,Ps)=0,(Pk-1,Ps)=0
另外,xPx(x)是首项系数为1的s+1次多项式,它可由P0,P1,…,Ps+1的线性组合表示,而s+1≤k-1,固由归纳法假定又有(xPx,Ps)≡(Pk,xPs)=0,所以当0≤s≤k-2时,(Pk+1,Ps)=0。
由(Pk+1,Pk-1)=(xPx,Pk-1)-γk+1(Pk,Pk-1)-βk(Pk-1,Pk-1)及假定有(Px,Pk-1)=0得

由上式和βk的表达式得(Pk+1,Pk-1)=(xPx,Pk-1)-βk(Pk-1,Pk-1)= (Pk,Pk)-(Pk,Pk)=0
最后

至此就证明了多项式{Pk(x)}(k=0,1,…,n,n<m)组成一个关于点集{xi}正交系[19]。
(2)拟合函数的求取
令S(x)=a0P0(x)+a1P1(x)+…+anPn(x)

由P0(x),P1(x),…,Pn(x)关于点集{x0,x1,…,xm}正交,即(Pi,Pj)=0,i≠j,方程组变为

所以方程组的解为

ak求出后,拟合函数就为S(x)=a0P0(x)+a1P1(x)+…+anPn(x)。
由于利用了正交多项式拟合,减少了工作量,也避免解方程组时出现的病态性。关于n的值不宜取得过大,否则会出现震荡现象,一般取n=5时拟合效果就很好了。由前面的分析看到图形的宽窄由于函数中标准差σ的改变而发生变化,最高点的纵坐标也发生了改变,这对图形表征不利[20]。因此我们选择概率函数 来取代正态函数,k值的大小可以反映概率函数图形的主要形态,参数个数变少了,还有明确的几何意义,这两类函数很适合作为表征函数[21]。
(1) 确定概率函数和二次函数的表征参数的数学方法研究
设此段离散数据点为(x0,y0), (x1,y1), (x2,y2),…,(xm,ym),其中整体拟合函数的顶点坐标为(x0,y0)[1]
两边取对数得:lny=lny0+k(x-x0)2
所以
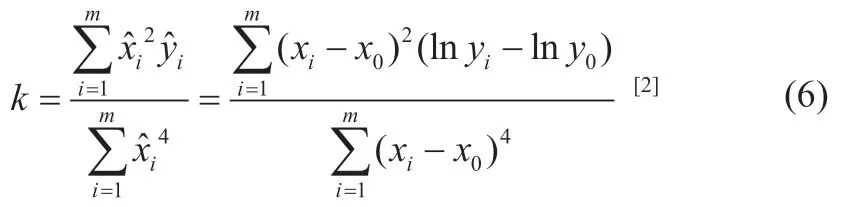
即

所以
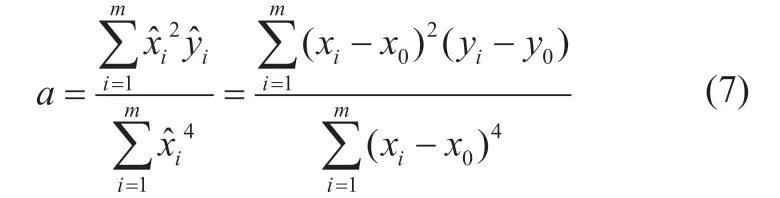
(2) 图形的分段表征函数的确定
由于已确定了所有的离散数据点的分段,并且研究了对每一段离散数据点用概率函数进行表征时表征参数k的求取公式和用二次函数进行表征时表征参数a的求取公式[3]。接下来就是对每段数据点进行表征拟合,通过比较来确定哪一类函数表征拟合的效果好就作为该离散数据段的表征函数。可以发现有单峰有双峰,经统一辨别,将所有谱图定义为四段,当拟合的曲线为单峰时,仅有第一段、第四段函数的参数信息;为双峰时,第一、二、三、四段函数的参数信息都存在[22]。
3 饱和烃气相色谱表征、参数求取及效果检验
下边首先对饱和烃气相色谱表征过程进行完整的说明,接着给出表征结果的效果检验,最后给出表征参数的统一定义[4]。 饱和烃气相色谱表征分以下四步进行:(1)选取数据库中要表征的气相色谱图;(2)拟合,确定峰形和顶点坐标;(3)利用拟合顶点将数据点进行分段;(4)对每一段确定表征函数及相应的参数值。为了说明图形表征及所求特征参数的有效性,需要定量分析利用特征参数恢复的图形和原始图形的近似程度[23]。
假设在原始离散点的坐标为(x0,y0), (x1,y1), (x2,y2),…,(xm,ym),每一段所选的特征函数及相应的特征参数其实就是得到了在区间[x0,xm]上的分段函数,求该分段函数在x0,x1, …,xm上的函数值,记为y0′,y0′,…,ym′。
(1) 图2是得到的表征函数及其参数进行图形恢复的效果图,图3是用拟合函数作为表征函数进行图形恢复的效果图[24]。
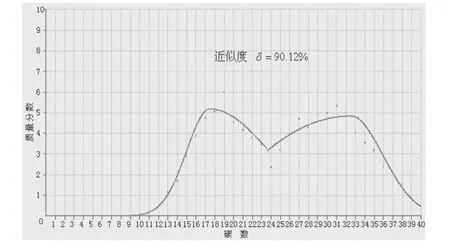
图2 图形恢复效果图

图3 图形恢复效果图
观察图形可知利用所研究的方法恢复效果的近似度大,且表征参数个数少,因此表征效果优于直接利用整体拟合函数作为表征函数进行表征的效果[6]。
(2) 图4是利用研究所得到的表征函数及其参数进行图形恢复的效果图,图5是用一个概率函数作为表征函数进行图形恢复的效果图[25]。
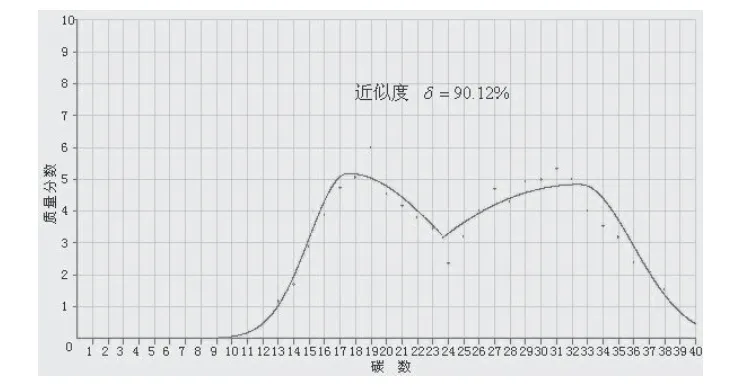
图4 图形恢复效果图
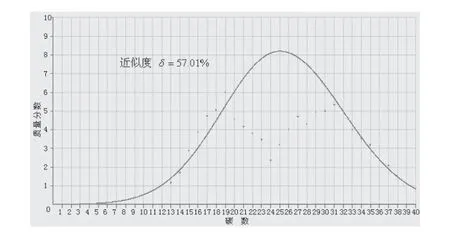
图5 图形恢复效果图
从恢复图形的效果及近似度可以看出,利用所研究的方法恢复效果优于后者。同时也说明了研究中所提出的分段表征的科学性和正确性[26]。
3.3 表征参数的规范定义及认识
观察气象色谱如图6、图7所示。

图6 单峰

图7 双峰
从选取的函数来看,是二次函数及概率函数,因此,将分段函数做如下定义:第一段二次函数的特征参数用a1表示,第一段概率函数的特征参数用k1表示;第二段二次函数的特征参数用a2表示,第二段概率函数的特征参数用k2表示;第三段二次函数的特征参数用a3表示,第三段概率函数的特征参数用k3表示;第四段二次函数的特征参数用a4表示,第四段概率函数的特征参数用k4表示。
4 结语
文章通过地化分析参数进行量化表征处理方法的研究,对气相色谱资料进行数学表征,求取有效的评价参数,所建立的地化分析单项资料的处理方法,有效地提高了算法的全面性,并通过对实例计算验证了算法的可行性及可用性,对地化分析参数进行量化表征处理方法的研究达到了预期的目的,为实际生产提供了很强的实际指导意义。本文的图形表征时主要考虑饱和烃面积的质量分数,这为下一步将未分辨面积作表征奠定了基础,接下来将进一步做探究。

