面向智能碾压机的位姿感知算法

谢 辉，刘煜光，闫 龙

(天津大学机械工程学院，天津 300072)

碾压机是筑路、筑坝中最重要的工程机械之一.碾压机的工作过程是按照施工要求对碾压条带进行往复碾压．为了保证碾压作业的高精准性和高覆盖率，车辆需要明确其确切的位置和方向．但是，土石料大坝堆石料区石块粒径可达60cm[1]，凹凸不平的地面不可避免地产生动作俯仰和横滚，使GPS天线端与车体中心不重合，测得的GPS数据存在误差和定位精度下降等问题．又由于复杂的山体阻碍卫星信号或环境中的障碍物形成多径干扰，导致接收GPS信号失真，出现短暂失效过程，而且碾压机的铰接式结构会导致前车身航向和后车身航向不一致，给航向感知带来困难．

利用多种传感器耦合技术可以获得精确的感知方案．为了克服GPS在障碍物阻挡信号处的定位精度，Suhr等[2]通过粒子滤波器将相机识别信息、数字地图与GPS信息进行融合，然而由于特征识别任务以及使用相机计算深度信息的困难，准确性受到限制．Gruyer等[3]与Schindler等[4]为了提高特征识别精度，利用相机检测车道标记，并与GPS和IMU融合来提高横向定位精度，然而在施工现场增加车道线会使施工工艺繁琐，而且车道线标记检测也会面临不同的光照和不良的车道标记等挑战．Wan等[5]利用LiDAR来改善定位系统准确性和鲁棒性，自适应地使用来自GNSS、LiDAR和IMU的信息构建多传感器融合框架，搭建了一套鲁棒的且精确度达到厘米级定位的系统，然而激光雷达在烟尘雨雪的环境下性能较差．

振动碾压机工作在复杂的路面环境下，给精确的定位和测向带来困难．Bian等[6]和Zhang等[7]为了消除由于路面地形波动带来的GPS定位位置和车体中心线的偏差，利用倾角传感器测量车辆实时倾斜角度，并通过传感器安装参数和几何关系对碾压机的位置偏差进行修正，但是在GPS出现短期失效时此种方法的作用大大减小．孟宇等[8]根据车辆当前行驶的位姿状态信息，利用航迹推算技术建立预见位姿状态模型，进行下一时刻采样点位置的位姿估计，但是位姿状态模型限制了算法的精度．黎永键等[9]采用三轴加速度计和三轴陀螺仪搭建姿态测量系统，实现动态环境下载体姿态估计，进而研究农业机械导航的姿态校正方法，但是在定位精度方面没有明显提高．谢辉等[10]为了改善智能振动碾压机在非结构化路面环境下的循迹效果，分析了外界扰动对车辆的航向角度及和位置的影响规律，并对航向角的影响构建实时扰动观测器进行估计，一定程度上提高了碾压机感知数据的精度，但是其本质上是控制算法对扰动的处理．

由上述研究结果可知，目前针对智能碾压机的铰接式结构及其复杂的工作环境，在位姿感知方面没有系统化的解决方法．为了进一步提高智能碾压机在复杂环境下定位和测向的精确性和普适性，本文基于以上研究内容提出面向智能碾压机的低成本位姿感知算法及感知方案，并在搭载传感器的碾压机上验证了算法的有效性．

1 感知平台描述

为应对智能碾压机在复杂环境下的感知需求，位姿感知平台主要搭载两类传感器：GPS和AHRS．两类传感器的安装方式如图1所示．GPS选用双置天线：前置天线是定位天线，安装在碾压机前车身横梁中心线，测量碾压机前车身位置信息；后置天线是定向天线，安装在碾压机后车身驾驶室中心线上，并与前后车身铰接中心在同一个竖直线上，测量碾压机前车身的航向信息．AHRS姿态传感器选用一套两个，前姿态传感器安装在前车身横梁中心线，耦合GPS输出精确位置信息；后姿态传感器安装在后车身中心线，通过数据驱动建模进行后车身航向角测量．

图1 感知平台示意Fig.1 Schematic diagram of perception platform

图2所示为本文提出的一种用于智能碾压机测量位置和航向信息的联合框架，通过有效地结合GPS、AHRS以及运动学模型，估算智能碾压机的最佳位置和前后车身航向．松耦合组合定位算法中使用陀螺仪和加速度计的数据积分作为误差状态卡尔曼滤波器的预测方程，其中包括加速计偏差和陀螺仪偏差；使用GPS数据对预测值进行校正，并加入一组运动约束关系，对预测值进行限定；EKF将估计的位置、速度和姿态等在内的校正结果反馈给预测方程和传感器偏差修正方程，以实现精确的定位．航向角估计算法中使用后姿态传感器输出的磁方位角进行数据分析，构建估计方程式；通过实验建模的方法对方程式中的常量进行标定；分析得出俯仰角和横滚角的变化致使方程式中出现变量，假设俯仰角和横滚角为输入，理想的变量为输出，利用BP神经网络进行在线学习，完整得出基于磁方位的航向角估计算法，有效地计算后车身的航向．

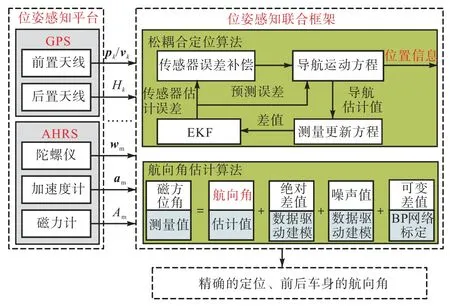
图2 感知算法框架示意Fig.2 Overview of the perception algorithm

2 松耦合定位算法

对于智能碾压机定位算法，选择当地导航坐标系(用n表示)和载体坐标系(用b表示)作为导航运动方程的参考基准．当地导航坐标系即地理坐标系是右手系，其按照坐标轴的指向和选取不同分为北东地坐标系(NED)和东北天坐标系(ENU)．本文取北东地坐标系(NED)为参考坐标系，选取5个主状态项构建系统状态变量，如表1所示．

表1 导航方程的主状态项Tab.1 Main state vector of navigation equation

2.1 面向定位的建模

2.1.1 构建传感器模型

AHRS姿态传感器中包括加速度计和陀螺仪．陀螺仪能够直接测量智能碾压机的角速度，并可以通过积分运算直接得到机体姿态角信息．陀螺仪测量中存在着温漂、零偏和随机漂移误差，其测量值mw可以简单概括为角速度值kw、陀螺仪偏差b,kw和测量随机噪声Nw的总和．其中陀螺仪偏差建模为随机游走过程．加速度计在静态或准静态下，可以提供重力加速度的固定垂直参考；在动态条件下，加速度的输出值与运动情况有关，包含重力加速度三轴分量和外部加速度．因此，同陀螺仪类似，其测量值ma可以描述为加速度值ka、重力引起的加速度量、加速度计偏差b,ka和测量随机噪声Na的总和．其中加速度计偏差建模为随机游走过程．由此得出如下方程[11]：

2.1.2 构建导航方程和误差方程

为描述智能碾压机前车身质心相对于北东地坐标系的位置变化，构建智能碾压机前车身质心平移运动的运动学方程，定义状态变量如表1所示．根据AHRS姿态传感器特性可知，加速度计输出的测量值经过坐标转换矩阵kR，得到北东地坐标系的值，然后积分得到相对于已知初始速度和位置的实时速度和位置．可得到位置kp和速度kv的运动学关系为

为描述智能碾压机前车身质心相对当地导航坐标系的空间姿态变化，构建碾压机前车身绕质心转动的运动学方程，定义状态变量如表1所示．利用姿态四元数和AHRS姿态传感器输出角速度表征相对当地导航坐标系的空间姿态变化，可得运动学方程为

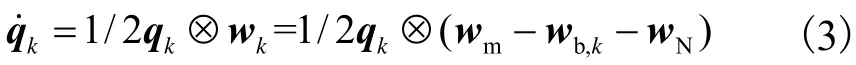
总结式(1)～(3)，根据表1状态变量，构建面向定位的运动学导航方程为

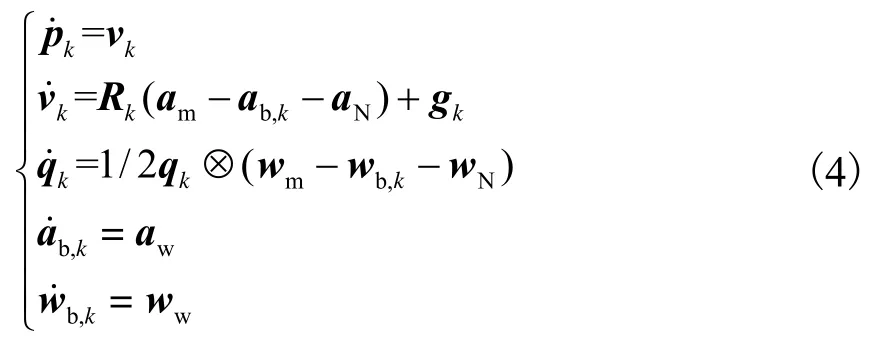
当使用基于误差状态的扩展卡尔曼滤波器(error-state extended Kalman filter，error-state EKF)时，利用传感器系统误差校准传感器输出信息，利用位置误差、速度误差和姿态误差对位置信息、速度信息和姿态信息进行校准，以此来提高定位准确性．定义误差状态

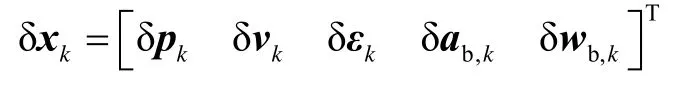
式中：δkp表示位置误差状态；δkv表示速度误差状态；δkε表示角度矢量误差状态；b,δka表示加速度偏差的误差状态；b,δkw表示角速度偏差的误差状态．基于导航运动方程，构建误差方程如下：

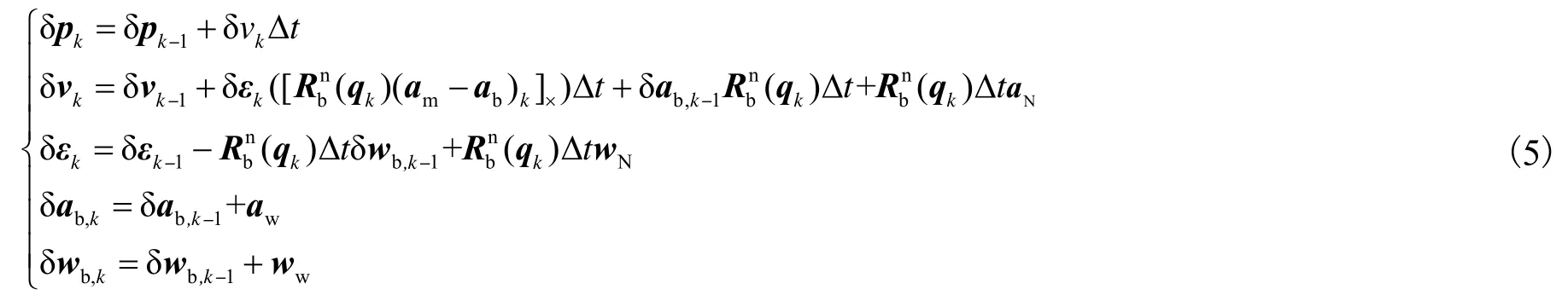
2.2 定位算法的设计

2.2.1 构建滤波器状态方程

根据非线性离散动态系统的状态空间方程一般表达形式，定义滤波器状态方程为

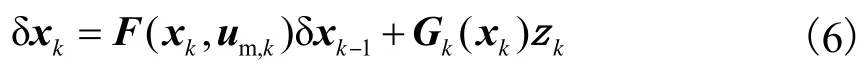
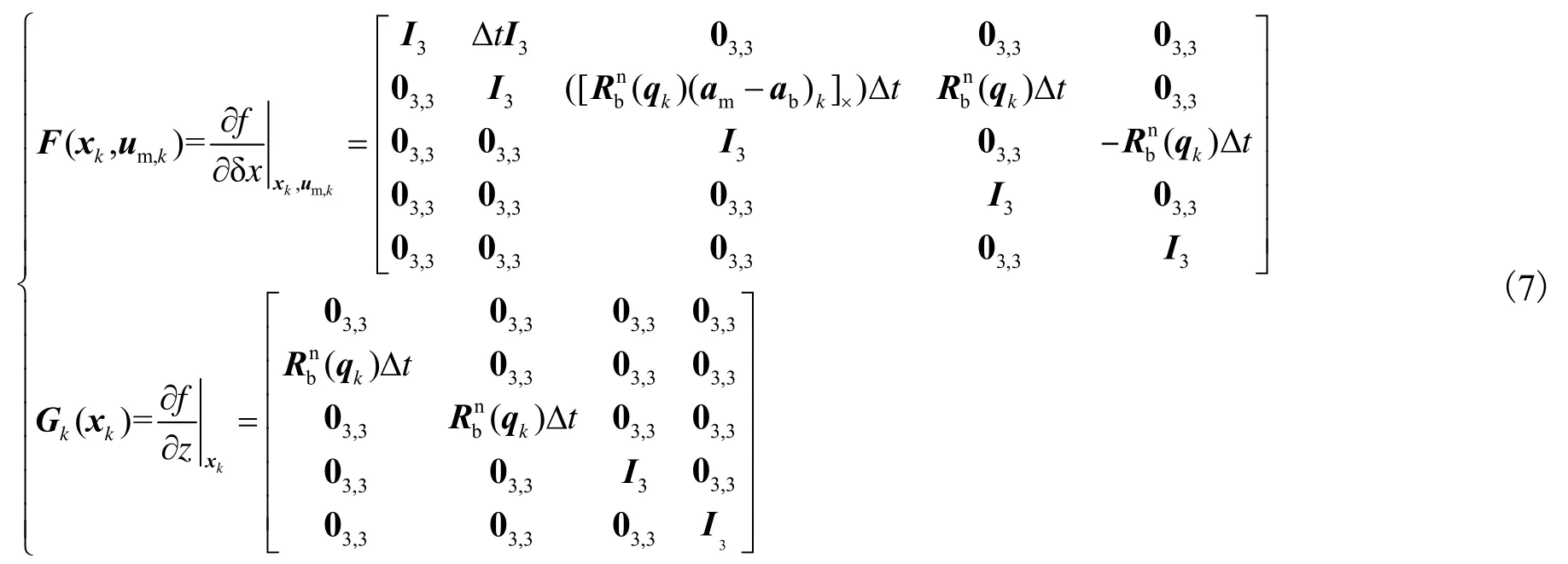
2.2.2 构建测量更新方程

误差状态扩展卡尔曼滤波测量更新过程是引入测量值来校正误差状态的后高斯估计．结合现有传感器和运动学常识，引入位置测量值和速度测量值来校正误差状态估计，并通过运动学约束来对预测过程进行限制．

1) GPS测量矩阵

假设GPS定位传感器测量值中包含高斯白噪声，构建GPS输出的位置、速度测量值和真值之间的关系式如下：

Error-state EKF测量矩阵是GPS测量值和导航运动方程的差值，可以表示为

2) 运动学约束

在构建的算法中，GPS测量值辅助AHRS进行状态偏差量的估计，进而减小融合值的误差，但是当GPS短暂失效时，基于AHRS的导航运动方程会迅速发散．在这里，考虑定义一组运动约束，用约束过滤法对导航运动过程实行限制．值；和分别表示GPS输出位置和速度．

在理想情况下，车体Y轴和Z轴的速度应该等于0，即

但在实际情况中，车体Y轴和Z轴的速度不可能是0，因此运动学约束条件必须放宽，基于此构建测量矩阵如下：

结合式(9)、(11)，滤波器测量矩阵为法有3个步骤．

(1) 基于导航运动方程的位置、速度、姿态和加速度偏差以及角速度偏差的递推运算，其中不考虑传感器的输入噪声．

(2) 基于误差状态方程和测量更新方程构建EKF的解算过程．误差方程负责及时向前推算当前状态变量和误差协方差估计的值，以便为下一个时间状态构造先验估计．测量更新方程负责校正误差状态的后高斯估计．

(3) 基于估计值进行真实状态的实时补偿．整个算法传播过程中不会传播整个误差状态，而是传播位置kp、速度kv、四元数kq、加速度偏差误差状态bδ,ka和角速度偏差误差状态 bδ,kw．在将估计的位置误差、速度误差和姿态四元数误差反馈到时间导航运动过程中用于校正后，这些误差状态被重置为0．

2.2.3 算法设计

Error-state EKF的基本流程如图3所示．核心算

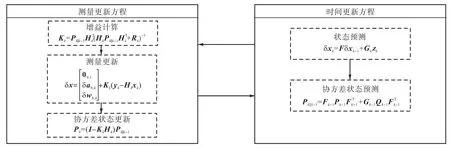
图3 误差状态扩展卡尔曼滤波的过程Fig.3 Process of error-state extended Kalman filter

3 航向角估计算法

本节使用的主要传感器是AHRS，利用AHRS输出的磁方位角和经验知识建立传感器输出值和真北方向航向角之间的关系方程，并通过大量的实验数据对方程中的分量进行标定，得出适应多种作业路况下的航向角估计式，完成基于数据驱动建模的航向角估计算法开发．

3.1 建立航向角估计的经验方程式

在一台装载AHRS和GPS的碾压机上，同时采集GPS输出航向角数据和AHRS输出方位角数据，执行结果如图4所示．

图4 方位角和航向角输出数据对比Fig.4 Comparison of azimuth and heading data

AHRS传感器中包含有三轴磁力计传感器，通过测量环境磁场强度输出所测载体方位角信息．由于地球的磁北极与地理北极不一致，因此在地球任意一点上的磁北方向与真北方向都不会完全重合，两者夹角称为磁偏角[12]．

假设GPS输出航向角准确，计算两者之间的差值，曲线效果如图5所示，从中可以很明显地看出方位角和航向角之间的差值不固定，在14°～27°之间波动．根据磁偏角原理，在同一个地区可以认为是定值，即 AHRS传感器输出的磁方位角和GPS输出航向角的夹角理想情况下可以认为是定值，因此分析图5中波动的差值可能是因为其他一些变量引起的．将图4趋势线中60～70s数据进行放大显示，部分曲线如图6所示．由图4、图6综合可知，方位角和航向角的变化趋势基本吻合．

图5 方位角和航向角差值Fig.5 Difference between azimuth and heading

图6 图4的局部放大图Fig.6 Local feature map of Fig.4

三轴磁力计的基本工作原理如下：通过测量三轴磁分量的数据以及此时载体所在位置的滚转角和俯仰角，计算磁力计在水平方向x轴和水平方向y轴的分量，而后通过三角函数计算方位角．从中可以得出，AHRS输出的磁方位角和俯仰角及滚转角有关系．在同一区域采集磁方位角数据，通过控制变量法分析可知，俯仰角和滚转角的变化的确会引起磁方位角的变化．

综上分析，建立磁力计测量模型经验方程式，第1部分为方位角和航向角差值部分，第2部分为姿态角引起的磁方位角变化，第3部分为航向角真值，第4部分为测量噪声．建立如下经验方程式：

式中： myaw表示AHRS输出的磁方位角； ryaw表示真实的航向角；θΔ 表示真北方向和输出的方位角的差值；βΔ 表示姿态角引起的磁方位角变化值；w表示测量噪声值．

3.2 经验方程式中常量的标定

根据构建的经验方程式可知，建立准确的航向角估计方程需要标定2个常量值，分别是理想情况下真北方向和传感器输出值的绝对差值、传感器输出值的噪声量．本节通过具体的实验对两值进行标定．

1) 噪声量标定

测量前将AHRS传感器置于水平的测量台上，确保周围无干扰，保证其输出值的准确性．连续采集10次测量数据，每次选取稳定后长度均为300s的测量信号，求得实测信号的均值．计算测量值与均值的差值和其方差分布，如图7和图8所示．从图中可以看出，其统计量的均值和方差分布比较稳定，且方差接近于0．所以从直观上分析，可以认为其噪声符合高斯分布，且其均值接近于0．

图7 噪声均值分布Fig.7 Distribution of noise mean

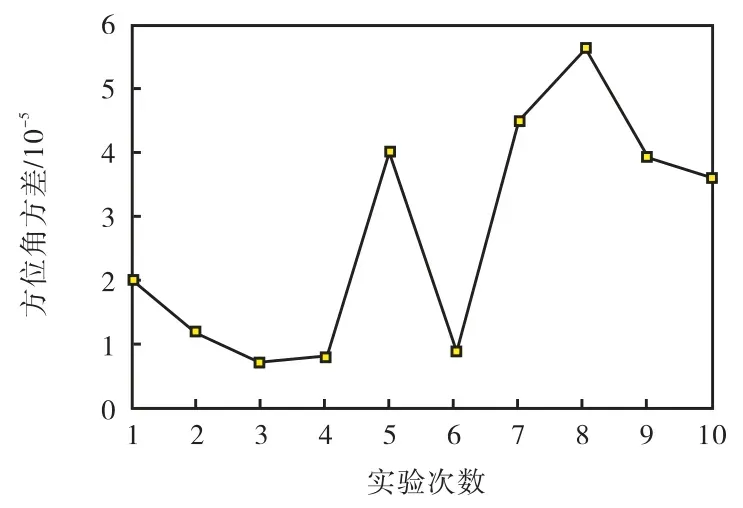
图8 噪声方差分布Fig.8 Distribution of noise mean variance

2) 绝对差值θΔ 标定

测量环境和前一组实验保持一样．将AHRS传感器和GPS依次置于水平的测量台上，从真北方向0°～360°，每30°左右进行1组实验，共进行12组实验．每组实验选取稳定后均为300s的测量数据，求得每组实验数据的均值．表2所示为依次对每一组数据的均值和真北方向值以及其差值的数据记录，其均值为21.62°，可作为理想情况下真北方向和传感器输出值的绝对差值．

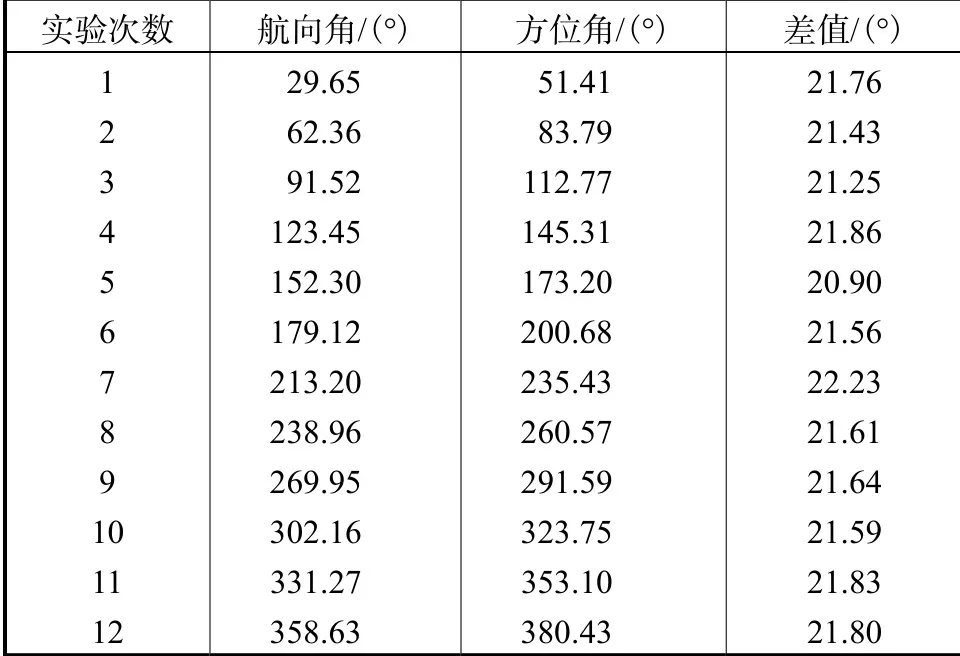
表2 实验数据记录Tab.2 Experimental data record

3.3 经验方程式中 βΔ的标定

采集大量的实验数据，其中包含有AHRS传感器方位角输出值、真北方向值、俯仰角和滚转角．对数据进行处理，记录俯仰角、滚转角和两角度引起的磁方位角变化值．利用具有突出自学习能力的反向传播神经网络对经验方程式中变量βΔ 进行标定．

反向传播(back propagation，BP)神经网络是一种数据信号的前向传播和反向传播两个过程组成的网络模型，主要原理是通过误差的反向传播来自动调整网络结构的参数．对于给定的输入，将产生最理想的输出[13]．本文设计的BP神经网络结构如图9所示．其中俯仰角和横滚角为输入，两角度引起的磁方位角变化值为输出，构建输入层、隐藏层和输出层3层神经网络结构．网络结构确定后最重要的步骤是确定其内部参数、训练函数、传递函数、学习过程中的学习率和允许的误差范围．根据经验值隐藏层的传递函数通常使用“tansig”或“logsig”．学习速率通常设置为0.01～0.70之间．如果学习速率太高，结果将变得不稳定，而如果学习速率太低，则网络收敛将变得缓慢．在本文中，将动量因子设为0.9，最大训练步数设置为10，允许误差为1×10-6．

图9 反向传播神经网络结构Fig.9 Architecture of BP neural network

BP神经网络的模型离线训练过程包括前向传播和反向传播．前向传播就是让信息从输入层进入网络，依次经过每一层的计算，得到最终输出结果的过程．反向传播是沿着反方向传递误差的过程．其基于梯度下降的策略，以目标的负梯度方向对参数进行近似调整，采用累计误差调整权值，使全局误差变小，最终达到神经网络中间权重和阈值的更新．

在线学习过程中，定义车辆实时的俯仰角和横滚角为输入，利用训练好的网络计算实时的βΔ 值．则航向角的估计方程式为

通过采集碾压机实时俯仰角和滚转角及AHRS输出磁方位角，带入式(14)中，计算航向角真值．

4 位姿感知算法实验验证

4.1 松耦合定位算法实验验证

为验证松耦合定位算法的有效性，在图1所示的无人驾驶碾压机平台上进行实验验证．无人驾驶碾压机工作在大约30m长的碾压条带上，分别记录其GPS输出信息和松耦合组合导航算法输出信息，并对其轨迹图进行分析，如图10所示．松耦合组合导航算法输出信息和GPS输出信息的均方根误差RMSE表征松耦合组合导航算法的精度，可得位置RMSE为10.76cm．可以看出，在正常行驶条件下，松耦合算法输出定位信息满足无人驾驶碾压机的工作需求．为了分析松耦合算法在复杂环境下的定位有效性，分别对GPS由于地形波动出现定位偏差量和GPS由于遮挡等出现短期失效进行有效性验证．

图10 松耦合算法的实验数据Fig.10 Experimental data of loose coupling algorithm

1) GPS定位位置出现偏差

无人驾驶碾压机作业环境地形凹凸不平，导致碾压机在实际运行过程中会发生较大角度的倾斜角，天线会随着车身晃动出现明显波动，导致实际输出位置产生偏差．设计实验工况，碾压机行驶过程中，前车身振动钢轮经过比较大的石头，车身有明显倾斜，GPS天线随着车身而倾斜，同时采集GPS输出位置轨迹和基于GPS/AHRS松耦合组合导航算法输出轨迹，进行对比实验，实验结果见图11．松耦合组合导航算法输出信息和GPS输出信息的均方根误差RMSE表征松耦合组合导航算法的精度，可得位置RMSE为6.81cm．

图11 松耦合算法与GPS对比Fig.11 Comparison chart of loose coupling algorithmand GPS

将图11中A处位置进行放大显示，如图12所示．从图中可以看出，松耦合组合导航输出的位置坐标很好地去除了原轨迹的波动，使得轨迹更为平滑．

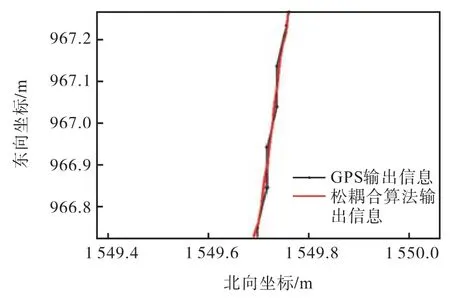
图12 A轨迹的局部放大Fig.12 Partial enlargement of trajectory A

将图11中B处位置进行放大显示，如图13所示．此时碾压机在东向位置969～970m位置处，滚转角为-2.1°，俯仰角为8.9°，根据几何修正式(15)得到GPS输出轨迹在北向位置偏差为6cm左右．而根据设计的松耦合组合导航算法的输出值和GPS原始输出信息之差也为6cm．证明松耦合组合导航算法可以较好地补偿由于地形波动导致的GPS定位位置偏差．

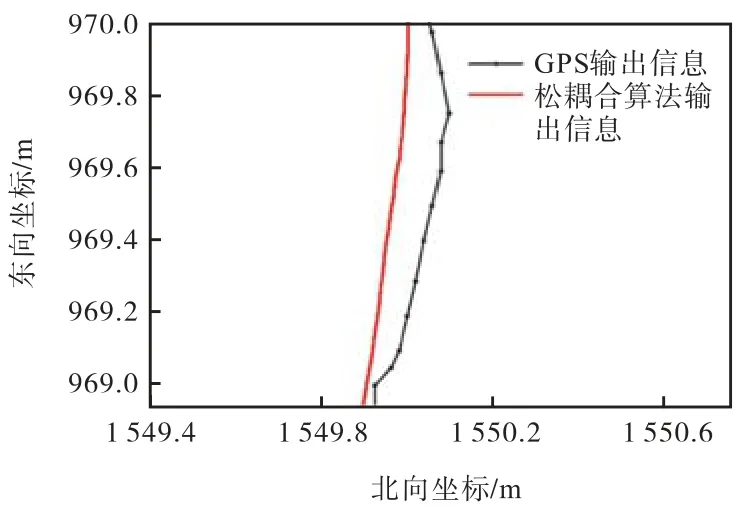
图13 B轨迹的局部放大图Fig.13 Partial enlargement of trajectory B

式中： eLon表示需要补偿的偏差量；hL表示GPS天线安装的高度；φ表示滚转角；θ表示俯仰角；ψ表示航向角．

2) GPS输出信号短时间失效

无人驾驶碾压机作业环境在两山之间，GPS在山体遮挡处可能会因为接收RTK基站信息不佳导致输出信息漂移过大；而且GPS接收卫星个数过少也会导致短时间内输出信息失真．针对GPS信号短时间失真问题，设计实验工况，采集一条GPS输出位置轨迹，将采集的GPS数据中间截去一段数据后作为松耦合组合导航算法的数据输入，模拟GPS短期失效问题进行对比实验分析．在组合导航算法中，首先根据接收卫星个数是否大于4颗和RTK基站接收是否正常来判断GPS输出是否满足要求；如果上述条件成立，则根据阈值范围判断数据输出是否准确．上述两组判断任有一组没有通过，则导航算法中认为GPS在k时刻输出观测值为k-1时刻的松耦合组合算法输出值．具体流程如图14所示．

图14 GPS短期失效处理流程Fig.14 Processing flow chart of GPS short-term failure

GPS输出数据完全正常时，松耦合定位算法输出轨迹与真实轨迹的偏差见图15(a)．在13.5s时间段，GPS输出数据分别失效1s、2s、3s、4s时间时，松耦合定位算法输出轨迹与真实的轨迹偏差分别如图15(b)～(e)所示．

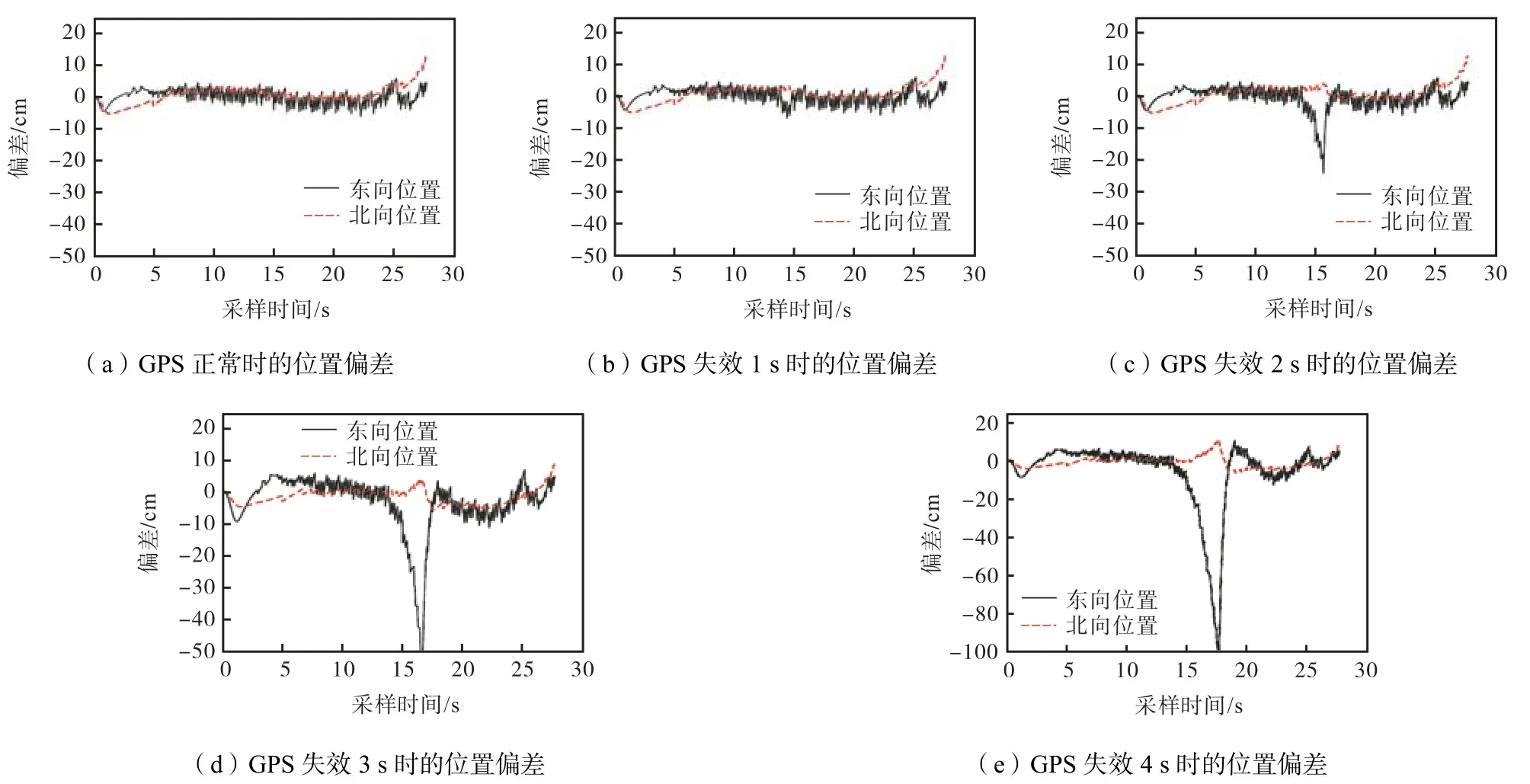
图15 轨迹偏差对比Fig.15 Comparison chart of trajectory deviation

GPS短期失效对于实验对象碾压机的东向位置坐标影响更大．因为error-state EKF在北向位置施加了运动约束，避免了系统的过快发散，证明了errorstate EKF算法中施加运动约束的正确性和必要性.失效2s时，东向位置瞬时偏差达到25cm，如图15(c)所示；失效3s时，东向位置瞬时偏差达到50cm，如图15(d)所示；失效4s时，位置瞬时偏差达到80cm，如图15(e)所示．但当在失效3s后GPS输出数据回复正常时，松耦合算法再次能起到精确的定位作用，如图16所示．

图16 GPS失效3s时的轨迹Fig.16 Trajectory during GPS failure for 3s

在GPS信号输出数据正常以及输出数据失效1s、2s、3s和4s情况下，统计误差RMSE值如表3所示．

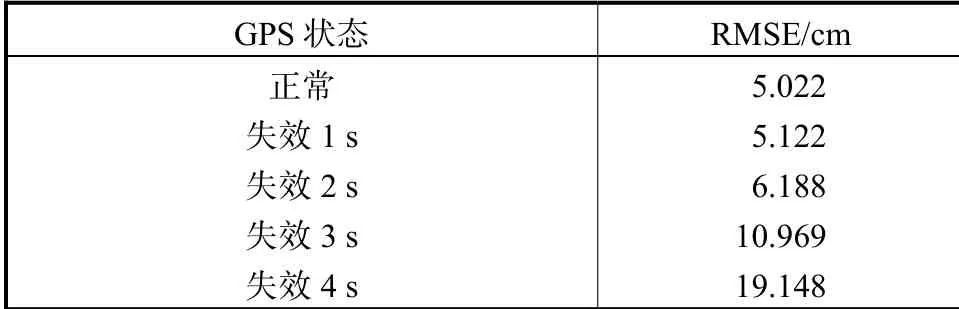
表3 不同情况下的RMSETab.3 RMSEs in different situations

综上分析，在GPS短时间失效3s之内，基于GPS/AHRS的松耦合组合导航算法输出位置信息可以较好地对系统进行补偿．失效3s时的误差值RMSE为10.969cm，起到精确的定位作用，验证了算法的可行性．

4.2 航向角估计算法实验验证

实验的测试平台如图1所示．为了验证航向角估计算法的可行性和准确性，在碾压机行驶工况下采集AHRS输出的磁方位角输出、俯仰角和滚转角，然后进行离线测试，并与GPS输出航向角进行对比分析．输出效果见图17．从图中可以看出，航向角估计值和GPS航向角输出值轨迹基本重合．经过计算，在当前数据中，航向角估计值和GPS输出航向角的最大误差为0.45°，如图18所示．

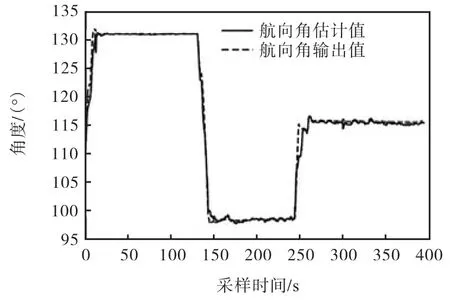
图17 低速下航向角估计值Fig.17 Verification of heading angle estimation in low dynamics

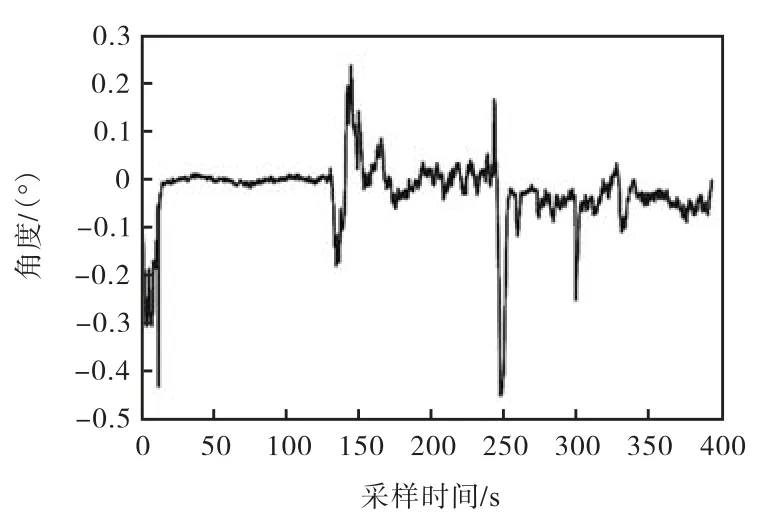
图18 估计值与GPS值的差值Fig.18 Difference between estimated value and GPS value

5 结 语

为了系统化地解决智能碾压机在复杂环境下的感知问题，提出了一种用于智能碾压机测量位置和航向信息的联合框架，有效地结合GPS、AHRS以及运动学模型，设计了基于GPS/AHRS的松耦合组合导航信息融合算法和基于数据驱动建模的航向角估计算法，估算智能碾压机的最佳位置和前后车身航向．实验证明，本文所提方法对于智能碾压机的定位和测向具有实用性．

智能碾压机在实际的运动中，GPS测量航向角受到碾压机横滚角和俯仰角的影响，而本文的航向角估计算法，在复杂的作业环境下也不能百分之百保证其准确性和鲁棒性．在未来的工作中，基于以上两种航向角数据，借鉴模型预测判断的机制对航向角进行优化，提升感知算法精度和性能．