基于变精度优粗集模型的一致性规则挖掘算法

陶 志，胡 柳，王 丹

（中国民航大学理学院，天津 300300）

粗糙集理论是由波兰数学家Pawlak[1]提出的一种处理不确定性数据知识的新理论，学界普遍称之为“数据驱动的数学”，自20 世纪80年代初提出以来，已获得越来越广泛的关注。基于粗糙集理论的数据挖掘方法目前已成为数据挖掘的主要方法之一，并被广泛应用于故障诊断、图像处理、声音识别、市场分析与预测等领域[2-6]。

粗糙集理论将知识理解为对已知数据集的分类能力，根据已知数据集自身的不可分辨关系，形成一对近似集合，对论域上的某个给定概念进行近似表达。该方法采用数据驱动的方式，本质上不需要任何辅助信息，仅依据数据本身提供的信息，就能够在保留关键信息的前提下对数据集合进行化简并求得知识的最小表达，从而建立决策规则，发现潜在和隐含的知识（规则），特别适合应用于知识发现与数据挖掘等领域[7]。在粗糙集数据分析中，属性之间的依赖关系通常表现为一组粗糙决策规则，而粗糙规则既有确定性（一致性）的，也有不确定性（不一致性）的。基于变精度优粗集模型的规则挖掘算法可在含有偏好信息的数据系统中进行数据挖掘，并通过预置近似精度因子，放宽标准优粗集的严格边界定义，从而克服了标准优势关系粗糙规则集对数据噪声过于敏感的缺点，具有一定的容错和抗噪声能力[8-9]。

1 基本概念

粗糙集理论核心是分类分析，根据已有给定问题的知识将问题论域进行划分，然后对划分后的每个组成部分确定其对某一概念的支持程度[10]。但在一些实际应用系统中，属性值域往往具有某种偏序关系，以此来表示优先等级，对于这类问题就不能再依据标准粗糙集中的等价关系来划分论域，而需要建立基于优势关系的粗糙集模型，以便针对相应问题进行分析和决策。

1.1 优势关系粗糙集

首先，引入优势关系粗糙集理论中的几个相关概念[11]。设形式化的偏好决策系统表示为

式中：U 为非空有限论域；AT=C∪D 为非空有限属性集，分为条件属性集C 和决策属性集D，C∩D=；V为属性值集，V=VC∪VD，VC为条件属性值集，VD为决策属性值集，且属性值具有偏好次序；f ∶U×AT→V 是一个信息函数（映射），表示对每个x∈U，q∈AT，有（fx，q）∈V。

在偏好决策系统中，依据决策属性集D 可将U 划分为有限个决策类集合：cl={clt，t∈T}，T={1，2，…，n}，通常认为决策属性划分的决策类集合是有序的，即∀r，s∈T，若r ＞s，则clr集合中对象从决策角度考虑优于cls的对象。

定义1设S=〈U，AT，V，f〉为偏好决策系统，C为条件属性集，若对于A⊆C 和∀q∈A，x，y∈U，总有q（x）≥q（y），则称x 在条件属性集A 上优于y，记为xDAy。

定义2设S=〈U，AT，V，f〉为偏好决策系统，C为条件属性集，对于给定的A⊆C 和∀x，y∈U，称集合DA+（x）={y∈U|yDAx}为属性集A 关于对象x 的优势集，称集合DA-（x）={y∈U|xDAy}为属性集A 关于对象x 的劣势集。

定义3在偏好决策系统S=〈U，AT，V，f〉中，clt为决策属性集D 下的一个决策类，clt的向上累积集（简称clt的优势类）为的向下累积集（简称clt的劣势类）为

关于优势关系粗糙集模型的下近似和上近似定义如下。

定义4设S=〈U，AT，V，f〉为偏好决策系统，属性集A⊆C，则向上累积集clt≥关于属性集A 的下、上近似集及其边界域分别为

向下累积集clt≤关于属性集A 的下、上近似集及其边界域分别为

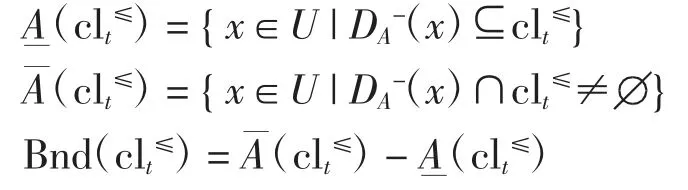
1.2 变精度优粗集

优势关系粗糙集严格按照优势集合DA+（x）（或劣势集DA-（x））来进行分类，存在由其“刚性”特质所决定的局限性，如对扰动（噪声）数据过于敏感。本节所提出的变精度优粗集模型具有某种“柔性”特征，克服了优粗集模型对数据噪声过于敏感的缺点，适用范围更加广泛。

下面是变精度优粗集的下近似和上近似的定义。

定义5设S=〈U，AT，V，f〉是一个偏好决策系统，属性集A⊆C，clt≥是clt的一个优势类，则向上累积集clt≥依参数α 的下、上近似集定义为

式中：|·|表示集合的势；参数α 取0.5 ＜α≤1，可看出，当α=1时，变精度优粗集即变为优势关系粗糙集。相应地，集合clt≥依参数α 的粗糙近似边界为

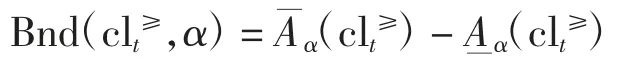
对向下累积集clt≤依参数α 的下、上近似集及其边界域分别定义为

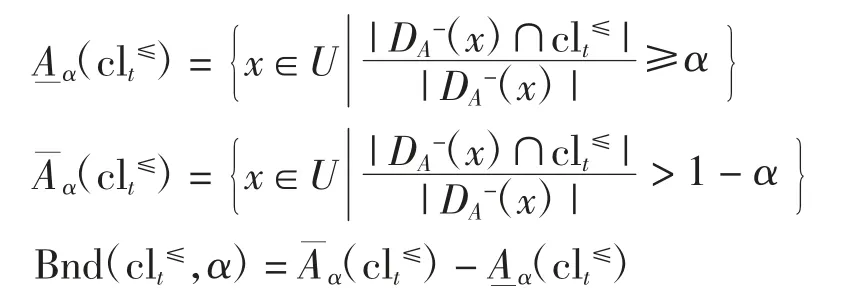
2 基于变精度优粗集模型的粗糙规则集

2.1 粗糙规则集

在变精度优粗集模型中，通过对优势类的粗糙近似可形成一组粗糙决策规则，从数据中发现这些规则是粗糙集数据分析的主要目标。

假设0.5 ＜α≤1，A⊆C，某优势类clt≥的下近似集为，则与下近似集对应的是“至少”一致性决策规则，即对每个对象均对应如下一条“至少”一致性决策规则x∈DA+（x）→x∈clt≥，简记为DA+（x）→clt≥。同样，与下近似集对应的是“至多”一致性决策规则，简记为DA-（x）→clt≤。以上规则：当α=1 时，为完全一致性规则，即在优势关系意义下的一致性规则；否则，称为“几乎一致性”规则，即准确度不低于阈值α 且小于1 的规则。将“几乎一致性”规则在阈值α 水平上与完全一致性规则等同看待，可有效处理噪声对数据一致性的影响。将“完全一致性”规则与“几乎一致性”规则统称为α 一致性规则，而将准确度低于阈值α 的规则称作不一致性规则。

定义6设Mi={cl1≥，cl2≥，…，clt≥}，1≤t≤n，则称如下决策规则为依参数α 的“至少”不一致规则。

2.2 规则评价

对于一个决策规则DA+（x）→clt≥，一般可用准确度和覆盖度来评价其优劣。

定义7规则DA+（x）→clt≥的准确度为

定义8规则DA+（x）→clt≥的覆盖度为

准确度反映规则的准确程度，覆盖度在一定程度上表达了规则随机性大小，期望得到既有高准确度又有高覆盖度的规则，即得到的规则要在不一致性和随机性两方面均得到一定程度的消除。

2.3 不确定性量度

粗糙规则集的不确定性主要有两个原因[12-13]：一个来自于边界域，另一个体现在论域中对象的不可分辨性，这两种不确定性反映了不确定性的不同方面，不能互相代替[14-15]。

以下修正知识粒度的概念可用于从不确定性的两个方面精确地测量粗糙规则集的不确定性。

定义9设S=〈U，AT，V，f〉是一个偏好决策系统，0.5 ＜α≤1，D 将U 划分为有限个决策类，cl={cl1，cl2，…，cln}，则∀A⊆C，修正知识粒度为

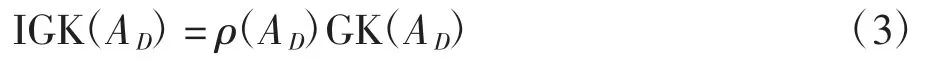
式中：ρ（AD）表示由边界域引起的不确定性，即

GK（AD）表示由分类不精细引起的不确定性，即

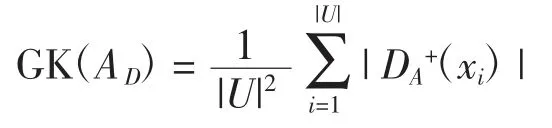
修正知识粒度满足以下性质。

性质10≤IGK（AD）≤1。

性质2设S=〈U，AT，V，f〉是一个偏好决策系统，若A′⊆A，则有IGK（AD）≤IGK（AD′）。

证明由于A′⊆A，则对∀x∈U，必满足DA+（x）⊆DA′+（x），从而有|DA+（xi）|≤|DA′+（xi）|，所以GK（AD）≤GK（AD′）。

另一方面，由于A′⊆A，则对∀x∈U，必满足DA+（x）⊆DA′+（x），则有，因此，有|BndA（clt≥，α）|≤|BndA′（clt≥，α）|。

同理，可证|BndA（clt≤，α）|≤|BndA′（clt≤，α）|，从而有ρ（AD）≤ρ（AD′）。

综上，则有ρ（AD）GK（AD）≤ρ（AD′）GK（AD′），即IGK（AD）≤IGK（AD′）。

证毕。

性质2 说明，修正知识粒度对属性集合具有单调性，当属性增加、分类能力增强时，修正知识粒度会随之减小，反之，则会增大。该性质为后续启发式属性约简算法提供了理论基础。

3 基于修正知识粒度的属性相对约简方法

一般来说，根据对决策结果影响程度的不同，属性的重要性程度也不同。按照属性对决策结果的影响，属性可分为核心属性、相对必要属性和不必要属性3 类，去除不必要属性是属性约简问题的核心。因此，首先引入条件属性对决策重要性的定义如下。

定义10设S=〈U，AT，V，f〉是一个偏好决策系统，∀B⊆C，若a∈B，则a 对属性集B 的重要性定义为

SigB（a）=IGK（（B-{a}）D）-IGK（BD）。

上述定义表明属性a∈B 对B 的重要性可由B 中去掉a 后所引起的修正知识粒度变化的大小来度量。

由以上定义可推出如下性质。

性质30≤SigB（a）≤1。

性质4属性a 在属性集B 中是必要的当且仅当SigB（a）＞0。

性质5核心属性集Core（B）={a∈B|SigB（a）＞0}。

性质4 表明：当SigB（a）＞0 时，说明a 是B 中必要的；当SigB（a）=0 时，说明a 是B 中不必要的。性质5给出求取核心属性集的方法，核心属性集是求取所有属性约简的起点。

定义11设S=〈U，AT，V，f〉是一个偏好决策系统，∀B⊆C，若B 是一个相对属性约简，当且仅当B 满足：①IGK（BD）=IGK（CD）；②∀a∈B⇒SigB（a）＞0。

定义11 从修正知识粒度的角度提供了属性相对约简的定义，为后面求取属性相对约简算法奠定了理论基础。

4 阈值α 对粗糙规则集影响分析

对于变精度粗糙规则集而言，如果条件属性子集和决策属性均已确定，则阈值α 取值不同就会得到不同的粗糙规则集，研究α 的变化对规则集的影响很重要，其意义是帮助决策者找出实际问题中的关键环节，从而起到辅助决策的作用。

4.1 相对粗糙规则集与绝对粗糙规则集

某一优势类clt≥的边界域可表示为Bnd（clt≥，α）=如果或，此时，称集合clt≥为α 可辨别的，否则称clt≥为α 不可辨别的。

集合的可辨别性依赖于α 的取值，易证明下列定理。

定理1若clt≥在阈值0.5 ＜α≤1 水平上是可辨别的，则clt≥在任何α1＜α 水平上也是可辨别的。

对于粗糙规则集，A→αD 若存在充分小的阈值α使得W=U，即在优势关系粗糙集意义下，所有不一致性规则在α 水平上均可变成一致性规则，此时称此粗糙规则集为相对粗糙规则集。相对粗糙规则集在某一α 水平上不再包含不一致性规则，完全由α 一致性规则组成，此时亦称其达到弱完全一致。反过来，无论α取值多小，粗糙规则集中均含有不一致性规则，此时，称此粗糙规则集为绝对粗糙规则集。

定理2设S=〈U，AT，V，f〉是一个偏好决策系统，D 将U 划分为有限个决策类，cl={cl1，cl2，…，cln}，则粗糙规则集是相对粗糙规则集的充要条件是：

4.2 阈值α 灵敏度分析

设A 是条件属性子集，D 是决策属性集，D 将U划分为有限个决策类，cl={cl1，cl2，…，cln}，对确定的A、D 和α 可产生确定的粗糙规则集A→αD。灵敏度分析是指在A、D 已确定的情况下，参数α 在何种范围内变化时，不会对已生成的规则集产生影响，参数α 的这一变化范围即α 的阈值平稳区间。

对每个决策类clt（1≤t≤n），clt≥为向上累积集，令

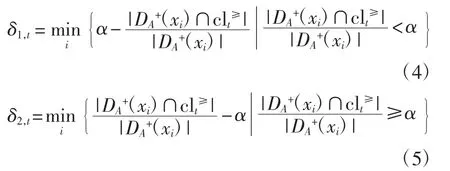
同理，对于向下累积集clt≤，令

5 一致性规则挖掘算法

变精度优粗集模型中一致性规则集的形成可由以下3 个算法来实现。

5.1 求取相对属性约简算法

输入偏好决策系统S=〈U，AT，V，f〉；阈值0.5 ＜α≤1。

输出属性相对约简集C*⊆C。

步骤1由式（3）计算系统的修正知识粒度。

步骤2赋值计算出Core（C）={a∈C|SigC（a）＞0}。若IGK（Core（C）D）=IGK（CD），则C*=Core（C），输出C*，终止计算（此时Core（C）为最小相对约简）；否则C*=Core（C），继续执行步骤3。

步骤3

1）对∀a∈C-C*，计算出SigC*∪{a}（a）；

3）若IGK（C*D）= IGK（CD），则输出C*终止计算（此时C*即为一个相对约简）；否则转步骤1）。

5.2 一致性规则提取算法

输入一个得到化简的偏好决策系统S*=〈U，C*∪D，V，f〉；阈值0.5 ＜α≤1。

输出α 一致性规则集

步骤1输入一条新对象的条件属性值C1。

步骤2对于决策表S*：

1）计算属性值优于C1中属性值的元素个数N；

2）对每个不同的决策属性值dj（j=1，2，…，n），求出条件属性值优于C1而决策属性值满足dj≥j 的元素个数Mj，并求出αj=Mj/N；

3）判断是否存在αj≥α，如果是，则取j = min{ j |αj≥α}，转步骤4）；否则，转步骤3；

5）判断αj是否为1，如果是，则输出“完全一致性规则”至规则表，同时令μ=1 并由式（2）计算出该条规则的覆盖度λ 并转步骤3；否则，输出“几乎一致性规则”至规则表，同时由式（1）、式（2）计算出该条规则的准确度μ（此时μ≥α）和覆盖度λ 并转步骤3。

步骤3判断是否输完所有对象条件属性值，如果不是，则转步骤1；否则，终止计算。

5.3 阈值α 影响性分析算法

输入偏好决策系统S*=〈U，C*∪D，V，f〉，α 一致性规则集，阈值0.5 ＜α≤1。

输出输出是相对（或绝对）粗糙规则集及参数α 的阈值平稳区间。

步骤1将S*划分为有限个决策类，cl={cl1，cl2，…，cln}。

步骤2判定是否对每个优势类clt≥（t=1，2，…，n）都有且对每个优势类clt≤（t =1，2，…，n）都有；如果是，则令ξ =1，否则，令ξ=0。

步骤3由式（4）、式（5）计算出δ1，t和δ2，t，并取δ1=

步骤4由式（6）、式（7）计算出γ1，t和γ2，t，并取γ1=

步骤5计算出α 阈值平稳区间（a，b] =（δ，α+δ2]∩（γ，α+γ2]。

步骤6判定是否ξ=1，如果是，则输出是相对粗糙规则集，且输出α 的阈值平稳区间（a，b]；否则，输出是绝对粗糙规则集，并输出α 的阈值平稳区间（a，b]。

6 算例

偏好决策系统S=〈U，AT，V，f〉，如表1所示，条件属性集C = {a，b，c，d}，决策属性集D = {e}，fr为频数（总体样本数为50）。

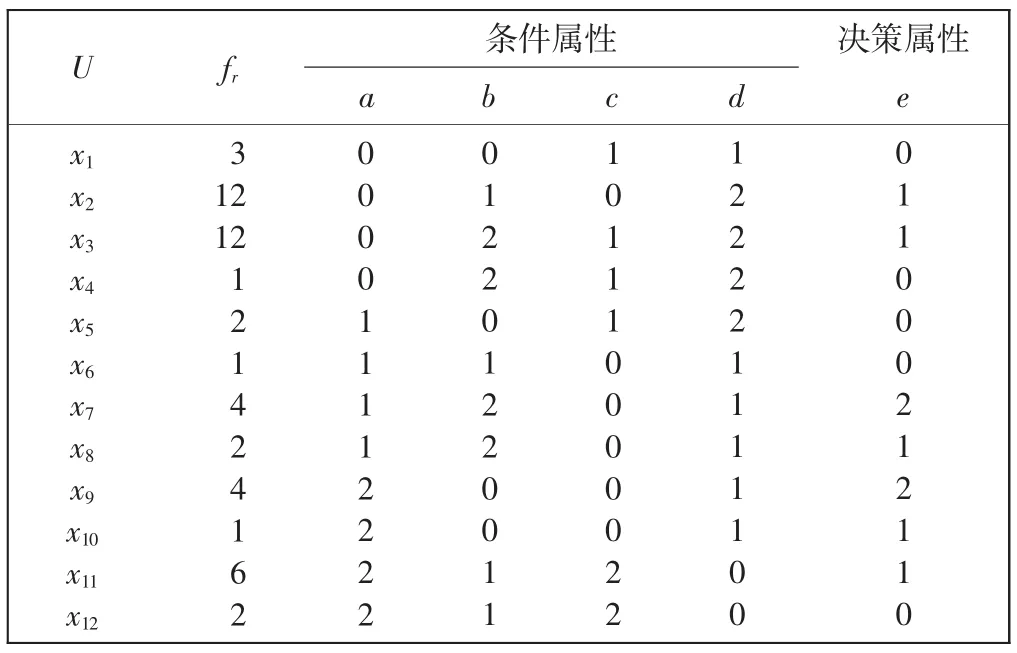
表1 偏好决策表Tab.1 Preference decision table

首先，针对表1利用5.1 节算法求出相对属性约简C*={a，b，d}，再针对向上累积集cl1≥、cl2≥、cl3≥，利用5.2 节算法求得α“至少”一致性规则集，如表2所示，其中取α=0.7。

由于clt≥=U，所以无需保留表2中对应e =0 的“至少”一致性规则，则保留的规则剩下2、4、6、9、11、13、14、16。

表2 “至少”一致性规则表Tab.2 “At least”consistency rule table

对上述保留的α 一致性规则还需进行综合评判，采用设置覆盖度阈值的方法，将一些过于琐碎的规则屏蔽掉，而只保留覆盖度超过阈值的较强壮规则。如若取λ=0.2，则最后保留的规则只剩2、4、6、14。

最后，用于决策的“至少”一致性规则如下：

规则1if a≥0∧b≥0∧d≥1 then e≥1（x∈cl2≥）（准确度为0.83，覆盖度为0.85）；

规则2if a≥0∧b≥1∧d≥2 then e≥1（x∈cl2≥）（准确度为0.96，覆盖度为0.59）；

规则3if a≥0∧b≥2∧d≥2 then e≥1（x∈cl2≥）（准确度为0.92，覆盖度为0.29）；

规则4if a≥2∧b≥0∧d≥1 then e≥2（x∈cl3≥）（准确度为0.80，覆盖度为0.50）。

同样，对于向下累积集cl1≤、cl2≤、cl3≤，利用类似方法亦可求出α“至多”一致性规则集（此处不再赘述）。

此外，通过执行5.3 节算法亦可求得此粗糙规则集是绝对粗糙规则集，且求出的阈值平稳区间为（0.67，0.75]。

7 结语

文中提出一个完整的基于变精度优粗集理论的规则挖掘过程，并通过实例演示证明对于含有扰动数据的优势关系数据集通过变精度优粗集模型进行规则挖掘和知识发现是非常有效的。该方法具有一定的容错能力，能够确保所得到的规则既简洁又具有较高准确度和覆盖度，同时求出了参数对数据集的敏感性区间，便于对实际应用系统进行更加精细地分析。