一种修正I-Quinn的CW脉冲信号频率精确估计方法∗

夏文杰 陆代强 郭晓明 黄 路

（1.国家海洋技术中心漳州基地筹建办公室 厦门 361001）（2.海军工程大学电子工程学院 武汉 430000）

1 引言

低信噪比条件下精确估计CW脉冲信号的频率一直是水声、雷达领域的重要研究内容。已有最大似然估计［1］、相位差分算法［2］和基于离散傅里叶变换（DFT）的各类频率估计等方法。最大似然估计计算复杂度高，难以实时应用，相位差分在低信噪比下效果差，基于DFT的校正方法，运算量小、精度高、实时性好，是一种较稳健且工程易实现的算法。

DFT的频谱校正方法最具有代表性的是Rife插值［3］和Quinn插值［4］，可降低频谱泄露造成的估计误差，但强干扰可能会造成反向插值，导致频率估计误差增大。针对此问题有众多改进算法［5～10］相继提出，估计性能得到一定提升，但低信噪比下，频率估计误差离CRLB还有一定差距。直到一种基于频移性质的I-Quinn算法被提出，解决了当被估计频率位于量化频率附近时估计误差较大问题［11］，该算法对CW信号的频率估计方差较为接近CRLB，但“中心区域”选择不当时，插值后的频率估计误差没有明显降低，本文在该算法的基础上，使用两次Quinn插值，省去选取中心区域步骤，进一步提高了频率估计精度。

2 CW信号频率估计

2.1 Quinn插值法

Quinn插值法频率估计公式为

式中，Δf为频率分辨率，k0为DFT最大谱线的索引值，δ∈[-0.5，0.5]为频率偏移值，其表达式为

根据式（1）～（4）可实现CW信号中心频率估计。Quinn插值法的理论频率估计方差为［12］

根据上式可知，随着|δ|的增加，估计方差单调减小，当|δ|接近0.5时，估计方差较小。

2.2 I-Quinn插值法

Quinn算法在低信噪比或|δ|较小时，会产生较大的估计误差。为了降低|δ|较小时频率估计误差，结合频移性质，I-Quinn算法被提出：首先，对接收信号用Quinn算法估计频率偏差δ，判断其是否位于中心区域，若δ位于中心区域，直接用Quinn算法进行频率估计；若δ位于中心区域之外，那么先对接收信号进行频移得到新的信号，之后，使用Quinn算法实现频率估计。I-Quinn插值算法的整体性能优于之前的同类算法，I-Quinn算法步骤如下。

1）对接收信号x（n）进行Quinn插值，得到频率估计值和频偏值估计值δ0。

2）根据式（5）选取实际中选取中心区域 (u，λ)，一般取值u=0.35，λ=0.5。判断条件“u≤|δ|≤λ”是否成立。条件若为真，将作为频率的最终估计值，否则，执行步骤3）。

3）对接收信号x（n）进行频移，频移后新信号表示为

式中，δk=0.5-|δ|为频移因子，αk=sign(δ)，为频移方向。

4）同样，对新的信号进行Quinn插值，计算新的索引值ks和频偏δs，计算最终的频率估计值book=154,ebook=160=Δf(ks+δs-αkδk)。图1为I-Quinn算法流程。

图1 I-Quinn算法流程

2.3 修正I-Quinn算法

I-Quinn算法在中心区域的选取上没有进行理论分析，随意选取中心区域不能使算法性能达到最佳。这里对I-Quinn算法进行修正，根据式（5）可知，当|δ|越大，频率估计误差越小，通过比较|δ0|与|δs|的大小，来确定频率估计值。

若|δ0|>|δs|，最终频率估计值为；反之，估计值为，图2为修正I-Quinn算法流程。

图2 修正I-Quinn算法流程

修正I-Quinn算法使得频率估计方差更接近CRLB［1］：

3 仿真实验

仿真实验具体参数如下：信号为复CW波（实CW信号的误差是复信号的两倍），采样频率fs=64kHz，采 样 时 间 T=16ms，频 率 分 辨 率Δf=62.5Hz。图3（a）、（c）为信噪比为-3dB和3dB时，不同中心频率的估计的均方根误差，频率选取[104Δf-Δf/2，104Δf+Δf/2]区间内等间隔的41个频率。当频率偏差δ的绝对值偏离0.5时，I-Quinn及其修正算法的均方根误差（Root Mean Square Error，RMSE）接近CRLB，明显优于Quinn算法；当频率偏差δ的绝对值接近0.5时修正I-Quinn算法性能要优于I-Quinn算法。

图3 不同频率的均方根误差

图4为多种插值算法在不同信噪比下估计的均方根误差，其中还包含Rife算法和M-Rife算法［18］。图4（a）中设置信号频率f0=104Δf+0.45Δf，此时这5种算法的均方根误差都较小。图4（b）中设置信号频率f0=104Δf+0.05Δf，只有I-Quinn算法及其修正算法误差接近CRLB，其余三种算法误差都偏大，与理论相符合。

图4 不同信噪比的均方根误差

由于I-Quinn算法及其修正算法性能在图4中不易区分，难以只比较修正I-Quinn算法和I-Quinn算法差异，为了能够更直接显示算法性能，特列表1。从表1中可知，修正I-Quinn算法的RMSE比I-Quinn算法要小，基本已经接近CRLB。

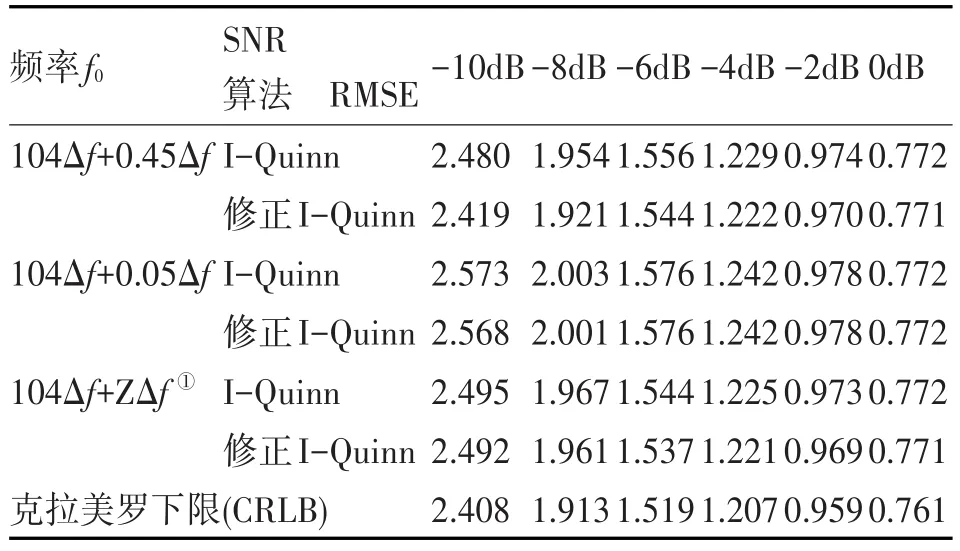
表1 I-Quinn和修正I-Quinn算法均方根误差

4 结语

本文针对CW脉冲信号中心频率估计问题，深入研究了DFT的频谱校正方法。I-Quinn算法将频移技术和Quinn算法在被估计频率位于相邻量化频率中心点时频率估计精度高的优点相结合，具有稳定频率估计性能。针对目前性能最佳I-Quinn插值算法，对其中频移准则的中心区域进行修改，提出了提出修正I-Quinn插值算法。

从仿真实验结果可以看出，修正I-Quinn算法相比于各类插值算法，在全频段频率的频率均方根误差更接近克拉美-罗下限，具有良好的估计性能。特别是在低信噪比且估计频率位于量化频率中间时，性能提升明显。