技术创新和人力资本对区域经济的动态影响
巫媛莹
(中山大学附属第三医院,广州510630)
经济增长一直是世界各国永恒的话题,对于发展中的中国更是极其重要。中国现阶段不同区域经济发展程度差异显著,因此,探究影响区域长期经济增长的影响因素以及这些因素之间的动态关系是亟待解决的重要研究问题。已有的研究已经在理论上指出技术进步、技术创新和人力资本是推动国家和区域经济增长的重要内生因素,但是实证研究却未给出一致的研究结果。并且,少有研究将技术创新和人力资本结合起来探究两个因素对区域经济增长的动态关系,以及技术创新和人力资本的动态均衡路径。研究将通过构建内生增长模型对这一问题进行系统、全面的研究。
为分析技术创新和人力资本的内生过程以及对于区域经济增长的影响,在内生增长模型的基础上建立新经济内生增长模型,探究人力资本和技术创新对于经济增长的影响。
一、内生增长模型构建
(一)生产方程
柯布道- 格拉斯(C-D)生产函数是最为广泛应用到经济增长研究的表达形式。研究在此基础上建立两阶段内生增长的模型(经济增长模型与技术创新模型)进行扩展,并且将人力资本引入生产函数,将其设定为:
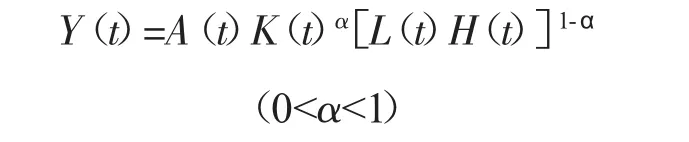
以上公式中,Y(t)是区域经济的总产出(GDP),A(t)是区域经济中的技术水平或技术能力,K(t)是区域经济中资本存量,L(t)是区域经济中劳动力的数量,H(t)是区域经济中人力资本的数量。
假设区域经济中劳动力增长速度是外生变量,劳动力以n 的速度稳定增长。劳动力增长方程:假设区域资本存量的增长是来源于区域经济的总产出的存储量与上期资本折旧的差值。此外,假设区域经济中储蓄率固定不变为s,折旧率固定不变为δK。
L(t)=nL(t)
资本增长方程:
K(t)=sY(t)-δKK(t)
(二)技术创新方程
技术创新的增长同样采用柯布道格拉斯(C-D)生产函数的形式表达。技术创新的增长来源于对技术创新的资本投入、劳动力投入、人力资本和上期技术水平,将其设定为:
A(t)=KA(t)β[LA(t)HA(t)]γA(t)θ
上式中KA(t)表示对于技术创新的资本投入,β表示资本对技术创新的影响,假设不存在规模效应,因此0<β<1。LA(t)和HA(t)分别表示对技术创新的劳动力投入和人力资本投入,表示劳动力和人力资本太投入的转化率,γ 同样假设不存在规模效应,因此0<γ<1。A(t)表示区域经济的技术水平,θ 表示区域技术水平对于技术创新的影响,0<θ<1。
(三)人力资本增长方程
人力资本来源于对劳动力的投资,主要包括对劳动力的教育和培训等方面。区域经济水平将会影响对于劳动力的教育和培训,区域总体劳动力数量将影响人力资本数量。因此,区域经济总量和劳动力数量影响区域人力资本的增长。此外,人力资本与资本存量的相似,同样存在资本折旧,人力资本的折旧主要源于劳动力年龄的增长,在研究中假设区域经济中人力资本以固定不变的比例折旧。
H(t)=BY(t)m-(δH-n)H(t)
上式中B 为区域经济人力资本增长的固定常数,因为区域的不同,人力资本的增长速度存在固定的差异。其中m 为区域经济总量转化人力资本的影响系数,δH为人力资本的折旧率,(0<δH<1)表示劳动力随年龄增长的折旧,n 为区域劳动力增长率,人力资本的折旧与劳动力的增长可以有效反应人力资本动态变化。
(四)增长稳态方程
将区域经济增长方程代入资本积累方程得:
K(t)=sA(t)K(t)α[L(t)H(t)]1-α-δKK(t),
变量的增长率等于该变量自然对数的变化率,即
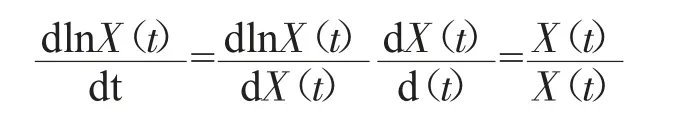
将资本积累方程两边同时除以K(t)
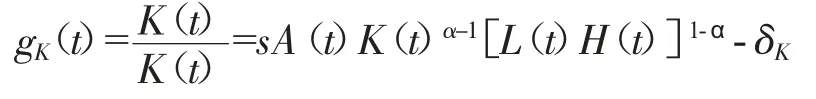
上式中gk(t)表示K(t)的增长率,也就是资本存量增长率的增长率。将资本折旧率δK移到左边得:
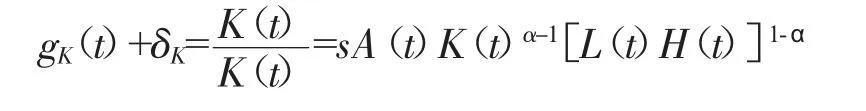
将上公式两边取自然对数得:
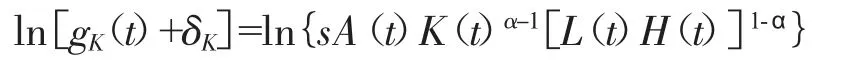
将上公式右边各变量分开得:
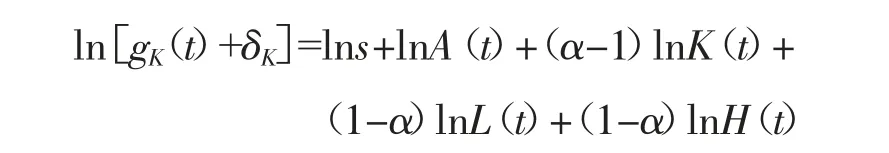
再将公式两边取自然对数,并且关于时间t 求导数得:
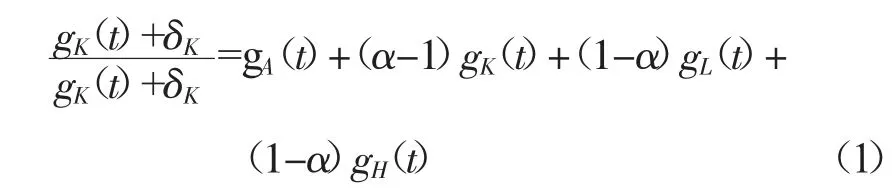
类似,将技术创新方程两边同时除以A(t)
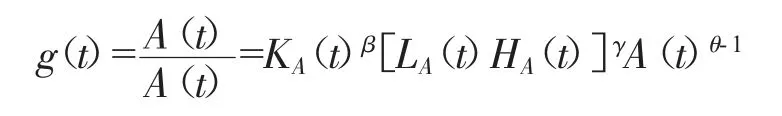
并且取自然对数得:
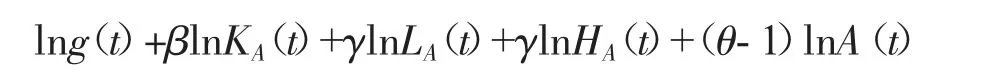
然后关于时间t 求导数得:
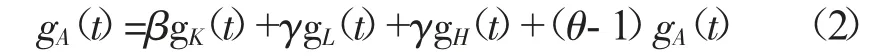
此外,将经济增长模型代入人力资本增长模型中得:
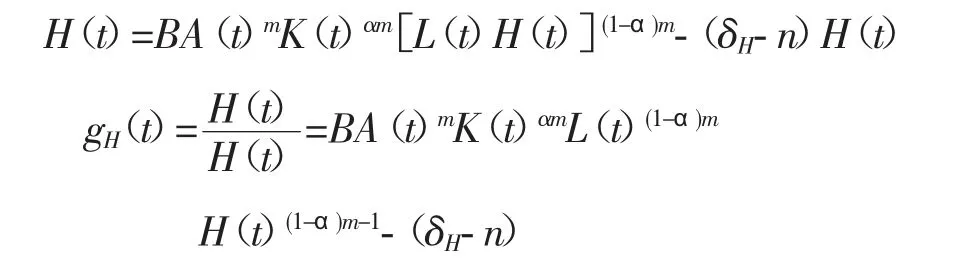
将上公式中等号右边的常数项移到左边,并且公式两边取自然对数得:
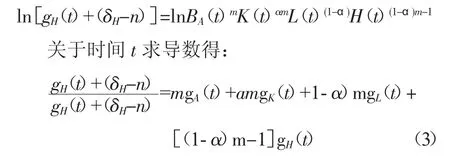
公式(1)(2)和(3)构成关于gK(t)、gA(t)和gH(t)的非线性动力系统。gK(t)、gA(t)和gH(t)以稳定的速度增长,所以gK(t)、gA(t)和gH(t)的变化速率应该保持不变,公式(1)(2)和(3)的右边等于零,整理公式得:

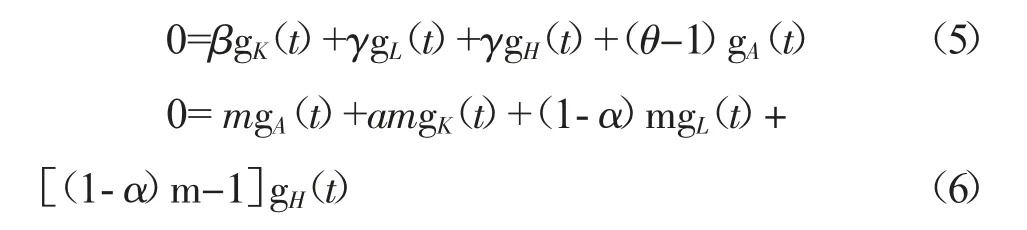
其中,gL(t)=n,联立公式(4)(5)(6)得到稳态方程:
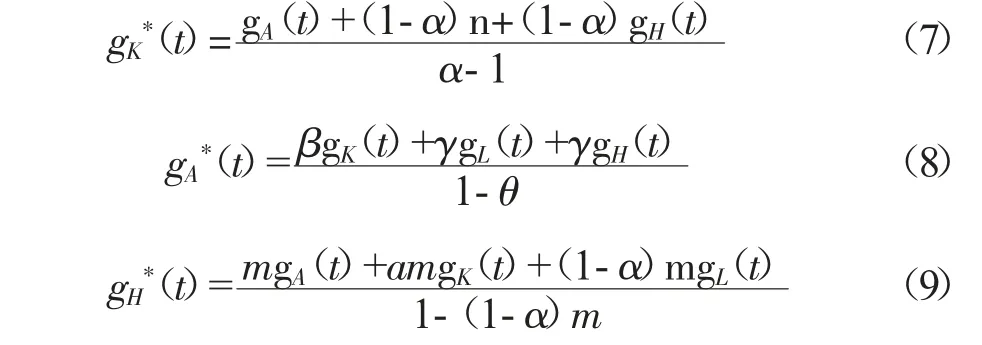
公式(7)(8)和(9)构成了经济稳定增长时的系统稳态方程组。有助于了解资本积累、人力资本和技术创新对于区域经济增长的影响。
对经济增长方程两边同时取自然对数得:
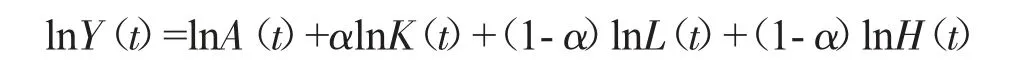
然后方程两边同时对于时间t 求导得:
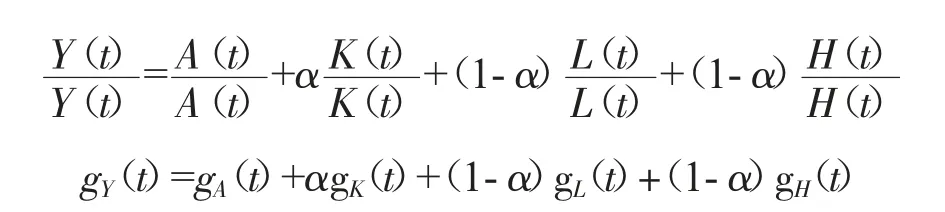
将稳态方程(7)(8)(9)带入以上方程可以得到经济增长率方程:
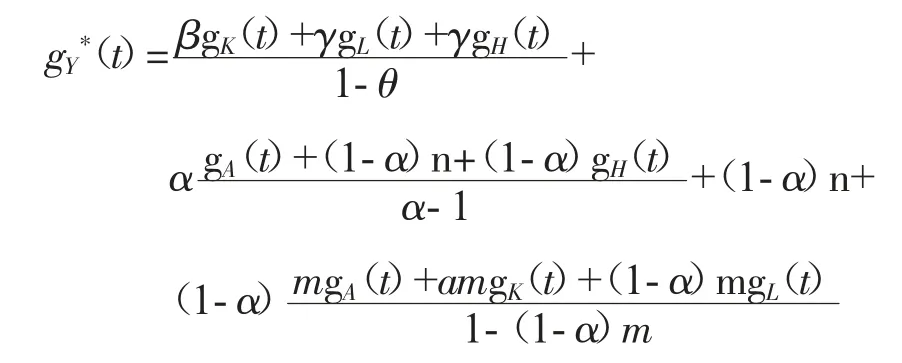
以上就是经济稳定增长时,资本积累、人力资本和技术进步之间的平衡关系。技术创新的增长率受到资本和人力资本的制约,与此同时,人力资本的积累也受到技术创新的限制,因此,人力资本积累和技术创新之间的关系是相互制约、相互促进。此外,从以上公式还可以得出,在劳动力增长率既定的前提下(gL(t)=n)区域经济稳定增长率gY*与资本积累增长速度gK、人力资本积累速度gH以及技术创新增长速度gA成正向的线性关系,随着gK、gH以及gA的变化,区域经济增长率也随之变化。
二、研究总结和启示
研究在内生增长模型基础上,同时添加区域人力资本和技术创新因素,并且将人力资本因素添加到技术创新过程中,建立新人力资本—技术创新—区域经济内生增长模型,探究区域人力资本和技术创新对于区域经济增长的影响以及之间的动态均衡关系。通过模型分析可以看出,区域人力资本积累和区域技术创新增长之间相互制约、相互促进。当两者动态均衡时,区域经济将长期、稳定增长。
研究的主要贡献有以下几点:第一,通过构建两阶段内生增长模型探究技术创新和人力资本对区域经济增长的动态影响过程,以及非线性动力系统揭示区域经济稳定增长时技术创新和人力资本的均衡路径。通过模型分析得出,区域人力资本积累和区域技术创新增长之间相互制约、相互促进。当两者动态均衡时,区域经济将长期、稳定增长。尽管有大量文献分别探究人力资本和技术创新对于经济增长的影响,但是少有文献同时探究两者之间的动态均衡关系,以及对于区域经济增长的影响。研究通过构建内生经济增长模型,探究人力资本和技术创新对于区域经济增长的影响,补充先前的研究不足。第二,尽管已有文献研究人力资本对于经济增长的影响,但是这些研究都是探索人力资本的直接影响,而忽略人力资本对于技术进步的影响,进而技术进步影响经济增长的传导机制。研究在实证模型中建立两阶段生产—技术创新方程,分别探究人力资本对技术创新和区域经济增长的影响,补充已有研究的不足。

