门式起重机速度与摆角的耦合研究

庞振华，刘 放，唐 语，吴 涛

（西南交通大学 机械工程学院，成都 610031）

0 引言

目前，大部分港口、工厂、车间都在向自动化方向发展，在未来工业自动化也将是主要的发展方向。要发展自动化，起重机起到了至关重要的作用，然而起重机的摇摆仍然是目前需要解决的主要问题之一。抑制起重机的摇摆能有效的提高其工作效率，能更好的促进工业自动化的进程；并且抑制起重机的摆动保证工业系统的安全运行。

国内外有许多学者对此进行了研究并且取得了相应的成果[1]。目前的防摇措施主要有机械防摇和电子防摇。在机械防摇上，吴俊杰，吉阳，等采用吊盘式机械防摇方案[2]；Ho-Hoon Lee采用在运动过程中改变绳长[3]，研究结果表明，上述防摇方式能有效的抑制吊重的摆动。在电子防摇方式上，张圆圆，何永玲等采用模糊控制算法[4]，通过模糊控制规则进行控制；梁成，刘放，等采用PD控制[5]；赵华洋，李理，等采用神经元控制的方法对起重机进行防摆研究[6]，Aydin Yesildirek采用基于切换Lyapunov函数的非线性控制器[7]。LEAT，MOON S C等采用自适应滑膜控制对不同长度的缆线造成的稳定性进行了研究[8]，周奇才，王璐，等研究弹性起重机防摇[9]。

为了改善起重机在运动过程中的摇摆问题，本文提出了一种速度、摆角的双PI控制方法。通过仿真软件计算出无防摇控制下，起重机的自由摆动。最后分析了两种启动方案对所提出的控制方法的影响。

1 建立起重机动力学模型

1.1 建立抽象模型

将起重机实际模型进行抽象处理（如图1所示），在笛卡尔坐标系中，小车与重物连在一起，小车受驱动力可在横梁上自由运动，重物在小车运动情况下进行自由摆动。该系统可通过两个广义坐标变量来描述，小车相对于原点O的距离为x，重物摆动角度与中心线夹角为θ。

在本次研究中忽略钢丝绳与小车之间的阻尼；忽略钢丝绳的质量。

图1 起重机抽象模型

1.2 建立动力学方程

小车在驱动力F的作用下移动，重物随之进行自由摆动，小车与横梁之间的阻尼系数为c。利用拉格朗日方程建立系统的动力学方程[10]：

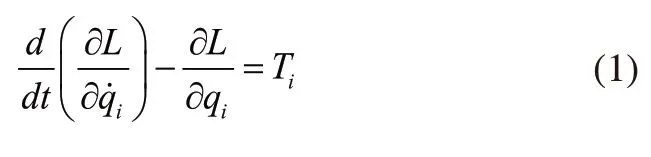
其中L是拉格朗日函数，由于该系统为2自由度模型，故qi（i=1，2）是两个广义坐标变量。q1代表的是小车的位移x，q2代表重物摆动角度θ。Ti代表系统外力，若系统仅有保守力做功，则Ti为0。L可以描述为：

其中K是整个系统的动能，P代表系统的势能。

系统的动能有两部分组成，第一部分为小车的动能，第二部分为重物的动能。小车的速度为沿横梁移动的速度，重物的绝对速度为重物随小车的牵连速度ve和重物绕小车中心转动的相对速度vr的合速度，如图2所示。

通过几何关系可得：

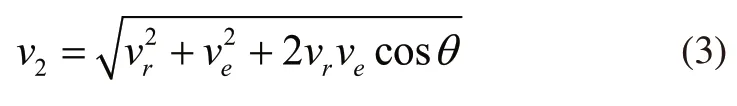
其中v1为小车的绝对速度，v2为重物的绝对速度；重物的牵连速度ve=v1；相对速度

系统动能K：

系统势能P：

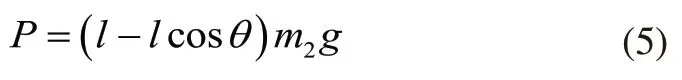
拉格朗日函数L：

图2 速度合成图

将式(6)代入拉格朗日方程得：

上式中：m1为小车质量；m2为重物质量；c为小车与横梁之间的阻尼系数，x为小车的位移，F为小车所受的驱动力；l为钢丝绳的长度；θ为重物的角位移。

将上述数学模型写成矩阵形式：

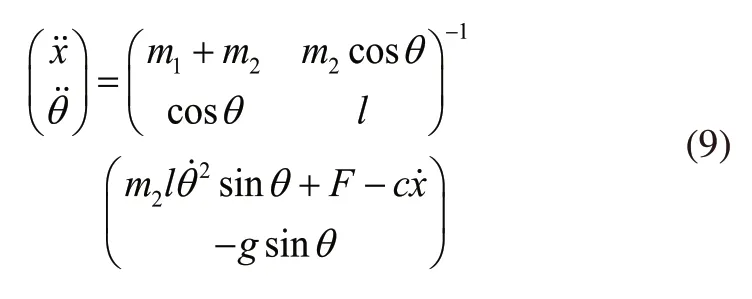
2 控制算法

PID控制器是一种线性控制器，它根据给定值ri与实际值输出值yo构成控制偏差：

PID控制规律为：

式(11)可以写为：

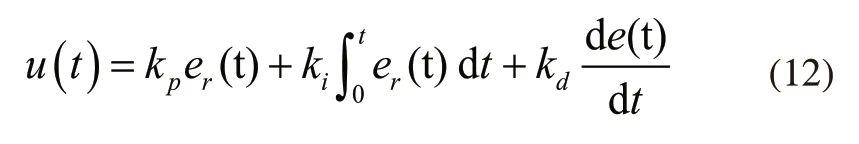
式中：ki=kp/Ti为积分增益；kd=kpTd为微分增益。

本文研究两种小车启动方式对起重机控制系统的影响。两种启动方式采用相同的控制原理，不同点在于施加驱动力的方式。第一种方式是先施加恒定的驱动力，达到一定的速度之后再采用控制算法降低重物的摆动角度；第二种方式是直接采用控制算法控制小车达到设定速度并降低重物摆动角度。

图3 控制框图

该起重机控制系统采用的控制方法如图3所示，采用两个控制器控制，其中速度控制器将小车运动速度稳定在参考值附近；角度控制器将重物的角位移控制在极小的范围内。

3 模型仿真与数据分析

选取适当参数代入上述动力学方程，各参数选取结果如表1所示。Simulink和MATLAB优化工具箱用作仿真平台。

表1 仿真参数

3.1 无控制下重物摆角变化

下图为小车在无阻尼情况下施加恒定驱动力，加速一段时间后取消外力时重物摆角的变化（如图4所示）。图中的3条曲线代表小车运动时重物摆动情况，每条曲线所代表的小车的加速时间不同。

曲线1代表小车在10N的驱动力下加速1s得到的重物摆动曲线。在t=0.5s的时刻，重物摆角出现最大值，摆角大小约为0.225rad，最大振幅仅出现一次。在加速1s之后，小车保持直线运动，上下振幅有所减小，振幅约为0.103rad。由于钢丝绳与小车之间的连接没有阻尼存在，因此在小车直线运动阶段重物进行等幅振荡。

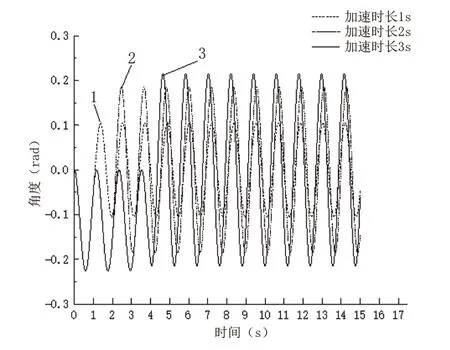
图4 重物自由摆动

曲线2代表小车在相同驱动力下加速2s，重物自由摆动的曲线。在小车加速过程中，重物出现了两次的最大振幅，振幅大小与曲线1中的最大振幅接近。在2s之后，小车保持直线运动，重物在小车运动过程中进行等幅振荡，振幅大约为0.185rad。

曲线3代表的是小车加速3s，重物在钢丝绳的牵引下自由摆动曲线。小车在加速过程中，重物在-0.25～0rad之间摆动，其中最大摆角为-0.223（rad）。加速过程结束后，小车保持直线运动，同时重物开始进行等幅振荡，振幅为0.215rad。

综合3条曲线分析，小车在加速过程，重物摆动的振幅大小基本相同，同时也是运动过程中的最大振幅，并且重物仅在θ<0的范围内摆动。当加速过程结束，小车保持直线运动，由于重物的存在，小车速度在一定范围内振荡。加速1s，小车速度约在1.1m/s附近上下振荡；加速2s，小车速度约在2.3m/s附近上下振荡；加速3s，小车速度约在3.4m/s附近上下振荡。

重物在无外部激励下保持等幅振荡，但是3次仿真结果的振幅大小不相同。通过图4可知，匀速情况下振幅大小与加速时间相关，小车加速结束时刻重物所在的位置影响重物后续摆动的振幅，但是3种情况下摆动周期相差不大。

3.2 无驱动力情况下，小车和重物加速度和摆角变化

当小车在原点时，直接给控制器输入控制信号，控制小车和重物运动。本次研究3种参考速度下小车的运动情况和重物摆动规律。

图5表示的是控制器设定的参考速度分别为1.1m/s，2.3m/s，3.4m/s的情况下，重物摆角随时间的变化。曲线1代表控制系统中的参考速度为1.1m/s时，重物摆动情况；曲线2代表参考速度为2.3m/s时，重物摆动情况；曲线2代表参考速度为3.4m/s时，重物摆动情况。

参考速度为1.1m/s的情况下，小车的加速时间大约为5s，在此段时间内，重物产生不规则振动，摆角的最大值约为0.13rad，出现最大摆角的时刻约为0.5s。在小车的加速过程中，重物振动的振幅逐渐衰减，大约6s之后，振幅衰减到0rad，小车以1.1m/s的速度做匀速直线运动。

图5 重物摆角变化

曲线2和曲线3分别表示参考速度为2.3m/s和3.4m/s时，重物摆动的规律。曲线2的最大摆角出现在0.58s，最大摆角为0.30rad；曲线3的最大摆角出现在0.64s，最大摆角为0.45rad。这两次控制时间与第一种情况相似，重物摆角都在大约6s之后稳定到0rad，并且重物的振动都在逐渐衰减。虽然3种情况下最大摆角相差较大，但是都能在1s之后快速衰减到可接受的范围内。

当参考速度为2.3m/s和3.4m/s时，控制系统为了使小车快速到达设定速度，系统会在刚开始的时候给小车一个较大的驱动力从而产生很大的加速度（如图6所示）。当参考速度为2.3m/s时，最大加速度为7.7m/s2；参考速度为3.4m/s时，最大加速度为11.3m/s2。因此系统会产生较大的冲击。

3.3 施加驱动力后，小车和重物加速度和摆角变化

小车在启动过程中先采用恒定驱动力启动，当加速到一定速度之后再采用PID控制算法将小车速度控制在预期值，并抑制重物的摆动。图7展示了上述情况下重物摆动角度的变化。

图6 小车加速度变化

图7 重物摆角变化

如图7所示，曲线1为施加1s恒定驱动力的重物摆动曲线；曲线2为施加2s恒定驱动力的重物摆动曲线；曲线3为施加2s恒定驱动力的重物摆动曲线。3条曲线大约在0.47s出现最大值，最大摆角为0.22rad，而且3种情况下最大值相同，这是因为前1s内小车在恒定驱动力下运动。从图7可以看出，在恒定驱动力结束之后，控制系统能迅速的将重物摆动的角度抑制在极小的范围内，控制期间的最大摆动角度约为0.04rad。由于加速时间不同，抑制重物摆动的时间略有差别。曲线1停摆时间约为6s；曲线2停摆时间约为7s；曲线3停摆时间约为8s.若不考虑恒定驱动力的加速时间，重物停摆时间相差不大。

如图8所示，小车在3种情况下小车在0时刻的加速度最大，加速度最大值约为3.3m/s2，之后小车加速度的峰值越来越小。小车的最大加速度是由恒定驱动力产生的，在控制阶段，小车的加速度明显降低，并且快速稳定到0m/s2。

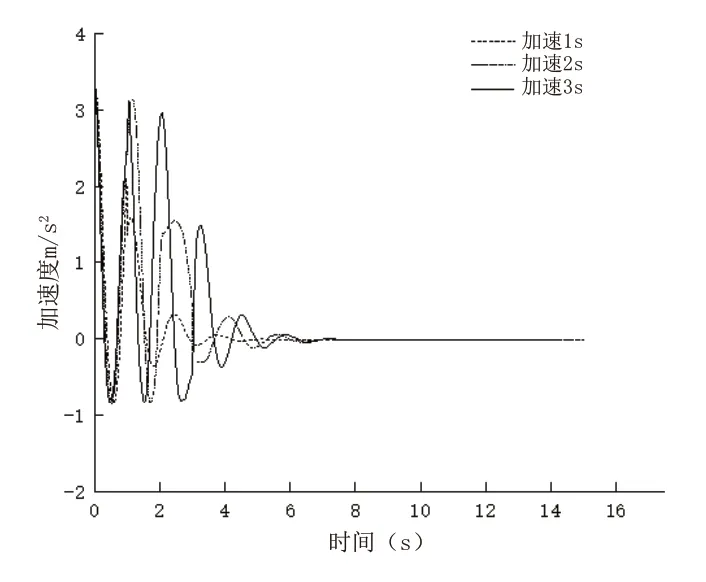
图8 小车加速度变化

4 结语

根据仿真数据可以看出，本文提出的控制算法在两种情况下启动都能很好地控制小车的行驶速度，同时能有效的抑制重物的摆动。

小车匀速运行速度较低时，完全由控制器控制小车的启动，能有效的降低重物的最大摆角，并且系统能快速到达稳定状态。

小车匀速行驶的速度较高时，完全由控制器控制小车的启动会显著增加重物的最大摆角，并且小车会受到较大的柔性冲击。先施加恒定驱动力后在采用控制器能有效的减小重物的最大摆角和小车的柔性冲击。