基于PowerPC 架构的波束指向算法的优化
雷淑岚,吴会祥,李文学
(中国电子科技集团公司第五十八研究所,江苏 无锡214063)
0 引言
波束指向算法主要完成在已知卫星大地坐标系的经度、纬度、高度(long、lati、heig),无人机大地系坐标系的经度、纬度、高度(long、lati、heig),飞机俯仰角、横滚角、航向角(p、r、y)的情况下,天线阵面中心在机体直角坐标系中的位置(Xb、Yb、Zb),计算卫星在天线球坐标系中的方位角、俯仰角(θ、φ),从而进行收发天线的波束对准[1]。 本文主要是基于PowerPC460 架构处理器对波束指向算法进行合理的优化,以期在算法的实时性处理上有所优化。 本文从四个方面对波束指向算法进行优化:(1)基于CORDIC 算法设计的硬件电路实现三角函数的速算优化;(2)浮点数运算的优化;(3)循环嵌套优化;(4)基于PowerPC 指令集的优化。
1 基于CORDIC 算法设计的硬件电路实现三角函数的速算优化
1.1 CORDIC 算法原理
在传统的硬件算法设计中,乘、除等基本数学函数运算是一种既耗时又占用面积大的运算,甚至有时是难以实现的,CORDIC 算法正是为解决这种问题而产生的。它从算法本身入手,将其分解成为一些简单的且在硬件中容易实现的基本算法,如加法、移位等,因此使得这些算法在硬件上可以得到较好的实现。 又由于该算法是一种规则化的算法,它满足了硬件对算法的模块化、规则化的要求,因此CORDIC 算法可以充分发挥硬件的优势[2-3]。 利用硬件的资源,从而实现硬件与算法相结合的一种优化方案,正是由于上述原因,CORDIC 算法的原始思想一经提出,就受到了人们的普遍关注,40年来人们不断地对其进行探索研究,并提出了各种改进算法和优化方案以适应各种不同的需求[4-11]。
在处理数字信号过程中,由于三角函数发生器在高速和高精度方面特点使得其有着较为广泛的使用范围。而相对于传统的方法实现多为采用查表、多项式展开或近似的方法[12-14],但是带来问题是速度、精度、简单性和高效方面做的不好。 而用CORDIC 算法实现的三角函数发生器能很好地兼顾这几个方面,因此对于VLSI 的实现就显得非常适合[15]。 下面简要介绍一下CORDIC 算法的计算流程。
CORDIC 算法是一种迭代的算法,把所需旋转的角度分解成N 步去完成,每一步的迭代方程如下:
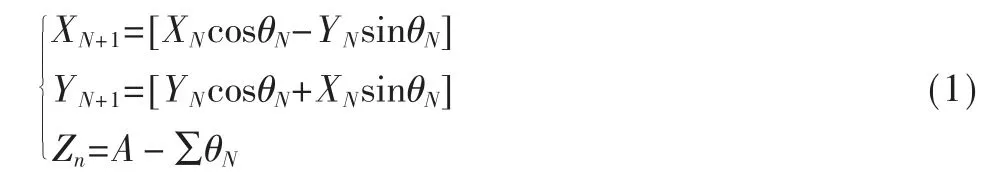
迭代次数一般人为控制,限制范围是Zn足够小,精度已经达标。
迭代完成后的方程可以表示为:
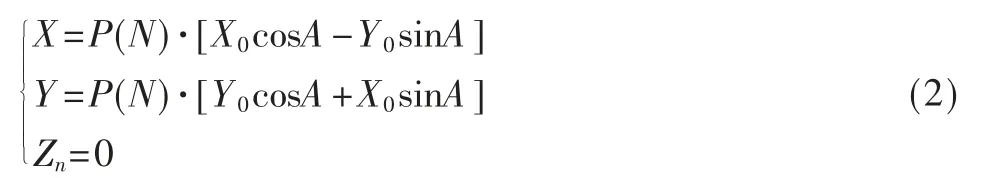
其中P(N)是每一步迭代中提出项cosθN的累积值,求极限可以得到这个累计值是P(N)≈0.607 253,若取X0=1/P(N),Y0=0,A=θ,则从上式可以推出:

1.2 CORDIC 算法可以用以下两种硬件结构来实现
CORDIC 算法的最简单最容易想到的实现方式是反馈结构。 这种结构只设计一级流水,将系统输出反馈到输入进行迭代运算。迭代次数和移位位数通过控制命令来实现。 这种结构硬件开销比较小,但可想而知比较耗时,在实时性要求很高的系统上,比如卫星导航系统,就不太合适了。
第二种可能实现的结构是流水线型。 这种流水线的思想主要是为了满足实时性的要求。每一级迭代都是一级流水线,移位的位数等于本级流水线的级数,顺时针还是逆时针可以通过Zn的最高位来判断,0 的时候是顺时针,1 的时候表示逆时针。 每一级迭代的结果就是下一级流水线的输入。进过N 级流水线后的输出结果:Zn=0(满足精度要求的情况下,趋向于0),X 和Y 的值就是输入的旋转角度的正弦值和余弦值。
如果选择迭代15 次,则硬件上需要设计一个16 级流水线的结构,字长是19 bit,最高位为符号位,i 的初始值是1。 流水线结构可以设计成如图1 所示。

图1 CORDIC 流水线结构
由于在波束指向的算法处理中,坐标系之间的变换最常见的运算就是正弦函数和余弦函数的计算,传统的计算方式用的是幂级数展开的方式,是基于纯软件的运算,如果可以使用上述的流水线硬件结构来计算正弦值和余弦值,那算法处理的速度将会大大提高。
2 运算浮点数的变型和位数的控制
对浮点数而言,波束指向算法要求达到的精度是小数点后三位, 单精度浮点数小数点后有效数字是6~7位,双精度浮点数小数点后有效数字是15~16 位,所以运算过程中,使用单精度型浮点数已经可以达到要求。对于在算法中出现的浮点数的乘除运算,可以将浮点数转换成整型数进行计算,以提高运算速度。 计算出结果后再通过反向移位还原到正确结果。 举例说明如下:

俯仰角一般是单精度型的浮点数,有效位数在小数点后三位,那么在运算之前可以将pitch 乘以1 000,化成整型数再进行计算。 在计算完成之后,运算结果再除以1 000。 整型数的计算比浮点数运算要快得多。
3 循环嵌套优化
循环嵌套优化是将具有相同循环变量和循环次数的循环体嵌套,在一个循环里完成循环,这样可以大大减少因循环占用的时间消耗,举个例子如下所示:


优化前找到满足条件的航向角和横滚角需要2×9个循环,优化后只需要一半的循环次数就找到了满足要求的航向角和横滚角。
4 基于PowerPC 指令集的优化
基于PowerPC 体系的CPU 种类很多,优化也是建立在对环境很了解的基础上。 比如基于CORDIC 算法设计的硬件电路如果选择第二种流水线结构,习惯上,主频越高,流水线越长,速度就越快,处理性能也越好,但在PowerPC 的环境下,流水线的长度和分支预测失误代价是成正比的,单条指令执行效率也会随之降低。 CPU 一般根据应用场合不同采取不同的优化策略:科学性计算机、商务型计算机和多媒体型计算机。 而对于科学性计算机来说,采用的是小而密集的循环计算。 应用场合不同,优化策略也不同。 PowerPC460 内核的体系是短流水线型,主频虽然低,但处理速度却惊人。下面从四个方面来阐述指令优化的原则和方法。
4.1 指令相对原则
PowerPC 的环境下有三种指令的类型,PowerPC 的系统能够在一个周期内执行完两种不同类型的指令:
(1)加载或存储数据的指令;
(2)设置CR 寄存器进行比较,分支,乘除SPR 寄存器更新;
(3)其他种类操作:非SPR/CR 寄存器更改,算术与逻辑。
PowerPC 体系下对指令执行的这个原则就使得如果相邻两条指令是同一类型,第二条就必须要等到第一条执行结束才能执行,这样就浪费了一个时钟周期,所以在写汇编语句的时候,就要注意把两条相同类型的语句隔开,以达到最大的执行效率。 在某些体系的流水线结构中,相邻两条语句如果是无依赖的代码都可以并行执行,但在PowerPC 的体系下,无依赖的指令若属于同一类型,仍然不能并行执行。举个例子,整数计算指令属于同一类型,载入指令属于同一类型,如下语句混合写才最有效率:

4.2 加载依赖原则
PowerPC 体系下,数据从缓存中被加载到寄存器里再到被其他语句调度,至少需要等两个周期,也就是说在加载数据到寄存器后,第三个时钟周期才能使用该寄存器里的数据,这样就可以利用中间两个周期的真空期做一些优化。 根据第一个指令相对原则,两条不同类型的指令可以在同一个时钟周期内被执行完成。 这样,在这段真空期里,就可以放置最多5 条指令。 在实际使用中,具体能放置的指令数同样取决于这些指令类型的混合顺序,最少也能放置两条指令。
有一些具有更新功能的加载指令,比如lwzu 这个指令,这个指令不但能加载数据到目标寄存器,同时也能更新源寄存器。所以,在使用这个指令的时候,要等到两个周期后才能对源寄存器里的数据进行调度。
4.3 指令依赖原则
如果两条指令有上下文的依赖关系,那这两条指令就不能在同一个时钟周期内被调度,也就是说,如果第一条指令调度的寄存器被第二条指令使用了,那第二条指令一定会在第一条指令执行完成后才能被执行,这样,就可以在两条指令中间放置一条指令来填补这个时间差。
举个例子来说,周期k 内,执行了add r4,r5,r6 这个语句,这个语句里更新了r4 寄存器,那在周期k 内,就不能再执行任何与r4 寄存器有数据交换的动作,比如srawi r7,r4,4 指令,必须要等到k+1 周期内才能被执行,这样就可以在两条指令中间添加一句lwz r3,0(r10)语句,就可以把这个时间差填补了,这样程序执行起来更有效率。
4.4 缓存优化原则
CPU 在从主存里取数的时候,工作原理是先把主存加载到缓存中,然后在缓存里对数据进行处理,最后才把数据更新到主存里。 根据加载依赖原则可以得知,数据从缓存中加载到寄存器里需要等待三个周期才能被再次调度,也就是说如果CPU 想使用某个主存地址里的数据, 那它就要先把主存地址里的数据加载到缓存,然后才能把缓存里的数据加载到寄存器里,这样等待周期就超过了三个周期。 所以,现在的PowerPC 体系为了减少从外存加载到缓存的时间,都使用了一个DCBT(Data Cache Block Touch)的指令:
DCBT rA,rB: 将rA 和rB 地址里的数据预先存储到缓存里。
这个指令的作用是提前告诉CPU 程序要使用哪块内空间的数据,CPU 先把这块数据加载到缓存里,过段时间等用到这个数据的时候,就不用再浪费时间从内存里加载到缓存上。
举个例子来总结一下PowerPC 体系下上述几个优化原则的使用,如下所示:

上述代码使用到的三种优化是:
(1)缓存预读取;
(2)多寄存器并行使用;
(3)非同类型指令同周期执行达到并行处理的效率。
在波束指向算法中,C 代码的执行效率不如汇编语言高,但在满足实时性要求的基础上,并不需要对通篇代码进行汇编改写,这里选取C 代码里耗时最长的天线选择函数进行汇编改写, 并使用上述指令集的优化原则,以期达到最高的执行效率。因代码过长,现提取部分代码如下所示:
# 找到旋转俯仰角最小的天线编号


5 优化结果分析
在50 MHz 时钟频率的JS71232 芯片环境下,编译优化等级选择-O2,通过在程序里添加set_time_base(0,0)和get_time_base(&Tbu,&Tbl)的指令,来测试程序的运行的时钟周期。表1 是不使用优化的程序实测时间和使用各种类型优化的实测时间,已将耗时转换成以毫秒(ms)为单位的计时。
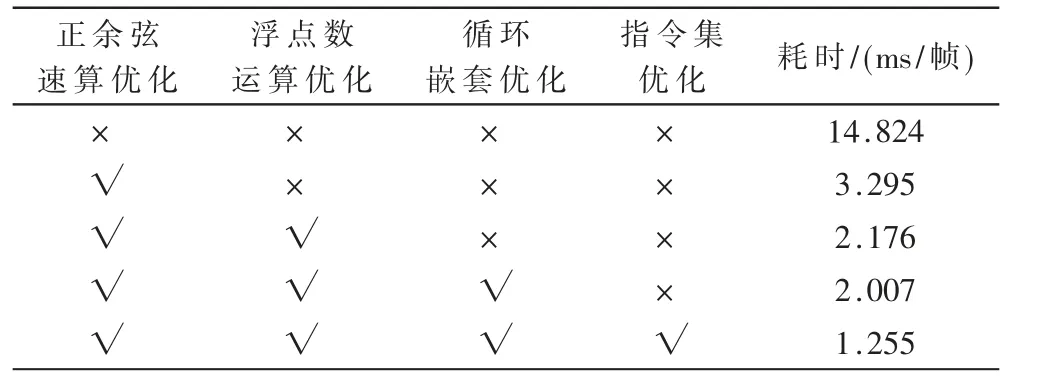
表1 优化结果显示
从实测结果上来看,使用三角函数速算算法设计的硬件电路对程序执行效率提高最明显,循环嵌套优化由于循环使用次数的原因,并未对程序处理提高太多效率。指令集的优化是建立在汇编语言的基础上,在满足处理实时性的前提下,可以适当使用指令集优化。 波束指向算法在卫星导航的平台上应用时,惯导周期在10 ms 到150 ms 之间,由INS 性能和指向类型决定。 在PowerPC的环境下,使用以上四种优化,已经满足绝大多数类型的波束指向的实时性的要求。
6 结论
本文在PowerPC 架构下提出了一种针对波束指向算法的优化策略,将算法处理的时间减少到1/10 左右,一方面,将CORDIC 旋转算法应用在波束指向算法中,在数学函数层面对系统实时性上提供了优化的空间,另一方面,PowerPC 本身的架构为波束指向算法的优化提供了可能性。 同时为PowerPC 平台的应用提供了一个很好的优化思路,指令集上的优化策略同样适用于所有基于PowerPC 平台的应用开发。 此外,基于CORDIC 算法的设计的硬件电路在芯片开发领域有很强的使用价值,打破了将复杂数学函数计算的负担交给纯软件来实现的传统。本论文提出的所有优化策略对其他平台的算法开发和算法优化也有一定的借鉴价值。

