一种基于噪声点邻域的形态学滤波算法研究*
文福林 ,张 凯 ,蒲 锋 ,汤素丽
(1.四川航天职业技术学院 电子系,四川 广汉618300;2.四川大学 机械工程学院,四川 成都610065)
0 引言
椒盐噪声是图像在成像、信道传输、解码等处理过程中产生的黑白相间的亮点或暗点噪声,也称为双极脉冲噪声[1]。 针对椒盐噪声的滤波方法有很多,如:标准中值滤波算法、自适应中值滤波算法、形态学滤波算法以及一些改进的滤波算法等[1-4]。
标准中值滤波算法的思想就是选取一定大小的滤波窗口,比较该滤波窗口内的像素值的大小,取其中值作为这个滤波窗口的中心像素新的值。标准中值滤波器受滤波窗口大小的影响较大,如果窗口较小,则能较好地保护图像中的一些细节特征,但滤效果就会变差;反之,如果窗口尺寸较大则有较好的滤波效果,但会丢失更多的图像细节特征。 且随噪声密度地增大,其滤波性能下降较为明显。
自适应中值滤波算法是基于对标准中值滤波算法的改进,引入了噪声判断机制,动态调整滤波窗口尺寸大小来改进滤波性能,相比标准中值滤波算法,其滤波性能有了较大程度的提高,可获得较好的滤波效果。 标准中值滤波算法以及自适应中值滤波算法因其使用滤波窗口的中值来代替中心像素的值,而滤波窗口的中值与中心像素值并不一定相等,从而引入额外的误差。
形态学广泛应用于图像边缘检测、抑制噪声、纹理分析、特征提取等[2-12]。 形态学开运算具有可去除比结构元素小的亮细节特性,而形态学闭运算具有可去除比结构元素小的暗细节特性[4],利用形态学开运算和形态学闭运算可以构成多种滤波器,如常见的形态学开闭组合滤波算法[4,10]以及形态学同其他滤波算法相结合等[2]。该类算法对噪声图像实施先开后闭运算,或者先闭后开运算,或者以先开后闭运算与先闭后开运算的均值来求解[10]。 然而,形态学开闭组合滤波算法受结构元素的影响较为敏感,当选取不同的结构元素时,其滤波效果会存在较大的差异。
为此,本文借鉴噪声判断机制,先判断出噪声图像中存在的可疑噪声点。对于一幅归一化的8 位灰度图像而言,灰度值为0 或灰度值为1 的点既有可能为噪声点,也有可能为非噪声点,即信号点[1,13]。 在此,将灰度值为0 的点定义为可疑椒噪声点,将灰度值为1 的点定义为可疑盐噪声点。 以可疑噪声点为中心,构建一个7×7大小的邻域,对可疑椒噪声点邻域进行形态学闭滤波,对可疑盐噪声点邻域进行形态学开滤波,并以滤波后的该邻域中心点的灰度值替换可疑噪声点的灰度值。对于非可疑噪声点,保留其灰度值不变。实验表明,该方案切实可行,滤波后的图像具有均方误差小以及峰值信噪比高等优点。 其滤波性能相比标准中值滤波算法、形态学开闭组合滤波算法、自适应中值滤波算法等均有一定程度的提高。
1 灰度图像形态学基本算法
灰度图像形态学算法是由二值形态学扩展而来的。其基本算法有膨胀、腐蚀、开运算和闭运算。 设f(x,y)为输入图像,b(x,y)为结构元素。
1.1 膨胀运算
用b 对f 进行灰度膨胀定义为:
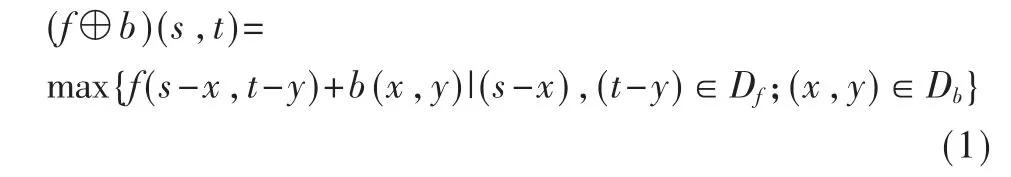
式中:⊕表示膨胀运算符号,Df和Db分别是f 和b 的定义域,平移参数(s-x)和(t-y)必须在f 的定义域内,而且x 和y 必须在b 的定义域内。 膨胀运算可使目标扩张,孔洞收缩,该运算是在由结构元素确定的邻域中选取f+b 的最大值,如果结构元素的值为正,则输出图像表现为暗细节被削弱或去除,亮细节得到增强。
1.2 腐蚀运算
用b 对f 进行灰度膨胀定义为:

式中:Θ 表示腐蚀运算符号。腐蚀可使目标收缩,孔洞扩张,该运算是在由结构元素确定的邻域中选取f-b 的最小值,如果结构元素的值为正,则输出图像表现为亮细节被削弱或去除,暗细节得到增强。
1.3 开运算
结构元素b 对f 进行开运算定义为:

式中,○表示开运算符号。 开运算相当于先用b 对f 腐蚀,腐蚀的结果由b 膨胀。 开运算可用来去除比结构元素更小的亮细节。
1.4 闭运算
结构元素b 对f 进行闭运算定义为:

式中:·表示闭运算符号。 闭运算相当于先用b 对f 膨胀,膨胀的结果由b 腐蚀。 闭运算可用来去除比结构元素更小的暗细节。
1.5 形态学开闭组合运算
由于形态学开运算具有可去除比结构元素小的亮细节的特性,而形态学闭运算具有可去除比结构元素小的暗细节的特性,因此它们经常被组合在一起用来平滑图像并滤除噪声。 常见的有两种类型,即形态学开闭组合滤波算法(Open-Close Filter,OCF)以及形态学闭开组合滤波算法(Close-Open Filter,COF)[10]。

1.6 结构元素的选取
形态学滤波的效果不仅仅与算法有关,还与结构元素的形状、尺度、滤波的次数等因素有关。选用大的结构元素可以较好地滤除噪声,但会丢失更多的图像细节特征; 选用小的结构元素可较好地保护图像的细节特征,但滤波性能又不足;滤波的次数越多,丢失的细节特征越多[14]。 为了兼顾去噪作用和保护细节的效果,本文选取半径为1 的圆盘型结构元素b1和边长为2 的方形结构元素b2。
2 本文改进算法原理
对于噪声图像g,按像素坐标依次判断各点是否为可疑盐噪声点,如果不是,则进入下一个点的判断;如果是,则以该可疑盐噪声点的坐标位置为中心,构建一个7×7 大小的邻域g11,g12,…,g1n,其中n 为可疑噪声点个数,超出图像边界的部分补值0.5,如图1 所示。

图1 一个7×7 含可疑盐噪声点领域内像素点的灰度值
对 含 有 可疑 盐 噪 声 点 邻 域g11,g12, …,g1n采 用 式(7)运算。

采用式(7)对图1 所示的领域滤波,运算结果如图2所示。
然后用滤波后的该邻域的中心点的灰度值替换可疑噪声点的灰度值,其他非可疑噪声点的灰度值保持不变。 即用图2 中心点的灰度值替换图1 中心点的灰度值,图1 中其余像素点的灰度值保持不变,如图3 所示。

图2 滤波后7×7 领域内像素点的灰度值

图3 替换可疑噪声点后7×7 领域内像素点的灰度值
同理,采用相同的方法构建可疑椒噪声点邻域g21,g22,…,g2n,其中n 为可疑噪声点个数,并采用式(8)运算。
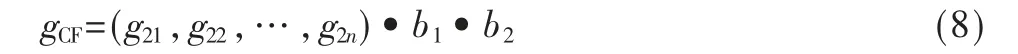
最后,即可得到无噪声的图像。
3 算法流程
本文主要算法流程如下:
(1)按像素坐标依次搜索噪声图像f 中存在的可疑噪声点,并判断该可疑噪声点属于盐噪声还是椒噪声。
(2)如果是可疑盐噪声点,则以该噪声点为中心,构建一个7×7 大小的邻域,超出图像边界的部分补值0.5,并对该邻域执行式(7)运算,再用滤波后的该邻域的中心点的灰度值替换噪声点的灰度值,其他非噪声点的灰度值保持不变。
(3)如果是可疑椒噪声点,则以该噪声点为中心,构建一个7×7 大小的邻域,超出图像边界的部分补值0.5,并对该邻域执行式(8)运算,再用滤波后的该邻域的中心点的灰度值替换噪声点的灰度值, 其他非噪声点的灰度值保持不变。
(4)最后可得无噪声的图像。
4 实验分析
本文采用256×256 大小的lena 图像进行仿真实验,对其添加椒盐噪声,其噪声密度d=0.2,如图4(a)所示。并采用图像的均方误差(Mean Square Error,MSE)及峰值信噪比(Peak Signal to Noise Ratio,PSNR)客观评价滤波效果。 假设图像大小为M×N,图像的MSE 及PSNR 定 义 为[5,15]:

采用标准中值滤波算法、自适应中值滤波算法、OCF算法、COF 算法以及本文算法对其滤波, 其滤波后的图像分别如图4(b)~图4(f)所示。

图4 滤波效果
仔细对比滤波后的图像可以发现,标准中值滤波算法、自适应中值滤波算法、OCF 算法、COF 算法以及本文算法虽然都具有一定的去噪能力,但自适应中值滤波算法以及本文算法滤波后的图像细节特征保存较为完好,尤其是本文算法不仅具有比较强的去噪性能,且能够更好地保留图像的细节特征。
为了客观地评价各算法滤波后的性能,表1 详细列出了不同噪声密度(d)条件下各算法的MSE 及PSNR 的值。

表1 各算法的均方误差及峰值信噪比值
通过对表1 中的数据对比可知,在同等噪声密度情况下,本文算法其MSE 值最小、PSNR 值最大,自适应中值滤波算法次之,标准中值滤波算法、OCF 算法及COF算法性能基本相近。 总体而言,本文算法具有均方误差小以及峰值信噪比高的优点,其滤波性能相比标准中值滤波算法、自适应中值滤波算法、OCF 算法、COF 算法等有一定程度的提高。
5 结论
本文经实验证明,对受椒盐噪声污染的图像,以可疑噪声点为中心,构建一个7×7 大小的邻域,对可疑椒噪声点邻域进行形态学闭滤波,对可疑盐噪声点邻域进行形态学开滤波,并以滤波后的该邻域中心点的灰度值替换可疑噪声点的灰度值,而非可疑噪声点的灰度值保持不变的方案切实可行。 但对于更高噪声密度的情况,如何能更好地滤除噪声,同时具备较强的细节保护能力是以后的重点研究方向。

