基于三种分析方法的PID控制规律的讲授

王玲玲， 雷军委， 梁 勇

(海军航空大学 岸防兵学院，山东 烟台 264000)

0 引言

PID控制是控制系统中非常重要的一种控制器。在控制理论相关课程的教学中，对于PID控制所占用的篇幅比重是比较高的。一般PID控制的教学会延续表1所示的思路。

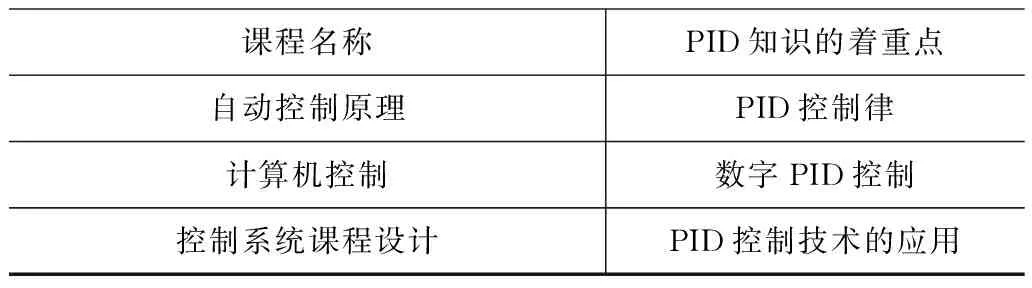
表1 PID控制的教学内容在培养方案中的体现

在“自动控制原理”课程中主要阐述的是PID控制的基本原理及其对系统性能的影响；在“计算机控制”课程中主要学习的是PID如何应用在数字系统中；在其后的“控制系统课程设计”中，则主要讲授的是实际PID应用的要点以及PID参数如何整定，此时学生需要将所学的PID的相关知识真正应用在一个具体的被控对象上。通过这一系列的学习安排，希望能够让学员对于PID的认识形成从理论到实践的一个完整的知识回路[1～2]。但是从实际的教学效果来看，情况却并不尽如人意。表现在学生始终对于PID参数如何能够影响系统性能，并没有非常深刻地理解，究其原因有两个方面。

首先就是在一开始学习PID控制律时，就没有形成一个深刻的印象。很多对于PID控制的教学一上来普遍采用的都是案例+仿真的模式，这种授课模式确实最为直观，但是对于这三种参数为什么能影响控制效果的深层次原因阐述得不够深刻，造成学生学习时也只是停在表相，和前面的知识也无法形成联系[3～4]。

此外，除了控制专业的学生，其他大多数专业实际上并不会学习“计算机控制”与“控制系统课程设计”，如此，在“自动控制原理”里没有吃透PID控制律，后续又不会有新的课程学习，那么就会对控制理论中非常重要的PID控制器无法进行深入地理解和运用，最终使“自动控制原理”这门课程的工程性和实用性大打折扣[5]。

因此本文从“自动控制原理”的PID控制律的教学入手，阐述一种教学设计，使得学员通过控制律的学习，能够将本门课所有的知识贯通下来，并对PID三个参数如何影响系统性能形成深刻地理解。

1 授课思路

在“自动控制原理”课程里，PID控制律是第六章中的内容。之前除了在第三章二阶系统的性能改善里提到过比例微分控制，这是控制理论课程中第一次真正接触到PID控制的知识，因此对于学生来说基本是一个新的知识点。因此我们的授课思路按照什么是PID？(PID参数的含义及框图)→为什么要学习PID？(PID控制器的应用)→PID有什么作用？(PID各部分的控制规律)来依次展开，这一授课思路如图1所示。

2 案例代入

PID控制是工程应用相当广泛的一种控制算法，对于其学习不可避免自然是要联系到工程实际。而且“自动控制原理”的授课内容其最大问题是抽象，学员通常难以建立理论与应用之间的联系，因此实际上在课堂授课时，都应尽可能地选取合适的工程实例，带着问题带着实例进行知识点的讲解。这样学生在学完一次课后，不仅能增强学员对控制系统的直观理解，培养其解决实际问题的能力，更能使学生切身感受到这门课程的工程性以及学习这门课程的实用性。

因此在一开始讲授时，可以以某一工程背景来引入，即为了达到一定的控制效果，实际中经常采用的控制算法是PID算法，之后引入本次课的主体内容；在PID控制器的应用中，将这个引例进一步展开，去阐述为什么要学习PID；最后在第三部分内容中，通过引例中的具体被控对象，去分析PID各部分的控制规律对系统的输出量究竟有何影响。

这里在案例中，我们选用的引例是导弹的某一次攻击任务，之后以三代PID控制(继电式、模拟式、数字式)在导弹中的应用来阐述其应用之广泛，最后分析PID各个部分在导弹俯仰通道中对俯仰角的影响，如图1所示。

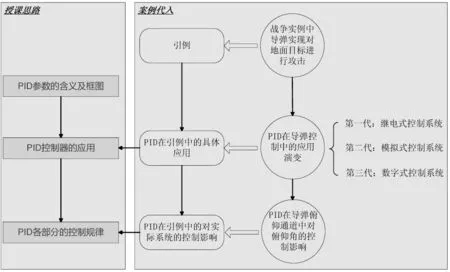
图1 总体授课思路

3 巧妙运用三种分析方法进行讲解

PID控制规律是在整门课程的第六章里，此时学生已经学完控制理论里的三种分析方法，分别是时域分析法、根轨迹法和频域分析法。但是此时，学生往往只是会定量的计算指标或者作图，对于如何应用这三种分析方法去分析系统，实际上并没有太多的综合运用的能力。另一方面，对于PID控制规律究竟如何影响控制系统性能的原因，如果只是单单从控制仿真曲线上阐明，很直观却不够深刻。因此本文将这二者结合，并使用具体的被控对象，如图2所示，通过三种分析方法的运用去深入剖析其控制规律，如图3所示。

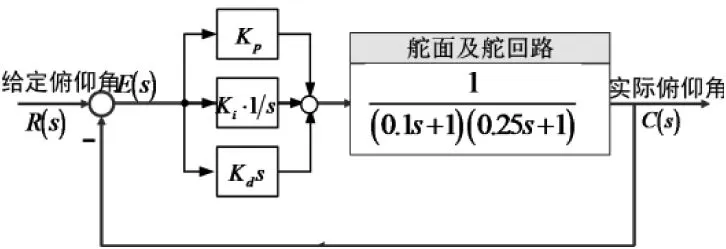
图2 PID控制讲解时用到的案例

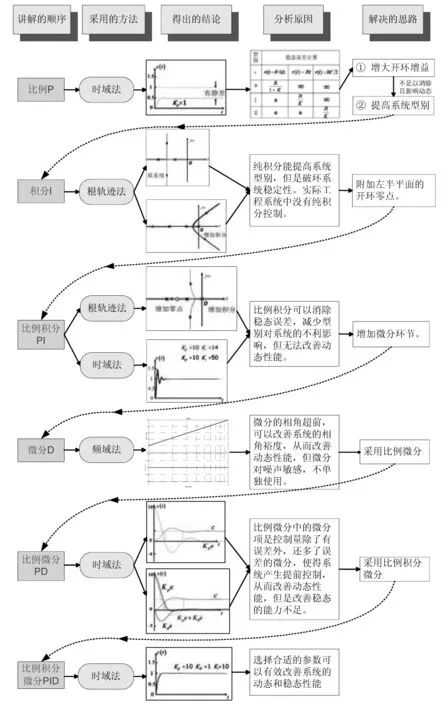
图3 综合运用三种分析方法

3.1 比例P

在PID控制器中首先只取比例控制，并用时域法分析具体案例。通过响应曲线得出此时性能指标的不足，如图3“比例P”这一行所示。可以分析出此时稳态性能较差，于是通过静态误差系数中 的3×3的表格分析原因，得出I型系统在输入为阶跃信号时稳态误差为

知道了稳态误差产生的原因，就可以考虑通过增大开环增益K来减小稳态误差，但继续仿真发现这种方式只能适当地减小误差却不能最终消除误差，而且增益过大会使得动态性能变差。因此考虑通过提高系统型别的方式来消除稳态误差，而提高系统型别即是在系统中加入积分环节，由此引出下面的积分控制。

3.2 积分I

单纯的纯积分环节串联在前向通路中是否能够可行呢？此时可以采用根轨迹分析方法，对原系统绘制根轨迹，会发现根轨迹都在左半平面，如图3“积分I”这一行所示，因此原系统是全稳定系统。而增加了纯积分环节后，相当于在原点处增加了一个开环极点，对于原根轨迹具有“排斥”作用，会将根轨迹“推到”右半平面，使得系统呈现条件稳定的状态，即纯积分环节会将本身全稳定的系统变成条件稳定系统，从而破坏了系统的稳定性。稳定性是控制系统的基本要求，破坏系统稳定性在实际系统中是不被允许的，因此实际工程系统中并没有纯积分控制。

那么如何既通过纯积分提高型别，又不会破坏系统稳定性呢？此时引导学生考虑“开环附加零极点对系统根轨迹的影响”这一知识点，通过再次增加位于左半平面的零点将根轨迹“吸回”左半平面。如此，既增加位于原点的极点，又增加位于左半平面的零点，其实，这就是下面所说的比例积分控制。

3.3 比例积分PI控制

在增加了纯积分的根轨迹图上，继续绘制增加左半平面开环零点的根轨迹，会发现只要开环零点选择合适，则系统的稳定性得以保证。此时继续使用时域法仿真分析，发现PI控制可以有效消除稳态误差，但是对动态性能的改善不足。因此考虑增加微分D控制。

3.4 微分D

微分为何能够起到改善动态性能的作用呢？可以引导学生使用频率法，即绘制微分环节的Bode图，如图3“微分D”这一行所示，会发现其相角是大于零的。一个相角超前的环节串联接在系统中，在合适的参数设置下会帮助系统提高其相角裕度，从而改善动态性能。但是微分环节对高频噪声具有放大作用，因此实际的工程系统中也没有纯微分控制，而是和比例合在一起形成比例微分PD控制。

3.5 比例微分PD

比例微分控制又是如何改善系统的动态性能的呢？此时分析的角度可以从时域法，也可以从频域法。但是通常频域法较为抽象，不如时域法直观，而且从实际课堂授课来看，还是采用时域法进行分析效果更好。

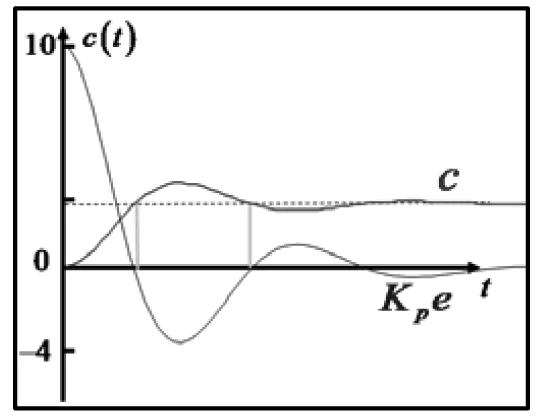
使用时域法来分析，首先分析不加微分只有比例控制的系统，此时被控对象的控制量就是偏差量乘以比例系数，即被控对象的输出c(t)在控制量Kpe(t)的作用下不断振荡逼近稳态值。每当控制量Kpe(t)为零时，输出c(t)都回到稳态值，但是由于惯性的作用，c(t)会继续偏离稳态值直至峰值停下，因此仅有比例控制的系统其输出c(t)要振荡多次才能最终在稳态值上恒定下来，如图4(a)所示。

(a)纯比例控制

而对于比例微分PD控制，此时被控对象的控制量除了有误差的比例信号Kpe(t)外，还有误差的导数信号Kde(t)，二者的叠加即为控制量的曲线，如图4(b)所示。由于误差信号e(t)是不断振荡减小的过程，因此对其微分的e(t)曲线必然要更负，从而Kpe(t)+Kde(t)的曲线比单纯的Kpe(t)曲线要靠下。从响应图4(b)中可以看出，每当输出c(t)还没有真正回到稳态值时，控制量信号在某一时刻就已经为零了，相当于在每次到达稳态之前，就已经提前踩了一脚刹车，而从控制量信号为零的时刻之后，至峰值时刻，是惯性的作用产生的，因此系统的输出不会偏离稳态值太远，而且整个调节过程也很快就能结束。

由此可以得到比例微分控制改善系统动态性能的根本原因是误差的微分作用使得系统有提前控制的效果。

3.6 比例积分微分PID控制

通过前述分析，PI可以改善稳态性能，PD可以改善动态性能，则二者结合，既可以改善稳态性能，也可以改善动态性能。最后通过时域分析得知，只要选择合适的参数就可以有效改善系统的动态和稳态性能，获得满足系统指标的响应曲线，如图3“比例积分微分PID”这一行所示。而如何选择参数，则是后续课程中需要介绍的知识点。

至此，通过不断的发现问题解决问题，并综合运用三种分析方法，时域法、根轨迹法、频域法，对PID控制中各项参数对系统性能的影响做了深入地讨论，同时还综合运用了课程的相关内容。

4 与后续课程的联系

在讲完PID控制规律后，后续就是讲解串联校正中的串联超前校正、串联滞后校正以及串联超前滞后校正。很多时候学生都是认为这两大部分内容是完全脱节的，实际上还是没有明白这其中的联系。因此在PID控制规律内容之后，或者串联校正内容之前，通过引入的方式，阐述这两大块内容的联系。

其中，PI控制器传递函数可写为

绘制伯德图如图5(a)所示，可以看出其相角小于零，所以PI控制就是一种滞后校正。

同理，PD控制器传递函数可写为

绘制伯德图5(b)所示，可以看出相角大于零，所以PD控制就是一种超前校正。而PID控制二者皆有之，为一种滞后超前校正。

(a)比例积分控制器

5 结语

本文运用“自动控制原理”中三种分析方法，以发现问题解决问题的思路，通过具体案例讲解PID控制的基本含义、应用和控制规律。(王玲玲等文)

这部分的授课内容在多个班次进行实验，取得的效果非常好。本专业的学生对这一部分的内容学习起来更有连贯性，掌握得也更为透彻。而且该授课内容在校内经多位专家的指导点评，并多次获得系级、院级一等奖，具有一定的推广意义和参考价值。