能量守恒定律在Boost变换器分析中的应用

李湘峰， 屈莉莉， 庄梓丹， 张惠桃

(佛山科学技术学院 机电工程与自动化学院，广东 佛山 528000)

0 引言

随着社会经济的发展和科学技术的进步，电力电子技术在电动汽车、机器人以及智能电网等领域得到了越来越广泛的应用。虽然电力电子技术在我国的现代化建设中意义重大，但我国电力电子技术相关人才却一直较为缺乏，因此，通过高效的“电力电子技术”课程教学培养高素质的电力电子技术研发人员具有较大的现实意义。

电力电子技术涉及电力技术、电子技术、电磁技术以及控制技术等相关学科，知识结构复杂、所需知识点跨度较大而难以理解，对教师的授课技巧与学生对知识的接受能力提出了较为严峻的挑战。以Boost变换器为例，目前，“电力电子技术”教材[1，2]对于Boost变换器的分析方法较为统一，其分析过程中运用到的电学理论较多，主要包括伏秒平衡、电磁感应以及面积等效原理等。学生对部分理论知识点较为陌生，对相关公式的理解不够深刻、从而导致学习效果差强人意。实践证明，若能从学生较为熟悉的理论知识入手对Boost变换器进行分析，最终再与教材现有分析方法进行对比学习，即可取得较好的教学效果[3～5]。调查表明，电子电气类学生对于自然界的三大守恒定律，特别是能量守恒定律相对比较熟悉，且能量守恒定律在电力电子前沿技术研究方面也获得了较成功的应用[6]，基于此，本文拟采用学生较为熟悉的能量守恒定律作为理论工具，对Boost变换器的工作特性进行分析与计算，以期为“电力电子技术”课程的教学提供一种新的思路。

1 Boost变换器工作特性分析

图1所示Boost变换器广泛应用于新能源发电、电池管理系统以及功率因数校正等领域，属于电力电子学科三大基本DC/DC变换器拓扑之一。

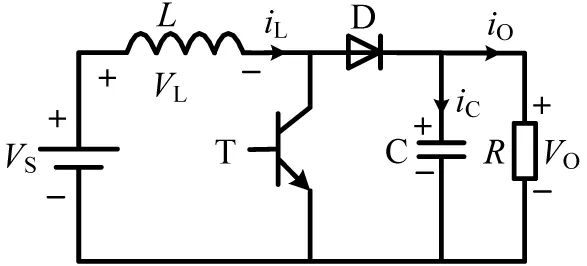
图1 Boost变换器电路结构

若不考虑Boost变换器的潜电路工作模式[7]，可认为该变换器存在两种基本工作模式，即电感电流连续模式CCM(Continuous Current Mode)和电感电流断流模式DCM(Discontinuous Current Mode)。电感电流连续模式，即电感电流在整个开关周期内均大于0而保持连续，该模式下Boost变换器电路存在两个电路状态，其等效电路如图2所示。

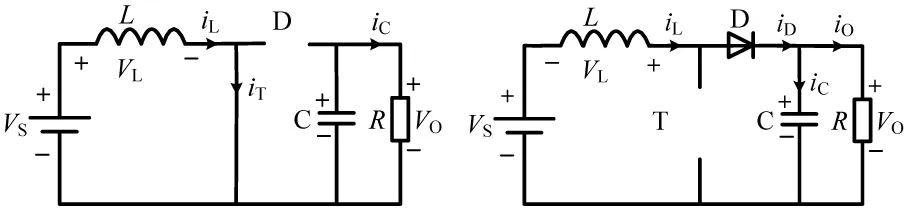
(a)电路状态1 (b)电路状态2图2 电感电流连续模式下Boost变换器等效电路

电感电流断续模式，即电感电流在某一时间段为0而断流，该模式下Boost变换器电路存在三个电路状态，相比电感电流连续模式其主要区别在于存在一个电感、开关管以及二极管均无电流流通的过渡状态，其等效电路如图3所示。

(a)电路状态1 (b)电路状态2

电感电流连续模式下Boost变换器典型电路波形如图4(a)所示。波形从上至下依次为开关管T门极驱动波形VG、电感L的电流波形iL、开关管T的电流波形iT、二极管D的电流波形iD以及电感L两端的电压波形VL。电感电流断续模式下，上述参量波形如图4(b)所示。

(a)电感电流连续 (b)电感电流断续图4 Boost变换器主要工作波形

2 Boost变换器增益函数的求解

2.1 电感电流连续模式

电感电流连续模式下Boost变换器等效电路及其工作波形如图2及图4(a)所示，该模式下Boost变换器拥有2种电路状态。

(1)电路状态1：开关管T导通、二极管D截止，此时Boost变换器等效电路如图2(a)所示。此状态下，电源电压VS作用于升压电感，使得电感电流iL线性增长。根据电磁感应定律，在此期间电感电压满足方程：

(1)

(2)开关状态2：开关管T截止、二极管D导通，此时Boost变换器等效电路如图2(b)所示。此状态下，电压源VS以及电感电流iL一起向负载及电容供电。假定输出电容足够大，即输出电压VO在一个开关周期TS中恒定不变，则在开关管T截止期间，电感电压满足方程：

(2)

电路达到稳态时，电感需满足伏秒平衡原则，即：

VL_Ton·Ton+VL_Toff·Toff=0

(3)

将式(1)、式(2)代入式(3)可得：

VS×Ton=(VO-VS)×(1-D)TS

(4)

其中D=Ton/TS为占空比，化简得：

(5)

式(5)即为电感电流连续模式下Boost变换器的增益函数，从式(5)可见，电感电流连续模式下，Boost变换器的电压增益仅与占空比有关。

2.2 电感电流断续模式

电感电流连续模式下Boost变换器等效电路及其工作波形如图3及图4(b)所示，该模式下Boost变换器拥有3种电路状态。

(1)电路状态1：开关管T导通、二极管D截止，其等效电路如图3(a)所示。该状态持续时间为Ton，该状态下电感两端电压被输入电源钳位至VS，其电压方程如式(1)所示。

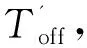
(6)

(3)开关状态3：开关管T与二极管D均截止，其等效电路如图3(c)所示。该状态持续时间为TO在此期间电感电流iL保持为0，电感两端电压也为0。在整个开关周期中，电感依旧遵守伏秒平衡原则，即有：

(7)

在开关状态3期间，电感电压为VL_TO=0，因此有：

(8)

化简后可得：

(9)

式中D1=Toff/TS。

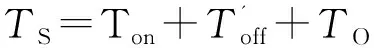
(10)

(11)

2LfSIOM2-2LfSIOM-VD2=0

(12)

运用求根公式求得电感电流断续模式下Boost变换器的电压增益为

(13)

由式(13)可见，电感电流断续模式下Boost变换器的电压增益不仅与占空比相关，还与输出电压、负载电流、开关频率以及电感值大小等有关。

3 变换器分析中能量守恒定律的运用

由前述分析过程可见，Boost变换器电压增益计算较为繁琐，计算过程中运用了伏秒平衡、电磁感应以及面积等效等理论知识，若对上述理论知识不熟悉或理解不够深刻，将对学习效率产生较大影响。因此，若从学生较为熟悉的能量守恒定律着手分析Boost变换器的电压增益将会取得较好的教学效果。

3.1 电感电流连续模式

(1)电路状态1：等效电路如图2(a)所示。此状态下，电源电压VS作用于升压电感并对其充电，使得电感电流iL线性增长。iL的增量△iL+可表示为：

(14)

(2)电路状态2：等效电路如图2(b)所示。此状态下，电压源VS以及电感电流iL一起向负载及电容供电。假定输出电容足够大，输出电压VO在一个开关周期TS内恒定不变，在此条件下，iL在Toff=TS-Ton时间内的减少量△iL-为：

(15)

根据能量守恒定律，电感增加(吸收)的能量与电感减少(释放)的能量必定相等，则有：

(16)

即

(17)

化简可得：

(18)

显然，式(18)所示结果与目前教材所得分析结论一致。

3.2 电感电流断续模式

(1)开关状态1：等效电路如图3(a)所示，此时电源VS对电感L充电，持续时间为DTS，此状态期间，电源提供的能量可表示为：

(19)

(2)开关状态2：等效电路如图3(b)所示，在此状态下，电源VS与电感L一起为输出电容与负载提供电能，持续时间为D1TS。电感电流iL的减少量△iL-为：

(20)

此状态结束时，在开关状态1中所储存的电能完全得以释放，由于电感充放电过程也遵循能量守恒定律，因此电路状态1中所充入的电能必定等于电路状态2期间所释放的电能，即有

(21)

将式(19)、式(20)代入式(21)得：

(22)

化简可得：

(23)

在开关状态2期间，电源 持续对负载提供能量，所提供的能量为电源输出电压乘以电源输出电流再乘以时间，即：

(24)

(2)开关状态3：等效电路如图3(c)所示，电感与电源停止对负载供能，负载由电容提供能量。

为便于分析，假设输出电容足够大且无功率损耗，输出电压在整个开关周期期间保持恒定，则负载在整个开关周期所消耗的电能为 ，根据能量守恒定律，负载所消耗的能量 必然等于电源所输入的总能量 ，即：

(25)

经整理可得：

(26)

其中，fS=1/TS为开关频率。将式(23)代入式(26)，并化简可得：

(27)

运用求根公式，求得VS：

(28)

用VO除以VS并进行整理即可得到电感电流断续模式下Boost变换器的增益函数：(李湘峰等文)

(29)

对比式(5)与式(18)以及式(13)与式(29)可知，根据能量守恒定律推导得出的Boost变换器电压增益与目前教材所推导的电压增益函数完全一致，从而印证了本文分析方法的正确性与可行性。

4 结语

合适的教学方法与分析思路往往能起到事半功倍的效果，为此，本文了提出了一种基于能量守恒定律的Boost变换器分析方法。教学实践表明，相比于目前教材所采用的方法，应用能量守恒定律对Boost变换器进行分析，其过程更为直观、易懂。应用本文所提出的分析方法与目前教材所采用方法进行对比验证，还可加深学生对Boost变换器工作原理、特性的理解，从而有效地降低了学习难度，提高了学习效率。该方法不仅适用于Boost变换器的分析与计算，也适用于其他类型DC/DC变换器的分析与研究。