汉江流域河网分级特征研究
黄子叶 王易初 倪晋仁
汉江流域河网分级特征研究
黄子叶 王易初 倪晋仁†
北京大学环境工程系, 水沙科学教育部重点实验室, 北京 100871; †通信作者, E-mail: jinrenni@pku.edu.cn
为深入了解汉江流域河网结构特征, 在提取高精度数字河网的基础上, 结合地表水频率地图和河宽遥感数据集, 研究河网几何结构和拓扑结构的自相似性, 同时统计分析河网的河宽分级规律。结果表明, 河网中 1~6 级的分支比、河长比、面积比和侧枝比等结构参数稳定在较窄的数值范围内, 证明 1~6 级河网具有良好的几何拓扑结构自相似性。在河网自相似级别范围内, 河流级别与河宽平均值呈现近似指数分布, 1~6 级的河宽比数值稳定, 平均值为 1.87, 说明 Horton 定律适用于河宽分级。通过对比沟河识别前后的河网参数发现, 河长、河宽和流域面积越小, 河流越容易“干涸”, 并导致低级别河流偏离河网结构的自相似性。
汉江流域; 河网; 河流级别; 河宽; 自相似性
河网结构直接影响流域径流、泥沙和溶质等物质的输移过程, 同时也是河流温室气体排放、生物多样性、河岸植被功能和食物网结构等诸多自然过程的主要控制因素[1-4]。河网的分支结构是一个重要的拓扑地貌特征, 几何和拓扑特性可以定量地描述河网中水文、地貌、生态和生物过程的联系, 有助于进行全面的数值模拟以及开发动态拓扑预测模型[5-10]。
河网的层次分枝结构可以通过河网分级法则来描述。河网分级是确定河流拓扑关系的重要手段, 最常用的方法是 Horton-Strahler 分级法, 由该方法划分的河流级别是 Horton 定律定量表述的基础[11-12]。Horton 定律表明, 河流的级别与河流数量、平均河长、平均流域面积和平均河道坡度之间存在几何关系, 还可以通过分支比、长度比、面积比和坡度比等霍顿比深入地刻画河网的几何结构。河网的几何结构自相似性体现为一个流域的霍顿比是不随河流级别变化的定值[13-16]。在 Horton-Strahler 分级体系的基础上, Tokunaga[17]引入表征河流入汇关系的侧枝比来展示河网拓扑结构的自相似性。
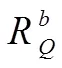
河流宽度的分级规律是水力几何变量 Horton定律中最重要的规律之一。河流宽度是控制河流水文、地貌、生态和生物地球化过程的最基本参数之一, 反映流经的水量、所携带的泥沙、河床和河岸的组成以及地形和构造的影响[23-24]。现有的关于河宽分级规律的研究主要依据有限的河宽实地测量数据或水力几何关系等经验公式, 缺乏高精度河网下真实河宽的分级规律研究。分辨率不断提高的地形和遥感影像数据有助于数字河网的提取以及河网结构和形态特征的量化, 逐渐发展出基于遥感影像由水体掩膜自动提取河宽的算法[25]以及全球高精度河宽遥感数据集 GRWL[26]。
本文基于 30m 精度的数字高程模型(DEMs)提取分级河网, 通过地表水高分辨率地图[27]进行沟、河识别, 结合全球河宽遥感数据集, 研究汉江流域的河网几何拓扑特征与结构自相似性以及分级河宽的统计规律。通过建立自相似河网中河宽的统计规律, 揭示地貌、水文和水力学特征在河网中的相互联系, 理解河网几何结构、统计特征和河流动力学特征在空间尺度上的相互耦合, 为河网中沉积物和污染物的分级输移研究提供理论基础。
1 资料与方法
1.1 研究区域
汉江是长江的一级支流, 发源于陕西省秦岭南麓, 干流流经陕西、湖北两省, 在武汉市汉口龙王庙汇入长江。干流全长 1577km, 以丹江口和钟祥为界分为上、中、下游, 其中上游长约 925km, 中游长约 270km, 下游长约 382km。汉江流域位于30°8′—34°11′N, 106°12′—114°14′E (图 1), 流域面积为 15.9 万 km2, 水系呈叶脉状, 支流众多。该流域的降水主要是降雨, 降雪和冰雹很少, 多年平均雨量约为 700~1100mm, 年内分配极不均匀, 年平均雨量的分布大致呈自西北向东南递增的趋势[28]。
1.2 河网提取与分级
基于 30m×30m 水平分辨率的 ASTER GDEM (http://www.gscloud.cn/), 本文以全球河宽数据集GRWL[26]中汉江流域的河宽中心线矢量数据为主(图 1), 结合流域水文数据集中的河流矢量数据[29], 对汉江高级别河段进行烧录, 运用 Bai 等[30]的高精度大规模河网提取程序来提取分级河网。该程序采用阈值过滤法识别河道, 选取临界集水面积和临界坡度作为阈值。若集水面积阈值设定得过小, 会出现伪河道, 反之则会遗漏一些低级别的河流。孔凡哲等[31]将河网密度随集水面积阈值变化趋于平缓的点对应的阈值作为最佳阈值, 李照会等[32]将河网密度-集水面积阈值曲线由骤减到缓慢减少的拐点作为最佳阈值。采用李照会等[32]的方法确定汉江的最佳集水面积阈值为 25 个栅格。此外, Bai 等[30]和Wang 等[33]在运用高精度河网提取程序时, 将临界坡度设为 0.01, 产生的河网可靠性更高, 同时避免大部分平行河网的产生。综合上述分析, 本文将集水面积 25 个栅格和临界坡度 0.01 作为高效河网提取算法河段识别的阈值。
采用 Horton-Strahler 分级法定义河流的级别[12],其中源头不分支的河流为一级河流。在汇流处, 下游河流的级别遵循以下规则:

图1 汉江流域概况

其中,d为下游河流的级别,1和2分别为汇合处上游河流的级别。
1.3 河网结构参数估算
河网几何结构特征通常用 Horton-Strahler 法则表达, 河网中河段数目、平均河长和平均流域面积与河段级别的关系均符合 Horton 定律。该定律提出分支比、河长比和流域面积比等河网几何结构自相似性参数。
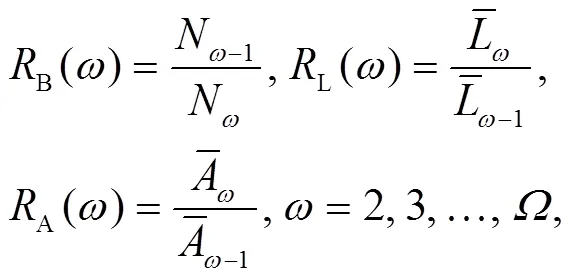

河网拓扑结构特征常用Tokunaga法则表征[17]。对于Horton-Strahler及别数为的河网, 汇入1级支流的1级支流数目为1,1, 汇入2级支流的1级支流数目为1,2, 汇入级支流的级支流数目为N,j(≤≤)。Tokunaga法则中定义侧枝比为

其中,N为级别为的所有河流数目。当T,i+k=T, 1≤≤时, 河网是拓扑自相似的, 其中T为平均侧枝比。
1.4 沟河识别
由于高效河网提取算法仅考虑地形, 不考虑下垫面、气候和人为因素的影响, 因此基于 DEMs 提取的河网不完全是真实的河流, 其中还包含无水的沟道, 需要通过沟、河识别, 进一步去除没有水的“伪河道”。Wang 等[33]在研究中国河流数目时, 提出两种沟河识别的方法。第一种方法认为干燥指数小于 0.2 时, 河道内基本上不存在径流; 第二种方法则依据 1984—2015 年 30m 水平分辨率的全球地表水出现频率数据 WO[27], 将 WO 值始终为零的河道识别为沟道。本文采用第二种方法。
1.5 河宽分级估算
GRWL 数据集为包含河宽测量值的河流中心线矢量数据集, 每 30m 为一个河段, 河宽中心线可以视为不完整的河网。本文运用 ArcGIS 中的空间连接工具, 将处于同一位置的河宽中心线与分级河网连接起来, 即分级河网中的一个河段对应若干河宽测量值。
由于河宽数据库几乎只包含 3 级以上的河流, 没有与分级河网中低级别河流对应的河宽测量值, 因此需要补齐低级别河段缺失的河宽值。Leopold 等[18]提出河流的宽度与流量之间存在一致的幂律关系:
=, (4)
其中,和为经验参数,≈0.5。流量数据一般通过河流监测站点获取。流量与流域面积之间存在如下关系:
=, (5)
其中,和为经验系数和指数,≈1.0。式(4)和(5)相当于建立了河宽与流域面积之间的幂律关系, 即可用上游流域面积直接估算缺失的河宽值。本文利用《中国 2017 年流域泥沙公报》中长江流域各个水文站点的多年平均流量及其对应的水文站点控制流域面积, 建立流量与流域面积之间的幂律关系, 然后通过水文站点的多年平均流量与站点河段的平均河宽测量值, 建立河宽与流量之间的幂律关系。最后, 基于分级河网中流域面积, 估算缺失的河宽值。
分级河网中每一个河段都有与之对应的河宽测量值或估算值, 将每个流域的河宽按照级别汇总, 得到河宽的分级分布。类似于分支比, 定义河宽比为高级别平均河宽与低级别平均河宽的比值:

2 结果与讨论
2.1 河网提取结果
图 2 展示汉江流域去除沟道之后的分级河网。根据 Horton-Strahler 分级法则, 将汉江流域河网分为 1~9 级, 其中 9 级为最高级别干流, 图 2 中仅包含4~9 级河流。汉江的分级河网中, 不仅包含河段级别信息, 还包含上下游拓扑关系、河段长度、流域面积和河道坡度等基本信息。
2.2 河网结构自相似性
2.2.1 几何结构自相似
图 3 给出汉江流域去除沟道前天然河网的分支比、面积比和河长与河流级别的关系。1~6 级河流的霍顿比稳定在较窄的数值范围内, 其中分支比平均值为 4.47, 面积比平均值为 4.52, 河长比平均值为 2.16, 与已有研究的参数取值[34-36]较为一致。当河流级别大于 6 时, 霍顿比值随着级别的变化出现较大波动, 逐渐偏离 1~6 级的平均值。这说明流域内低级别河流(1~6 级)更容易满足河网的几何结构自相似规律, 由于受到流域宏观地形条件的影响以及河流汇流能力的限制, 较高级别河流偏离自相似规律。
2.2.2 拓扑结构自相似
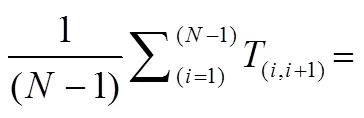
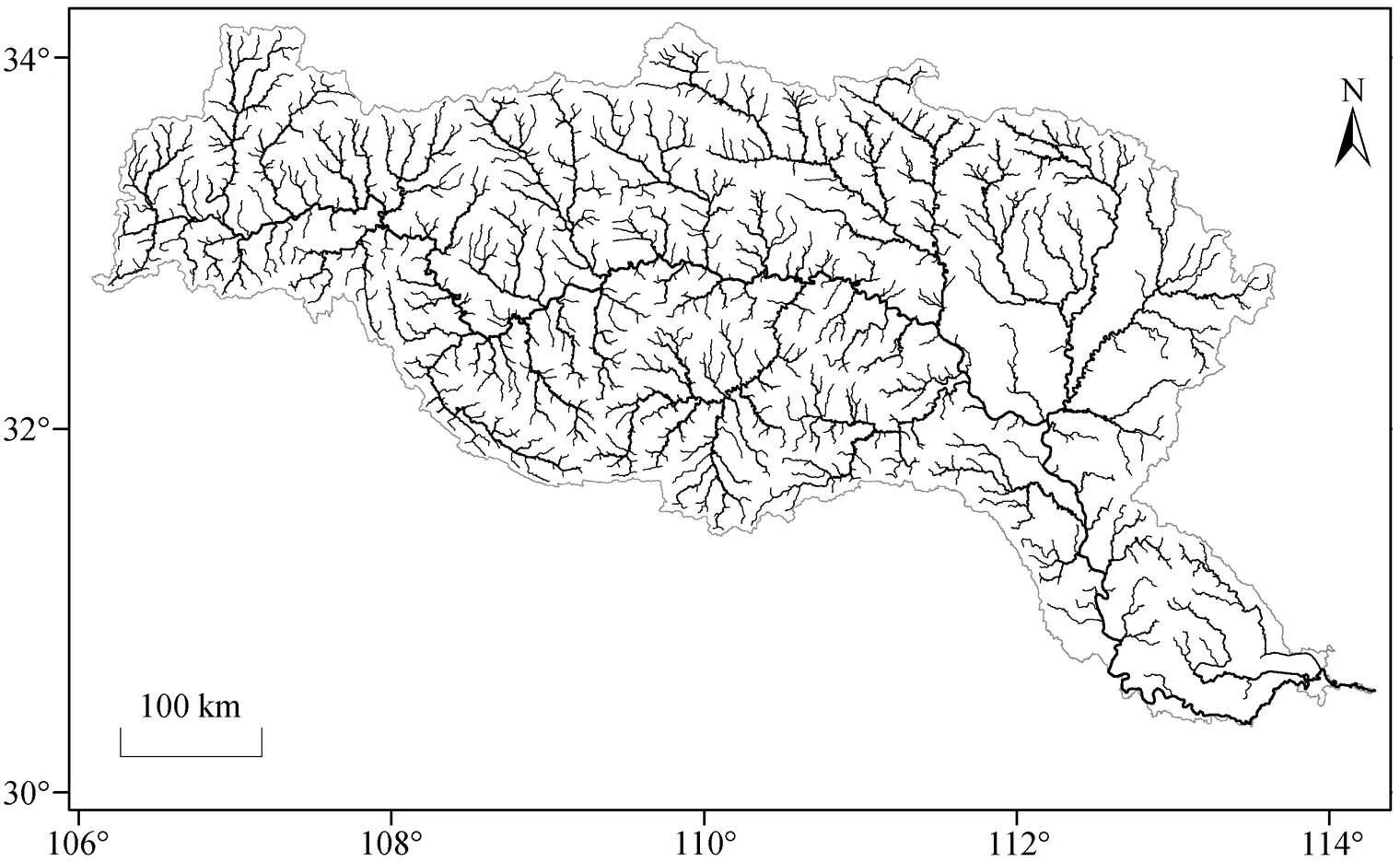
图2 汉江流域河网(4~9级河流)

图3 汉江流域不同级别的霍顿比

图4 汉江流域不同河流级别的侧枝比
2.3 沟河识别结果
汉江流域河网中去除的无水沟道包括地形上的沟壑以及干涸的沟道两种。通过对比去除沟道前后各级别河流的数目和特征, 可以看出真实河网与天然河网之间的差距。由图 5 可见, 无水沟道对应的是河网中 1~5 级河流。
由图 5(a)中去除沟道前后的河流数目可以看出, 河流级别越低, 河流数目减少得越多, 其中 1~5 级河流数目分别减少93%, 87%, 73%, 48%和 23%。1~9 级分支比变为 2.4, 2.3, 2.3, 2.9, 3.2, 3.9, 5.0和 3.0, 低级别分支比数值波动不大, 1~6 级分支比平均值为 2.62, 说明去除沟道后河流数目与级别之间的关系仍满足霍顿河数定律。由此可见, Horton定律的线性规律反映了绝大多数天然河网的“最可能的状态”, 而真实的河网可能因降雨等气候因素、植被等下垫面因素以及引水等人为因素的影响, 不如天然河网密集。越靠近源头的级别越低的支流, 越有可能在沟河识别的过程中被去除, 说明在较为干燥的区域, 源头低级别河流比高级别干流更容易“干涸”和“消失”。
由图 5(b)中去除沟道前后的平均河长可以看出, 1~5 级的平均河长分别增加 56%, 78%, 50%, 26%和14%。一般情况下, 河流级别越低, 平均河长增大的幅度越大。由图 5(c)中去除沟道前后的平均流域面积可以看出, 1~5 级的平均流域面积分别增加 139%, 103%, 55%, 26%和 12%, 河流级别越低, 平均流域面积增加的幅度越大。由此可见, 某一级别去除的沟道是该级别所有河道中长度较短且流域面积较小的那一部分, 真实河流则是河长较长且流域面积较大的那一部分。另一方面, 去除沟道后, 1~9 级河长比变为1.8, 2.0, 1.9, 2.2、1.9, 1.0, 3.3和2.1, 1~9 级面积比变为 4.0, 3.5, 3.6, 4.1, 3.8, 3.8, 6.7和 3.8, 可以看出1~6 级河长比和面积比数值波动不大, 1~6 级河长比和面积比平均值分别为 1.96 和3.80, 说明去除沟道后的真实河网仍然满足河长定律和面积定律。

图5 汉江流域去除沟道前后不同级别的结构参数
2.4 河宽分级规律
在排除位于湖泊水库、潮汐河口以及运河的河宽中心线后, GRWL 河宽数据集仅包含河宽测量值大于等于 30m 的河段, 即河宽较大的较高级别河段。河宽中心线与分级河网空间连接后的分析结果表明, 汉江流域河宽测量值对应的河流级别为 4~9级。对于缺乏河宽测量值的低级别(1~3 级)河段, 可以运用河宽与流量、流域面积的经验公式估算河宽缺失值。汉江流域流量与流域面积的幂函数关系为=0.11320.8491, 河宽与流量的幂函数关系为= 7.36830.5052。
图 6 展示去除沟道前后不同级别河宽的分布情况。随着河流级别增大, 河宽的下限值、下四分位数、平均值、中位数、上四分位数和上限值总体上都增大。各级别河宽中位数位于上下四分位数的中心位置, 分布偏态性不强。下文中, 河宽均指去除沟道后的河宽。
去除沟道后, 汉江流域 1~5 级河流平均河宽分别增大 31%, 28%, 19%, 12%和 5%, 说明某一级别去除的沟道是该级别所有河道中较窄的河流, 真实河流则是较宽的河流。另外, 去除沟道前后的 1~6级河宽比平均值分别为 1.97 和 1.87, 变化不大。
综上所述, 本研究在河网结构自相似的级别范围内, 基于高精度河网和河宽遥感数据, 验证了河宽的 Horton 定律。
2.5 DEM分辨率的影响
为研究 DEM 空间分辨率对河网结构的影响, 下面分析 30m 水平分辨率的 ASTER GDEM 和 90 m水平分辨率的 SRTM DEM 对应的流域河网分级特征的不同之处。研究表明, DEM 的分辨率会影响集水面积阈值的选取, 随着 DEM 栅格尺寸的增大, 集水面积阈值也随之增大[38-39]。基于 30m 水平分辨率的ASTER GDEM 提取河网时, 选取的集水面积阈值为 25 个栅格(即 0.0225km2); 基于 90m 水平分辨率的 SRTM DEM 提取河网时, 运用相同的方法获得集水面积阈值为 6 个栅格(0.0486 km2)。

图6 汉江流域不同级别的河宽
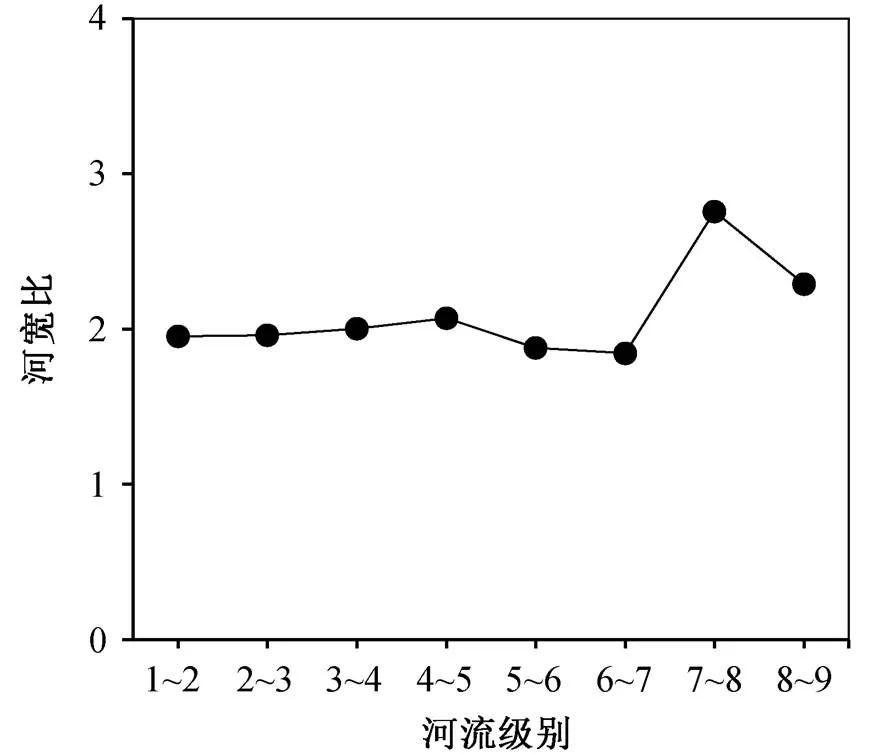
图7 汉江流域不同级别的河宽比
随着 DEM 分辨率和集水面积阈值的改变, 河网的汇流过程和分级结果也会发生变化。如图 8 所示, 基于两种分辨率 DEM 提取的汉江河网, 最高河流级别都是 9 级, 但两种分辨率 DEM 提取河网对应的结构参数不同。若无特别说明, 下文中结构参数均指去除沟道前的数值。由图 8(a)可以看出, 90m精度河网中, 各级河流数目均小于 30m 精度河网(9级除外), 1~8 级河流数目比 30m 精度河网减少27%~40%。由图 8(b)可以看出, 90m 精度河网中 1~ 7 级平均河长大于 30m 精度河网, 90m 精度河网总河长为 182348km, 30m 精度河网总河长为 197432km, 随着 DEM 精度的降低, 河网总河长(河网密度)减少 7.64%, 去除沟道后河网密度也减少, 说明 90 m 精度河网未识别出部分低级别源头河流。由图8(c)可以看出, 90m 精度河网中 1~8 级平均流域面积大于 30m 精度河网。总体来看, 随着 DEM 精度的降低, 集水面积阈值增大, 各级别子流域平均河长和平均流域面积增大, 河网密度减小。同时, 90m精度河网中, 在 1~6 级范围内霍顿比值仍稳定在较窄的数值范围内, 其中 1~6 级分支比平均值为 4.64, 面积比平均值为 4.75, 河长比平均值为 2.22, 90m精度河网在 1~6 级范围内仍然满足结构自相似性。
在河网结构随 DEM 分辨率改变的同时, 河宽的分级分布规律也随之变化。由图 9 可以看出, 两种 DEM 提取的河网去除沟道后的各级别河宽分布有一定的差距。除最高级别外, 90m 精度河网中各级别的河宽特征值(上下四分位数、中位数和平均值)一般大于 30m 精度河网。随着 DEM 栅格尺寸的增大, 1~8 级河宽中位数平均增大 23%, 1~8 级河宽平均值平均增大 31%, 与各级别河流平均流域面积增大的结果一致。90m 精度河网中, 4 级以上河宽分布偏态性较强, 只在 1~4 级范围内河宽平均值与河流级别存在较强的指数关系, 河宽的自相似性不明显。

图8 汉江流域两种分辨率DEM对应的河网结构参数
上述结果表明, 如果采用 90m 水平分辨率的SRTM DEM, 会遗漏一些低级别的河流, 使得河网密度降低, 各级别河流的河长、流域面积和河宽平均值大于 30m 精度的河网, 同时河宽的自相似规律变得不明显。高精度 DEM 则不会遗漏低级别河流, 因此基于 30m 水平分辨率的 ASTER GDEM 得到的结果准确度较高。
2.6 不确定性分析
本文研究结果的不确定性主要来自两方面。
1)河宽数据集和地表水出现频率数据集存在误差。GRWL 河宽数据集是多年平均流量对应的遥感影像衍化的平均数值, GRWL 河宽与实地测量河宽之间的均方根误差为 25.2 m, 两者之间的回归拟合优度为 0.81。地表水出现频率(WO)是 1984—2015年期间河道出现径流的百分比, 其正确率为 97.8%~ 99.7%。
2)沟河识别阈值的选取会带来不确定性。本文将 1984—2015 年期间地表水出现频率始终为零(WO=0)的河道识别为沟道, 该阈值是比较严格的沟河识别标准。对比沟河识别前后的结果可以看出, 河网结构自相似和河宽自相似的级别范围是不变的(1~6 级), 去除沟道前后河宽比变化为 8.1%, 说明沟河识别带来的不确定性较小。
此外, 文中建立的河宽、流量和流域面积三者之间的幂函数关系也会带来一定的不确定性。流量和流域面积的拟合优度为 0.97, 河宽测量值和流量的拟合优度为 0.86。
3 结论与启示
本文通过对汉江流域分支比、河长比、面积比和侧枝比等河网结构参数的分析, 发现低级别范围内(1~6 级)河网具有良好的几何拓扑结构自相似性。汉江流域河网不仅数目、长度和流域面积满足自相似性, 河流宽度也近似地满足自相似性。河宽分级统计结果表明, 可用 Horton 定律近似地描述河宽, 1~6 级河网的河宽具有较好的自相似性。将河网结构自相似推广到河宽等水力学几何变量的分级统计中, 有利于揭示河网几何结构与河流水力几何学的联系。河网中河数、河长、流域面积和河宽等分级特征可为流域水资源的合理分布提供有效的空间模板, 并为流域水资源管理提供科学依据。

图9 汉江流域两种分辨率DEM对应的河宽分布
[1] Widder S, Besemer K, Singer G A, et al. Fluvial network organization imprints on microbial co-occurrence networks. Proceedings of the National Academy of Sciences, 2014, 111(35): 12799–12804
[2] Sklar L S, Dietrich W E, Foufoula-Georgiou E, et al. Do gravel bed river size distributions record channel network structure?. Water Resources Research, 2006, 42(6): 770–775
[3] Hotchkiss E R, Hall Jr R O, Sponseller R A, et al. Sources of and processes controlling CO2emissions change with the size of streams and rivers. Nature Geoscience, 2015, 8(9): 696–699
[4] Hette-Tronquart N, Belliard J, Tales E, et al. Stable isotopes reveal food web modifications along the upstream-downstream gradient of a temperate stream. Aquatic Sciences, 2016, 78(2): 255–265
[5] Czuba J A, Foufoula-Georgiou E. Dynamic connec-tivity in a fluvial network for identifying hotspots of geomorphic change. Water Resources Research, 2015, 51(3): 1401–1421
[6] Goren L. A theoretical model for fluvial channel response time during time-dependent climatic and tectonic forcing and its inverse applications. Geophy-sical Research Letters, 2016, 43(20): 10753–10763
[7] Shelef E, Hilley G E. Symmetry, randomness, and process in the structure of branched channel networks. Geophysical Research Letters, 2014, 41(10): 3485–3493
[8] Willett S D, McCoy S W, Perron J T, et al. Dynamic reorganization of river basins. Science, 2014, 343: 1248765
[9] Abed-Elmdoust A, Miri M A, Singh A. Reorganiza-tion of river networks under changing spatiotemporal precipitation patterns: An optimal channel network approach. Water Resources Research, 2016, 52(11): 8845–8860
[10] Ranjbar S, Hooshyar M, Singh A, et al. Quantifying climatic controls on river network branching structure across scales. Water Resources Research, 2018, 54 (10): 7347–7360
[11] Horton R E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geological Society of Ame-rica Bulletin, 1945, 56(3): 275–370
[12] Strahler A N. Quantitative analysis of watershed geomorphology. Eos, Transactions American Geophy-sical Union, 1957, 38(6): 913–920
[13] Shreve R L. Infinite topologically random channel networks. The Journal of Geology, 1967, 75(2): 178–186
[14] Peckham S D. New results for self-similar trees with applications to river networks. Water Resources Re-search, 1995, 31(4): 1023–1029
[15] 柏睿. 大规模河网提取方法与河流结构规律[D]. 北京: 清华大学, 2015
[16] 张丽, 傅旭东, 王光谦, 等. 黄河中游典型河网的结构自相似性. 清华大学学报(自然科学版), 2013, 53(1): 26–30
[17] Tokunaga E. Consideration on the composition of drainage networks and their evolution. Geographical Reports of Tokyo Metropolitan University, 1978, 13: 1–27
[18] Leopold L B, Maddock T. The hydraulic geometry of stream channels and some physiographic implications. US Government Printing Office, 1953
[19] Gupta V K, Mesa O J. Horton laws for hydraulic-geometric variables and their scaling exponents in self-similar Tokunaga river networks. Nonlinear Pro-cesses in Geophysics, 2014, 21(5): 1007–1025
[20] McKerchar A I, Ibbitt R P, Brown S L R, et al. Data for Ashley River to test channel network and river basin heterogeneity concepts. Water Resources Re-search, 1998, 34(1): 139–142
[21] Downing J A, Cole J J, Duarte C M, et al. Global abundance and size distribution of streams and rivers. Inland Waters, 2012, 2(4): 229–236
[22] Ran L, Lu X X, Yang H, et al. CO2outgassing from the Yellow River network and its implications for riverine carbon cycle. Journal of Geophysical Re-search Biogeosciences, 2015, 120(7): 1334–1347
[23] Leopold L B, Wolman M G. River channel patterns: braided, meandering, and straight. US Government Printing Office, 1957
[24] Finnegan N J, Roe G, Montgomery D R, et al. Controls on the channel width of rivers: implications for modeling fluvial incision of bedrock. Geology, 2005, 33(3): 229–232
[25] Pavelsky T M, Smith L C. RivWidth: a software tool for the calculation of river widths from remotely sensed imagery. IEEE Geoscience and Remote Sen-sing Letters, 2008, 5(1): 70–73
[26] Allen G H, Pavelsky T M. Global extent of rivers and streams. Science, 2018, 361: 585–588
[27] Pekel J F, Cottam A, Gorelick N, et al. High-resolution mapping of global surface water and its long-term changes. Nature, 2016, 540: 418–422
[28] 王渺林, 郭生练. 汉江流域水文对气候变化的响应. 水文水资源, 2000, 21(1): 10–12
[29] Lehner B, Verdin K, Jarvis A. New global hydro-graphy derived from spaceborne elevation data. Eos, Transactions American Geophysical Union, 2008, 89(10): 93–94
[30] Bai R, Li T, Huang Y, et al. An efficient and comprehensive method for drainage network extrac-tion from DEM with billions of pixels using a size-balanced binary search tree. Geomorphology, 2015, 238: 56–67
[31] 孔凡哲, 芮孝芳. 利用DEM提取河网时集水面积阈值的确定. 水电能源科学, 2005, 23(4): 65–67
[32] 李照会, 郭良, 刘荣华, 等. 基于DEM数字河网提取时集水面积阈值与河源密度关系的研究. 地球信息科学学报, 2018, 20(9): 40–47
[33] Wang Y, Ni J, Yue Y, et al. Solving the mystery of vanishing rivers in China. National Science Review, 2019, 6(6): 1239–1246
[34] Gupta V K, Ayalew T B, Mantilla R, et al. Classical and generalized Horton laws for peak flows in rainfall-runoff events. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2015, 25(7): 075408
[35] Samal D R, Gedam S S, Nagarajan R. GIS based drainage morphometry and its influence on hydrology in parts of Western Ghats region, Maharashtra, India. Geocarto International, 2015, 30(7): 755–778
[36] Zanardo S, Zaliapin I, Foufoula-Georgiou E. Are American rivers Tokunaga self-similar? New results on fluvial network topology and its climatic depend-ence. Journal of Geophysical Research: Earth Surface, 2013, 118(1): 166–183
[37] Raymond P A, Hartmann J, Lauerwald R, et al. Global carbon dioxide emissions from inland waters. Nature, 2013, 503: 355–359
[38] Wu M, Shi P, Chen A, et al. Impacts of DEM reso-lution and area threshold value uncertainty on the drainage network derived using SWAT. Water SA, 2017, 43(3): 450–462
[39] Ariza-Villaverde A B, Jiménez-Hornero F J, Gutiérrez de Ravé E. Influence of DEM resolution on drainage network extraction: a multifractal analysis. Geomorp-hology, 2015, 241: 243–254
Hierarchical Characteristics of River Network in Hanjiang Basin
HUANG Ziye, WANG Yichu, NI Jinren†
Key Laboratory of Water and Sediment Sciences (MOE), Department of Environmental Engineering,Peking University, Beijing 100871; † Corresponding author, E-mail: jinrenni@pku.edu.cn
The structural characteristics of river network in the Hanjiang basin were investigated based on the extracted high-precision digital river network. Combined with surface water frequency maps and river width remote sensing datasets, we analyzed the self-similarity of geometric and topological structure of the river network, as well as the hierarchical characteristics of river width. The results show that convergences of bifurcation ratio, river length ratio, area ratio, and side-branching ratio happen to rivers at stream-orders 1–6, which implies that geometric and topological self-similarity of river networks was fairly fitted at stream orders of 1–6. Moreover, the statistics of hierarchical characteristics of river width show that within the range of self-similar stream-orders, the average river width presents an approximate exponential distribution. The river width ratio is relatively stable at stream-orders 1-6 and the average value is 1.87, indicating that Horton’s law is applicable to river width. By comparing the river network parameters before and after exclusion of pseudo-rivers, it is found that rivers with smaller stream-order, length, width and basin area are more likely to dry up, leading to the deviations of the real river network from the structure of self-similarity.
Hanjiang basin; river network; stream-order; river width; self-similarity
10.13209/j.0479-8023.2021.009
国家自然科学基金(51539001)资助
2020–02–22;
2020–03–22

