新旧规范中圆形偏心受压构件承载力计算对比分析
林子力,宋煜阳
(云南省交通规划设计研究院有限公司,昆明650041)
1 引言
桥梁结构中,下部结构中多采用圆形柱式桥墩,在永久作用和可变作用共同作用下,墩柱同时承受轴向力和弯矩的共同作用,属于偏心受压构件,在JTG D62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》[1](以下简称“04 规范”)中,采用了迭代或查表的方法计算圆形偏心受压构件的承载能力,而在JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》[2](以下简称“18 规范”)规范中,针对圆形偏心受压构件的承载力计算公式进行了简化,但简化的内容及方式并未做出详细说明。本文从圆形偏心受压构件的计算原理入手,结合04 规范和18 规范中圆形偏心受压构件计算公式,对简化内容和方式进行了理论推导,并结合算例对比新旧两版规范中计算结果的差距。
2 原理推导
桥梁下部结构中所采用的圆形柱式桥墩均沿截面周边均匀布置一排或多排钢筋,理论推导其正截面承载能力时首先需要满足如下假设:截面变形满足平截面假定;构件破坏时截面边缘混凝土极限压应变为0.003 3;受压区混凝土应力分布采用等效矩形应力图形;不考虑拉区混凝土参加受力;假定钢筋为理想弹塑性体[3]。结合以上假定,可以建立圆形偏心受压构件的承载力计算图示,如图1 所示,通过内外力平衡可推导出承载力计算的基本公式。
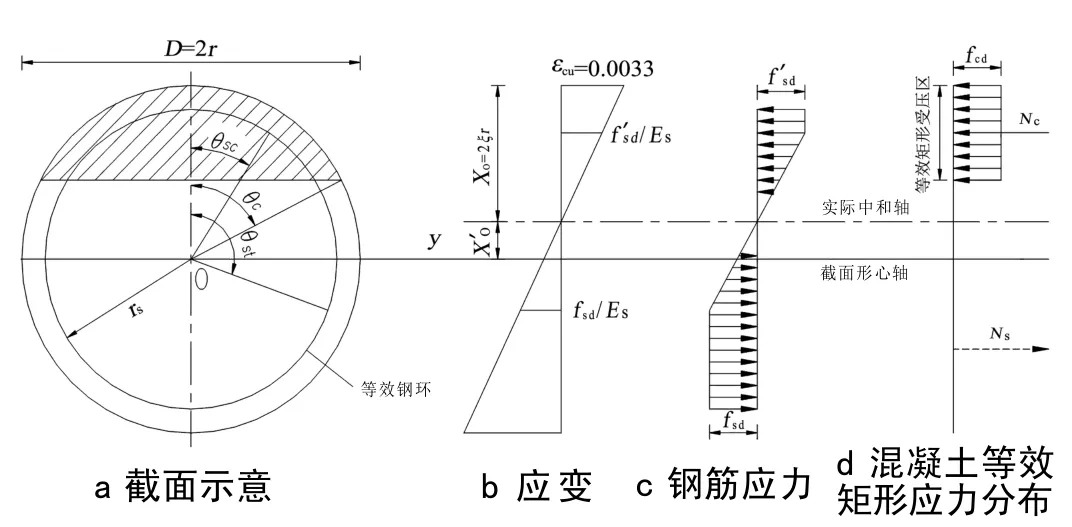
图1 圆形偏心受压构件承载力计算图示
图1圆形截面中阴影面积为混凝土受压区,各参数如图1 所示,其中,D、r 分别为截面直径和半径;rs为等效钢筋环的半径;θsc、θst分别为受拉、受压钢筋屈服的位置;θc为混凝土等效受压面积的圆心角的1/2;x0为受压区高度;ξ 为相对受压高度;εcu为混凝土的极限压应变;Es为钢筋的弹性模量;fsd、fsd′分别为钢筋的受拉、受压设计值;fcd为混凝土的受压强度设计值,Nc、Ns分别为构件中混凝土、钢筋提供的抗压承载力贡献。将均布在墩柱周边的纵向钢筋等效钢筋环,结合钢筋受力状态,钢筋环可分为3 部分:受压屈服部分(0 至θsc)、受拉屈服部分(θst至π)和未屈服部分(θsc至θst)。对上述3 部分进行积分求得钢筋合力Ns和合力矩Ms,然后根据平衡条件可得出圆形偏心受压构件的承载能力,即:

式中,Nu、Mu分别为圆形偏心受压构件的抗压、抗弯承载能力;Mc、Ms分别为构件中混凝土、钢筋提供的抗弯承载力贡献。
3 对比分析
3.1 对比公式(1)中的混凝土合力和合力矩,即Nc项与Mc 项
由18 规范对α 的定义可知:a=2θc/(2π)=θc/π。
经简单公式推导可知,18 规范与04 规范中混凝土合力Nc和合力矩Mc项一致,仅做了形式上的变换,本文不再赘述。
3.2 对比公式(1)中的混凝土合力即Ns 项
由18 规范对α(受压区混凝土截面积圆心角与2π 的比值)与αt(受拉钢筋面积与全部钢筋面积的比值)定义可知,a=2θsc/(2π)=θsc/π,a=(2π-2θst)/(2π)=(π-θ)/π,将上述两式结合04 规范进行变换得:
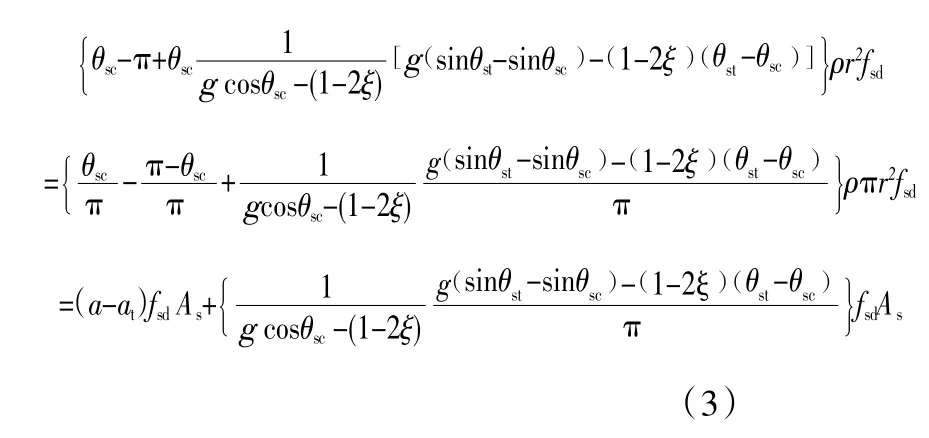
式中,g 为等效钢环半径rs与截面半径r 的比值;As、ρ 分别为纵向钢筋的面积和配筋率。对比可知,对于钢筋部分提供的法向力,相比于04 规范,18 规范仅计入受压屈服和受拉屈服部分钢筋的贡献,对于未屈服部分,即图1 中θsc至θst部分,则认为求合力之后该项较小,可忽略不计。
3.3 对比公式(2)中的混凝土合力即Ms 项
同样,由18 规范对g、α 与αt定义可知:

将上述3 个公式结合04 规范进行变换得:
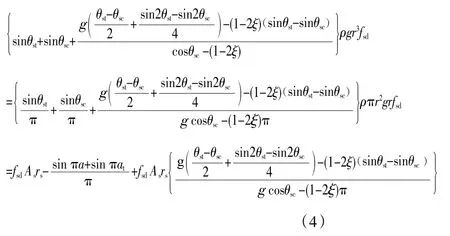
对比可知,对于钢筋部分提供的弯矩抗力,相比于04 规范,18 规范仅计入受压屈服和受拉屈服部分钢筋的贡献,对于未屈服部分,即图1 中θsc至θst部分,则认为求合力矩之后该项较小,可忽略不计。
4 算例
结合理论推导过程,以3 孔18m、桥面宽度为16m 的现浇箱梁为例,对比04 规范与18 规范计算结果的差异。该桥桥面净宽为15.4m,对比计算时上部结构永久荷载相同,可变作用均按照JTG D60—2015《公路桥涵设计通用规范》采用,其中横向按4 车道布置,单车道产生的制动力按照165kN 考虑,车道横向折减系数为0.67。下部结构分别按照直径1.4m、1.7m、2.0m计算,计算位置选择墩底,计算参数及结果对比如表1 所示。
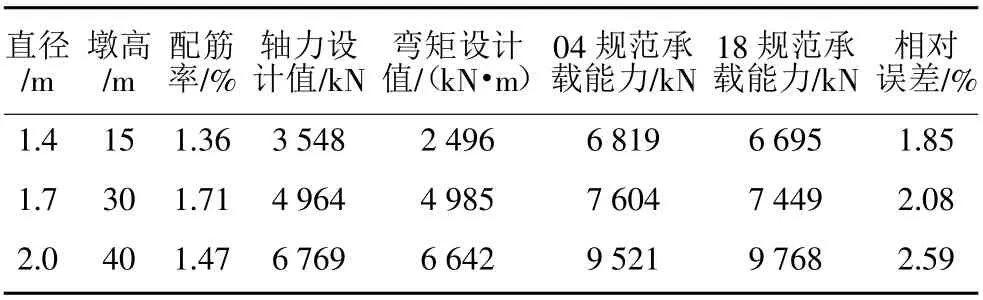
表1 计算参数及结果对比
通过以上算例分析可知,04 规范和18 规范计算所得圆形偏心受压构件承载能力值较为接近,上述算例分析中相对误差均在3%以内。
5 结语
本文结合圆形偏心受压构件计算的基本假定,简要分析了其计算原理,结合04 规范与18 规范中的计算公式进行了推导,为工程师更好地理解规范提供了依据。
推导过程表明:对于混凝土提供承载能力计算,两版规范中仅进行了形式上的变化,其理论计算完全相同;对于钢筋提供的承载能力,相对于04 规范,18 规范中计入了受压屈服和受拉屈服对应区域的钢筋提供的承载力,忽略了未屈服区域钢筋对承载力的贡献。通过算例分析,二者计算结果差距较小,相对误差在3%以内,可认为基本一致,相对于04 规范来说,18 规范的计算公式更有利于工程设计人员理解。

