基于自取法和支持向量机原理的原油管道运行电耗中期预测方法研究

朱振宇 ，白小众，徐磊 ，侯磊 *，刘金海，谷文渊，孙欣

1 中国石油大学(北京)机械与储运工程学院，北京 102249

2 中国石油天然气集团公司油气储运重点实验室，北京 102249

3 国家管网集团北方管道有限责任公司锦州输油气分公司，锦州 121000

我国长输原油管道电耗巨大，年均电耗占管道运行成本的一半以上，降低管道电耗值是管道企业的迫切需要。为此，企业通常采用电耗预测方法对电耗值进行目标管理，即为管道设置合理的电耗目标值。电耗预测按时间间隔可分为短期﹑中期和长期能耗预测3 种类型。对于中期能耗预测而言，其预测周期通常为一个月。预测值与真实值之间的差距既能反映企业的运行管理水平，又能体现管道的节能潜力，因此对原油管道月度电耗值进行准确预测成为一个亟待解决的问题。

原油管道传统的能耗预测方法主要包括工艺计算法和统计预测法[1]。工艺计算法基于管道实际工艺流程进行能耗预测，现多以成熟的商业软件进行仿真模拟。Zuo等[2]根据工艺原理建立了在给定流量下的管道最优运行数学模型，适用于多种原油管道的能耗预测。但该方法通常涉及的站场设备和管道运行参数众多，且理论公式在实际应用时存在局限性；统计预测法基于管道多年历史数据来建立预测模型，隋富娟等[3]利用某输油管道5 年的输油量和油电损耗，建立了三元非等间距的GM(1,1)模型，但原油管道影响因素众多，各因素之间非线性联系强，上述方法不适用于多因素影响下的管道能耗预测。近年来，人工智能技术飞速发展，机器学习方法既能摆脱完全依赖准确理论知识建模的困难，又能基于过程数据对其中蕴含的潜在信息进行挖掘，因此机器学习模型已在多种能源消耗预测领域得到广泛应用。Nasr等[4]利用神经网络模型对黎巴嫩汽油需求量分别进行了单变量和多变量预测，证明多变量模型具有更好的预测效果；王小君等[5]引入基于数据挖掘理论的支持向量机模型，解决了电力系统负荷预测样本选取问题；吕欢欢等[6]针对影响列车牵引能耗因素繁多问题，运用支持向量机和随机森林两种方法建立列车牵引能耗预测模型，有效解决了高维度和非线性难题；Zeng等[7]利用多层感知人工神经网络对某输油管道日耗电量进行预测，证明该模型有较高的预测精度。随着“智慧管道”构想的提出，更加速了以大数据为依托的机器学习技术在管道业的应用与发展，黄维和[8]﹑吴长春[9]﹑董绍华[10]等学者对此作了诸多研究与思考。

利用机器学习方法进行建模，数据的数量和质量是关键[11]，当训练样本数量不充足时，机器学习算法会出现泛化能力不足﹑预测精度不佳等问题。但由于管道运行数据获取成本过高﹑企业重视数据安全﹑因年久失修或者工艺变化而进行管道改造等原因，往往导致难以获得足够多的样本来进行研究。为解决样本不足问题﹑促进管道大数据的发展，本文基于数据生成技术提出通过自取法(Bootstrap)对输油管道运行数据小样本集进行扩充，利用粒子群算法(PSO)优化后的支持向量机(SVM)模型对总体样本进行学习和预测，以此提高预测精度，并以国内某输油管道作为算例分析，验证了该实验方法的可行性与有效性。

1 前期准备

1.1 输入特征选取

选择特征参数的目的是为机器学习方法识别有用和非冗余的特征子集，输入特征参数的合理选择直接决定了模型的预测性能。因此，有必要对管道运行过程中影响电耗的相关因素进行详细分析，选择合适的参数作为预测模型的输入特征。

运行电耗主要是指长输管道各站内的输油泵机组耗电量，这部分能耗是维持管道正常运行最基本﹑最关键的能耗，也最具有节能潜力[12]，主要受原油物性参数﹑管道参数﹑环境参数和运行参数4 类参数影响，部分参数的详细分类如表1 所示。其中，原油物性参数随管道温度变化而变化，在实际运输过程中很难实时获取，且对于同一条原油管道，当输送的油品种类一定时，原油物性的影响可以忽略不计。管道参数基本可以视为固定值，作为输入参数的意义不大。环境参数中地温较为重要，当地温高时管道的散热量会减少，相应的管输耗电量减少，反之则会增加。管道运行参数中的输量﹑进出站温度和压力等参数都与泵机组耗电有着密不可分的联系。基于上述分析，选择输量﹑平均进温﹑平均出温﹑平均进压﹑平均出压和地温作为预测模型的输入参数，用于管道运行电耗预测。

表1 原油管道参数分类Table 1 Classification of crude oil pipeline parameters

1.2 数据来源

管道A为国内一条保温原油管道，全线长度为361.2 km，设计输量为900 万～1000 万t/a，共设有9座站场，为方便论述本文以其中2 座站场数据为例进行实验。取2 站场2017 年1 月至2019 年6 月各30 组数据，其中部分数据如表2 所示。

1.3 抽样方法选取

由于采集的数据样本较少，如果采用传统的随机抽样方法划分数据集，通常会造成得到的训练集和测试集的分布规律与原始数据集的分布规律出现大的偏离，使预测结果缺乏可信度。因此本文采用分层抽样来替代简单随机抽样，用以避免明显的抽样偏差，保证预测结果的有效性。

为验证小样本集下使用分层抽样的优越性，以站场1 的输量数据为例，按其分布规律划分为4 个区间，分别使用分层抽样法和随机抽样法对数据进行抽样，最终的结果如图1 所示。通过分析可得，原始数据中4 个区间所占的比例分别是6.67%﹑26.67%﹑26.67%和40.00%，分层抽样获得的训练样本中四个区间所占的比例分别是4.76%﹑28.57%﹑28.57%和38.10%，随机抽样的结果分别是4.76%﹑23.81%﹑38.10%和33.33%，2 种抽样方法的平均绝对百分误差分别是11.90%和24.71%。由此可知分层抽样方法在小样本情况下能有效降低随机抽样带来的抽样偏差，能够更好地体现原始数据的分布规律，有利于保证预测效果的客观性和可靠性。

表2 站场1 部分数据Table 2 Partial data of Station 1

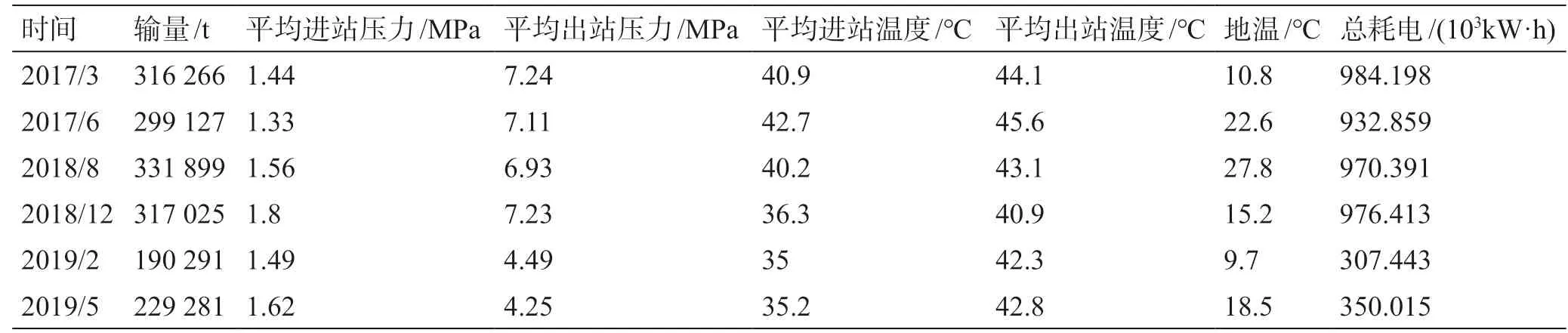
表3 站场2 部分数据展示Table 3 Partial data of Station 2

2 数据生成技术——自取法

充足的训练样本及其在样本空间中的分布性决定了机器学习方法的泛化能力与预测精度，但在实际生产过程中，由于获取样本成本过高﹑数据多但重复﹑考虑数据安全等原因，往往只能获得少量数据，使得建立的预测模型难以达到精度要求。

为此，学者们提出用数据生成技术解决数据不足问题。数据生成技术的思想是利用先验知识或样本分布规律等潜在信息生成新的样本[13]，用于填充样本信息间隔，提高原始样本集的预测能力。生成的新样本被称为虚拟样本或者人工样本，是根据原始样本内的潜在信息而得到的一种新数据。原始小样本﹑虚拟样本和总体空间之间的关系如图2 所示，原始小样本集由少量原始数据组成，总体空间和原始小样本集之间的信息空白则由大量虚拟样本进行填充。因此，原始样本中的信息间隔被缩小，添加虚拟样本能够提高预测模型在小样本集下的学习能力和预测精度。

目前较为常用的生成方法有蒙特卡洛法﹑整体趋势扩散技术(MTD)和自取法等。蒙特卡洛法原理简单，但在数据量极少情况下会产生较大误差[14]；MTD通过三角隶属函数非对称地对数据进行扩散，但有着单模态和独立性假设的缺陷[15]。因此，本文选用自取法作为扩充原始数据的途径，相较于其他方法，它具有不需要对样本分布进行假设的优点，因此当样本分布未知时，该方法最为有效[16-17]。

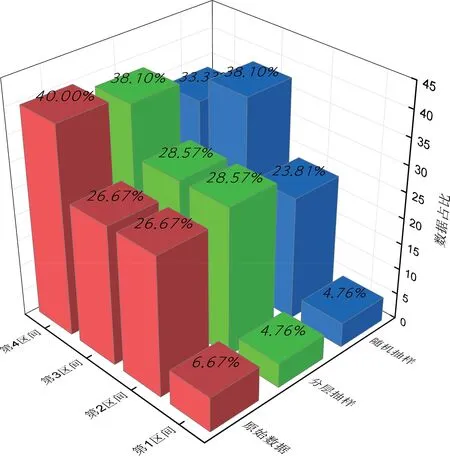
图1 站场1 不同抽样方法抽样结果图Fig. 1 Sampling results of different sampling methods in Station 1

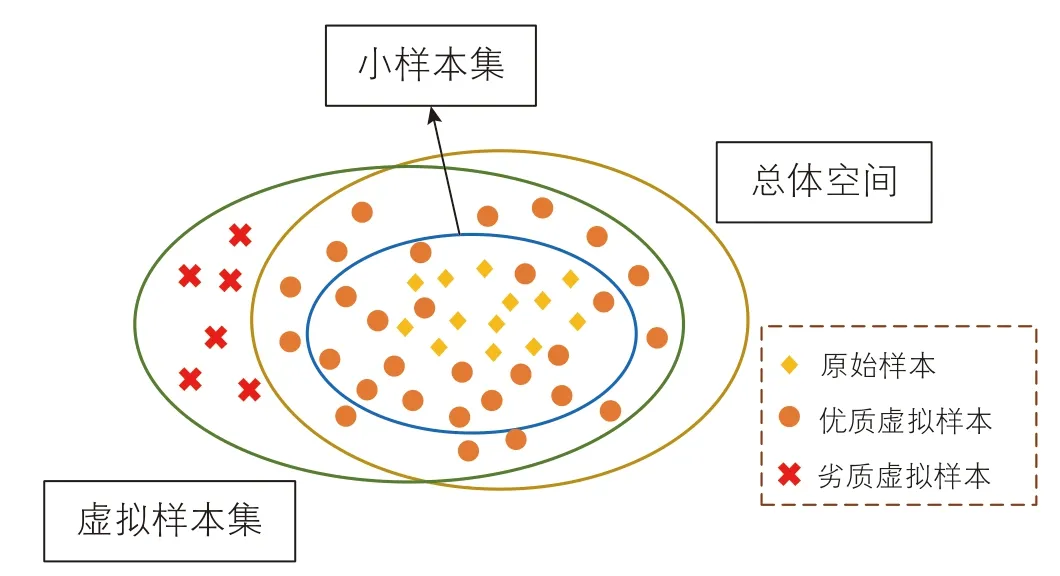
图2 小样本集、虚拟样本 、总体空间关系图Fig. 2 Small sample set, virtual sample, and overall spatial diagram

自取法于1979 年由统计学家Bradley Efron系统地提出，其本质上是一种不需要样本分布假设的非参数采样方法，通过在原始样本的基础上进行随机的有放回的抽样，来构建某个估计量的置信区间。当可利用的样本数量有限时，自取法不需要对经验分布进行过多假设，能够从采集到的新的子样本中得到统计量，从而进一步研究总体样本。该方法实现数据生成过程的步骤如下：

(1)假设原始小样本集X中含有k个特征，n组数据，取出某一特征x=[x1,x2,…,xn],然后使用随机数生成器随机生成整数l1,l2,…,ln∈[1,n]；

(2)在生成的整数l1，l2,…,ln的基础上，根据其所对应的下标，从原始数据集x中进行有放回的抽样，得到新的数据集x’=[xl1,xl2,…,xln]；

(3)重复步骤(2)k次，得到扩充后的样本集X’=[x1′,x2′ ,…,xk′ ]，生成的样本数量为k×n。

3 粒子群算法优化的支持向量机(PSOSVM)预测模型的建立

支持向量机是一种基于结构风险最小化的机器学习算法，相较于神经网络算法，它在处理小样本时能够避免“过拟合”问题，因此被广泛应用于回归﹑预测﹑分类等领域[18-21]。支持向量机的预测精度依赖于惩罚系数C和核参数γ的选取，超参数选取不当会影响模型的泛化能力[22]。因此，需要对这两个超参数进行优化，选择合适的取值。

目前，超参数优化工作主要通过启发式算法来完成，而粒子群算法相较于遗传算法(GA)﹑果蝇算法(FOA)等具有设置参数少﹑收敛快的优点[23]，因此本文选用粒子群算法对支持向量机进行超参数优化。在该算法中，种群由粒子组成，每个粒子的特征包括一个位置向量和一个速度向量，利用个体极值pbest和全局极值gbest来更新位置和速度。每个粒子根据如下公式来更新自己的速度和位置：

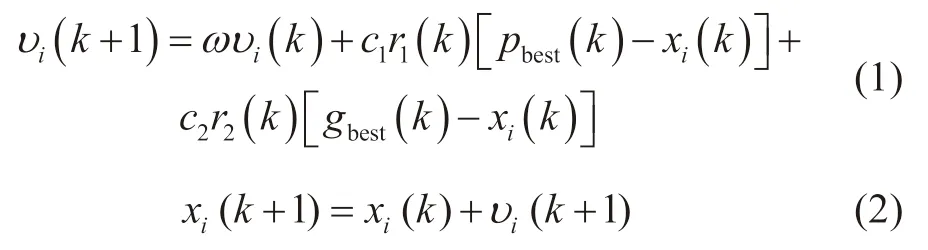
式中，k为迭代次数；ω为惯性权重；c1﹑c2称为学习因子；r1(k)和r2(k)是[0,1]区间的随机数；υi(k)和xi(k)分别表示粒子i在第k次迭代的速度和位置；pbest(k)和gbest(k)分别表示粒子i在第k次迭代的个体极值的位置和全局极值的位置。

提出的PSO-SVM预测模型能够对两个超参数进行动态调整，然后将得到的最优组合反馈给SVM模型，实现超参数的自适应优化，图3 为PSO-SVM模型的超参数优化流程。

4 整体研究框架

本研究的目的是通过增加虚拟样本到特定小数据集来提高预测模型的预测精度，主要内容包括：根据原始小样本集建立初始SVM预测模型；通过自取法生成虚拟样本，对原始样本集进行扩充；将原始样本与虚拟样本合并形成总样本，以此为基础展开预测；对预测结果进行误差分析。具体实现步骤如下：

(1)对搜集的数据进行检查和缺失修补，去除明显错误的数据。

(2)为了避免随机抽样带来的抽样误差，采用分层抽样来划分训练集和测试集，使得划分的样本与初始数据的分布规律较为接近。因为输入值的大小存在较大差异，因此对输入值进行归一化，归一化范围通常为0～1，如式(3)所标。

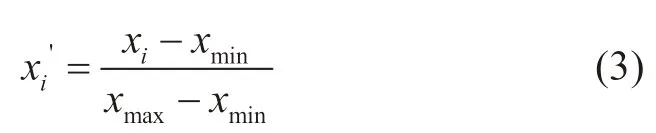
式中，x’是归一化后的结果，xmax和xmin分别是输入数据的最大值和最小值，x是初始值。

(3)利用PSO算法对SVM进行超参数优化，建立初始预测模型，使用原始小样本集中的训练集数据进行训练学习，并在测试集数据上进行测试，记录该模型的预测结果。

(4)通过自取法对训练集数据中的每一个输入属性进行扩充，生成虚拟样本的输入值。

(5)将得到的虚拟样本输入值通过已建立的SVM模型计算得到其输出值。

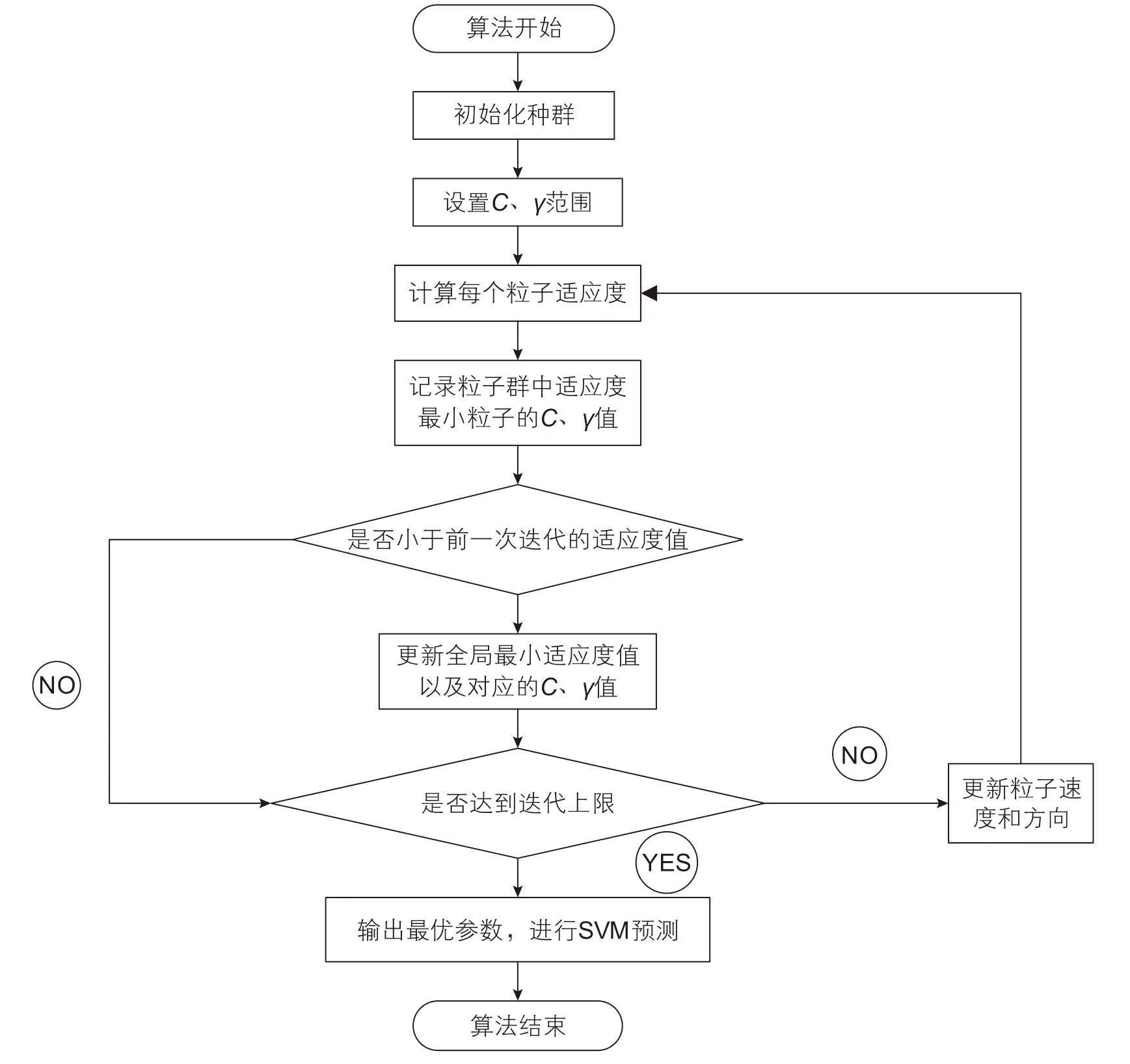
图3 PSO-SVM流程图Fig. 3 PSO-SVM flow chart

(6)重复步骤(4)﹑(5)n次，即可得到n个虚拟样本，将原始训练集数据与虚拟样本合并，得到总样本集。利用PSO-SVM预测模型对总样本集数据进行训练，并在测试集数据上进行测试。将预测结果与步骤(3)的结果进行分析比较，评估该方法的可行性与适用性，图4 为具体流程图。

为了评价预测模型的精度，采用平均绝对误差(MAE)﹑平均绝对百分误差(MAPE)﹑相对误差(RE)和决定系数(R2)作为性能指标来评估各模型的预测能力。各评价指标公式如下：

式中，yi，和分别表示初始值﹑平均值和预测值。

5 算例分析

将所得数据按7:3 的比例进行数据集的划分，归一化后分别进行训练和测试，PSO参数设置如下：C∈[1,9000]，g∈[0.01,10]，最大迭代次数Kmax=100，粒子群数目M=100，粒子维度n=2，加速因子c1=c2=2，适应度函数选择平均绝对百分误差。

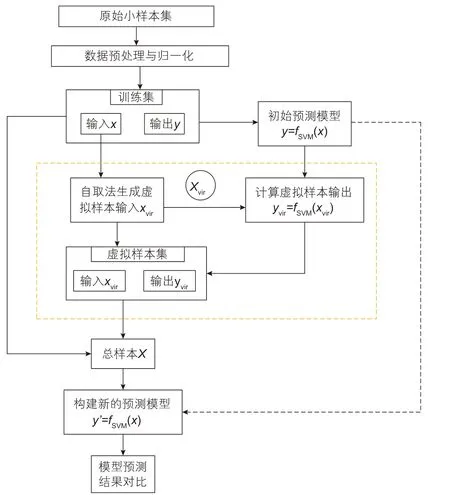
图4 整体流程图Fig. 4 Overall flow chart

支持向量机和神经网络是目前应用较广的两种机器学习算法，为比较二者在小样本下的预测能力，分别利用其对管道数据进行建模和预测，计算得到不同模型预测值的3 种评价指标值，如图4 所示，并以站场1 为例，列举了真实值与预测值比较结果，如表5 所示。分析比较可得，站场1 支持向量机模型的MAE﹑MAPE﹑R2值 分 别 为69.9471×103kW·h﹑4.4701%和0.9279， 相较于神经网络预测的71.2648×103kW·h﹑5.5150%和0.9113，分别优化了1.88%﹑23.38%和1.79%，预测精度更高，得到的预测值更加贴近真实值，验证了支持向量机在小样本情况下能够避免“过拟合”现象，预测效果要优于神经网络算法。

为验证添加虚拟样本对模型预测能力的影响，向已建立的PSO-SVM模型中添加10 组虚拟样本，将预测结果与添加虚拟样本前的预测结果进行对比，图5﹑图6 展示了两站场的测试数据和添加虚拟样本前后的预测值，能够发现添加虚拟样本后的大部分预测值要更接近真实值。为了更清楚地展示添加虚拟样本对预测模型性能的改善，图7-8 分别记录了2 组实验测试集相对误差的绝对值，其基准设置为[0，4%]，通过对比不同模型真实值与预测值之间的偏离程度，能够直观评价模型的预测性能。对于站场1，添加虚拟样本前后的离散点在参考范围内的点数分别为3 个和7个，站场2 中添加虚拟样本前后离散点在参考范围内的点数分别5 个和7 个，证明添加虚拟样本有利于预测模型充分利用原始数据的剩余价值，相较于单纯利用原始样本集，能够提高预测模型的学习能力，有效降低预测误差，保证预测模型在样本不充足时的预测精度。

表4 不同预测模型结果对比Table 4 Comparison of results of different prediction models

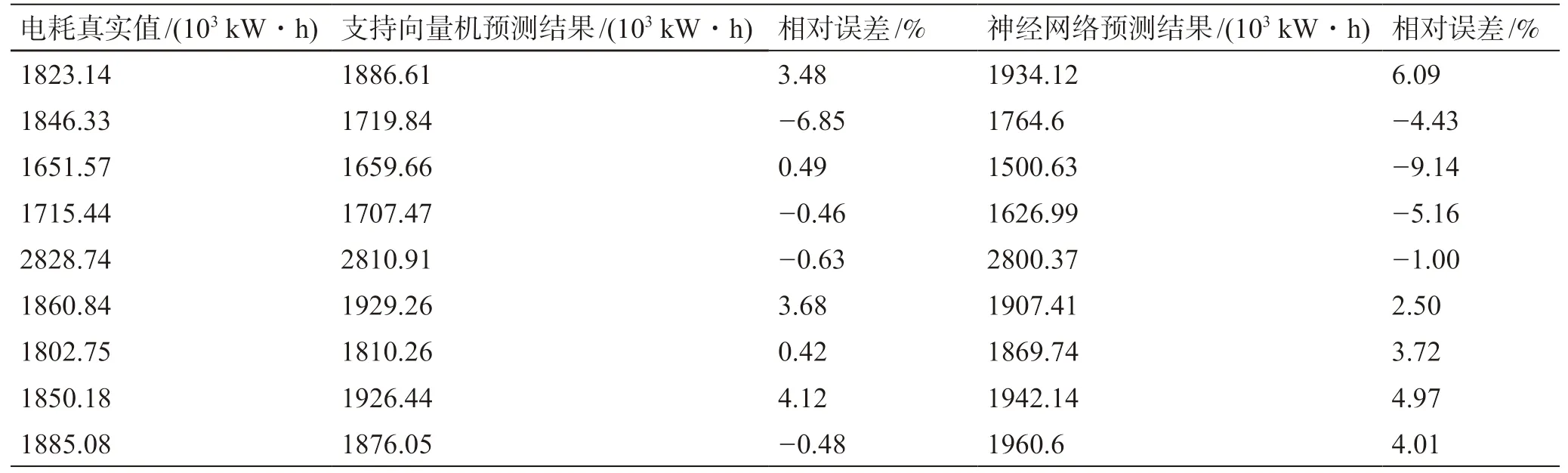
表5 站场1 预测结果比较Table 5 Comparison of predicted results of Station 1

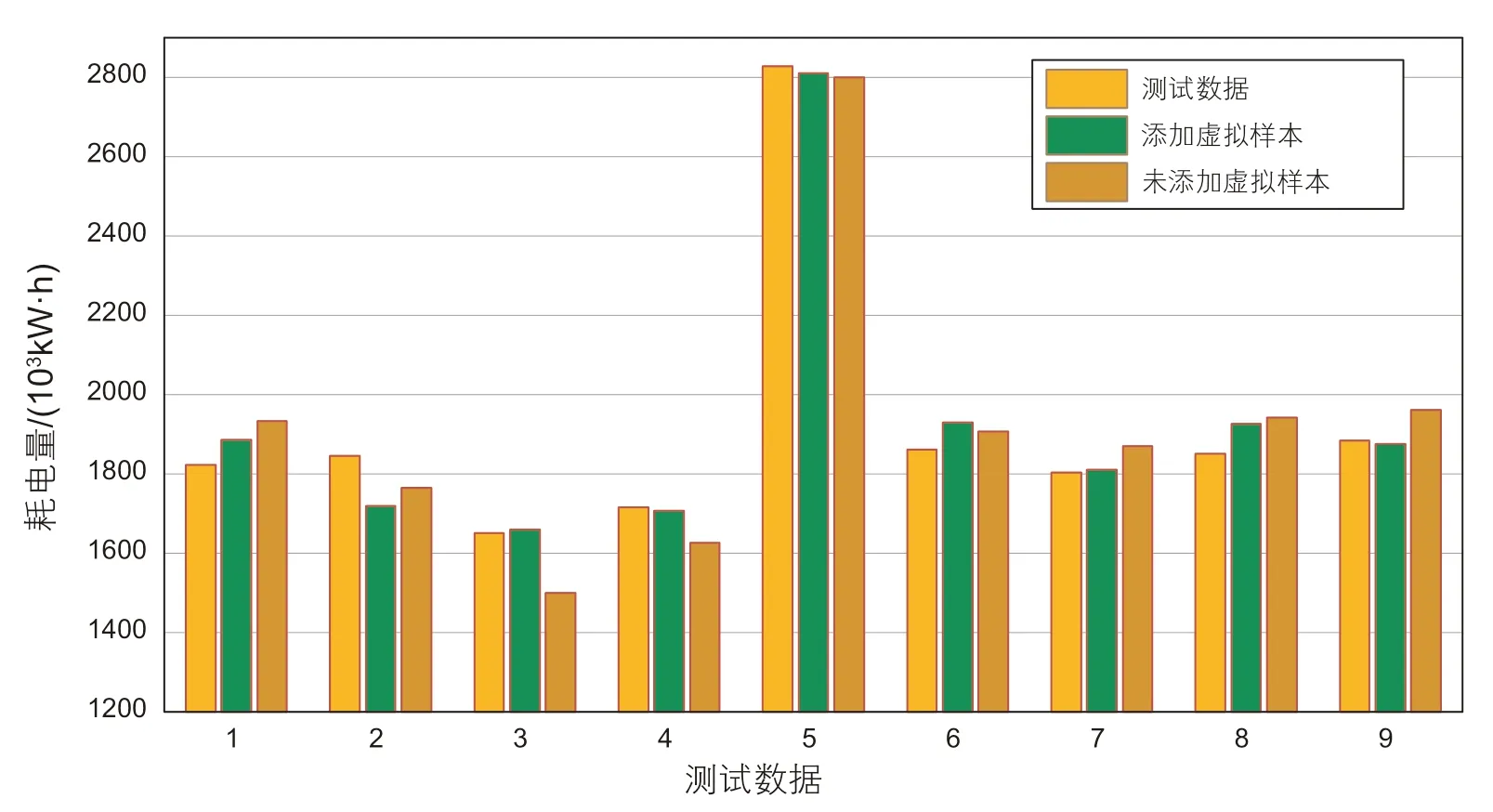
图5 站场1 预测结果对比图Fig. 5 Comparison of forecast results of Station 1

图6 站场2 预测结果对比图Fig. 6 Comparison of forecast results of Station 2

为进一步验证虚拟样本数量对预测结果的影响，向建立好的PSO-SVM模型中依次添加10﹑20﹑30﹑40﹑50 组虚拟样本，分别对测试数据进行预测，将预测结果与未添加虚拟样本的结果进行比较，发现添加虚拟样本后站场1 的MAE值分别下降了19.78%﹑21.17%﹑28.65%﹑30.86%和32.38%，站场2 的MAE值分别下降了12.06%﹑18.43%﹑19.63%﹑25.83%和29.74%，如图9﹑图10 所示。分析可得，随着虚拟样本数目的增加，模型的预测误差在不断降低，但趋势逐渐平稳，说明在一定范围内虚拟样本的加入能够增强模型的学习能力，提高预测精度。但由于实际管道运行数据中仍不可避免的存在部分噪声和冗余，使得模型的预测精度仍具有提升的空间。

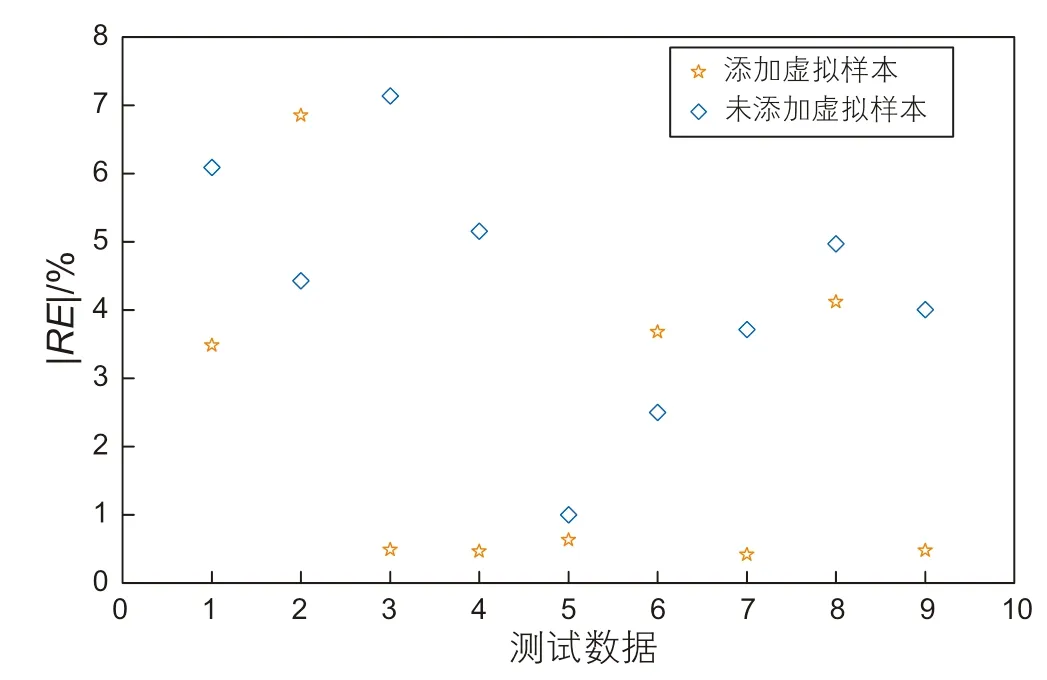
图7 站场1 相对误差绝对值离散图Fig. 7 Discrete figure of absolute relative error in station 1

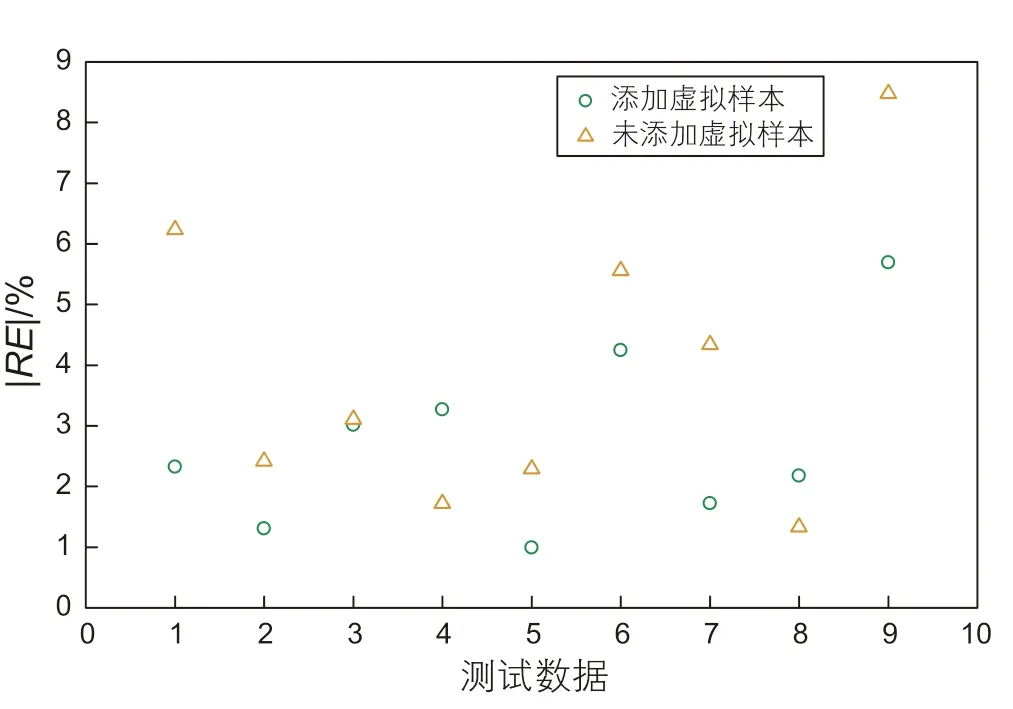
图8 站场2 相对误差绝对值离散图Fig. 8 Discrete figure of absolute relative error in station 2

图9 站场1 不同数目虚拟样本预测误差图Fig. 9 Prediction error graph of different number of virtual samples in Station 1

图10 站场2 不同数目虚拟样本预测误差图Fig. 10 Prediction error graph of different number of virtual samples in Station 2

6 结论

(1)基于数据生成技术与机器学习理论，针对小样本情况下长输原油管道运行电耗中期预测问题，提出利用自取法生成虚拟样本对原始小样本集进行扩充，再利用PSO-SVM模型对耗电量进行预测。实验结果表明，虚拟样本加入后模型的平均绝对误差分别降低了32.38%和29.74%，能够有效降低预测误差，满足生产预测需要的精度，为管道数据获取成本过高﹑企业重视数据安全等原因造成的可用样本不充足问题提供了一种新的解决思路。

(2)通过对比分层抽样法和随机抽样法的抽取结果，证明在小样本情况下分层抽样具有更低的抽样偏差，抽取的训练集和测试集能够更好地反映原始样本数据的分布规律，有利于确保预测效果的客观性和可靠性。

(3)通过对比支持向量机和神经网络两种算法在小样本集下的预测结果，证明支持向量机模型在样本较少时能够有效避免“过拟合”现象，具有更好的预测效果。

(4)通过向测试样本中添加不同数目的虚拟样本来确定虚拟样本最优添加数量，发现随着虚拟样本数目的增多，预测精度逐渐提高，但增幅渐缓，说明一定数目内虚拟样本的加入能够提高模型的预测能力。

(5)提出的虚拟样本方法能够提高预测模型在样本不充足时的预测能力，有利于管道企业对月度电耗值进行精确的目标管理，以便对运行方案进行相应调整，达到降低管道运行电耗的目的。