树枝形专用线取送车作业方案编制优化研究
金启明,李菲菲,刘林忠,张长泽
(兰州交通大学 交通运输学院,1、2、4 研究生,3 教授 博导,甘肃 兰州 730070)
0 引言
树枝形的专用线布置形式在我国铁路运输生产中十分常见,货场和专用线统称为货物作业点(简称为作业点),关于树枝形专用线取送车作业的优化研究已有了一定的成果。唐春林等[1]在考虑调机牵引质量条件下,建立了求解取送顺序的优化模型并使用蚁群混合模拟退火算法求解。郭垂江等[2-4]针对取送顺序优化建立了Hamilton 模型,并分别设计了相应的求解算法。陈利君等[5]利用破圈法等图论知识求解了优化取送顺序的哈密尔顿模型。完整的取送车作业方案包括取送批次、取送时机及取送顺序,而上述文献仅针对取送顺序优化进行研究。李斌等[6]以求解取送批次方案和顺序方案为目的,建立了连送带取作业模式下的数学模型,但考虑到的取送作业模式较为单一。郭垂江[7]从车站作业计划编制系统角度入手,建立基于阶段计划的取送车作业优化模型,但模型没有考虑到装卸区容车能力约束以及调机在取送作业过程中所需要的各种单项作业时间,导致模型存在着一定程度的局限性。
鉴于现有研究中存在的问题,本文针对树枝形专用线取送车作业方案的编制研究,建立了适用于各类取送作业模式下的统一模型,并提出了取送批次、取送时机及取送顺序的的优化方法。
1 优化模型
1.1 问题假设
1)站内仅配备一台取送作业调机;
2)调机在各作业点间的走行耗时为已知;
3)阶段计划内各货物作业点取送车组的详细信息为已知;
4)各车组在货物作业点的作业完毕时刻为已知;
5)阶段计划开始时各专用线的剩余容车空位数已知;
6)所有待取车组在站内的编组时刻已知。
1.2 符号说明定义的参数如下:N 为取送车作业有关的专用线集合,即N={v0,v1,...,vn-1,vn},其中v0表示车站,n为专用线条数;N′为送车作业点集合;N″为取车作业点集合;Nj为第j批次的作业点集合;Nds为调移送车作业点集合;Ndq为调移取车作业点集合;vk、vk'分别为第k次调移作业所对应的调移取车、调移送车作业点;RVK、RVK′分别为vk、vk'在取送顺序方案中的位置。
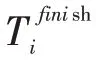
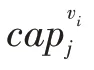
1.3 数学模型由于阶段计划内取送作业内容复杂多样,单一针对某种作业模式建立模型难以适用实际生产,故本文建立如下适用于各类取送作业的数学模型:
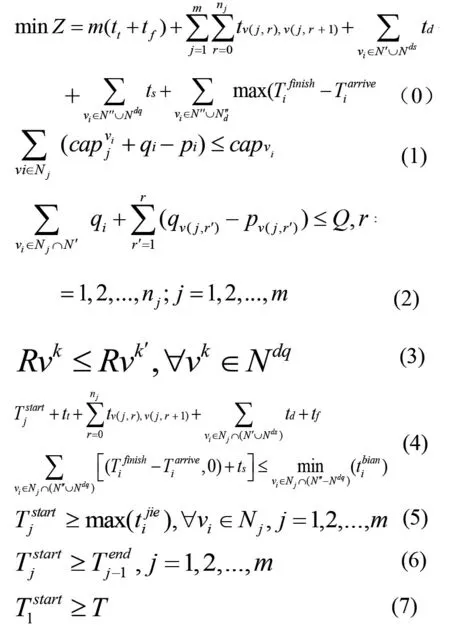
目标函数Z 为阶段计划内的总取送作业时间。式(1)为装卸区容车能力约束;式(2)为调机牵引能力约束;式(3)表示当有调移作业时,调机需先访问调移取车作业点,后访问其所对应的调移送车作业点;式(4)表示每批作业结束时刻不能晚于该批次中所有取车车组最早编组时刻;式(5)表示批次开始时刻不得早于待送车组最晚解体完毕时刻;式(6)表示批次开始时刻不得早于前批作业结束时刻;式(7)表示首批次开始时刻不得早于该阶段计划的开始时刻。
2 取送车作业方案的寻优方法
本文的寻优思路如下:将取送批次划分和取送作业顺序同步优化,然后确定各批次的最佳取送时机。
2.1 各车组最早允许取送作业时间ti对于车站(调车场)中的待送车组,最早可以进行取送作业的时间ti 为该车组在车站(调车场)的解体完毕时刻;对于其他取送作业车组,最早可以进行取送作业的时间ti为该车组在作业点的货物作业完毕时刻。
2.2 取送批次优化
1)构造初始批次方案。将车组所对应的作业点按最早允许的取送作业时间从小到大排列,含调移作业时排序要满足式(3)约束。将每项取送作业单独划分为1 个批次,即批次数m 等于阶段内所有取送作业的数量,这样既可得到一个满足约束式(3)的初始批次方案。例如图1 表示某阶段内包含6 项取送作业的初始批次方案。

图1 某初始取送批次方案
2)取送批次优化。批次优化需在满足约束条件式(2)与(4)的前提下,尽可能地减少批次数。本文设计了逐次合并的批次优化方法,具体步骤简述如下:
Step1初始化批次优化计数器M=1。
Step2 若当前已优化完最后一个批次,转Step4;否则判断批次M 与批次M+1 中的作业是否满足约束(2),若不满足则将不满足的批次移动至该作业点所对应的取车作业批次之后,更新所有批次编号并重新进行Step2;若批次M与批次M+1中的作业均满足装卸区容车能力约束则转Step3。
Step3 将批次M 与批次M+1 合并(记为新的批次M),如果合并的两个批次中含同一个作业点,则将该作业点合为一个作业点。对合并后的批次利用禁忌搜索优化取送顺序,判断是否能够满足约束式(2)与(4),若满足约束则保留新的批次与顺序方案并重新进行步骤Step2;否则不保留本次合并方案,令M=M+1并转Step2。
Step4 批次优化结束。
通过上述步骤划分初始批次即可得到满足约束条件式(1)、(2)、(4)的批次方案。
2.3 取送顺序优化
2.3.1禁忌搜索算法设计
1)解的形式。取送顺序解的形式为一维数组序列,元素从左至右为调机依次访问的作业点顺序。
2)初始解。初始解为批次合并后的顺序方案。
3)邻域结构与领域解。本文所采取的邻域结构是根据2-opt 定义的,即交换某两个元素的相对位置,邻域解的具体构造规则如下:
对于无调移作业或调移作业点对不在同一批次的情况,可随机挑选两个非0 元素互换位置构成新领域解。
对于调移作业点对在同一批次的情况,随机挑选以下规则进行邻域解的构造。
(1)调移取车作业点的移动:将调移取车作业点与其所对应的调移送车作业前的某个元素交换位置。
(2)调移送车作业点的移动:将调移送车作业点与其所对应的调移取车作业后的某个元素交换位置。
(3)非调移作业点的移动:随机挑选两个非调移作业点交换位置。
4)候选集:在生成的邻域解中随机选2nj 个满足约束式(2)的解构成候选集。
5)禁忌表H:禁忌表采用一维数组的形式对禁忌对象进行存储。
6)解的评价函数:本文以取送作业时间作为解的评价值。
7)禁忌长度l:文中各禁忌对象初始的l=2nj。当某禁忌对象重复出现在禁忌表中时增加该禁忌对象的禁忌长度l 以避免陷入局部循环,每重复出现一次l增加2。
8)特赦规则:在迭代过程中遇到所有候选解均在禁忌表中时,选取禁忌表中评价值最好的解进行解禁。
9)终止条件:本文以最大迭代次数3nj 作为算法的终止条件,当迭代次数达到3nj时算法停止迭代。
2.3.2 算法步骤描述
Step1 初始化禁忌表H 为空集;将初始解记为Xnext作为迭代的起点,令Xbest=Xnext。
Step2 根据Xnext 生成候选集,在候选集中挑选评价值最优且不在H中的解记为Xnext。
Step3 将禁忌表中所有禁忌对象的禁忌长度减1,再将禁忌长度为0 的禁忌对象从H 中删除,将Xnext加入到H中并赋予其新的禁忌长度。
Step4 若Xnext 的评价值优于Xbest 的评价值,令Xbest=Xnext。
Step5 若当前满足终止条件则停止计算,输出Xbest;否则返回Step2。
2.4 取送时机优化本文提出临时取送时机和最优取送时机的概念:
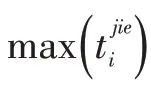
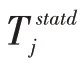
通过利用本文所描述的取送批次、取送顺序、取送时机的优化方法,即可得到满足模型中所有约束条件且取送作业总时间为最小的取送车作业方案。
3 算例仿真
某车站共有10 条专用线呈树枝形布置,具体布置信息如图2 所示。(图中数字为调机的走行时间,单位min。阶段内需完成的取送车作业信息如表1所示,各专用线的剩余容车空位如表2 所示。Q=30,tt=3 min,td=4 min,ts=3 min,tf=2 min。试制定取送车作业方案,使总取送作业时间最小。
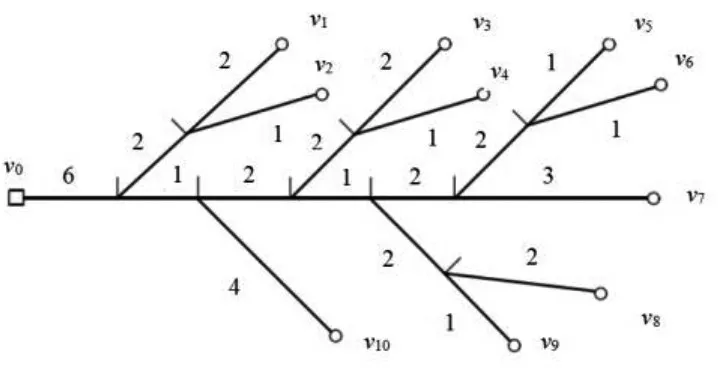
图1 某车站专用线布置示意图
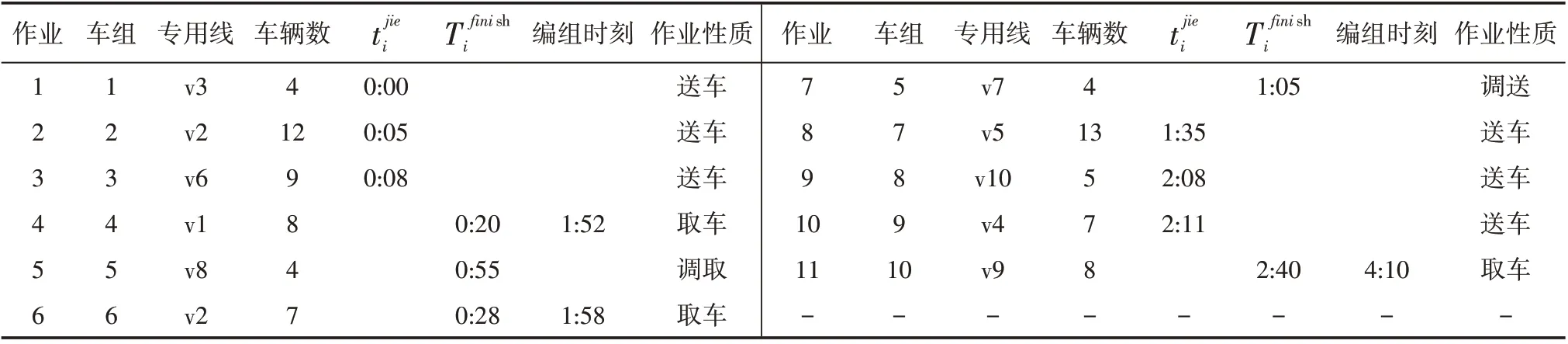
表1 某日0:00至4:00间取送车作业信息

表2 各专用线在阶段计划开始时的剩余容车位
算 例 在Intel Xeon 3.40GHz 的PC 端,运 用Microsoft Visual C++编程进行求解。运行程序求得的最佳结果见表3。从求得的结果可以看出该阶段的取送作业共划分为两个批次:批次1 的开始时刻为0:08,结束时刻为1:40,作业持续了92 min;批次2的开始时刻为2:11,结束时刻为3:21,作业持续了70 min。阶段计划内总的取送作业时间为162 min,程序共运行了10 次,最短运算时长为1.012 s,最长运算时长为1.547 s,平均运算时长1.3 s。通过仿真算例计算结果可看出:求得的取送作业方案符合题目要求,程序的运算时长可以接受。
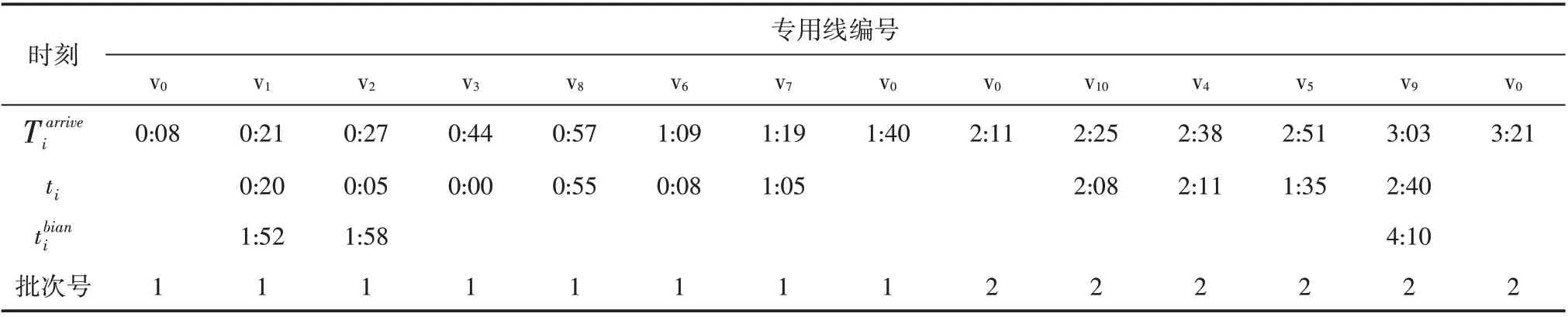
表3 算例仿真结果
4 结论
1)与传统模型相比,本文将取送批次、时机及顺序综合考虑进行优化,同时考虑了货物作业点容车能力、调机牵引能力、每批取送作业最早开始时刻及最晚结束时刻等约束条件,并将调机在取送作业过程中产生的一些单项作业时间纳入模型,使得所建立的模型更符合实际作业要求。
2)本文提出的寻优算法能够在合理的时间内得到较优的取送车作业方案,在保证完成取送任务前提下缩短调机取送作业时间,提高阶段计划内的取送作业效率。

