软、硬地层中局部堆载对隧道横向变形影响的试验研究

梁发云，方衍其，袁 强，李家平

（1.同济大学土木工程学院，上海200092；2.上海申通地铁集团有限公司，上海200070）

随着城市地铁建设规模的不断扩大，各类邻近轨道交通的工程活动愈加常见，地铁隧道临近区域内发生的突发堆载工况也愈加频繁。仅2014年，上海地铁沿线突发堆土便多达16次［1］。因地表超载而导致的地铁隧道安全事故也频频见诸报道。2008年，上海某地铁盾构隧道因突发地面堆土而发生严重渗漏水及结构损伤，部分衬砌环甚至出现混凝土块状脱落及螺栓断裂等现象［1］；2010年，因地表施工倾土而导致上海某地铁隧道在比设计值高6倍的超载下持续运营，并最终导致其水平收敛外径比ΔD/Dt（Dt为隧道外径）高达35.7‰，出现大范围螺栓屈服和漏水现象［2］；2018年，因地表突发6 m超量堆土，某盾构隧道发生最高达27.98 mm的异常沉降，以及累计102处湿渍与14处明显错台［3］。地表堆载作用下，土体应力场发生改变，破坏了盾构隧道原有的平衡状态，致其出现横向变形，严重时会引发接缝超张、管片开裂和螺栓失效等病害，继而导致大面积渗漏水，威胁隧道的正常运营［4-5］。

文献［6-7］对超载工况下不同结构类型的盾构隧道开展了承载能力足尺模型试验，其结果可为隧道结构设计提供一定参考，但试验中用千斤顶等效代替隧道周围土体的荷载效应，没有反映土-结构相互作用。隧道周围土层性质对隧道的受力性能有较大影响，Cui等［8］考虑土与隧道结构相互作用，采用室内平面应变试验研究了水土压力对隧道的横向变形的影响。Atkison等［9］采用模型试验研究无粘性土中隧道的稳定性，获取了地表大面积均布堆载下隧道衬砌结构的内力分布形式。Yang等［10］研究了土体黏聚力、内摩擦角等因素对大面积堆载作用下隧道稳定性的影响。黄大维等［11］借助几何相似比为1：10的缩尺模型，通过开槽法模拟管片接头处刚度折减，研究了软、硬地层中既有隧道在大面积堆载作用下的变形及外表面土压力变化特征。张明告等［12］基于有限元法研究了大面积超载作用下隧道穿越与上覆土层性质对隧道周围土压力与结构变形的影响。Huang等［13］研究了地表超载工况下隧道衬砌结构的弹性变形模式。Yamamoto等［14］研究了地表超载时黏性土层中双方形隧道的稳定性。以上研究主要基于大面积超载情况，然而实际工程中突发堆土的面积较为有限，主要呈局部堆载作用。Huang等［15］研究了软土隧道在不同堆载条件下的变形响应，并指出应尽可能避免偏心局部堆载，但未进行深入研究。吴庆等［16］通过室内缩尺模型试验总结了堆载位置和隧道埋深对盾构隧道横向变形性能影响的规律。孙华圣等［17］在此基础上用有限元进一步定量研究了堆载大小、位置和隧道埋深隧道变形的影响。

局部堆载更能反映工程突发堆土状况，同时周围地层特性对隧道受力与变形的影响也不可忽视。然而目前综合考虑软、硬地层条件和局部堆载对隧道影响的研究较少。本文基于室内缩尺模型试验，研究了不同堆载位置和隧道穿越土层性质下堆载对浅埋地铁盾构隧道的影响。试验过程中测量了隧道的椭圆度、接头张开量及隧道外表面附加土压力的变化情况，揭示了局部堆载作用下隧道的变形机理，从而为后续研究和工程实践提供依据。

1 试验方案

1.1 模型隧道设计

本试验所用模型盾构隧道以几何相似常数Cl=10、重力加速度相似常数Cg=1以及弹性模量相似常数CE=10进行设计［11］。原型盾构隧道为图1所示的某地铁隧道，隧道用通缝拼装，外径为8 000 mm，管片厚度为300 mm，共分5块，管片幅宽为2 000 mm，以C50混凝土浇筑，弹性模量为30 GPa；管片相接处共设6个纵向接头，每个接头均由2根弹性模量为206 GPa的M48环向螺栓连接。

根据几何相似比，计算得模型盾构隧道的外径为800 mm，厚度为30 mm，内径为740 mm，宽度为200 mm。管片单元的分块数量以及位置与原型一致，共由1个封顶管片（圆心角为22.5°）和5个标准管片（圆心角为67.5°）组成，管片用弹性模量3 GPa的有机玻璃加工而成。管片块与块之间设置橡胶件以模拟纵向接缝，并通过模型螺栓将6块管片拼装连成整环，在管片和橡胶件上均预先设置有螺栓孔。

橡胶件等效设计方面：文献［18］的研究表明，原型隧道管片接头抗弯试验测得原型接头抗弯刚度为16.63 kN·m·rad-1，根据抗弯刚度相似条件，试验采用几何尺寸为200 mm×30 mm×5 mm，硬度为邵氏硬度55度的橡胶片模拟接头，其抗弯刚度为1.6 N·m·rad-1。螺栓等效设计方面：原型螺栓弹性模量为206 000 MPa，直径为48 mm，试验中模型螺栓采用304合金刚制作，其弹性模量为194 000 MPa，根据抗拉刚度相似原则［18-19］可计算得所需螺栓断面直径为4.9 mm，因此试验采用两根M5螺栓进行管片拼装。

1.2 模型土配制

黄大维等［20］通过研究指出，在弹性范围内设计模型试验时，模型土的压缩模量需要尽可能满足相似关系，而粘聚力与内摩擦角可不满足相似条件。此外，由于本试验主要研究地表局部堆载下隧道的变形特性，因此土体重度可不必满足严格的相似原则［20］。据此，试验共配制两种模型土，分别为砂土（细砂）和锯末土（细砂+锯末），用于模拟不同土层条件，两者密度分别为1 400和860 kg·m-3，内摩擦角分别为35°和30°。土体压缩模量以压力为10～20 kPa时对应的压缩模量为准，模型中细砂和锯末土分别为2.65和0.85 MPa，相应的原型土压缩模量为26.5和8.5 MPa，分别对应于砂土层和软土层（下同）。

1.3 试验工况设计

本次试验是在同济大学嘉定校区土木工程防灾国家重点实验室的大型土箱中完成，土箱尺寸为4 m长、3 m宽、2 m高。试验模型如图2所示，外部土箱用型钢加工而成，内壁贴橡胶膜。试验中先铺设厚度为0.5Dt（Dt为隧道外径）的细砂作为隧道下卧层，再将隧道模型吊装入模型槽内，随后采用质量控制法［11］逐层填筑厚为0.25Dt的土层，并按要求压实［11］，每加完一层土后静置24 h，以使变形稳定。填土至预设高度后，在预定位置放置铁块，用于模拟地表局部堆载。每次试验分两级加载，每级堆载为2 t重的铁块，铁块底边尺寸为1.2 m×1.2 m，每级加载量为p=14 kPa，总堆载量值为p=28 kPa，可模拟常见的2 m高左右突发堆土。第一级堆载结束后静置0.5 h，进行第二级堆载，再次静置0.5 h后卸载。

为探究隧道所处地层条件对的影响，设计了图3所示两种不同土层分布条件的模型试验，分别模拟隧道穿越砂土和穿越软土，两者分别记为地层1和地层2。为探究地表局部堆载位置对盾构隧道的影响，按荷载与隧道中轴线偏心距e的不同，共设置e=0，200和1 000 mm三种堆载形式，如图4所示。试验详细工况见表1。

图3 隧道穿越土层条件（单位：mm）Fig.3 Situation of tunnel passing through different soil layer(unit:mm)

1.4 传感器设计

试验过程中分别对管片收敛变形、管片接头张开量及隧道外表面附加土压力加以监测。通过测量管径收敛变形可计算得隧道椭圆度，其监测方案如图5a所示，分别在0°、45°、90°以及135°截面布置4个POM-HDQ20-50A电感式位移计，量程为50 mm，精度为0.5%；接头张开量监测方案如图5b所示，管片各接头内、外表面均布置一个应变片，通过测量接头内、外表面变形量可计算接头张开角度；附加土压力监测方案如图5c所示，在管片外表面沿不同角度布置了7个BWM型（微型）土压力传感器，量程为0.02～20 MPa，准确度级别为0.2级。

为验证试验的可靠性，上述传感器分别布置在荷载下方相邻的A、B两个管片上。图6为隧道穿越砂土时，e为0、200和1 000 mm三组工况下A和B截面管径收敛变化情况，由图可知，两管片环相同截面变形量的平均差值仅0.08 mm，说明本试验制模和测试方法较为可靠。处理数据时，取两管片环对应位置数据的平均值作为试验代表值。此外，本试验最终测得的隧道各项变形与力的数据均扣除回填土变形稳定后测得的初始值。

图4 堆载偏心距条件（单位：mm）Fig.4 Eccentric distance of surcharge(unit:mm)

表1 试验工况Tab.1 Test condition

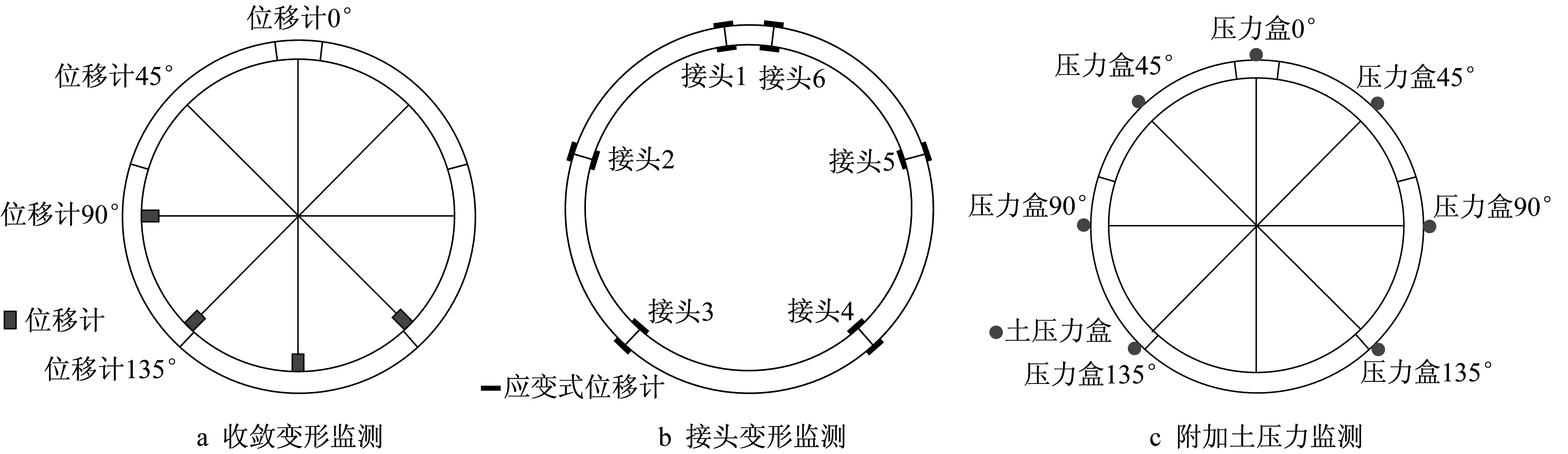
图5 传感器布置Fig.5 Arrangement of sensors

图6 A、B管片环变形对比Fig.6 Comparison of deformation of segment ring A and B

2 试验结果分析

2.1 隧道椭圆度

表2所示为p=28 kPa时隧道管片各截面变形情况，正变形量表示监测截面向外部扩张，负变形量表示监测截面向内部收缩。由表可知，e=0时，隧道竖直截面向内收缩、水平截面向外扩张，收缩量与扩张量大致相当，斜截面的变形量较小，管片呈横椭圆变形。此时砂土层隧道和软土层隧道的水平收敛外径比（ΔD/Dt）分别为6.76‰和15.98‰，大于Huang等［2］调查报道的正常值5.1‰。

表2 p=28 k Pa时隧道管径收敛变形值Tab.2 Convergent deformation value of tunnel diameter at p=28 k Pa mm

通过椭圆度可以定量描述隧道管片变形程度，椭圆度T的计算方法为

式中：T为隧道椭圆度；a为隧道管片变形后长半轴长度；b为隧道管片变形后短半轴长度；Dt为隧道外径。

试验中，通过将加卸载后0°、45°、90°和135°的管径收敛变形值与管片原始外径相加，可计算得管片变形后各方向轴长，取其中最大值为长轴，最小值为短轴，可算得不同堆载位置和地层条件下隧道管片椭圆度的变化情况，如图7所示。根据表2中数据可以计算得到不同堆载位置和地层条件下隧道管片椭圆度的变化情况，如图7所示。砂土层和软土层隧道最大椭圆度分别为12.5‰和31.8‰，大于《盾构法隧道施工与验收规范》［21］规定的限值6‰。随着堆载偏心距的增加，隧道椭圆度先迅速降低然后趋于平缓，p=28 kPa时，当e从0增加到200 mm，砂土层和软土层隧道的椭圆度分别下降了7.4‰和23‰；当e从200 mm增加到1 000 mm，两者的椭圆度又分别下降了3.2‰和5.4‰。此外，e=0、200和1 000 mm时，隧道变形后的长轴方向分别为90°（水平方向）、90°和45°（斜方向），说明堆载偏心距的增加还会导致隧道管片从横椭圆变形逐渐发展为斜椭圆变形，实际工程中应注意调整监测与加固措施。

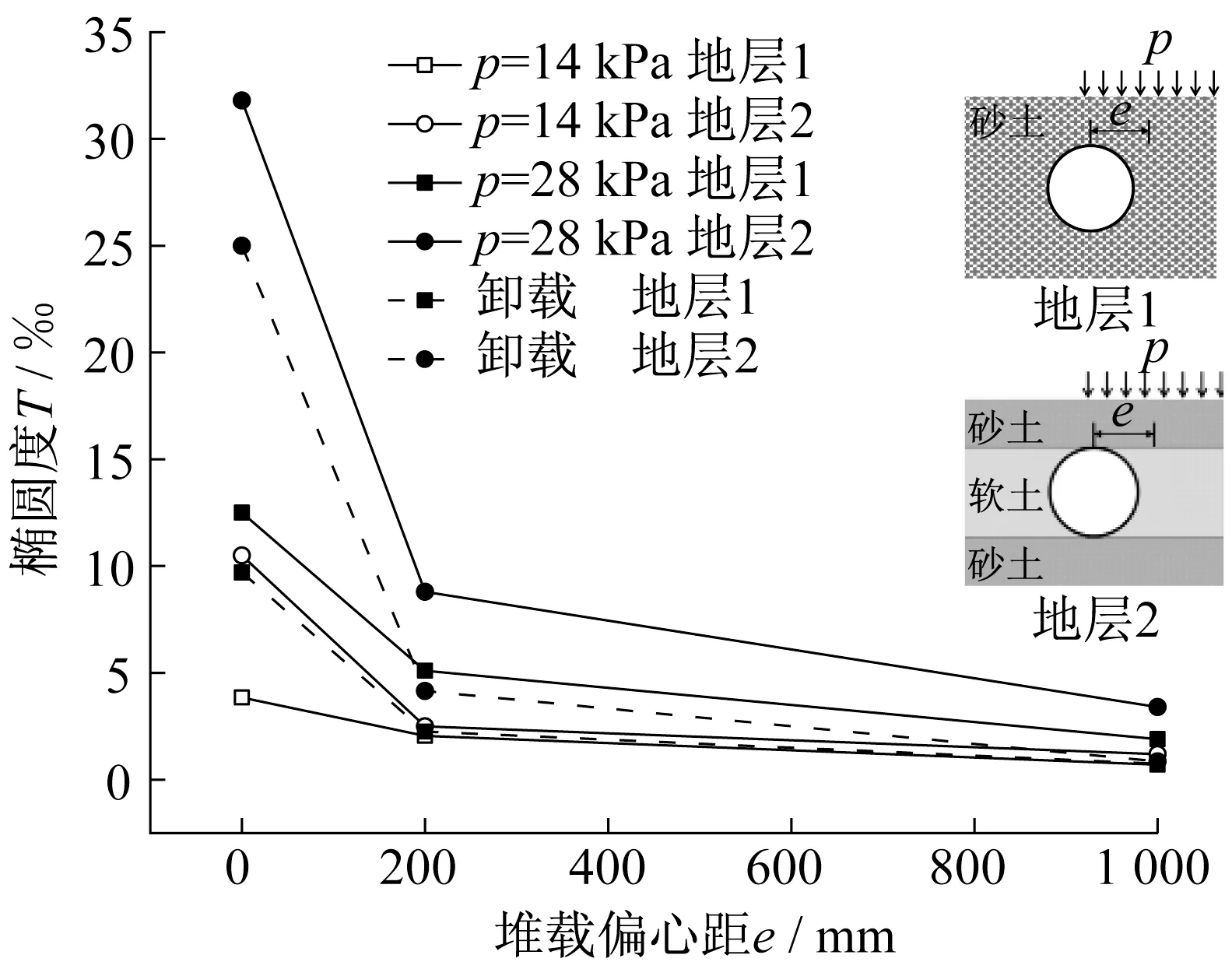
图7 隧道椭圆度Fig.7 Ellipticity of tunnel

对比不同土层特性可发现，软土层隧道的椭圆度普遍大于砂土层，其最大椭圆度为后者的2.5倍，原因是软土可提供的抗力较小，地面堆载作用下隧道结构更容易变形［11］。此外，p=28 kPa时，当e从0依次增加到200和1 000 mm，砂土层隧道椭圆度相对于e=0时依次减小了59%和84%，而软土层隧道椭圆度则依次减小了72%和89%，说明隧道周围土层越软，增大堆载偏心距能起到的保护效果越明显。

分析加-卸载过程发现，卸载后隧道管片仍然有较大的残余变形，此时管片椭圆度甚至大于p=14 kPa堆载下的椭圆度，说明局部堆载对隧道的不良影响难以在卸载后消除。通常来讲，隧道截面的变形主要来自于两个部分：①是管片结构自身的变形；②是管片接头的错台变形［22］。堆载作用产生的附加荷载，不仅使得土层出现塑性变形，而且导致管片间的接头也发生错台变形。两种变形的耦合作用使得卸载后管片产生了不可恢复的残余变形。因此应严格管理邻近隧道各类工程活动，避免因突发局部堆载对隧道造成不可逆损伤。

2.2 接头张开量

通过应变式位移计测量隧道接头内、外表面的变形量，可以计算得各个接头向外张开的角度（外张开量）。

图8所示为不同堆载偏心距时砂土层隧道的接头外张开量（正值表示向外张开，负值表示向内张开）。e=0时，各接头张开角较为对称，隧道肩部接头向外张开，其余部位接头则向内张开，肩部接头（78.75°和281.25°）的外张开角与顶部接头（11.25°和348.75°）的内张开角大致相等，同时上半部分接头的变形量明显大于下半部接头，与王如路等［23］的数值模拟结果类似。随着堆载偏心距增加，隧道接头变形量逐渐减小。此外，e的增加导致了变形的不对称性，e=0时变形主要发生在左右肩部接头和顶部接头，接头变形较为对称，而偏压堆载时变形主要发生在荷载对侧的肩部与顶部接头，两种情况下下隧道接头的变形模式差别如图9所示。

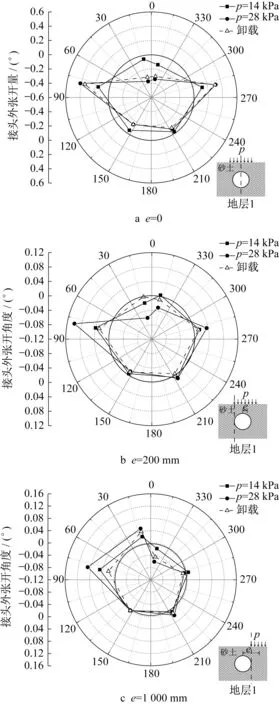
图8 砂土层隧道接头张开量Fig.8 Joint opening of tunnel in sandy soil

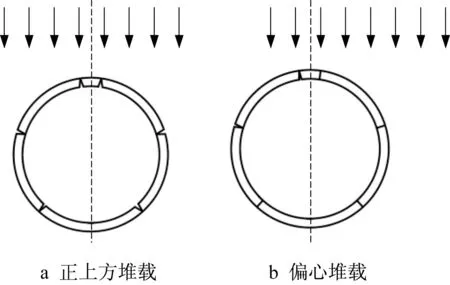
图9 正上方堆载和偏心堆载时隧道接头变形情况Fig.9 Deformation of tunnel joint under direct and eccentric loading

图10 软土层隧道接头张开量Fig.10 Joint opening of tunnel in sawdust soil layer

图10为软土层隧道接头的变形情况，由于变形较大，部分应变位移计遭到破坏，因此仅测得e=0和e=200 mm两种工况下的部分接头变形。对比图8可知，软土层隧道管片接头的变形特征与砂土层隧道类似，但张开量更大。同时，卸载后接头依然有一定的残余变形量，说明本试验中接头变形同样进入塑性发展阶段。王如路等［23］通过数值模拟研究了正上方超载作用下隧道的收敛变形与接头张开量间的关系。结果显示，肩部接头的张开量约为隧道收敛变形量的10%，本试验中e=0时砂土层和软土层隧道肩部接头张开量分别为各自管片收敛最大变形量的4.4%和1.9%，与文献［23］数值模拟结果有一定差异。

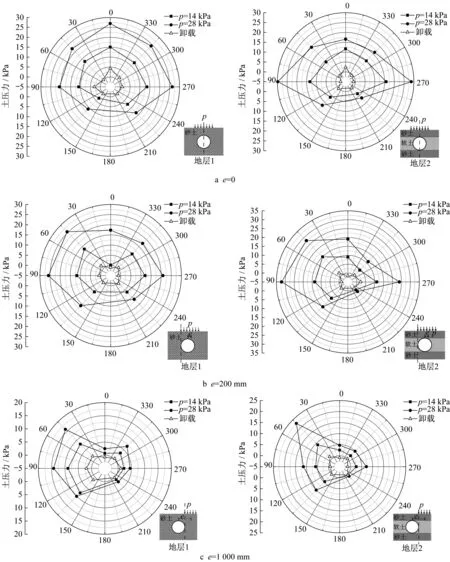
图11 隧道结构外表面附加土压力（单位：k Pa）Fig.11 Additional earth pressure on outer surface of tunnel structure(unit:k Pa)

2.3 土压力

图11所示为隧道外表面的附加土压力分布情况。e=0时，砂土层隧道各方向附加应力分布相对均匀，而软土层隧道附加应力主要集中于水平方向。原因有二：第一，收敛变形更大的软土层隧道土拱效应发挥的程度更大，隧道顶部荷载重分布更明显，因此顶部附加应力减小而水平向应力增大。第二，试验中堆载产生的局部附加应力约为27 kPa，隧道上覆土层自重应力约为7 kPa，对比隧道结构实测附加应力可推测，隧道水平方向的附加应力不仅来自地表局部堆载，还来自水平变形时周围地层对隧道结构的反作用力，而结合图7可知，此时软土层隧道的水平向收敛变形大致为砂土层隧道的2.4倍，因此前者的隧道水平附加应力更大。

堆载偏心距的增加会导致隧道表面的土压力逐渐减小，以及土压力分布情况的改变。为了定量描述土压力向斜截面集中的情况，定义了斜截面土压力集中系数F：

式中：S0，S45，S90，S135，S225，S270，S315分别表示0°、45°、90°、135°、225°、270°和315°截面的附加土压力。

表3所示为加载过程中不同堆载偏心距和土层条件下F的变化情况，e相同时，p为14和28 kPa的F比较接近，说明局部堆载大小主要影响土压力的大小，而基本不影响土压力分布情况。p=28 kPa时，随着e从0增加到1 000 mm，砂土层隧道的F从1.05增加到2.91，软土层隧道的F从1.55增加到3.06，说明堆载偏心距的增加会导致土压力向荷载对侧的隧道斜截面集中。对比不同土层类型可发现，当e=0和200 mm时，软土层隧道的F普遍大于砂土层隧道，而e=1 000 mm时两者的F较为接近，说明小偏心堆载条件下土层性质对隧道土压力分布状况的影响同样不可忽略。

表3 隧道斜截面土压力集中系数Tab.3 Additional earth pressure concentration factor of oblique section of tunnel

3 有限元模拟

3.1 有限元建模

基于商业有限元软件ABAQUS，本文以模型试验为参照建立了图12所示的有限元模型，模型长、宽、高分别为4 000、3 000和1 700 mm。模型四周采用垂直于侧边的滑动约束以限制其水平位移，底部采用固定约束以限制其水平与竖直方向位移［17］。隧道材料采用线弹性模型，土体采用摩尔-库伦弹塑性模型，材料属性同第1.2节模型试验的材料参数。土体采用八节点线性六面体单元模拟［24］，隧道管片基于修正惯用法简化为等效均质圆环并采用八节点六面体单元模拟，隧道外表面与土体之间采用摩擦接触。

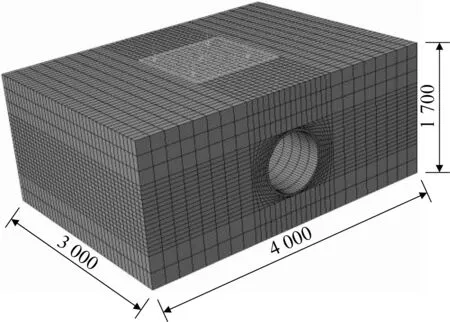
图12 有限元模型（单位：mm）Fig.12 Finite element model(unit:mm)

需要说明的是，本文研究对象为运营阶段的盾构隧道受地表堆载作用下的受力变形特征，而在施工过程中，盾尾注浆层可视为管片结构的附属部分，相比管片钢筋混凝土结构而言，注浆层的厚度相对较小，对于管片结构刚度的影响也较小。因此，本文在有限元建模时，较为充分地参考了已有文献对于类似问题的处理方法［15，17］。而通过忽略注浆层的影响，可以明显提高有限元模拟的计算效率。

图13所示为不同地层条件和堆载位置工况下有限元模拟结果与室内试验的对比情况，由对比结果可知，本文采用的有限元建模方法是可靠有效的。

3.2 参数分析

采用试验①（砂土层隧道，e=0，p=28 kPa）和试验④（软土层隧道，e=0，p=28 kPa）（表1）作为基本模型，通过改变荷载p的大小、堆载偏心距e以及隧道埋深h的量值，对堆载作用下隧道的变形进行参数分析。选用椭圆度T表征隧道整体变形程度，如图14a所示，隧道变形后椭圆度随荷载值的增大而近似呈线性增长，相同荷载下软土层隧道的椭圆度大于砂土层隧道。图14b所示为堆载偏心距和隧道埋深对隧道变形响应的影响，随着堆载偏心距增大，隧道椭圆度显著减小。然而，埋深较大的隧道在受荷后仍发生较大变形，进一步说明地表突发堆载对隧道运营安全的较大威胁，隧道维保工作中应对这一风险源引起足够高的重视。

综上所述，软土地区地铁隧道运营过程中应警惕各类突发地表堆载，若确需堆土，则应尽可能避免隧道正上方超量局部堆载，做到“预防为主、少堆远堆、提前保护、实时监控”。

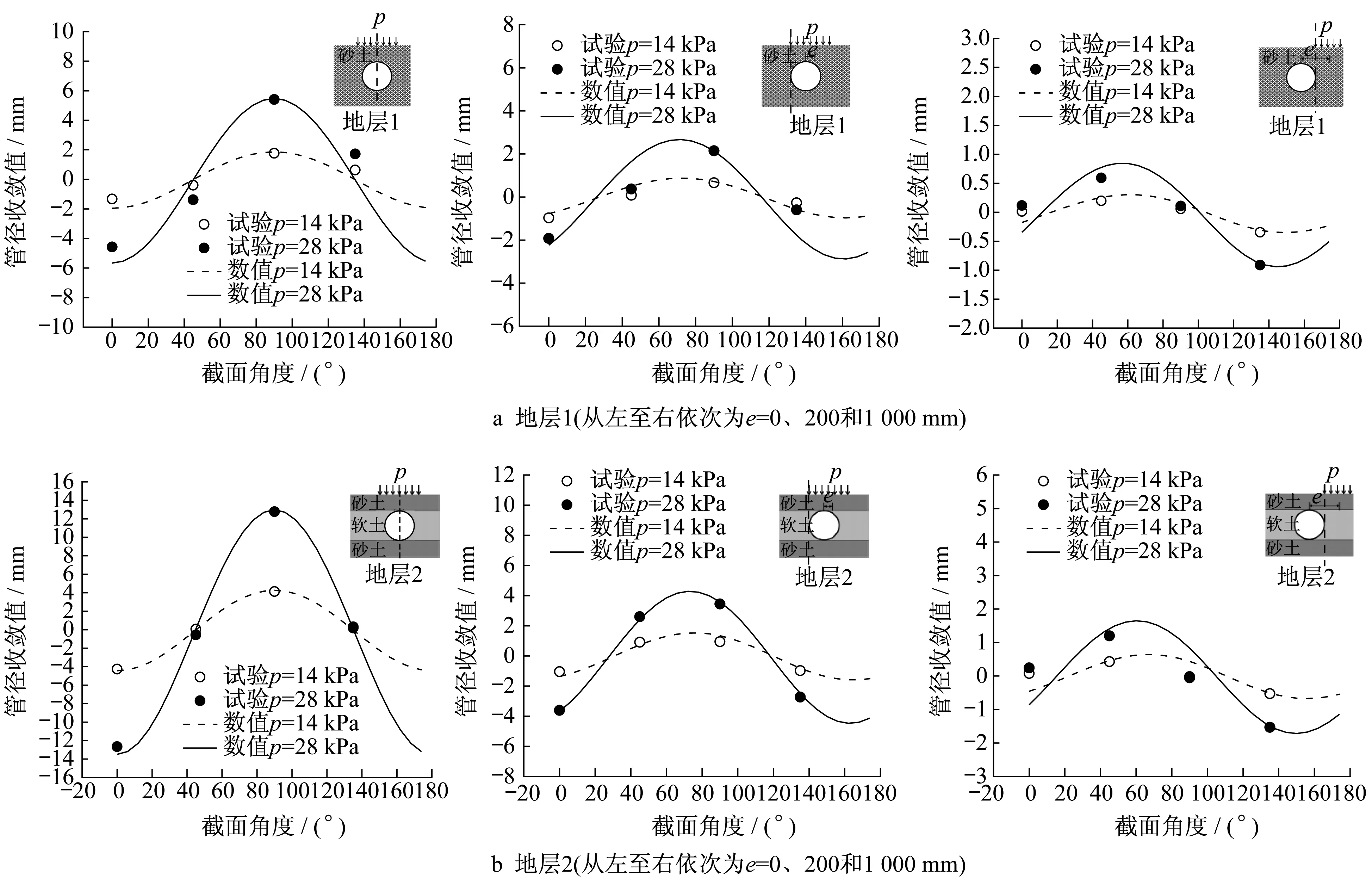
图13 有限元与试验结果对比Fig.13 Comparison of finite element method and experimental results

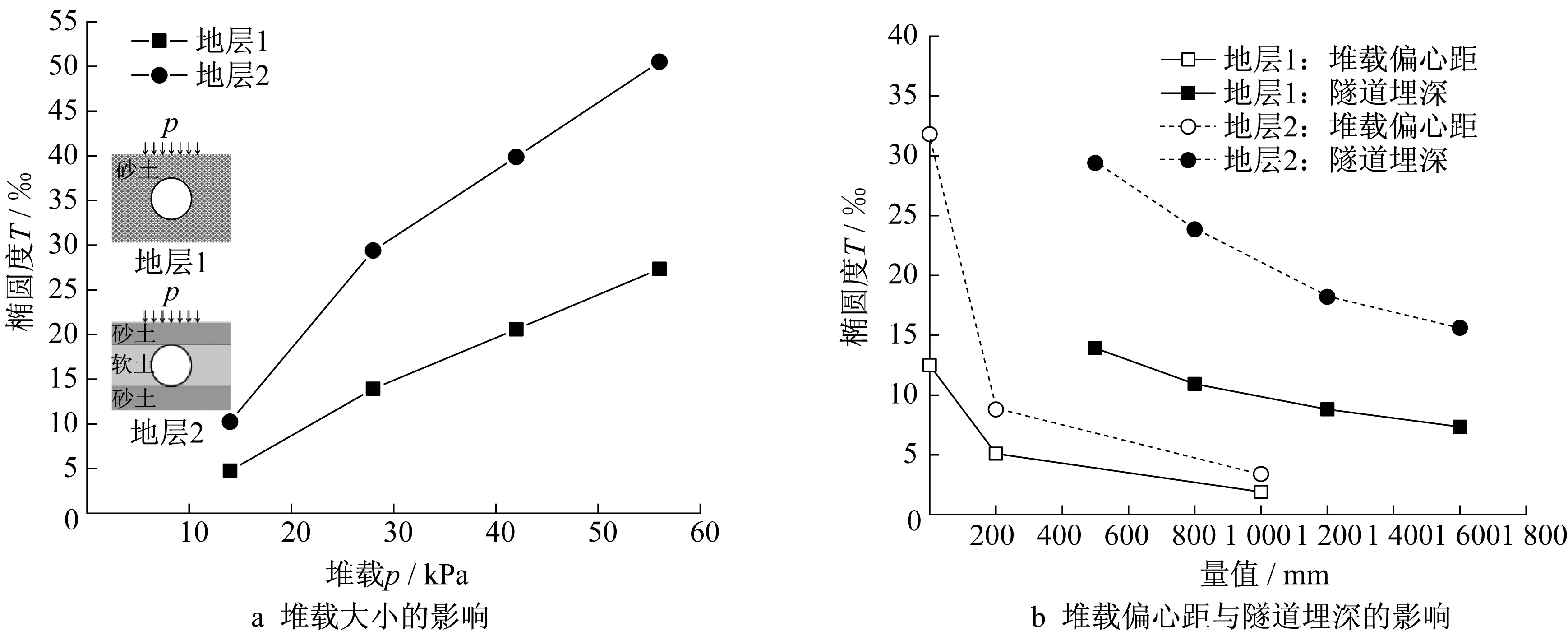
图14 参数分析Fig.14 Parameter analysis

4 结论

本文采用室内模型试验研究了地表局部堆载下软、硬土层中地铁隧道的横向变形性能，通过控制堆载偏心距和隧道穿越土层压缩模量的变化，对比分析了不同工况下隧道椭圆度、接头外开量和外表面附加土压力的变化情况，主要结论如下：

（1）随着堆载偏心距的增加，隧道椭圆度先迅速下降然后趋于平缓，并且从横椭圆变形逐渐转变为斜椭圆变形。软土层隧道的椭圆度比砂土层隧道更大，并且增加堆载偏心距后软土层隧道椭圆度的减小比砂土层隧道更明显。

（2）增加堆载偏心距可以减小隧道接头变形量，正上方堆载时变形主要发生在隧道左右肩部与顶部接头，且较为对称，偏压堆载时变形主要发生在荷载对侧的肩部与顶部接头。软土层隧道接头的变形量比砂土层隧道更大。

（3）堆载作用下硬土层隧道附加土压力分布相对均匀，而软土层隧道附加土压力主要集中于水平方向。随着堆载偏心距增加，附加土压力逐渐减小，且压力主要集中点向荷载对侧的斜截面转移。地表突发局部堆载容易对隧道造成较大损伤，且这些损伤难以在卸载后恢复。

作者贡献申明：

梁发云：提出研究课题，指导撰写论文，审阅修订论文；

方衍其：实施试验研究，处理试验数据，撰写论文；

袁强：设计试验方案，实施试验研究；

李家平：提供研究思路和技术指导。