前向安全的格基代理签名
谢 佳 胡予濮 江明明
1(河南财经政法大学计算机与信息工程学院 郑州 450046) 2(综合业务网理论及关键技术国家重点实验室(西安电子科技大学) 西安 710071) 3(淮北师范大学计算机科学与技术学院 安徽淮北 235000)
(xiejia199325@163.com)
1996年Mambo等人[1]首次提出代理签名这一概念.在代理签名模型中,原始签名人委托代理人进行签名,签名验证者能够有效区分当前签名来自代理签名人还是原始签名人.由于其在移动通信、分布式系统和电子拍卖等领域的广泛应用[2-5],2003年前后,各种代理签名[6-9]如雨后春笋般涌现.然而,量子计算机的出现使得我们对代理签名的安全性有了更高的要求.2010年Jiang等人[10]首次利用盆景树模型构造了格基代理签名方案.该方案在标准模型下代理签名人不能伪造原始签名人进行签名权力委托,但原始签名人却可以成功伪造出代理签名者的签名.2011年夏峰等人[11]和Wang等人[12]同样使用盆景树模型构造了格上代理签名方案.为了克服格维数随代理权利委托逐渐增大的问题,Kim等人[13]使用格上固定维数的委派技术构造了格上高效的身份基代理签名方案.随后,更加高效的格基代理签名方案[14-16]相继被提出.
在传统的签名方案中,一旦签名密钥暴露,签名就变得不可信任,无论该签名来自密钥泄露事件之前还是密钥泄露之后.为了解决这个问题,1997年Anderson[17]提出了前向安全签名的概念.前向安全签名,顾名思义,即使暴露当前时段签名密钥,也不会影响之前签名的有效性.因而,前向安全签名可以减少密钥暴露的威胁.前向安全的签名方案大致可分为2类:1)常规前向安全签名[18-21];2)具有特殊性质的前向安全签名,如身份基前向安全签名[22-24]、前向安全阈值签名[25-26]、前向安全代理签名[27-32]、前向安全群签名[33-37]、前向安全的序列聚合签名[38]等.
由于兼顾可代理和前向安全的优势,前向安全的代理签名自提出以来得到了快速发展[27-32].然而,现存的前向安全代理签名大都基于离散对数或整数分解问题,而Shor[39]早在1997年已经指出,经典数论问题(大整数分解和离散对数问题)在量子计算环境下已不再安全.随着量子计算机的逐渐推广,寻找量子免疫的前向安全代理签名就显得尤为迫切.
幸运的是,格公钥密码以其存在任意实例到最坏实例的规约、计算简单高效(格基密码的相关运算只是简单的矩阵向量乘法和模加法)、能抗量子攻击等诸多优势,成为后量子时代密码算法的不二选择.因而,基于格基困难问题构造前向安全代理签名可能会是一个很好的尝试.
本文的主要贡献有2个方面:
1) 基于格上的小整数解问题,我们提出了首个随机预言机模型下前向安全的格基代理签名;
2) 借助于格基委派技术和消息添加技术,我们构造了标准模型下前向安全的格基代理签名.
1 预备知识
本节我们将对文中用到的一些符号和参考文献中已知的一些结论作出说明.
1.1 基本定义

1.2 格的相关知识
定义1.格.已知矩阵B=(b1‖b2‖…‖bm),b1,…,bm∈Rn为m个线性无关向量,则由B生成的格Λ为
其中,格Λ的秩、格Λ的维数分别为m和n,B为格Λ的一组基.


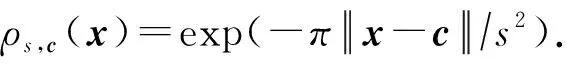
DΛ,s,c(x)=ρs,c(x)ρs,c(Λ),
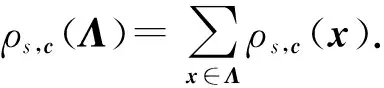
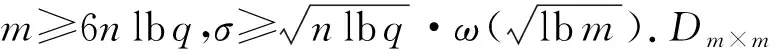
引理1.给定任意实数σ>0,正整数m,有:
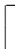

1) 存在1个PPT算法SampleD(A,T,σ,c)能够输出一个分布统计接近于DΛ⊥(A),σ,c的向量v;
2) 存在一个PPT算法SamplePre(A,T,σ,u)能够输出一个分布统计接近于DΛu(A),σ的向量v.
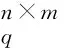
2 前向安全代理签名的定义
本节我们将对前向安全代理签名的定义以及安全性证明作出阐述.
定义6.前向安全代理签名方案.1个完整的前向安全签名方案由7个多项式时间算法构成:系统建立算法Setup、密钥生成算法Keygen、代理委派算法Delegate、委派认证算法D-Verify、密钥更新算法KeyUpdate、代理签名算法ProxySign和签名验证算法ProxyVerify.
1) Setup.输入安全参数n,密钥生成中心(KGC)运行该算法生成并输出系统公共参数PP.
2) Keygen.输入公共参数PP,KGC运行该算法输出原始签名人Alice的公私钥对(ska,pka)和代理签名人的公私钥对(skb,pkb).
3) Delegate.为了将签名权利委派给代理人Bob,原始签名人Alice以自身私钥ska和Bob的身份idb为输入,运行该算法生成代理签名私钥SKid|0并将该私钥发送给Bob.
4) D-Verify.接收到SKid|0后,Bob验证其是否为Alice的合法委派私钥,若否,则返回至上一步继续请求委派.
5) KeyUpdate.输入当前时间i、代理签名者身份idb以及之前时段的代理签名私钥SKid|i-1,该算法输出当前最新的代理签名私钥SKid|i.
6) ProxySign.输入签名消息m和当前时间i,Bob利用代理签名私钥SKid|i生成签名sigi,并将sigi作为m的代理签名.
7) ProxyVerify.以(sigi,m)为输入,当且仅当sigi为消息m的合法签名时,算法输出为“1”;否则输出“0”.
定义7.正确性.定义6的前向安全代理签名方案中,签名方案满足正确性是指ProxyVerify(sigi,m,id,i)能以压倒势的概率输出“1”.
定义8.不可伪造性.考虑前向安全代理签名方案的不可伪造性时,往往有2种安全威胁要考虑:
1) 敌手A1,即未被授权的代理签名人想要模仿被授权的代理签名人进行签名;
2) 敌手A2,即恶意的原始签名人试图代替代理签名人完成代理签名.
对于任意多项式时间的敌手A1和A2,挑战者能够赢得以下游戏(游戏由Setup,Queries和Forgery三个步骤组成)的概率均为可忽略时,我们称该方案是不可伪造的,且是前向安全的.
1) Setup.挑战者C运行方案的初始化算法,生成系统公共参数PP,并将其向敌手公布.
2) Queries.在询问阶段敌手可作3个询问.
① DelegateQuery.当敌手发送代理签名者身份id作委派询问时,挑战者C生成相应的代理签名私钥SKid|0并将其返还给敌手.
② BereakinQuery.当敌手发送时段j,代理签名者身份idb作询问时,挑战者C生成当前时段的代理签名私钥SKid|j并将其返还给敌手.
③ ProxySignQuery.当敌手发送(id,i,m)作代理签名询问时,挑战者C生成当前时段的代理签sigi并将其返还给敌手.
① 1≤t* 3) Delegate.为了将签名权利委派给代理人Bob,原始签名人Alice计算H(ida|idb|0)=R0=Ra→b|0.随后Alice运行引理6中的格基委派算法BasisDel(A,R0,TA,σ0)生成并输出Ta→b|0=[t1‖t2‖…‖tm]作为Alice授权给Bob的代理签名密钥. 6) ProxySign.输入签名消息m,Bob计算μ=H1(ida|idb|m|i),随后运行引理3中的原像采样算法得向量ui←SamplePre(Aa→b|i,Ta→b|i,si,μ)和vi←SamplePre(Bb|i,Tb|i,si,μ).最后,Bob输出(ui,vi)作为当前时段对消息m的签名. 7) ProxyVerify.接收到签名之后,验证者首先计算矩阵Ra→b|i=H(ida|idb|i)…H(ida|idb|0)和矩阵Rb|i=H(idb|i)…H(idb|1),μ=H1(ida|idb|m|i).算法输出为“1”,当且仅当: 定理1.3.1节构造的格基前向安全代理签名满足正确性. 证明. 假设(ui,vi)为对消息m的签名,由ProxySign可知ui,vi分别来自2个原像采样算法,即由SamplePre(Aa→b|i,Ta→b|i,si,μ)求得ui以及vi←SamplePre(Bb|i,Tb|i,si,μ).由引理3可知ui和vi分别服从分布DΛμ(Aa→b|i),si和DΛμ(Bb|i),si.因而可得Aa→b|iui=μmodq,Bb|iui=μmodq.由KeyUpdate以及引理6可知: A(H(ida|idb|i)…H(ida|idb|0))-1= 证毕. 定理2.假定格上的SIS问题在多项式时间算法攻击下是困难的,则以上格上的前向安全代理签名方案在随机预言机模型下是存在性不可伪造的. 引理7.假定格上的SIS问题在多项式时间算法攻击下是困难的,则3.1节构造的格前向安全代理签名方案在类型1敌手攻击下是存在性不可伪造的. 调用:调用格上的SIS问题实例,模拟器C需要返还一个合法的解. 首先,我们假设3个条件成立: 1) 对于每一个时间段i=0,1,…,T-1,敌手A1可以适应性地对任意身份作多项式次H询问; 2) 对于任意的j 3) 在对任意签名人作签名私钥询问之前,假定A1已经预先完成相关的H和H1询问. Queries.当敌手A1伪造签名时,假设C随机选择i*(1≤i*≤T-1)作为伪造签名的时段.敌手A1可以适应性地作询问: 1)H-Oracle-Query.对于任意的时间i=0,1,…,T-1,A1可以适应性地对任意身份作H询问. 模拟者C维持一个列表L1={ida,idb,i,Ri}.输入身份和时间的一组数据(ida,idb,i),C首先在列表L1中查找(ida,idb,i).若(ida,idb,i)已存在于L1中,则模拟者C返还相应的Ri给敌手A1.否则,C从Dm×m中选择1个矩阵Ri并存储(ida,idb,i,Ri)在列表L1中.最后,模拟者C返还相应的Ri给敌手A1. 2) DelegateQuery.模拟者C维持1个列表L3={ida,idb,0,Ta→b|0}.假定Q表示敌手能够作委派询问的最大次数,敌手A1随机选择l∈{1,2,…,Q},C所作回应如下: 如果idb并非第l次委派询问,则C回应如下.输入身份和时间的一组数据(ida,idb,0),C首先查找列表L1找到其对应的Hash值R0并运行BasisDel(A,R0,TA,σ0)生成Ta→b|0.最后,模拟者C将(ida,idb,0,Ta→b|0)存储在列表L3中,并将Ta→b|0发送给A1. 如果idb刚好是第l次委派询问,则C终止操作. 3) KeyUpdateQueries.C维持列表L4={ida,idb,i,Aa→b|i,Ta→b|i,Bb|i,Tb|i}.当敌手A1发送(ida,idb,i)作签名私钥询问时,C所作回应为: 如果idb刚好是第l次委派询问,则C回应为: ③ 如果i*+1 4)H1-Oracle-Queries.C维持列表L5={ida,idb,i,m,ui,vi,Aa→b|iui}.当敌手A1发送(ida,idb,i,m)作H1询问时,C所作回应如下:如果L5列表中已经存在(ida,idb,i,m),则将其对应的Aa→b|iui作为其Hash值H1(ida|idb|m|i)发送敌手;否则,C在列表L1,L2和L4中分别查找H(ida|idb|i),H(idb|i))和(ida,idb,i,Aa→b|i,Ta→b|i,Bb|i),然后模拟者计算ui←SampleDom(1n)以及Aa→b|iui,由于A1知道TB,在做完H询问后敌手A1可知Tb|i,而后计算vi←SamplePre(Bb|i,Tb|i,Aa→b|iui,si).最后,模拟者将(ida,idb,i,m,ui,vi,Aa→b|iui)存储于列表L5中,并将Aa→b|iui作为其Hash值H1(ida|idb|m|i)发送敌手A1. 5) ProxySignQueries.当敌手A1发送(ida,idb,i,m)作代理签名询问时,C所作回应为: ① 如果idb并非第l次委派询问,C在列表L5中查找(ida,idb,i,m),并将其对应的(ui,vi)作为代理签名发送给敌手A1. ② 如果idb刚好是第l次委派询问,当i* 6) BreakinQueries.当敌手A1发送(idb,j)作密钥更新询问时,C所作回应为: ① 如果idb并非第l次委派询问,C在列表L4中查找(Ta→b|j,Tb|j),并将其作为此时的签名私钥发送给敌手A1. ② 如果idb为第l次委派询问且j=i*,C终止计算. 1) 1≤t* 证毕. 引理8.假定格上的SIS问题在多项式时间算法攻击下是困难的,则以上格上的前向安全代理签名方案在类型2敌手攻击下是存在性不可伪造的. 调用:调用格上的SIS问题实例,模拟器C需要返还一个合法的解. 首先,我们假设3个条件成立: 1) 对于每一个时间周期i=0,1,…,T-1,敌手A2可以适应性地对任意身份作多项式次H询问; 2) 对于任意的j 3) 在对任意签名人作签名私钥询问之前,假定A2已经预先完成相关的H和H1询问. Queries.当敌手A2伪造签名时,假设C随机选择i*(1≤i*≤T-1)作为伪造签名的时段.敌手A2可以适应性地作询问. 1)H-Oracle-Query.对于任意的时间i=0,1,…,T-1,A2可以适应性地对任意身份作H询问. 模拟者C维持一个列表L6={ida,idb,i,Ri}.输入身份和时间的一组数据(ida,idb,i),C首先在列表L6中查找(ida,idb,i).若(ida,idb,i)已存在在L6中,则模拟者C返还相应的Ri给敌手A2.否则,C从Dm×m中选择一个矩阵Ri并存储(ida,idb,i,Ri)在列表L6中.最后,模拟者C返还相应的Ri给敌手A2. 2) DelegateQuery.模拟者C维持一个列表L8={ida,idb,0,Ta→b|0}.假定Q表示敌手能够做的委派询问的最大次数,敌手A2随机选择l∈{1,2,…,Q},C所作回应如下: 如果idb并非第l次委派询问,则C回应为:输入身份和时间列表(ida,idb,0),C首先查找列表L6找到其对应的Hash值R0并运行BasisDel(A,R0,TA,σ0)生成Ta→b|0.最后,模拟者C将(ida,idb,0,Ta→b|0)存储在列表L8中,并将Ta→b|0发送给A2. 如果idb刚好是第l次委派询问,则C终止操作. 3) KeyUpdateQueries.C维持列表L9={ida,idb,i,Aa→b|i,Ta→b|i,Bb|i,Tb|i}.当敌手A2发送(ida,idb,i)作签名私钥询问时,C所作回应如下. 如果idb刚好是第l次委派询问,则C回应为: ③ 如果i*+1 4)H1-Oracle-Queries.C维持列表L10={ida,idb,i,m,ui,vi,Bb|ivi}.当敌手A2发送(ida,idb,i,m)作H1询问时,C所作回应为:如果L10列表中已经存在(ida,idb,i,m),则将其对应的Bb|ivi作为其Hash值H1(ida|idb|m|i)发送敌手;否则,C在列表L6,L7和L9中分别查找H(ida|idb|i),H(idb|i))和(ida|idb,i,Aa→b|i,Ta→b|i,Bb|i),然后模拟者采样可得vi←SampleDom(1n)并计算Bb|ivi.由于敌手A2知道TA,在做完H询问后敌手A2可知Ta→b|i,然后计算ui←SamplePre(Aa→b|i,Ta→b|i,Bb|i,si),并将数据(ida,idb,i,m,ui,vi,Bb|ivi)存储于列表L10中. 5) ProxySignQueries.当敌手A2发送(ida,idb,i,m)作代理签名询问时,C所作回应为: ① 如果idb并非第l次委派询问,C在列表L10中查找(ida,idb,i,m),并将其对应的(ui,vi)作为代理签名发送给敌手A2. ② 如果idb刚好是第l次委派询问,当i* 6) BreakinQueries.当敌手A2发送(idb,j)作密钥更新询问时,C所作回应为: ① 如果idb并非第l次委派询问,C在列表L9中查找(Ta→b|j,Tb|j),并将其作为此时的签名私钥发送给敌手A2; ② 如果idb为第l次委派询问且j=i*,C终止计算. 1) 1≤t* 证毕. 由引理7和引理8可知,定理2必然成立.故而3.1节构造的前向安全的格基代理签名在随机预言机模型下是不可伪造的,且是前向安全的. 由表1容易看出,文献[14-15]中方案的代理私钥长度和代理签名长度明显比其他方案的相应长度短.这是由于采用了抛弃采样技术而非原像采样技术,而抛弃采样技术是提高格基签名效率的主要应用手段.本文提出的代理签名方案由于要实现前向安全性,故而采用了格基委派技术和原像采样算法技术(而非抛弃采样技术,若采用抛弃采样技术则无法逐级实现密钥更新),因而,相较于文献[13],私钥及签名长度会随着分级i增大而增加. Table 1 The Efficiency Comparison of Different Schemes in Random Model 定理3.以上格基前向安全代理签名满足正确性. 证明. 假设(ui,vi)为消息m的签名,由ProxySign可知向量ui←SamplePre(Aa→b|i,Ta→b|i,si,μ)以及vi←SamplePre(Bb|i,Tb|i,si,μ).由引理3可知ui和vi分别服从分布DΛμ(Aa→b|i),si和DΛμ(Bb|i),si.因而可得Aa→b|iui=μmodq,Bb|iui=μmodq.由KeyUpdate以及引理6可知: 证毕. 定理4.假定格上的SIS问题在多项式时间算法攻击下是困难的,则以上格上的前向安全代理签名方案在标准模型下是存在性不可伪造的. 引理9.假定格上的SIS问题在多项式时间算法攻击下是困难的,则以上格上的前向安全代理签名方案在类型1敌手攻击下是存在性不可伪造的. 调用:调用格上的SIS问题实例,模拟器C需要返还一个合法的解. 5) 运行SampleRwithBasis(Ai,j),生成1个矩阵R~Dm×m以及格Λ⊥(Ai,jR-1)的1个小范数基T. Queries.当敌手A1伪造签名时,假设C随机选择i*(1≤i*≤T-1)作为伪造签名的时段.敌手A1可以适应性地作询问. 1) DelegateQuery.模拟者C维持一个列表L2={ida,idb,0,Ta→b|0}.假定Q表示敌手能够做的委派询问的最大次数,敌手A1随机选择l∈{1,2,…,Q},C所作回应为: 如果idb并非第l次委派询问,挑战者C执行如下: ④ 挑战者C将(ida,idb,0,Ta→b|0)存储至列表L2中,并将Ta→b|0返还给敌手A1. 如果idb刚好是第l次委派询问,则C终止操作. 2) KeyUpdateQueries.C维持列表L3={ida,idb,i,Aa→b|i,Ta→b|i,Bb|i,Tb|i}.当敌手A1发送(ida,idb,i)作签名私钥询问时,C所作回应如下. 如果idb并非第l次委派询问,则C回应为: ④ C将(ida,idb,i,Aa→b|i,Ta→b|i,Bb|i,Tb|i)存储至L3中,并将Ta→b|i和Tb|i返还给敌手. 如果idb刚好是第l次委派询问,则C回应为: ③ 如果i*+1 3) ProxySignQueries.挑战者C维持一个列表L4=(ida,idb,i,m,ui,vi).当敌手A1发送(ida,idb,i,m)作代理签名询问时,C作询问应答: ② 如果idb刚好是第l次委派询问,挑战者C执行为: Ⅱ.如果i*≤i 4) BreakinQueries.当敌手A1发送(idb,j)作密钥更新询问时,C所作回应为:如果idb并非第l次委派询问,C在列表L3中查找(Ta→b|j,Tb|j),并将其作为此时的签名私钥发送给敌手A1;如果idb为第l次委派询问且j=i*,C终止计算. 1) 1≤t* 证毕. 引理10.假定格上的SIS问题在多项式时间算法攻击下是困难的,则以上格上的前向安全代理签名方案在类型2敌手攻击下是存在性不可伪造的. 调用:调用格上的SIS问题实例,模拟器C需要返还一个合法的解. 5) 运行SampleRwithBasis(Bi,j),生成一个矩阵R~Dm×m以及格Λ⊥(Bi,jR-1)的一个小范数基T. Queries.当敌手A2伪造签名时,假设C随机选择i*(1≤i*≤T-1)作为伪造签名的时段.敌手A2可以适应性地作询问. 1) DelegateQuery.模拟者C维持一个列表L2={ida,idb,0,Ta→b|0}.假定Q表示敌手能够做的委派询问的最大次数,敌手A2随机选择l∈{1,2,…,Q},C所作回应: 如果idb并非第l次委派询问,挑战者C执行如下. ③ 挑战者C将(ida,idb,0,Ta→b|0)存储至列表L2中,并将Ta→b|0返还给敌手A2. 如果idb刚好是第l次委派询问,则C终止操作. 2) KeyUpdateQueries.C维持列表L3={ida,idbi,Aa→b|i,Ta→b|i,Bb|i,Tb|i}.当敌手A1发送(ida,idb,i)作签名私钥询问时,C所作回应. 如果idb并非第l次委派询问,则C回应. ④ C将(ida,idb,i,Aa→b|i,Ta→b|i,Bb|i,Tb|i)存储至L3中,并将Ta→b|i和Tb|i返还给敌手. 如果idb刚好是第l次委派询问,则C回应: ③ 如果i*+1 3) ProxySignQueries.挑战者C维持1个列表L4=(ida,idb,i,m,ui,vi).当敌手A1发送(ida,idb,i,m)作代理签名询问时,C按照如下方式作询问应答: 如果idb并非第l次委派询问,挑战者C执行如下: ① C首先在列表L3中查找其对应的(Ta→b|i,Tb|i). 如果idb刚好是第l次委派询问,挑战者C执行为: ② 如果i*≤i 4) BreakinQueries.当敌手A1发送(idb,j)作密钥更新询问时,C所作回应如下:如果idb并非第l次委派询问,C在列表L3中查找(Ta→b|j,Tb|j),并将其作为此时的签名私钥发送给敌手A1;如果idb为第l次委派询问且j=i*,C终止计算. 1) 1≤t* 证毕. 由引理9和引理10可知,定理4必然成立.故而4.1节构造的前向安全的格基代理签名在标准模型下满足不可伪造性和前向安全性. 鉴于其众多的应用场景,前向安全代理签名自提出以来就受到了广泛的关注.然而,随着量子计算机的出现,基于传统数论问题——大整数分解和离散对数的前向安全代理签名方案在量子计算环境下已不再安全.因此,如何构造量子免疫的前向安全代理签名是后量子时代迫切需要解决的问题. 由于具备量子免疫性,计算简单高效,任意实例下的安全性和最坏实例下的安全性相当等诸多优势,格公钥密码成为后量子时代公钥密码的最佳选择.本文基于格基困难问题——SIS问题提出了2个前向安全代理签名方案.第1个签名方案是在随机预言机模型中被证明是不可伪造的;第2个签名方案则是在标准模型中被证明是安全的.为了进一步丰富格基签名的应用场景,在后续的工作中,我们将逐步关注具有特殊性质的前向安全代理签名,构造格上安全的前向安全盲代理签名、前向安全多级代理签名,将成为我们今后的工作重心.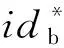
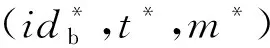
3 随机预言机模型下格基前向安全代理签名
3.1 方案描述
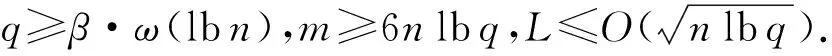
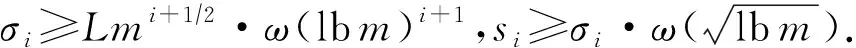

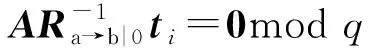

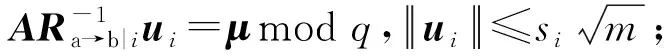
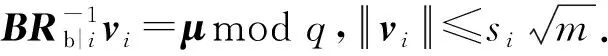
3.2 正确性
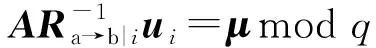
3.3 安全性分析


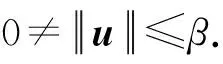


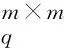
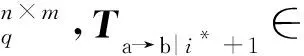
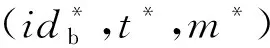


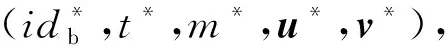





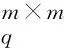
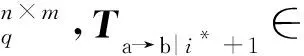
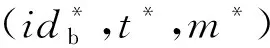


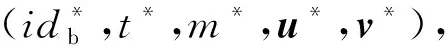
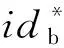
3.4 效率分析
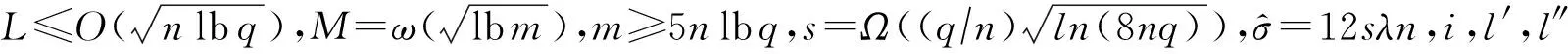

4 标准模型下格基前向安全代理签名
4.1 方案描述

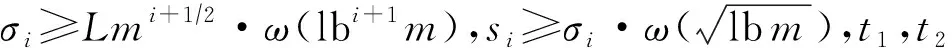

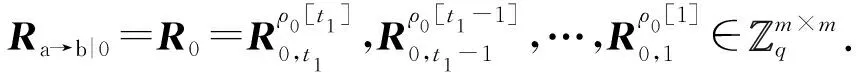
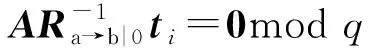

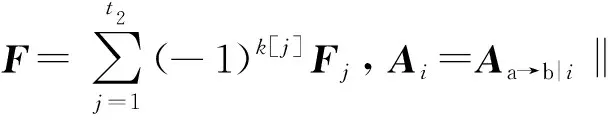

4.2 正确性
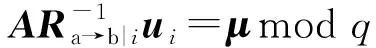
4.3 安全性分析


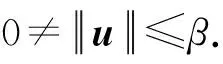
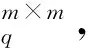
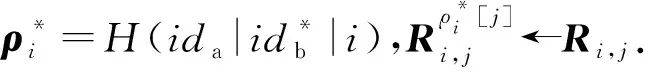


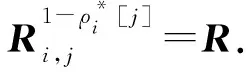
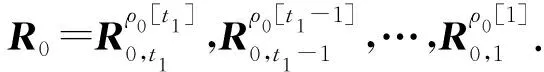

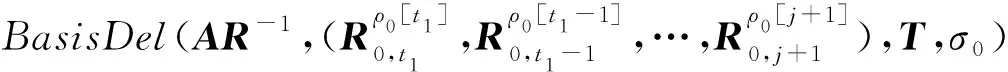

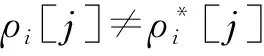
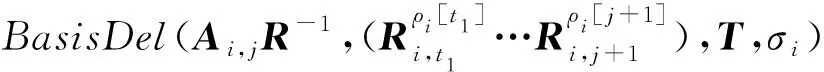
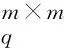
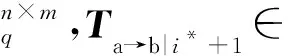
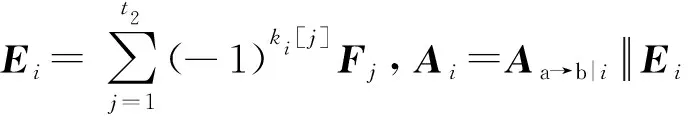





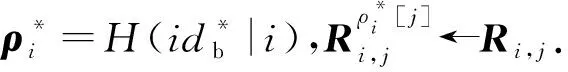
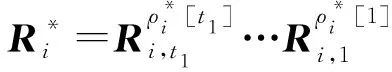
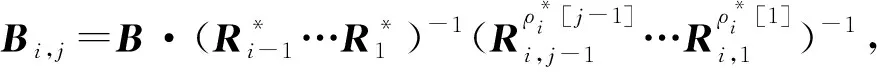
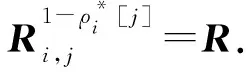
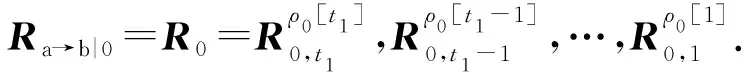
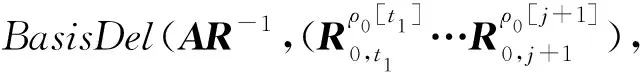

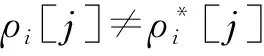
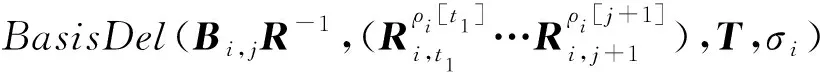


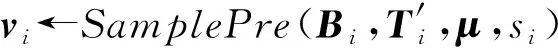



5 总 结

