慢前沿冲击电流与放电通道光强度关系研究

周蜜， 范雅蓓， 王建国， 卢泳茵， 蔡力， 樊亚东

(武汉大学 电气与自动化学院，武汉 430072)

0 引 言

雷电流是雷电物理研究与雷电防护领域十分重要的基础参数[1]。自然闪电发生具有时空随机性和瞬时性的特点，直接测量自然闪电过程的放电电流较为困难，目前大多通过测量放电引起的地面电场变化对电流进行反演和估计，这种反演往往仅限于闪电回击电流部分，且获得的是峰值电流。

人工触发闪电以及在高塔上布置的自然闪电监测可以直接测量雷电流，但通常为闪电通道底部的电流信号，在研究闪电通道电流沿通道的变化等方面存在局限。与雷电过程相关、且相对较容易实现的通道光学观测研究进展表明，闪电通道光强度与流过的雷电流密切相关，研究放电电流与通道发光强度之间的关系，有助于掌握雷电通道光学及电流时空分布特征，对建立闪电通道计算模型[2-4]、揭示雷电通道电磁场辐射特性等[5-7]具有重要意义。

目前利用自然闪电观测[8-12]以及人工触发闪电手段[13-19]开展过雷电流与通道光强度关系研究，如采用帧率为500帧/秒量级的高速摄像系统，Diendorfer等[8]在奥地利Gaisberg塔上行闪电的初始电流阶段发现电流和通道亮度线性相关；在巴西西南部及南部地区，Campos等[9-11]采用了帧率1000帧/秒的高速摄像机获得光学信号，研究自然闪电中连续电流和M分量的波形特征；Flache等[12]则根据发光强度大小推断了闪电通道各分支电流大小；Qie等[13]还通过通道亮度数据估计回击前的连续电流幅值。

高电压实验室内可以产生不同波形特征的冲击电流波形[20-28]。Flowers[23]同步测量了实验室火花放电通道中的放电电流与相应通道发光强度，发现随着放电电流增大，通道发射光信号随之增大。Colvin等[24]在实验室中使用激光放电产生100 cm长的弧状等离子体通道观察发光通道，发现初始阶段光信号与电流之间存在关联性。Gomes 和Cooray[25]使用光电倍增管测量实验室250 mm和500 mm的长火花放电的通道亮度，发现光辐射与电流波形在上升阶段十分相似，0.5～3.5 kA范围内的电流幅度和光强度峰值具备线性关系。Bendjamin等[26]在实验室对2 mm和4 mm长度通道进行静电放电试验，发现在最初阶段光脉冲和电流波形的发展存在紧密联系。Lu等[27]还发现光强峰值随放电通道光强探测系统机械狭缝宽度增加而线性增加，但光强波形特征基本不变。Mitchard等[28]在实验室一对半球形钨电极之间产生冲击电流，发现实验室空气间隙击穿产生的雷电流电弧光谱与自然界闪电光谱非常类似，进一步表明了实验室电弧放电在雷电电流与通道光强度关系研究方面的潜在应用。

本文在高电压实验室内利用冲击电流发生器产生具有慢上升前沿的衰减振荡波形，同步测量石墨棒状放电间隙通道电流与光强度波形，计算电流波形和光强波形的峰值、10%～90%上升时间和半峰宽度等特征参数，并进一步分析这些参数在2种信号间的相关性。

1 试验布置与数据概况

在高电压实验室内利用冲击电流发生器产生阻尼正弦振荡电流波形，图1为实验装置示意图，放电电流流经石墨棒状间隙，放电间隙距离为15.0 mm。为消除环境光的影响，实验在相对黑暗的房间进行，放电间隙的背景为黑色遮光布包围。

图1 试验装置示意图Fig.1 Schematic diagram of experiment setup

采用输出灵敏度为0.001 V/A的Pearson电流探头测量放电通道电流，电流探头带宽1 Hz～1.2 MHz。利用一套放电通道光强度探测系统测量石墨棒状放电间隙的光强波形。通道光强度探测系统距离该放电间隙70 cm且其狭缝中心对准于间隙中心。该光强度探测系统由光电二极管模块、延长套管和可调狭缝组成。光电二极管模块是一种P-N结型的光检测二极管，利用了载流子的雪崩倍增效应放大光电信号以提高检测的灵敏度。图2为光电二极管模块的光谱响应曲线，光谱范围为200～1 000 nm，包含可见光光谱，在600 nm处具有峰值响应。为获得高信噪比的光强波形，使用HBM ISOBE5500光纤隔离系统。采用MDO 3024数字存储示波器同步记录输出的电流和光信号。更详细的试验布置可参考文献[27]。

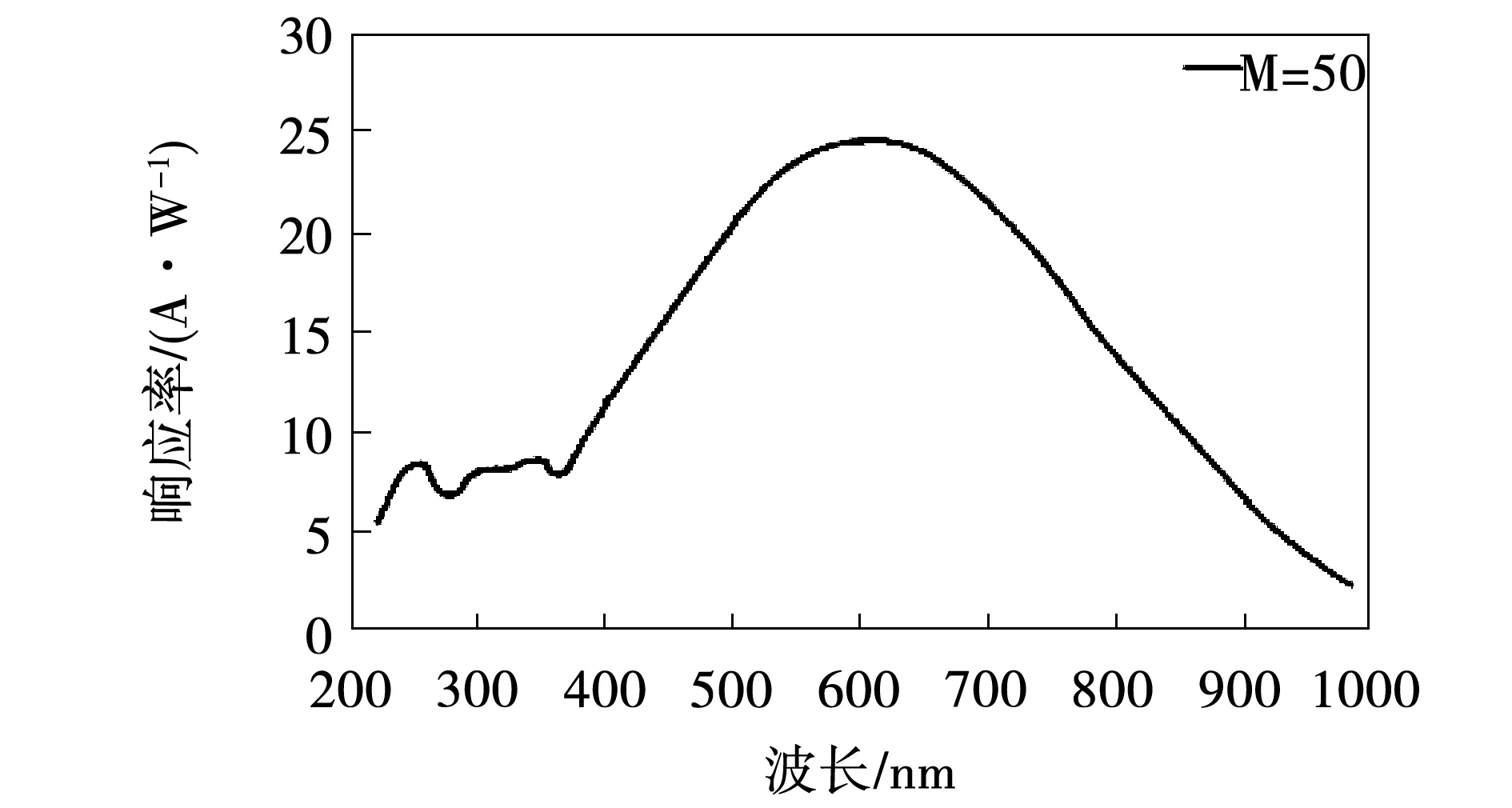
图2 光电二极管的光谱响应曲线Fig.2. Spectral responsivity of photodiode module

本文所产生的冲击电流为阻尼正弦振荡电流波形，表1为电路配置和波形参数，在25～40 kV范围内改变冲击电流发生器的充电电压，产生不同幅度的冲击电流波形。以电流波形首次脉冲的10%～90%上升时间和半峰宽度计算电流波形参数。例如，10.5/23.6 μs表示首次脉冲电流的10%～90%上升时间是10.5 μs，半峰宽度是23.6 μs。试验包括4组冲击电流共67个对称脉冲，含17个首次脉冲和50个在首次脉冲之后发生的后续脉冲，其峰值1.9～27.0 kA，10%～90%上升时间3.3～18.8 μs，半峰宽度7.8～47.8 μs，电流波形在上升和下降过程均呈现基于时间轴基本对称的特征。

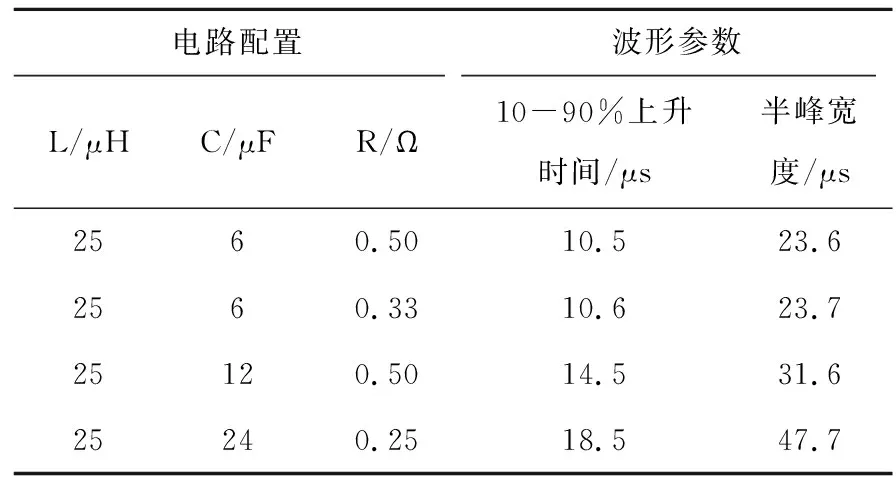
表1 不同电路的电流波形参数Table 1 Current waveform parameters for different circuits

图3是4组同步测量的电流波形及对应的光强波形，4组波形示例给出了不同电路配置下的测量结果。如前所述，通过改变电容器组的充电电压可以调节电流幅值，这种调整不会影响电流波形特征，与之对应的通道光强度信号波形也仅发生幅值上的变化，波形特征同样不变。由于光强波形的幅度无负极性数值，为更好地比较2种信号，将图3左侧电流波形原始值转化为右侧所示绝对值。冲击电流波形和光强波形均具有多个基本对称的脉冲。对2种信号的峰值、10%～90%上升时间、半峰宽度和电流转移电荷量等参数进行相关分析。

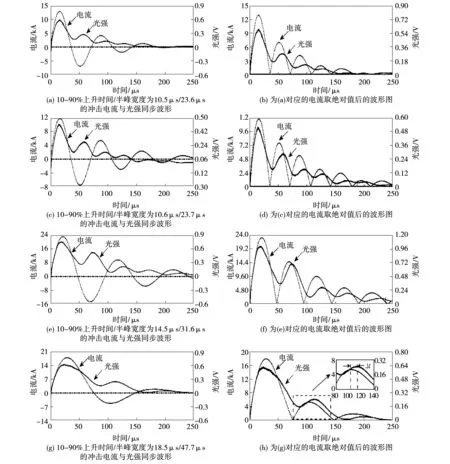
图3 冲击电流与光强同步波形Fig.3 Synchronous waveforms of impulse current and luminosity

2 电流与光强度波形特征参数分析

2.1 峰值

图4为17个首次脉冲的电流峰值和光强峰值拟合结果，包含了表1中4组电路配置下不同输出电流幅值下的所有同步数据。首次脉冲的电流峰值与光强峰值呈线性关系，线性回归的相关系数为0.93。图5为4组波形各自的脉冲电流峰值与光强峰值散点分布特征及拟合回归线，各组波形同时包含首次脉冲和后续脉冲，其脉冲电流峰值与光强峰值均线性相关。随着电流10%～90%上升时间增大，对应的回归线斜率有减小的趋势。

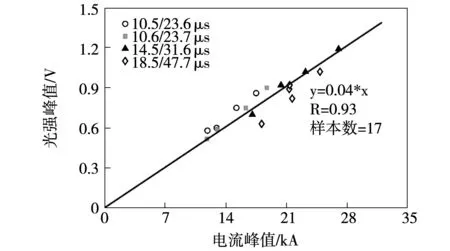
图4 首次脉冲电流峰值与光强峰值Fig.4 Current peak versus luminosity peak for the primary pulses

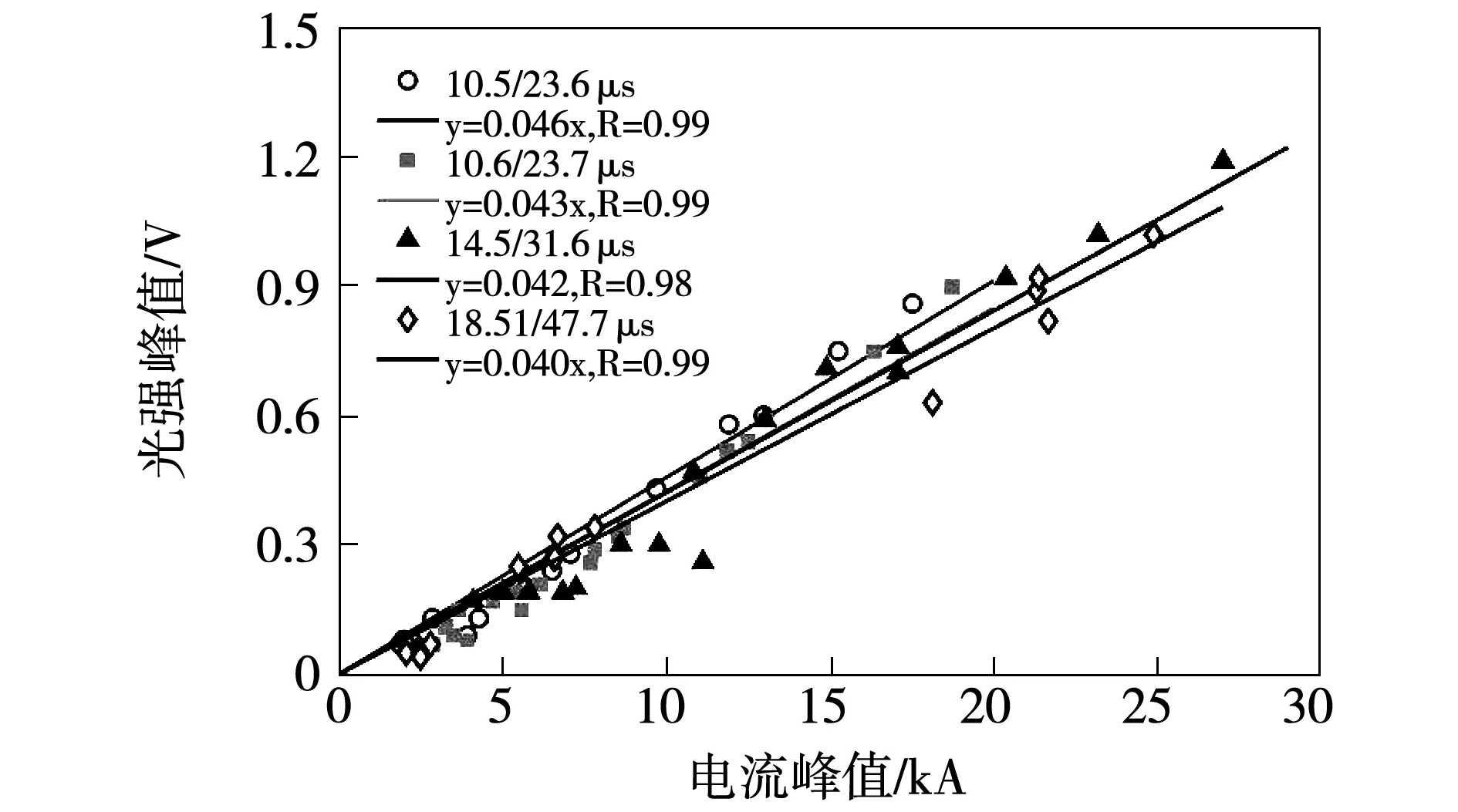
图5 单个波形电流峰值与光强峰值Fig.5 Current peak versus luminosity peak for the individual waveforms

图6呈现了4组波形总体的脉冲电流峰值与光强峰值拟合结果，相关系数为0.98，二者之间仍然具有很好的线性关系。比较图4和图6，首次脉冲和后续脉冲的电流峰值和光强峰值拟合表达式斜率相等，二者之间关系遵循相同的规律。

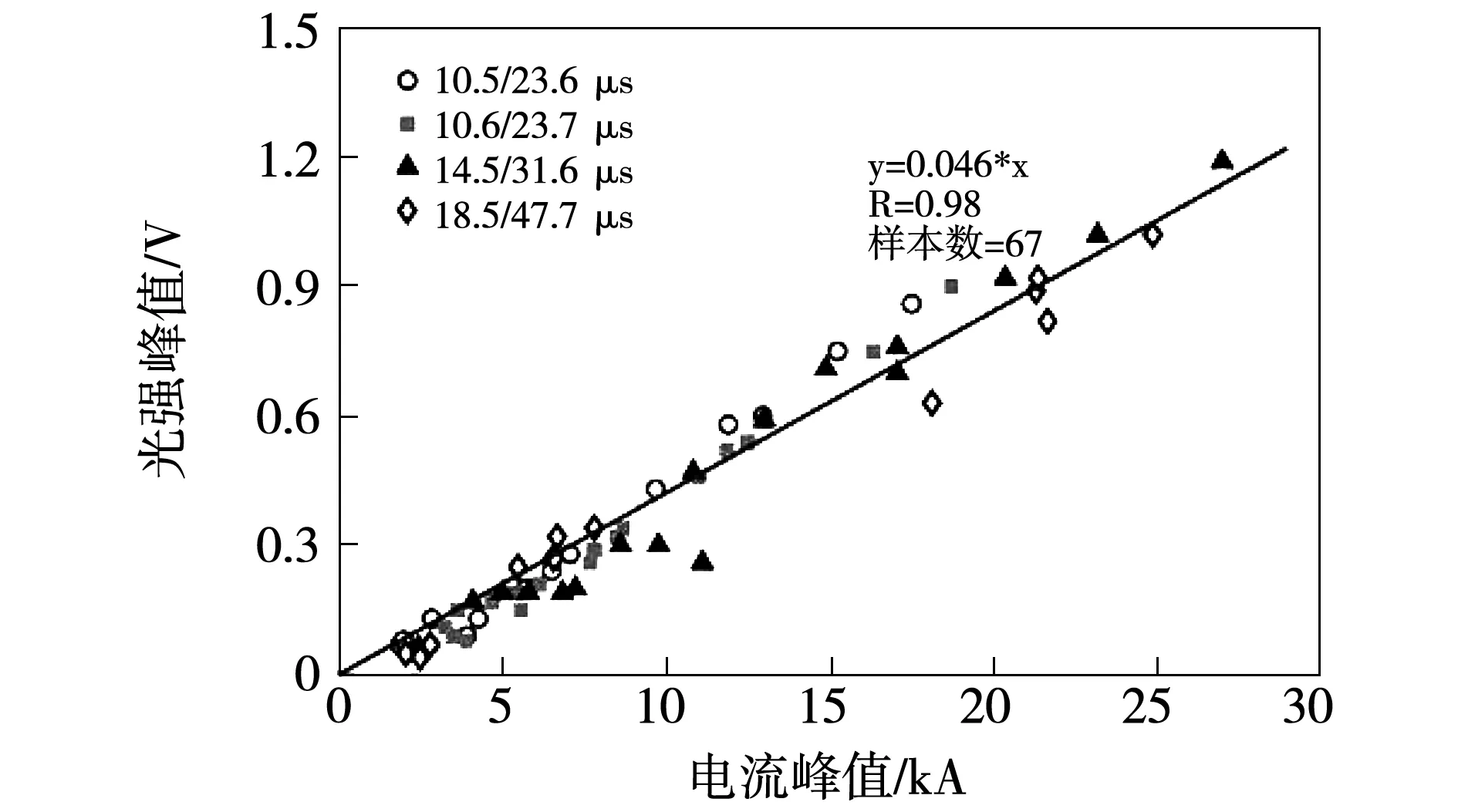
图6 所有脉冲电流峰值与光强峰值Fig.6 Current peak versus luminosity peak for all the data

2.2 10-90%上升时间

图7为首次脉冲电流10%～90%上升时间与光强10%～90%上升时间的关系，二者线性相关且相关系数为0.95。拟合表达式为y=0.83x，其中y表示光强10%～90%上升时间，x表示电流10%～90%上升时间。对于首次脉冲，电流10%～90%上升时间比对应光强10-90%上升时间长17%。

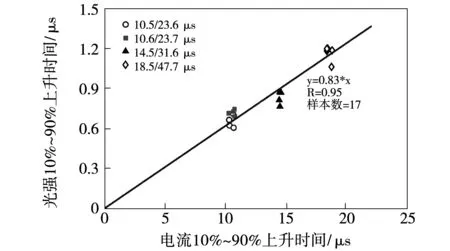
图7 首次脉冲电流10%～90%上升时间与光强10%～90%上升时间Fig.7 Current 10%～90% risetime versus luminosity 10%～90% risetime for the primary pulses

对所有脉冲电流10%～90%上升时间与光强10%～90%上升时间的散点进行线性拟合，结果如图8所示。线性回归线的相关系数为0.71，光强10%～90%上升时间与电流10%～90%上升时间之间存在大致的线性关系。与首次脉冲的光强波形相比，后续脉冲的光强波形在上升部分能更好地跟随电流波形。整体上，脉冲的光强10%～90%上升时间与电流10%～90%上升时间相对接近。

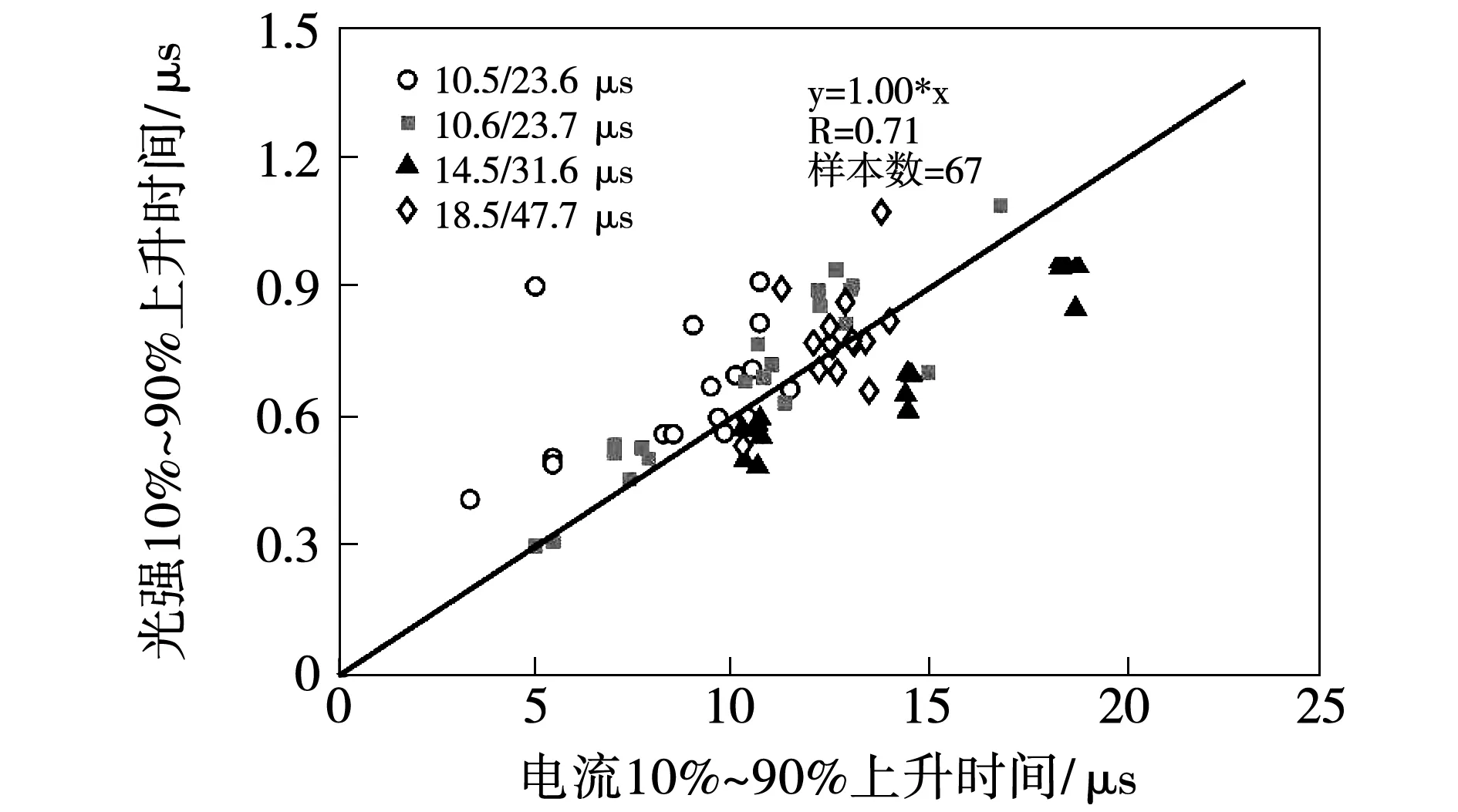
图8 所有脉冲电流10%～90%上升时间与光强10%～90%上升时间Fig.8 Current 10%～90% risetime versus luminosity 10%～90% risetime for all the data

2.3 半峰宽度

图9为首次脉冲电流半峰宽度与光强半峰宽度的拟合结果，二者也呈线性关系。由于回归线斜率为1.17，首次脉冲的光强半峰宽度比电流半峰宽度长17%左右。

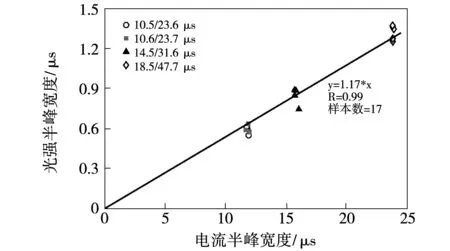
图9 首次脉冲电流半峰宽度与光强半峰宽度Fig.9 Current half-peak width versus luminosity half-peak width for the primary pulses

所有脉冲电流半峰宽度与光强半峰宽度的拟合结果如图10所示，相关系数为0.92，对于不同波形，电流半峰宽度与光强半峰宽度具有很好的线性相关性。线性拟合表达式y=0.94x表明光强半峰宽度比相应电流半峰宽度短6%左右。对比图7～图10的斜率，在上升阶段和下降阶段，相比首次脉冲，后续脉冲的光强波形与电流波形之间具有更好的跟随性。

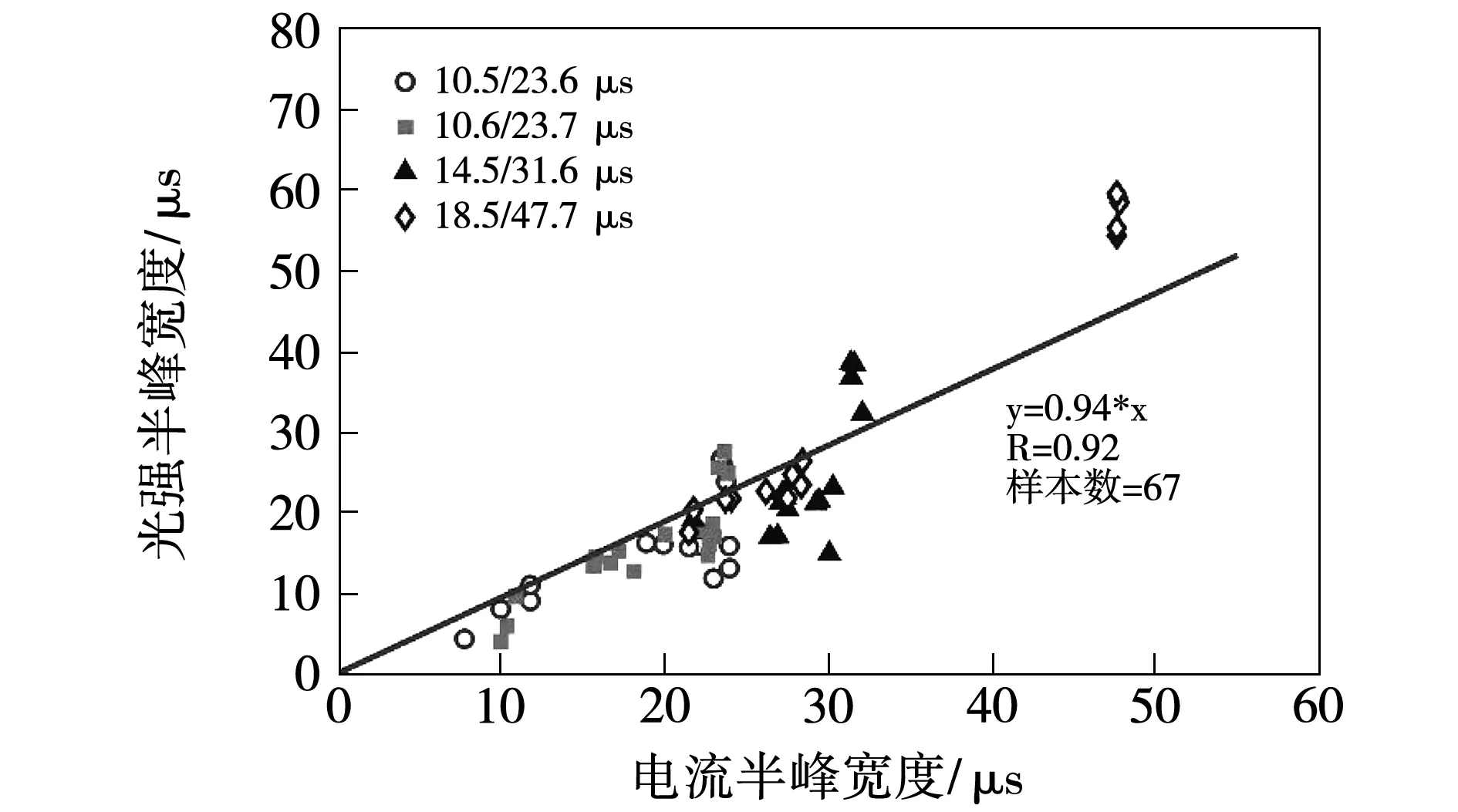
图10 所有脉冲电流半峰宽度与光强半峰宽度Fig.10 Current half-peak width versus luminosity half-peak width for all the data

2.4 转移电荷量

本文计算的电流转移电荷量q是电流波形绝对值相对于时间的积分，表达式为

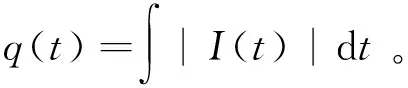
(1)

物理量上，电流转移电荷量与光辐射强度对时间积分相对应。图11为电流转移电荷量随光强对时间积分变化的散点图。图11结果表明，电流转移电荷量与光强—时间积分呈现较强的线性关系，相关系数为0.99。

图11 电流转移电荷量随光强-时间积分变化Fig.11 Current charge transfer versus luminosity-time integration

3 讨 论

本文在高电压实验室内产生了具有慢上升前沿的阻尼正弦振荡冲击电流波形，同步测量了冲击电流和放电通道光强波形。结果发现，对于实验室产生的慢前沿冲击电流波形，电流峰值与对应光强峰值之间有较强的线性相关性，二者的10%～90%上升时间与半峰宽度之间也存在线性关系。Zhou等[18]发现，人工触发闪电M分量电流与光强之间大致线性相关。Carvalho等[15]也报道了在人工触发闪电的回击和M分量中，电流10%～90%上升时间与光强10%～90%上升时间近似呈线性关系。就电流与对应通道光强度关系而言，本文结果与在人工触发闪电M分量过程中发现的两者关系结果十分相似。

在闪电连续电流和叠加M分量阶段通常会产生相对较大的电荷转移，与之相关的热效应是产生重大雷电损害的原因，如造成被雷击金属结构的过热损伤、架空输电线路的损坏以及森林火灾等[29]。Miki等[30]曾通过高速摄像拍摄得到的光学照片推算雷电流持续时间，并根据统计得到的连续电流平均电流值200 A估算了自然闪电中长连续电流(持续时间大于40 ms的连续电流)的转移电荷量。Miki等[30]的这种估算只包含了电流持续时间因素，忽略了波形变化。本文图11中关于电流转移电荷量随光强对时间积分变化间的相关性联系，既包含了时间因素，也包含了波形特征，2种参数间具有的强线性关系表明光学手段预测闪电转移电荷量的可行性。

如图3所示，当电流处于零点时，放电通道仍能观测到光信号，即零电流对应非零光强度。Liyanage等[31]测量了静电放电电流波形和光强波形，发现波长分别为559、778和821 nm的光强波形比对应的电流波形具有更广的信号范围。Visacro等[32]观察自然闪电放电电流和光强波形，也发现当电流减小到零时，闪电通道的光强度大于零。Walker等[33]观测闪电电流与同步高速光谱，发现在放电过程的冷却阶段中含有持续发光时间较长的中性氧、氮和氢原子，这些持续发光时间较长的中性原子，可能导致放电通道在电流为零时仍发光。出现这种现象的原因与放电通道电流对通道的加热效应有关。图3中电流即使瞬间过零，但通道温度未随电流过零而迅速冷却，以致在电流过零时刻通道依然发光，过零后电流幅值又开始增加，电流对通道的加热效应导致放电通道温度继续升高，因此通道光强度在未过零的情况下继续增大。

在图3所示的一次完整电流波形中，后续脉冲的光强波形明显滞后于对应的电流波形。为更清楚地展示这一现象，图3(h)中详细定义了光强与电流间的时延(Δt)。在闪电放电过程中，高温闪电通道中气体短时间内被加热到等离子态，热辐射产生的光谱是连续谱，含波长较长的可见光。同时，闪电电流使放电通道内的温度增加，气体分子或原子由于热激励从较低能级被激发到高能级，产生光辐射信号。无论是闪电电流在雷电通道中热辐射产生的可见光，还是雷电流使得气体分子或原子被激发到高能级发生跃迁产生的辐射光，都可能造成光辐射信号滞后于电流信号的现象。

Liang等[34]使用气体动力学模型计算闪电回击电流与对应光辐射信号之间延时，上升时间为1 μs的回击电流，辐射光信号延迟电流信号2 μs左右。Carvalho等[15]在人工触发闪电实测数据中证实了闪电回击阶段这种时延的存在，闪电回击光辐射强度滞后于电流波形的延时时间为数十到数百ns级，并大致随电流上升时间的增加而增加。Zhou等[18]发现在人工触发闪电初始连续电流脉冲和M分量中，也存在几十μs到几百μs的时延，这种时延随电流峰值的增大而减小。与电流波形参数密切相关的延时时间，将进一步影响回击电流发展速度的实际变化规律[35]。图12(a)和图12(b)分别为本实验中后续脉冲的时延随电流10%～90%上升时间和电流峰值变化的关系图，该时延随电流10%～90%上升时间增加而增大，与电流峰值之间无明显相关性。

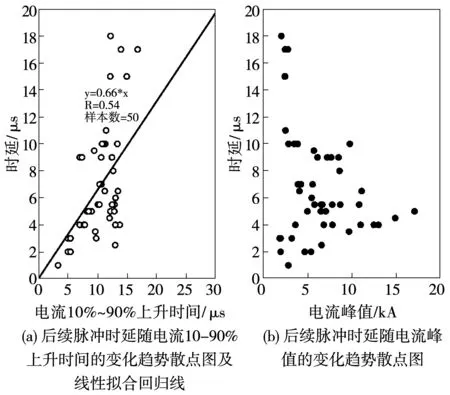
图12 后续脉冲时延随(a)电流10%～90%上升时间和(b)电流峰值变化Fig.12 Time delay versus (a) current 10%～90% risetime and (b) current peak

图3首次脉冲中未发现光辐射信号相对于电流的时滞现象，随着电流脉冲上升沿时间的增大，甚至呈现电流稍滞后于光强的特征，这种现象与初始时段放电通道的膨胀有关。当电流刚开始流过放电通道时，载流通道被突然加热，其压强很大，通道将发生膨胀，但短期内无法与周围空气达到压力平衡，具体表现在上升阶段通道光强波形不能很好地跟随电流波形，以致首次脉冲的光强上升时间略小于对应的电流上升时间，前者约为后者83%(见图7)。这种光强波形上升时间短于对应电流波形上升时间的现象在快前沿波形中更加显著[36]。因此，随着电流脉冲上升沿时间的增大，光信号与电流信号上升时间的绝对值差异也会逐渐增加，即使光强度相对电流存在滞后，也会被2种波形的上升时间上的差异所掩盖，造成首次脉冲中电流峰值迟滞于光强峰值的现象。随着时间的增加，放电通道逐渐与周围空气达到压力平衡，后续脉冲中光强波形能更好地跟随电流波形，其上升时间逐渐接近于对应电流波形的上升时间(见图8)，此时光强相对电流的迟滞效应开始显现。

4 结 论

在高电压实验室内利用冲击电流发生器对15 mm石墨棒状放电间隙放电，产生了具有慢上升前沿的衰减振荡冲击电流波形，峰值1.9～27.0 kA，10%～90%上升时间3.3～18.8 μs，半峰宽度7.8～47.8 μs，进行了4组电流共67个脉冲，含17个首次脉冲及50个后续脉冲与通道光强度同步测量实验，开展了冲击电流与通道光强度特征参数关系研究。主要结论如下：

1)首次脉冲和后续脉冲的电流峰值与光强峰值均具有较强的线性关系。光强10%～90%上升时间与电流10%～90%上升时间大致线性相关，在电流半峰宽度与光强半峰宽度之间也存在线性关系。电流转移电荷量与光强-时间积分呈现明显的线性相关性；

2)相比首次脉冲，后续脉冲的光辐射强度波形在上升阶段及下降阶段均能更好地跟随电流波形。在后续脉冲中，光强脉冲滞后于对应电流脉冲。电流和光强同步波形的时延随电流10%～90%上升时间增加而增大；

3)就电流与对应通道光强度关系而言，高电压实验室产生的具有基本对称脉冲特征的冲击电流与人工触发闪电M分量电流脉冲性质相似。