黏性土坡上裙板式条形基础的极限承载力

赵志峰，方舟

(南京林业大学土木工程学院，南京 210037)

天然黏性土地基上浅基础的不排水极限承载力qu受到了Prandtl、Terzaghi、Meyerhof、Hansen等学者的重视，并给出了条形基础的计算公式：

qu=Nccu

(1)

式中：cu为黏性土不排水强度；Nc为承载力系数。各学者推导时采用的假定不尽相同，体现在承载力系数的计算上有所区别。

当基础位于坡上时，其极限承载力受到坡角、基础位置、黏聚力等因素的影响，相比平地时有所降低。目前，研究斜坡上浅基础承载力的文献成果不多，也缺少精确的理论解。

在基础下方设置裙板可有效约束基础板下土体的剪切变形，提高地基承载力[1]。裙板式浅基础在沿海工程中已经得到了成功的应用[2-4]。同样，对黏性土坡上的条形基础设置裙板也可提高其承载力，减少斜坡对承载力的不利影响。

关于裙板式基础在黏性土和砂土中的极限承载力，已有部分学者通过数值计算开展了相关研究[3-5]，得出承载力计算公式。而坡上裙板基础的承载力目前还缺乏相关研究。笔者以黏性土坡上裙板条形基础为研究对象，通过数值计算和理论分析确定其极限承载力，并分析坡角、不排水抗剪强度、基础位置等因素对承载力的影响。

1 数值模型的建立

1.1 材料参数

裙板式浅基础的示意图见图1。坡角为β,黏性土不排水抗剪强度为cu,饱和重度为γsat,变形模量为E。基础宽度为B,裙板长度为d,基础边缘距坡顶水平距离为λB。基础板和裙板材料为C30混凝土，厚度均取0.2 m，弹性模量为30 GPa。土体采用实体单元模拟，选用Mohr-Coulomb本构模型，基础采用线弹性材料模拟。基础板和裙板设置为粗糙、与土体刚性接触。

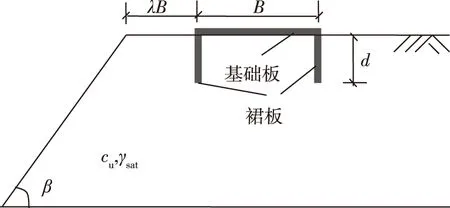
图1 坡上裙板式条形基础示意图Fig.1 Schematic diagram of skirted strip foundation on slope

采用位移加载的方式确定承载力，即在基础板上施加竖直向下的位移，位移大小为0.25B。根据计算结果可整理出基础中心点的p-s曲线，从而确定极限承载力pu。为提高计算精度，剖分网格时，对裙板基础周边区域的网格进行了加密。约束条件：模型底部施加完全约束，竖直边界施加水平约束。

1.2 模拟方案

根据前人的研究，影响黏性土坡上条形基础极限承载力的主要因素有：坡角β、相对距离λ、不排水强度cu、重度γsat、裙板相对高度d/B等。其中，基础宽度和重度的影响及变化范围较小，在模拟中设为常数：B=2 m、γsat=20 kN/m3。黏性土的变形模量参考国外学者取相对值的方法[6]，即E/cu=500；泊松比取0.5。数值分析中的主要变量为基础距坡顶相对距离λ、坡角β、强度cu和裙板相对高度d/B。各变量的取值如下：

1)β=15°，30°，45°；

2)cu=30，35，40，45，50，55，60，70，80，90 kPa；

3)λ=1，2，3；

4)d/B=0，0.5，1.0。

研究中进行单因素分析，即某个变量变化时其他参数保持不变，因此建立的数值模型数量较多，目的是对承载力的影响因素进行全面分析。

2 数值计算结果

2.1 计算结果的验证

为验证数值计算的可靠性，进行了平地上条形基础(B=2 m)的建模计算，并与承载力理论解进行了对比。对比的理论为Prandtl解和Terzaghi解。根据Prandtl理论，承载力系数Nc=π+2≈5.14，qu=5.14cu；根据Terzaghi理论，当φ=0时，Nc=3π/2≈5.7[7]，qu=5.7cu。将不同cu下数值计算结果同两种理论解进行对比，如图2所示。

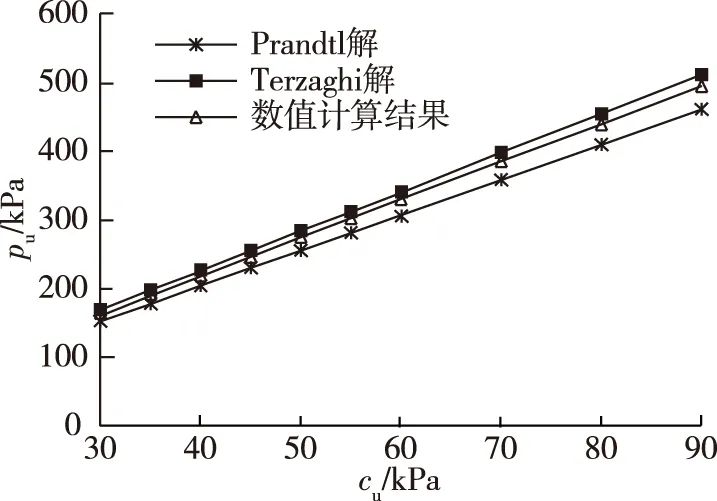
图2 极限承载力理论解与数值解对比Fig.2 Bearing capacity comparison between theoretical solution and numerical simulation

从图2可以看出，数值计算结果介于两种理论解之间，更接近Terzaghi解。由于Prandtl解是假定基础底面光滑，而Terzaghi解基于基底完全粗糙，所以Terzaghi解更接近实际。

2.2 裙板对承载力的影响

1)β=15°时。

β=15°，当基础与坡顶的距离达到1B(λ=1)时，未设置裙板(d/B=0)的承载力与平地接近，设置裙板后极限承载力有明显的提高，如图3a所示。λ=2时的结果与λ=1时接近，故不再赘述。当λ=3时，裙板相对高度d/B对承载力的提高有明显作用。

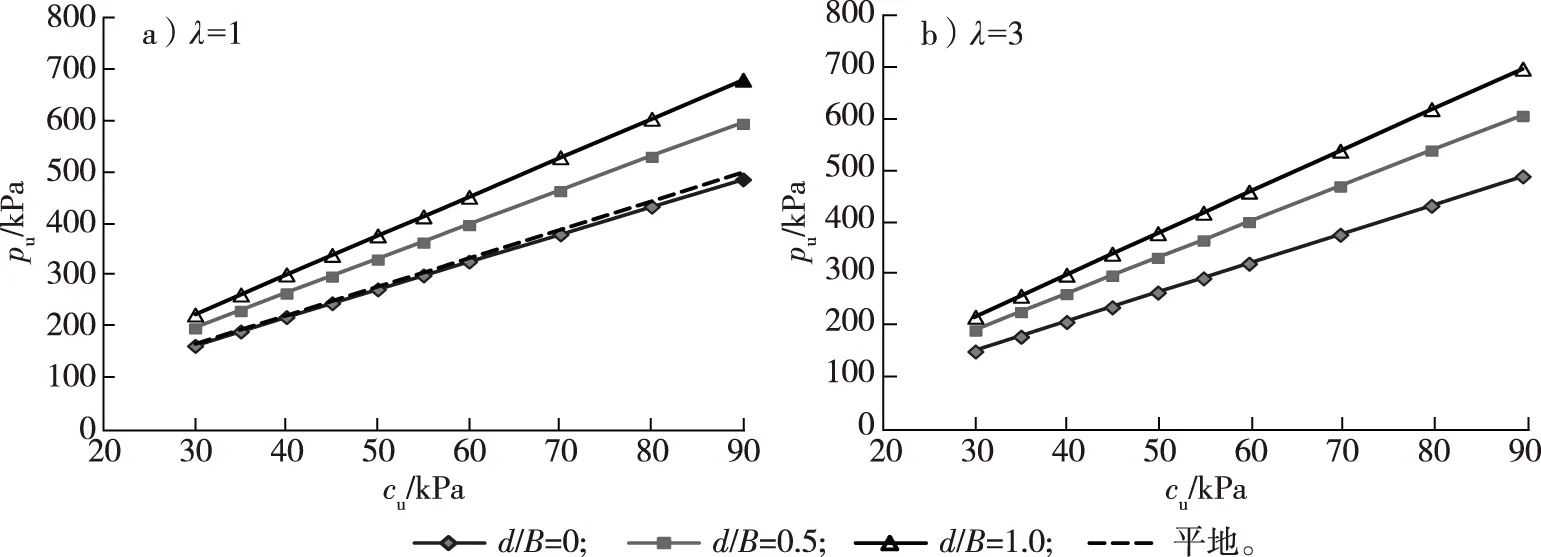
图3 β=15°时d/B对承载力的影响Fig.3 Influence of d/B to the bearing capacity at β=15°

为定量评价裙板相对高度对承载力的影响，将d/B=0.5和1.0与d/B=0(无裙板)进行比较。以λ=1为例，如图4所示，d/B=0.5时的承载力提高了21%～22%；d/B=1.0时的承载力提高了38%～40%。λ=2时，d/B=0.5时的增幅为23%～24%；d/B=1.0为40%～41%。

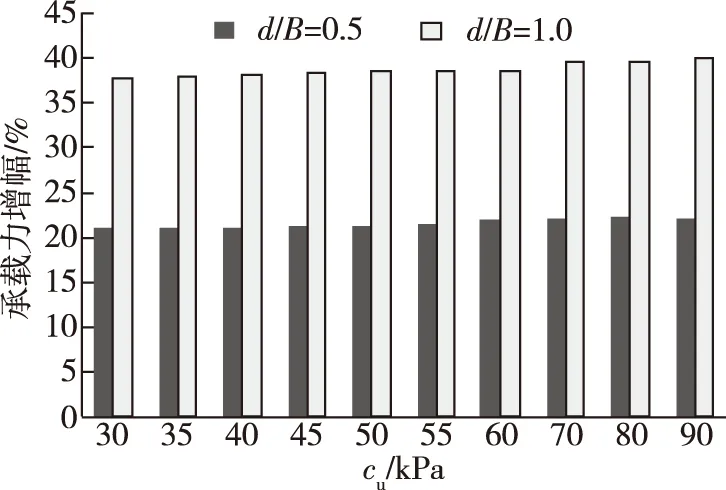
图4 β=15°、λ=1时不同d/B时承载力增幅Fig.4 Increment of bearing capacity with different d/B at β=15° and λ=1

2)β=30°时。

β=30°，当基础与坡顶的相对距离λ=1和λ=2时，d/B=0(无裙板)的承载力低于平地；d/B=0.5时的承载力有明显提高(图5)。

当λ=1、d/B=0.5时的承载力相比无裙板提高了约16%～18%，d/B=1.0时增加了30%～34%；λ=2、d/B=0.5时的承载力提高了20%～21%，d/B=1.0时增加了32%～37%。λ=3、d/B=0.5时的承载力提高了21%～22%，d/B=1.0 时增加了34%～38%。当cu较低时，承载力的增幅相对较小。

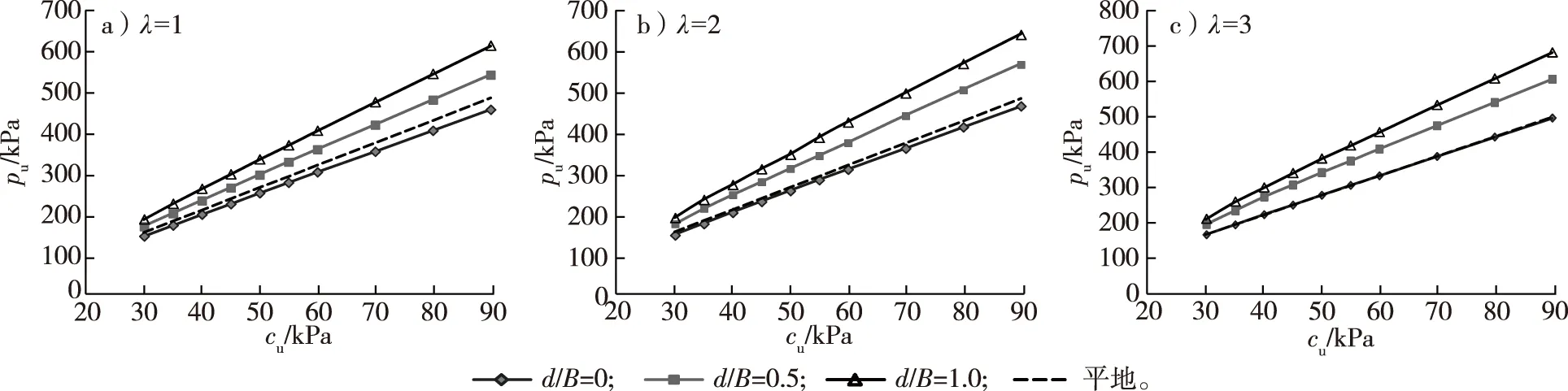
图5 β=30°时d/B对承载力的影响Fig.5 Influences of d/B on the bearing capacity at β=30°

3)β=45°时。

当λ=1时，d/B=0(无裙板)的承载力明显低于平地；d/B=0.5时承载力有明显提高，cu超过40 kPa后的承载力已接近平地(图6)。这说明坡角较大时，裙板对提高坡上基础承载力有显著作用。

当λ=2时，d/B=0的承载力低于平地；d/B=0.5和1.0时的承载力均超过平地。当λ=3时，d/B=0的承载力与平地比较接近，说明此时坡角对承载力的影响降低。

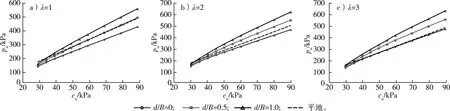
图6 β=45°时d/B对承载力的影响Fig.6 Influences of d/B on the bearing capacity at β=45°

2.3 相对距离的影响

当基础位于坡上时，基础与坡顶的相对距离λ对承载力有明显影响[8]，且这种影响与不排水强度cu相关。图7为不同cu时，d/B=0.5的裙板基础极限承载力。当cu=30 kPa时，λ对不同坡角的裙板基础承载力影响较小；当cu=60 kPa时，λ对15°坡上基础承载力的影响不大，但随着坡角增加至30°和45°，承载力随着λ的增大明显提高。

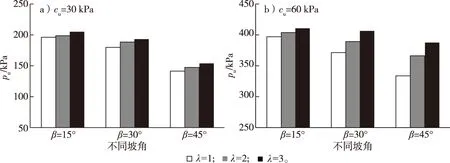
图7 相对距离对裙板基础承载力的影响Fig.7 Influences of slope angle on the bearing capacity of skirted footing at d/B=0.5

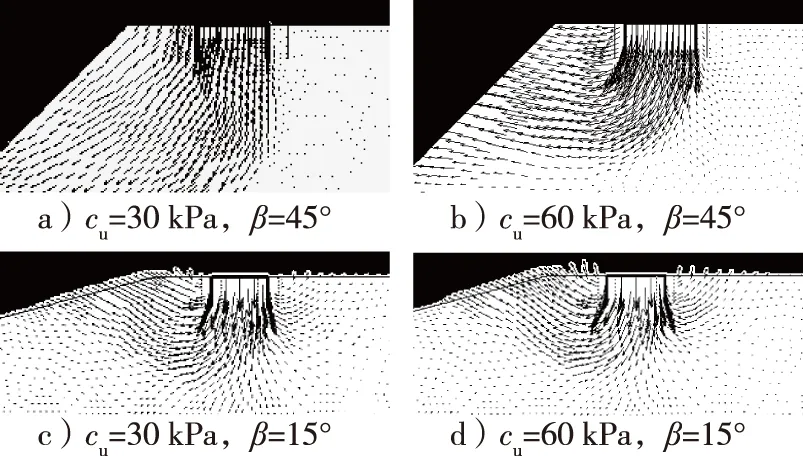
图8 λ=1时不同坡角时裙板基础的位移趋势Fig.8 Movement tendency of skirted footing with different slope angles at λ=1

黏性土坡的坡角及不排水强度会影响坡上基础的破坏模式，进而影响其承载力。已有研究指出，距坡顶较近时，基础在竖向荷载下的破坏模式受斜坡整体稳定的影响[9]；而当基础与坡顶距离增大到某个临界值后，斜坡的影响可忽略。从图8可以看出，当坡角为45°、λ=1时，裙板基础下方的地基土向坡面运动的趋势明显，表明地基承载力受斜坡影响，设置裙板的作用不明显；而cu较高时破坏面的范围较小。当坡角为15°时，地基土的破坏受斜坡的影响小，尤其是cu=60 kPa时，地基土的破坏趋势与平地相差不大。这也解释了λ对15°坡上基础的承载力影响较小，而当坡角为45°时，λ对承载力有显著影响。

2.4 坡角对承载力的影响

以d/B=0.5为例，当基础距坡顶较近时，坡角对裙板基础的承载力影响较大(图9)。当λ=1、β=45°时的承载力与平地接近，在cu较小时低于平地；当β=30°和15°时，承载力明显高于平地。λ=3时，裙板基础的承载力均超过平地。

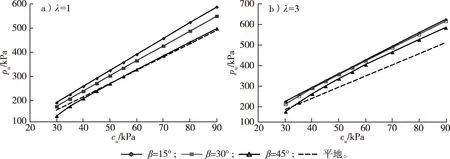
图9 坡角对裙板基础承载力的影响Fig.9 Influences of slope angle on the bearing capacity of skirted footing

3 承载力的理论计算

同平地上条形基础相比，黏性土坡上裙板式条形基础的极限承载力多了两个影响因素：斜坡和裙板。其中斜坡对承载力存在削弱作用，而裙板能提高承载力。因此在推导时，需要考虑这两方面对承载力的影响，极限承载力计算公式可表示为：

(2)

式中：ξ为斜坡引起的承载力折减系数；dc为裙板对承载力的提高系数；Nc为平地基础的承载力系数，则Nccu为其极限承载力,如公式(1)所示。

关于裙板基础的极限承载力，国外学者进行了相应研究，并给出了其承载力计算的公式：

pu=dc·Nccu

(3)

关于深度系数dc，根据大量的计算统计建议用公式(4)确定[9]：

dc=1+n(d/B)m

(4)

式中：n=0.2～0.4；m=0.4～0.6。系数n和m的取值可根据具体计算确定。例如，Yun等[9]建议对于正常固结黏性土：

dc=1+0.25(d/B)0.4

(5a)

Whitlow[10]给出的计算公式：

dc=1+0.235(d/B)0.5

(5b)

Salgado建议的深度系数确定公式：

dc=1+0.27(d/B)0.5

(5c)

根据本次模拟得到的结果，当裙板相对高度d/B=1.0且地基承载力受斜坡影响较小时，pu可提高30%以上，因此确定系数n=0.3。然后通过对d/B=0.5时承载力结果的分析，确定m=0.5。因此得到：

dc=1+0.3(d/B)0.5

(6)

根据之前的数值计算，黏性土坡上基础的承载力与坡角β、黏性土不排水强度cu、基础与坡顶的相对距离λ有关。Vesic给出此时的承载力系数：

(7)

公式(7)未考虑基础与坡顶距离对承载力的影响。Georgiadis通过数值计算研究了坡上条形基础的不排水承载力，给出了如下的计算公式[11]：

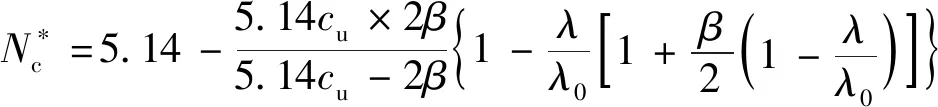
(8)

式中，λ0为临界距离，即超过这一距离后坡上基础的承载力不受边坡的影响[11]：

λ0=(5.14/2)β

(9)

公式(8)考虑了影响承载力的各种因素，计算时需要先确定λ0，而用公式(9)计算会偏于安全，即坡角较大时得到的临界距离过小。例如，当β=45°=π/4时，计算得到的λ0=1.43。而数值计算结果表明，β=45°时，λ=3的情况下承载力仍然受到斜坡的影响。

在Georgiadis研究的基础上[12]可推导出黏性土坡上承载力系数的公式(10)[13]，但公式涉及的参数较多。

(10)

根据前面数值计算得到的结果，对公式(10)中的参数进行了适当的简化和拟合，得到了公式(11)：

(11)

(12)

使用公式(12)计算时需要注意的是，当f(λ)小于0时取0，即坡上承载力不能超过平地时的承载力。此时可得到斜坡对承载力影响的折减系数：

(13)

将公式(6)、(11)～(13)代入公式(2)，即可得到黏性土坡上裙板式条形基础的极限承载力。

为了验证公式的合理性，将公式求解的结果同数值计算的结果进行了对比。选取坡角较大、距离较近的4组情况，比较不同cu时的理论解和数值解。

从图10可以看出：当β=45°时，不论λ=1或2，理论解与数值解非常接近；当β=30°时，数值解略大于理论解，相差在10%以内。这表明，本研究建议的公式考虑的因素比较全面，可以较准确地计算黏性土坡上裙板基础的极限承载力。

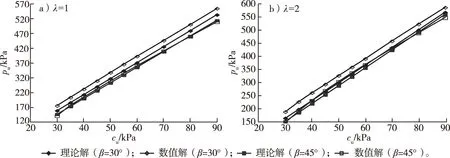
图10 理论解与数值解的结果对比(d/B=0.5)Fig.10 Comparison between theoretical and numerical results (d/B=0.5)

4 结 论

以裙板式条形基础为研究对象，采用数值计算和理论分析的方法对黏性土坡上裙板基础的极限承载力进行了研究，主要得到以下结论：

1)设置裙板可显著增加坡上基础的承载力。尤其在坡角较大时，提高幅度比较明显；且承载力随裙板相对高度增大而增大。

2)斜坡坡角对承载力有显著影响。当坡角较小时(15°)，承载力受斜坡影响不大。当坡角较大时(45°)，斜坡对承载力的不利影响逐渐增强。

3)相对距离对承载力的影响与不排水强度cu相关。当cu较低时，相对距离对承载力的影响不大；cu较高时，承载力随着相对距离的增加而逐渐提高。

4)根据数值分析结果和前人理论研究，推导了坡上裙板基础极限承载力的计算公式；通过与数值解的对比表明了公式的准确性。