欺骗攻击下一类神经网络的自适应事件触发H∞滤波

王锦霞 高金凤 谭天

0 引言

近几十年来，神经网络(Neural Networks,NNs)经过不断地发展改进，被广泛地应用在图像识别、深度学习、优化问题和信号处理等领域.而随着基于NNs的控制技术的飞速发展，滤波器作为一种具有理论意义和应用价值的控制设计引起了越来越多的研究人员的关注[1-6].文献[1] 深入地研究了基于采样数据的延迟神经网络事件触发H∞滤波；文献[3]针对单处理度量的时滞转换神经网络设计了有限时间的异步H∞弹性滤波器；文献[4]研究了一类具有马尔可夫跳跃参数和混合时滞的不确定离散随机神经网络的鲁棒H∞滤波问题；文献[6]研究了一类具有事件触发机制(Event Triggering Mechanism,ETM)和量化器的半马尔可夫跳跃离散时间神经网络模型的H∞状态估计问题.

在实际的网络通信中，由于网络的开放性、共享性、互联性和通用性，通信网络经常接收到外部的恶意攻击信号，导致系统性能严重下降，甚至可能崩溃.一般来说，网络攻击主要是指破坏信息传输系统、真实采样数据、通信基础设施和网络设备的攻击性行为.网络攻击分为三类：重复攻击、拒绝服务攻击、欺骗攻击，其中对网络安全的最大威胁是欺骗攻击[2].因此，近年来关于欺骗攻击的研究成果不断更新[2-13].文献[7]对存在虚假信息注入的网络攻击提出了基于事件触发的攻击判定机制，设计了优化的状态估计器并进行估计误差收敛性分析；文献[2,10]都研究了具有混合触发方案和欺骗攻击的神经网络模型，其中文献[2]主要研究了具有混合触发方案和欺骗攻击的神经网络的H∞滤波器设计,文献[10]则考虑到定量处理可以降低网络系统中网络传输的压力，因此在神经网络状态估计的研究中引入了量化.考虑到传统的ETM在采样数据因外部干扰而发生急速变化时，可能会触发虚假事件，文献[11]提出了一种新的ETM并设计了一种网络物理攻击系统的弹性滤波器来保证系统的安全性.这也充分说明，这种固定触发参数的方法虽然在一定程度上节省了网络通信的资源，但由于触发参数固定不变，采样数据变化差值很小时滤波系统的信息基本无法被传输利用，会导致系统的动态性能下降.因此，一种自适应事件触发通信方案出现在研究者们的视线中，这种方法能灵活地根据当前的系统误差调节触发参数，达成保持期望的动态性能和节省网络资源的最优方案.

基于以上研究成果，本文展开了基于自适应事件触发机制(Adaptive Event Triggering Mechanism,AETM)的方法对欺骗攻击影响下的NNs进行稳定性分析和H∞滤波器的设计的研究.AETM可以调整事件触发的阈值，在节省有限通信资源的同时，也能很好地保持期望的动态性能,然后建立网络攻击情况下的NNs数学模型，通过使用 Lyapunov 泛函稳定性理论给出系统渐近稳定的条件和滤波设计方案.本文最后通过一个仿真实例来验证所提出方法的有效性.

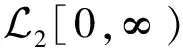
1 问题描述及系统建模

1.1 系统模型

考虑下面的一类神经网络系统模型：

(1)

1.2 自适应事件触发机制

为了减少不必要的通信资源的浪费，本文在采样器和网络通道之间引入一个事件触发器，其主要作用是根据采样数据的变化差值来判断采样信号是否需要被传输到网络通道中.参考已有的研究成果[1,14-15]，采用以下事件触发规律：

[y(k)-y(hq)]TΘ[y(k)-y(hq)]>

σyT(k)Θy(k) ,

(2)

其中Θ∈Rm是待定的正定加权矩阵，σ∈[0,1)为事件触发机制参数，y(k)是当前测量输出的采样值，y(hq)(q=1,2,…；h0=0)表示最新被传输的数据.

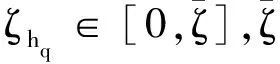
(3)

成立,且y(hq),y(hq+r)(r=1,2,…,t)满足:

[y(hq+r)-y(hq)]TΘ[y(hq+r)-y(hq)]≤

σyT(hq+r)Θy(hq+r).

(4)

定义：

(5)

对于情况1，k∈[hq+ζhq,hq+1+ζhq+1-1]，定义测量输出误差值ey(k)=0.

对于情况2，定义：

(6)

考虑到事件触发机制的不足之处,为节省网络宽带、提高系统性能，本文引入了AETM的方法.因此，定义一个变量σ(k)∈[σl,σh]，满足以下定律：

(7)

其中σl,σh分别是参数σ(k)所能允许的最小值和最大值，ε1,ε2是两个实常数，且满足ε1>1，0<ε2<1，λ是一个正常数.

注2本节采用了一种触发参数可根据当前的系统误差自动调节的方法，如(7)中所示，当前测量值和最近一次被传输的值偏差较大时(大于预设值λ)，触发参数就会变小，系统误差迅速减小，保证了系统的动态性能.反之，当两次测量值误差较小时(小于预设值λ)，此时的系统误差较小，信号传输无需太大的传输频率也能保证系统的性能，因此触发参数变大，降低传输率[5].

结合式(6)和(7),可以得到当k∈[hq+ζhq,hq+1+ζhq+1-1]时:

(8)

(9)

其中a(k)表示外部攻击者注入的欺骗攻击信号.

1.3 滤波误差模型

构建下列H∞滤波器：

(10)

其中xf(k)∈Rn为滤波的状态向量，zf(k)∈Rp为滤波器的输出，Af,Bf,Cf为适当维数的待设计的常数矩阵.

(11)

其中

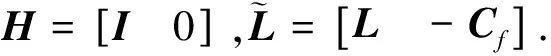
接下来，为了方便对系统(11)进行渐近稳定性分析和H∞滤波器设计，引进如下的定义、假设和引理：

假设1[11]欺骗攻击信号a(k)满足下列条件：

‖a(k)‖2≤‖Gx(k)‖2，

(12)

其中G为一个给定的常数矩阵.

假设2[17](1)中的神经函数f(.),g(.)满足初始值设置f(0)=0,g(0)=0和以下扇区有界条件：

[f(x)-f(y)-U1(x-y)]Τ[f(x)-f(y)-

U2(x-y)]≤0,

[g(x)-g(y)-V1(x-y)]Τ[g(x)-g(y)-

V2(x-y)]≤0.

(13)

引理1(Jenson不等式)[18]给定一个半正定对称矩阵M∈Rn，标量γ1,γ2(γ2>γ1),向量函数ω(i):{γ1,γ1+1,…,γ2}→Rn,如果使得如下式子是有定义的，则有如下不等式成立：

(14)

引理2[19]对于任意实数ε∈R，适维矩阵W>0,X∈Rn，下列不等式成立：

-XΤW-1X≤ε2W-2εX.

(15)

2 主要结论

2.1 H∞性能分析

下面利用李雅普诺夫函数来分析系统(11)的稳定性.

定理1给定参数ηm,ηM,ζM,σh,γ和矩阵G，若存在具有适当维数的矩阵P>0,Ws>0,Zs>0(s=1,2,3)，Θ>0和常数α1>0,α2>0满足如下线性矩阵不等式：

(16)

其中:

Ξ3=diag{-P，-Z1，-Z2，-Z3,-I},

Ξ13=diag{-α1I，-α2I，-Θ，-I,-γ2I}，

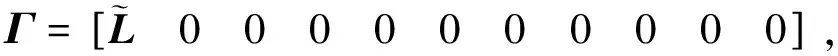
Λ2=-W1-Z1-Z2,

Λ6=-W3-Z3,

那么，基于事件触发机制(2)的滤波误差系统 (11)渐近稳定.

证明针对系统(11),选取如下Lyapunov-Krasovskii 泛函：

V(k)=V1(k)+V2(k)+V3(k),

(17)

其中：

V1(k)=xΤ(k)Px(k),

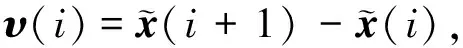
则有：

E{ΔV3(k)}=E{(ηM-ηm)2υΤ(k)Z1υ(k)+

定义：

可以得到：

(18)

根据Schur补定理，可以得到：当 (16)成立时系统(11)渐近稳定.证明完毕.

2.2 H∞滤波器设计

(19)

其中

如果 (19)有可行解，那么滤波器的参数为

(20)

证明定义以下矩阵：

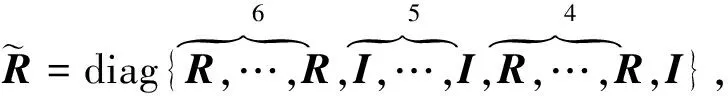
(21)

3 仿真实例

本节将通过一个仿真实例来验证结论的可行性.

将第2节的定理应用到多个水库的配水管网的监测问题中，如文献[20]中配水管网模型(图1)所示，可根据不同地区的用水需求在水库之间进行调节.水库i的蓄水和水流动力学如下：

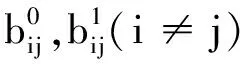
定义x(k)=[x1(k),x2(k),x3(k)]，可得到下面的系统模型：

x(k+1)=Ax(k)+B0f(x(k))+

B1g(x(k-η(k)))+Dω(k),

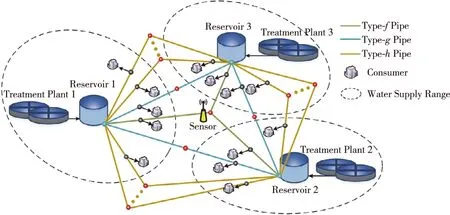
图1 配水管网结构[20]Fig.1 Framework of water distribution network[20]

其中

a1=0.339 7，a2=0.312 8，a3=0.251 3，

d11=0.170 2，d12=0.231 6，d13=0.342 4，

d21=0.274 0，d22=0.101 7，d23=0.278 9，

d31=0.106 2，d32=0.104 9，d33=0.235 5，

此外，作为反映水库间相应类型管道输水饱和度的非线性函数为

满足假设2的相关参数矩阵为

外部干扰信号为

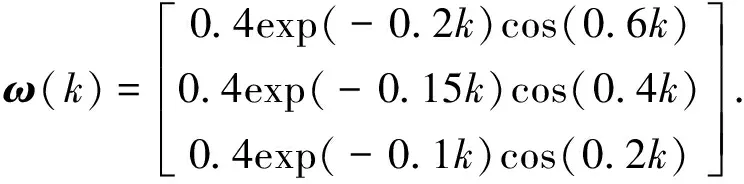
设定初始信号为x(0)=[1,2,-3]，xf(0)=[-1,1,0.5]，时滞ηm=1,ηM=4,ζM=1，

自适应参数为ε1=2,ε2=0.005,λ=2.5×10-5，初始事件触发参数为σ(0)=0,σl=0,σh=0.1，H∞性能指标为γ=3，基于第2节所给的定理及Matlab的LMI工具箱，可以得到满足条件的滤波器参数：

Θ=8.387 5.

此时，系统的待估输出响应z(k)和滤波器输出响应zf(k)曲线及其误差分别如图2、图3所示,可以看出系统处于稳定状态.图4为事件触发参数的调整情况，由于误差ey(k)起初较大，触发参数迅速减小，并且随着ey(k)的减小而增大，最后到达最大值.信号释放瞬间和释放间隔如图5所示，采样时间段内信号释放次数为39，相比设定固定事件触发参数情况下的61次触发，可以明显地看出自适应事件触发机制提高了网络资源的利用率.

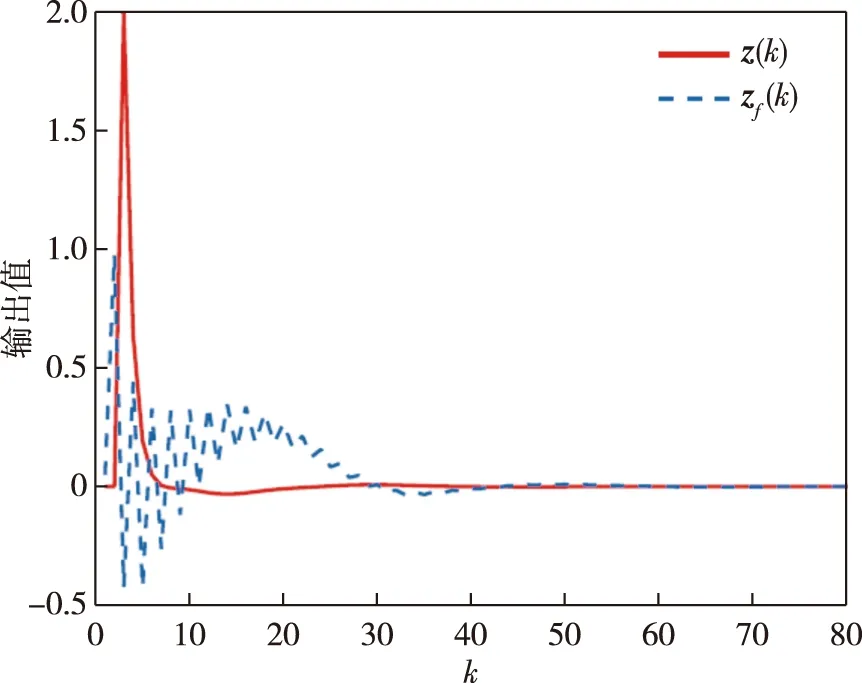
图2 待估计输出响应z(k)和滤波器输出响应zf(k)Fig.2 Responses of z(k) and zf(k)

图3 滤波误差

图4 自适应触发参数σ(k)Fig.4 Adaptive triggering parameter σ(k)

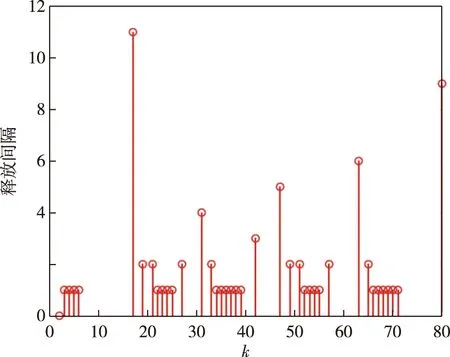
图5 事件触发图Fig.5 Release instants and their intervals

4 结论

本文针对一类遭受外部网络攻击的离散时间神经网络系统，给出了系统的渐近稳定前提下的H∞滤波设计方案.为了能更加贴近真实的网络交流环境，设定了一个遭受到外部恶意的网络攻击且带宽有限的共享通信网络，面对网络系统冗杂的数据，提出了一种自适应事件触发机制的方法，根据当前的系统误差调节触发参数，最终达到保证系统性能和节省网络资源的目的.基于所建立的滤波误差系统的数学模型，得到滤波误差系统稳定的充分条件和相应的H∞滤波器参数，并通过一个水库调配网络的实例验证了所提出的定理的有效性.在接下来的研究计划中，将会在已有研究基础上，把研究重心放在网络攻击信号的检测这一课题上.